多传感器信息融合滤袋破损检测方法
杨宏伟 熊桂龙 张松 郑金达 刘丽冰



摘要 工業环保袋式除尘器滤袋破损直接导致设备失效,目前其监测主要依靠出口浓度检测,局限性大,误检率高。基于过滤过程滤袋破损特征分析,提出了一种多传感器信息融合滤袋破损监测方法。首先,通过理论分析和实验研究,明确了滤袋破损状态下的多传感器信号特征;研究了多传感器数据融合方法,给出了基于D-S证据理论的滤袋破损监测数据融合算法和实现过程。针对大型工业袋式除尘器滤袋不同破损状态监测实验,结果表明,将多传感器数据融合技术引入滤袋破损监测中,提高了监测的可靠性与灵敏度。
关 键 词 滤袋破损监测;多传感器;信息融合;D-S证据理论
中图分类号 TQ172.688.3;X513 文献标志码 A
Bag breakage monitoring based on multi-sensor information fusion
YANG Hongwei1, XIONG Guilong2, ZHANG Song3, ZHENG Jinda3, LIU Libing1
(1. School of Mechanical Engineering, Hebei University of Technology, Tianjin 300130, China; 2. School of Resources Environmental and Chemical Engineering, Nanchang University, Nanchang, Jiangxi 330031, China; 3. Sinoma Technology & Equipment Group Co Ltd, Tianjin 300400, China)
Abstract The breakage of the bag used in industrial environmental bag filter can directly lead to equipment failure. At present, the monitoring mainly depends on the detection of the export concentration, which has a large limitation and high false detection rate. In this paper, through the analysis of the bag damage characteristics, a bag breakage monitoring method based on multi sensor information fusion is proposed. First, through theoretical analysis and experimental research, the characteristics of the multi sensor signal under the condition of filter bag breakage are clarified, researched the multi-sensor data fusion method, the date fusion algorithm and implementation process of bag damage monitoring based on D-S evidence theory were given. According to the different breakage condition monitoring experiment on the industrial baghouse, the result shows that the multi sensor data fusion technology is introduced in the bag breakage monitoring and improves the reliability and sensitivity of the monitoring.
Key words bag breakage monitoring; multi-sensors; information fusion; dempester-shafer method
0 引言
滤袋是袋式除尘器的核心部件,滤袋破损直接造成烟尘的排放浓度与排放量增加。目前,袋式除尘器滤袋破损的检测方法主要有摩擦碰撞静电法、电荷感应法、光电转换法和压差测量等4大类[1-7],这些方法大多是根据运行过程中袋式除尘器出口粉尘浓度的变化来判断滤袋的破损情况,基于这种判断标准的检测方法,误检率相对较高。
滤袋破损误检率高是多方面因素造成的,一方面,在运行过程中,袋式除尘器流场结构复杂,出口粉尘浓度、气流分布均匀性、烟气温度,过滤过程中的过滤风速、过滤阻力,清灰过程中的清灰压力、清灰频率等对滤袋破损均会产生重要影响;另一方面,滤袋破损的异常数据集比较缺乏且不大容易获得,没有充分的先验知识可供参考。因此,使用多传感器信息融合方法是至关重要的。
多源信息融合或多传感器信息融合可以提高监测的准确性和及时性;多传感器信息融合方法能够处理滤袋破损检测中数据的不确定性,提高诊断结果的可信度[8]。
在多传感器信息融合系统中,各传感器提供的信息一般是不完整、不确定、模糊的,甚至可能是相互矛盾的,即包含着大量的不确定性。在不同的数据融合方法中,D-S(Dempster-Shafer)证据理论是一种高效解决不确定问题的方法,且不依赖于先验知识,已被广泛应用于决策、模式识别和风险评估[9-11]。在上述研究的基础上,本文提出了基于多传感器信息融合的滤袋破损检测方法,由多传感器获取袋式除尘器运行中的相关信号,利用D-S证据理论强大的推理能力,可避免主观判断,以期对滤袋破损状况进行准确的判断。
1 滤袋破损机理及可检测特征量分析
滤袋破损是指袋式除尘器的滤袋经过一段时间运行后,由于滤袋老化、局部疲劳、粉尘冲击与磨損以及烟气腐蚀等原因,使滤袋局部出现穿孔、破损或撕裂等而导致粉尘跑漏的现象。袋式除尘器滤袋破损的原因,大致有4类:气流磨损、机械磨损、高温烧损以及化学损坏[12-20]。
1.1 气流磨损
气流磨损主要由2方面原因造成,一方面是气流分布不均匀,另一方面是清灰方式不合理。
气流分布不均匀:含尘气流在滤袋底部和滤袋之间流动,过高的进口风速以及不合理的进气结构,造成含尘烟气高速冲刷滤袋的局部,使滤袋局部磨损、寿命降低。
清灰方式:过高的清灰压力与频繁的清灰次数都会加速滤袋的磨损,造成破袋;脉冲喷吹压缩空气偏离滤袋中心,造成对滤袋内部单侧的冲刷,加速磨损。
1.2 机械磨损
机械磨损的原因主要有以下几点:滤袋抗磨损性弱;滤袋与滤袋、滤袋与壳体边壁间距设计不合理;花板变形;袋笼的影响。
滤袋与滤袋、滤袋与壳体边壁间距设计不合理导致滤袋磨损:滤袋与滤袋之间距离或滤袋距壳体边壁距离过小,滤袋之间或滤袋与壳体边壁碰撞摩擦导致滤袋破损。
花板变形导致滤袋磨损:花板变形,袋笼的垂直度得不到保证,造成滤袋底部搭桥、挤碰、摩擦或与箱体之间的摩擦,导致滤袋底部损坏。
袋笼的影响:袋笼存在结构缺陷、锋利边缘或接口连接不当;袋笼与滤袋尺寸不匹配;袋笼防腐处理不良;袋笼的纵筋数量、支撑环之间的间距等细节的设计参数都会影响滤袋的使用寿命。
1.3 高温损坏
高温损坏的主要原因有:存在明火;烟气温度过高,超过滤袋允许的最大极限温度;滤袋不耐高温;温度监控仪表失效。
1.4 化学损坏
主要原因有:滤袋的耐酸碱性弱;烟气含酸碱性物质;烟气温度低于露点造成结露,腐蚀滤袋及壳体设备。
滤袋一旦发生较大程度的破损,大量的含尘烟气通过破口进入净气室,排放到大气中,因而袋式除尘器出口粉尘浓度会显著增加;滤袋破口位置也会因为气流的流通,造成袋式除尘器滤袋内外压差的变化;同时破损滤袋的孔洞容易形成烟气走廊,加快相邻滤袋的磨损。
综合上述滤袋破损的原因及滤袋破损后带来的工况参数变化,总结出可供滤袋破损监测使用的特征指标有出口粉尘浓度、花板上下压差、滤袋内外压差、压力损失、清灰压力、过滤风速、过滤阻力、烟气温度等。
2 滤袋破损的多传感器信息融合检测方法及其原理
多传感器信息融合是把在不同位置的多个同类或不同类传感器所提供的局部环境的不完整信息加以综合,消除传感器间可能存在的冗余和矛盾的信息,加以互补,降低不确定性,以形成对系统环境相对一致的感知描述。从而提高智能系统决策、规划、反应的快速性和准确性,降低决策风险。
2.1 滤袋破损检测系统
多传感器信息融合的结构按照信息抽象程度,可以分为3个级别,即像素级融合(也叫数据级融合),特征级融合以及决策级融合。针对袋式除尘器滤袋破损监测,不同的监测指标由不同种类的传感器采集而来,数据级融合面向同质传感器,而特征级融合和决策级融合可融合异质传感器数据。决策级融合将各个传感器获得的信号通过预处理,得出局部单一的判决,然后将所有局部判决整体分析融合,得到最终结果。决策级融合的的优点在于数据传输量较小、系统灵活性好,在非同步信息的处理上有较大优势。
决策级融合结构的数据融合算法有贝叶斯估计法,D-S证据推理法,专家系统,神经网络法,模糊集理论,可靠性理论以及逻辑模板法等。在这些数据融合算法中,D-S证据理论是通过合并多重证据做出决策,对推理进行合理的信息论解释,其重要特点是可以基于不完全的信息、证据,乃至相互冲突的证据,完成相应的推理或决策。相比于其他算法,D-S证据理论在不清楚、不确定问题上的应用有着很大优势,计算量小且不依赖于先验知识,在异常训练数据集难以获取的情况下,可以使用D-S证据理论[21]。
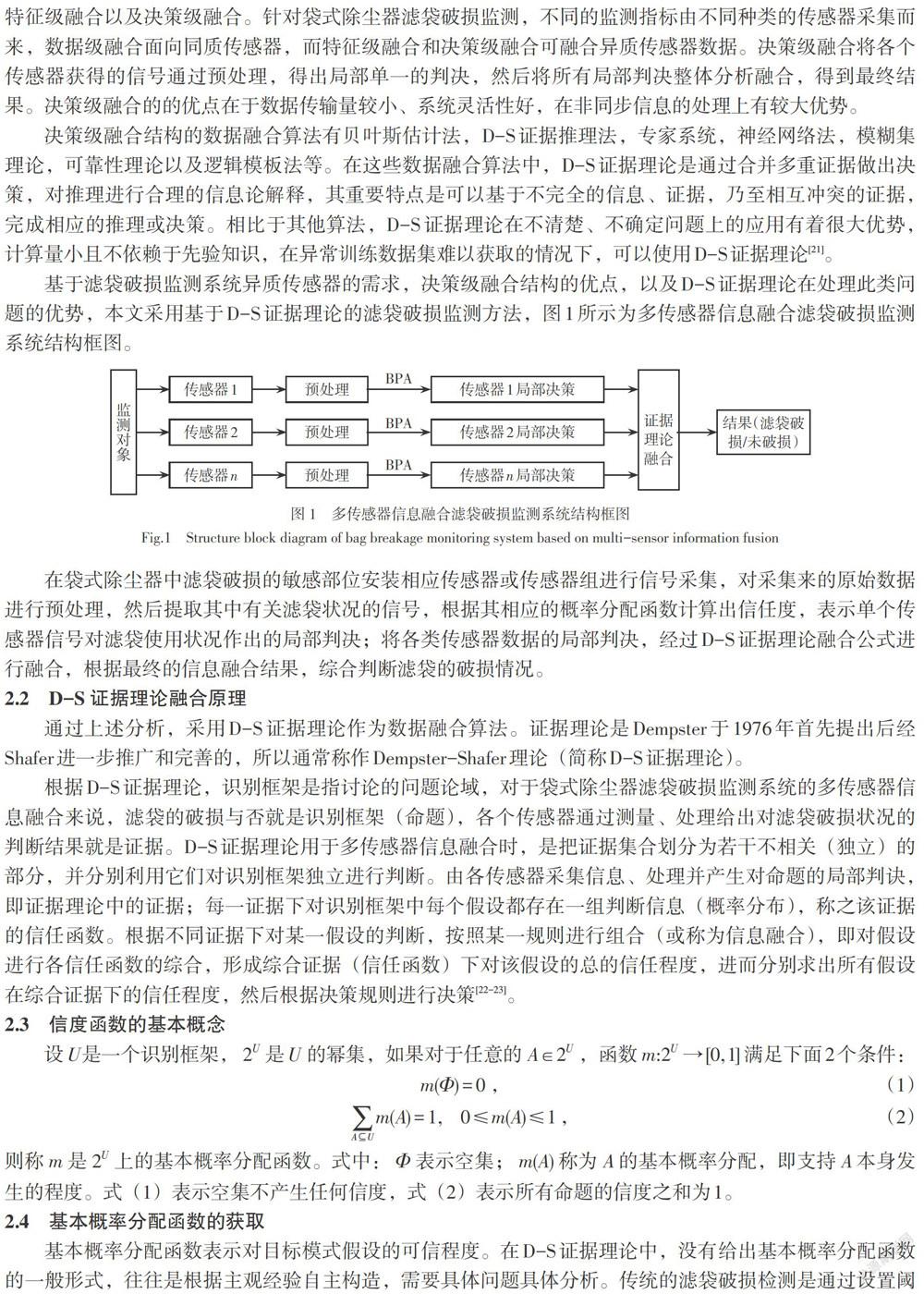
基于滤袋破损监测系统异质传感器的需求,决策级融合结构的优点,以及D-S证据理论在处理此类问题的优势,本文采用基于D-S证据理论的滤袋破损监测方法,图1所示为多传感器信息融合滤袋破损监测系统结构框图。
在袋式除尘器中滤袋破损的敏感部位安装相应传感器或传感器组进行信号采集,对采集来的原始数据进行预处理,然后提取其中有关滤袋状况的信号,根据其相应的概率分配函数计算出信任度,表示单个传感器信号对滤袋使用状况作出的局部判决;将各类传感器数据的局部判决,经过D-S证据理论融合公式进行融合,根据最终的信息融合结果,综合判断滤袋的破损情况。
2.2 D-S证据理论融合原理
通过上述分析,采用D-S证据理论作为数据融合算法。证据理论是Dempster于1976年首先提出后经Shafer进一步推广和完善的,所以通常称作Dempster-Shafer理论(简称D-S证据理论)。
根据D-S证据理论,识别框架是指讨论的问题论域,对于袋式除尘器滤袋破损监测系统的多传感器信息融合来说,滤袋的破损与否就是识别框架(命题),各个传感器通过测量、处理给出对滤袋破损状况的判断结果就是证据。D-S证据理论用于多传感器信息融合时,是把证据集合划分为若干不相关(独立)的部分,并分别利用它们对识别框架独立进行判断。由各传感器采集信息、处理并产生对命题的局部判诀,即证据理论中的证据;每一证据下对识别框架中每个假设都存在一组判断信息(概率分布),称之该证据的信任函数。根据不同证据下对某一假设的判断,按照某一规则进行组合(或称为信息融合),即对假设进行各信任函数的综合,形成综合证据(信任函数)下对该假设的总的信任程度,进而分别求出所有假设在综合证据下的信任程度,然后根据决策规则进行决策[22-23]。
2.3 信度函数的基本概念
设U是一个识别框架,[2U]是[U]的幂集,如果对于任意的[A∈2U],函数[m:2U→[0,1]]满足下面2个条件:
[m(Φ)=0], (1)
[A?Um(A)=1,0≤m(A)≤1], (2)
则称[m]是[2U]上的基本概率分配函数。式中:[Φ]表示空集;[m(A)]称为[A]的基本概率分配,即支持[A]本身发生的程度。式(1)表示空集不产生任何信度,式(2)表示所有命题的信度之和为1。
2.4 基本概率分配函数的获取
基本概率分配函数表示对目标模式假设的可信程度。在D-S证据理论中,没有给出基本概率分配函数的一般形式,往往是根据主观经验自主构造,需要具体问题具体分析。传统的滤袋破损检测是通过设置阈值,根据传感器采集数据是否超过阈值来判断滤袋的破损,这样造成滤袋破损的概率只能是1或者0,检测结果片面化和绝对化。而模糊集合将普通集合里的隶属关系灵活化,把原来只能取0/1的值扩充到可以取0到1之间的任意数值,并且通过选取适当的模糊隶属度函数,在滤袋破损检测中还能最大化保留检测不确定性的概率。隶属度函数主要由传感器本身的工作特性以及被测特征指标的特性而确定,本文根据滤袋破损监测指标的特点和专家知识,构造了滤袋破损监测的隶属度函数,作为其基本概率分配函数。以文中提到的粉尘浓度传感器为例,当袋式除尘器滤袋完好,工作环境正常且稳定时,出口粉尘浓度会在一定范围内([T0~T1])波动,此时可认为滤袋破损概率基本为0,滤袋处于完好状态;当出口粉尘浓度逐渐升高,滤袋出现破损的概率也逐渐增加,反之,滤袋完好的概率在逐渐下降,如图2中([T1~T2])区间;当粉尘浓度超过某一阈值时([T2~T∞]),则可认为滤袋出现破损。因此,定义基本概率分配函数如下:
式中:[k=1,2,...,N],为传感器的数量;[mk1]为传感器对应的滤袋破损的概率分配;[mk2]为传感器对应的滤袋完好无损概率分配;[mk3]代表不确定的概率分配;[Rk]为该传感器的可靠度。图2表示粉尘浓度传感器采集信号对滤袋破损状况的基本概率赋值图。
根据实际实验数据分析,或通过相关文献以及专家提出的经验值,给出对应传感器的边界条件[T0]、[T1]、[T2],以及传感器本身的可靠度,根据式(3)~(5),即可计算得出各传感器采集信号所对应的基本概率分配函数。
2.5 D-S证据组合规则
根据D-S证据理论的Dempster合成法则,2个不同证据的组合方法为
[m1⊕m2(A)=0A=Φ11-KB?C=Am1(B)?m2(C) A≠Φ], (6)
其中,[K]为不同证据源冲突程度的归一化常数:
[K=B?C=Φm1(B)?m2(C)]。 (7)
[K=0]时,表示2个证据完全一致(完全相容);[0<K<1]时,表示2个证据部分相同,组合方法比较有效;[K=1]时,表示2个证据完全矛盾,证据组合规则不再使用,需要对冲突证据做处理。
对于识别框架U中A的n个相互独立的基本概率分配[m1,m2,...,mn],其组合后的基本概率分配正交和[m1⊕m2⊕...⊕mn(A)]为
将各个传感器采集信号计算得到的基本概率分配函数,带入式(8)~(9)中,进行证据的组合,得出融合结果,即为综合证据下对识别框架中每个假设的信任度,进而判断滤袋是否破损。
3 实验与分析
3.1 实验设计
目前的袋式除尘器滤袋破损检测大多是根据单一的粉尘浓度判断滤袋的破损与否。本文将基于证据理论的数据融合方法引入滤袋破损检测中。通过本文第2节的分析,结合实验现场的实际条件,拟采用袋式除尘器出口粉尘浓度、滤袋内外压差与花板上下压差3个信号,从不同的角度监测滤袋的破损,再使用D-S證据理论进行信息融合,综合判断滤袋破损状况。
基于Labview設计研发了袋式除尘器测试实验平台,该实验平台基于袋式除尘技术及Labview测试控制原理,以1∶1的比例按照实际工程中使用的袋式除尘器搭建而成的单袋室实验装置,长宽约为800 mm×800 mm,高度约16 m。硬件系统包括传感检测、实验控制等;软件系统包括智能仪器组态、操作显示面板、数据采集处理、综合分析评价及显示存储等。图3所示为实验系统主界面,主要实现实验登记与参数设置,数据的显示以及实验操作等功能;图4所示为部分后面板程序。
为验证本文提出的方法的可行性与正确性,选取长度、直径、材质完全相同的完好滤袋以及事先处理过的破损滤袋分别进行对比实验。滤袋选取工程实际使用的PTFE玻纤覆膜圆柱形滤袋,其长度为10 m、直径为0.16 m。在袋式除尘器的出口处安装粉尘浓度传感器;花板上、下安装压力传感器以测量花板上下压差;滤袋内、外安装压力传感器以测量滤袋内外压差,压力传感器安装在破口附近,完好滤袋与破损滤袋的压力传感器安装位置相同。破损滤袋的处理方式如图5所示。使用单一滤袋进行多次过滤清灰实验,采集相关信号。
3.2 实验结果与分析
本文使用D-S证据理论,识别框架为[U=F1,F2,Θ],[F1]表示滤袋破损,[F2]表示滤袋完好,[Θ]表示不确定,即由于基本可信度分配误差和各种不确定因素导致不能确定是否出现破损的情况,用不确定代替。采集3组证据源[m1],[m2],[m3]分别为出口粉尘浓度,滤袋内外压差以及花板上下压差。对应于式(3)~(5)中,[m11],[m12]为出口粉尘浓度对应的滤袋破损与否的概率分配;[m21],[m22]为滤袋内外压差对应的滤袋破损与否的概率分配;[m31],[m32]为花板上下压差对应的滤袋破损与否的概率分配(由于花板上下压差与滤袋内外压差选用的压力传感器型号相同,所以计算公式也相同);[R1],[R2]分别为粉尘浓度传感器与压力传感器的可靠度。为验证方法可行性,根据前期现场实验采集到的大量实验数据,分析总结后,设定本次实验中,粉尘浓度对应的[T0=0],[T1=10],[T2=35],[mg/m3];滤袋内外压差对应的[T0=0],[T1=600],[T2=850],[Pa];花板上下压差对应的[T0=0],[T1=650],[T2=850],[Pa];[R1=R2=0.95]。因此可由式(3)~(5)计算得出各传感器采集信号的基本概率分配函数。
在相同的实验条件下(相同的实验参数与工况参数),首先使用完好滤袋进行过滤清灰实验,采集相关信号,经过处理后根据式(3)~(5)计算得出基本概率分配函数,再使用式(8)、(9)进行D-S数据融合,得到融合结果,数据如表1所示;然后更换事先处理过的带有破口的滤袋,分别打开破口1与破口2进行实验,采集相关信号,经过处理后数据及融合结果如表2、表3所示。
根据表1完好滤袋实验数据可得知,单个传感器数据判断滤袋完好的概率分别为0.85、0.91、0.87,使用D-S证据理论进行融合判断,得到滤袋完好的概率为0.997 9,结果比单一传感器更加准确;表2、表3中破损滤袋数据可得出同样的结论,如表2中单个传感器数据判断滤袋破损的概率分别为0.83、0.75、0.62,其融合后判断滤袋破损的概率为0.9703,表3中单个传感器数据判断滤袋破损的概率分别为0.91、0.82、0.74,其融合后判断滤袋破损的概率为0.994 0;对比表2、表3数据融合结果,其判断滤袋破损的概率分别为0.970 3和0.994 0,与破口2面积大于破口1面积相吻合,滤袋破损的概率也在增加;当滤袋发生破损时,与袋式除尘器出口处的粉尘浓度传感器相比,在破口附近布置的压力传感器对滤袋的破损更为敏感,检测速率也更快。
当监测系统中某一传感器发生异常,如表4所示,粉尘浓度传感器测量信号表征滤袋破损概率为0.73,而滤袋内外压差传感器及花板上下压差传感器的测量信号表征滤袋破损的概率仅为0.08与0.15。这两者相互矛盾,此时使用单一传感器判断滤袋破损可能会带来误判。分析其造成原因,例如管道中有大量灰尘,在喷吹清灰时被气流带动,导致采集到的出口粉尘浓度数据异常,而实际滤袋并未破损。使用D-S证据理论进行融合判断,得出滤袋破损的概率为0.140 7,未破损的概率为0.855 8,更加接近实际情况,提高判断的准确度。
4 结论
本文分析了袋式除尘器滤袋破损原因及现有滤袋破损检测方法的不足之处,提出了基于多传感器数据融合的袋式除尘器滤袋破损监测方法,应用D-S证据理论进行数据融合,综合各传感器信号判断滤袋破损。从研究结果可以看出,与传统的单一传感器检测方法相比,多传感器数据融合监测方法提高了监测的灵敏度与可靠性,在一些复杂工况下,可以避免因单一传感器的失效或突变数据造成的误判,对保证设备稳定高效地运行具有重要意义,同时为袋式除尘器设备的物联化、智能化的发展方向以及为袋式除尘器技术的提升奠定良好基础。
参考文献:
[1] 余新明,吴学军,吕先昌. 布袋收尘穿漏监测及定位技术现状与展望[J]. 工业安全与环保,2005,31(5):13-14.
[2] 谢志英. 静电荷法布袋除尘检漏仪的研制[J]. 微计算机信息,2005,21(12S):153-154,127.
[3] 向晓东. 一种布袋除尘器检漏仪. 中国:200910273456. 4[P]. 2010-06-16.
[4] 潘卫国,王启杰,曹绛敏,等. 用速度—差压法对送粉管道煤粉浓度测量模型的研究[J]. 仪器仪表学报,1999,20(5):461-463,496.
[5] 周志存. 滤压式布袋除尘器检漏仪. 中国:20091026164. 4[P]. 2010-11-03.
[6] 谢剑英,孙成礼. 除尘布袋穿漏检测装置. 中国:200920203397. 9[P]. 2010-07-07.
[7] 李保生,李正强,纪峰,等. 一种用于袋式除尘器的滤袋破损检测装置. 中國:201110432212. 3[P]. 2012-07-04.
[8] JIANG W,HU W W,XIE C H. A new engine fault diagnosis method based on multi-sensor data fusion[J]. Applied Sciences,2017,7(3):280.
[9] LI Z W,WEN G Q,XIE N X. An approach to fuzzy soft sets in decision making based on grey relational analysis and dempster-shafer theory of evidence[J]. Artifcial IntelligenceIn Medicine,2015,64(3):161-171.
[10] 姜洪权,高建民,梁泽明,等. 基于D-S证据理论的压射工艺模式辨识技术[J]. 计算机集成制造系统,2015,21(5):1343-1349.
[11] DUTTA P. Uncertainty modeling in risk assessment based on dempster–shafer theory of evidence with generalized fuzzy focal elements[J]. Fuzzy Information and Engineering,2015,7(1):15-30.
[12] 王丹丹,钱付平,夏勇军,等. 基于故障树分析法袋式除尘器滤袋失效的研究与应用[J]. 环境工程学报,2016,10(6):3118-3124.
[13] 王春丽,李志军,王兴. 脉冲袋式除尘器滤袋机械破损的原因及其预防措施[J]. 水泥技术,2014(3):93-94,98.
[14] 何红儿. 袋式除尘器滤袋的破损形式及预防措施[J]. 中国高新技术企业,2012(3):116-118.
[15] 柴旭昇. 袋式除尘器气流均匀性及优化的数值模拟研究[D]. 衡阳:南华大学,2015.
[16] 谷艳玲. 高温烟气袋式除尘系统关键技术研究[D]. 沈阳:沈阳工业大学,2015.
[17] 李东梅,田娱嘉,郭阳,等. 布袋除尘器滤袋使用寿命的影响因素分析[J]. 热力发电,2013,42(4):104-106.
[18] 李勇,辛龙胜. 基于Fluent的脉冲袋式除尘器内滤袋破损研究[J]. 橡塑技术与装备,2011,37(3):1-5.
[19] 杜振,钱徐悦,魏宏鸽,等. 袋式除尘器运行情况分析及延长滤袋寿命的运行措施[J]. 热力发电,2013,42(3):74-76,94.
[20] 王冠. 脉冲袋式除尘器内部流场的研究[D]. 北京:中冶集团建筑研究总院,2007.
[21] 蓝金辉,马宝华,蓝天,等. D-S证据理论数据融合方法在目标识别中的应用[J]. 清华大学学报(自然科学版),2001,41(2):53-55,59.
[22] 张冀. 基于多源信息融合的传感器故障诊断方法研究[D]. 北京:华北电力大学,2008.
[23] 何慧梅. 基于多传感器数据融合的水质异常检测方法研究[D]. 杭州:浙江大学,2013.
[责任编辑 杨 屹]

