在小学数学教学中培养学生推理能力的策略
黄苏萍


摘要:在小学数学教学中培养学生的数学推理能力,是一个非常重要的教学目标。数学推理能力的培养应贯穿于数学教学的始终,因为数学推理能力的形成和提高需要一个长期的、循序渐进的过程。教学中,我们可以通过三个策略来发展学生的数学推理能力:以“猜想验证”为载体,发掘相同属性,促类比推理能力的提升;以“巧妙转化”为桥梁,沟通知识联系,促演绎推理能力的发展;以“探求规律”为抓手,深入问题本质,促归纳推理能力的提高。
关键词:数学推理能力;类比推理能力;演绎推理能力;归纳推理能力
数学推理一般包括合情推理和演绎推理,合情推理又包括类比推理、归纳推理等合情推理。在解决数学问题的过程中,两种推理功能不同,相辅相成。
数学推理能力是《义务教育数学课程标准(2011年版)》所提出的十个“核心词”之一,《义务教育数学课程标准(2011年版)》在其教学总目标 “数学思考”部分指出:“在参与观察、实验、猜想、证明、综合实践等数学活动中,发展合情推理和演绎推理能力,清晰地表达自己的想法。对于第一学段学段(1-3年级)的学生来说,应学会在观察、操作等活动中能提出一些简单的猜想。对第二学段(4-6年级)的学生来说,要学会观察、实验、猜想、验证等活动中,发展合情推理能力,能进行有条理的思考,能比较清楚地表达自己的思考过程与结果。”可见,在小学数学教学中,培养学生的数学推理能力,是一个非常重要的教学目标。
数学推理能力的培养应贯穿于数学教学的始终,因为数学推理能力的形成和提高需要一个长期的、循序渐进的过程。培养学生的数学推理能力,是发展和培养学生创新能力的基础,也是发展学生创新能力的必要条件。同时,推理又在很大程度上推动着学生运算能力和空间想象能力的发展,推动着学生严谨科学的学习态度的养成。
一、以“猜想验证”为载体,发掘相同属性,促进类比推理能力的提升
类比推理是根据两个或两类对象有部分属性相同,从而推出它们的其他属性也相同的推理,简称类推。类比推理的前提是需要两个或两类对象有部分属性相同,此为类推的基础。学生进行类推的过程需要有一定的载体,这个载体就是“先猜想后验证”的学习过程。荷兰数学教育家弗赖登塔尔认为:“真正的数学家常常凭借数学的直觉思维作出各种猜想,然后加以证实。”“先猜想后验证”是科学探究的一般规律,学生在猜想“可能是什么”之后,运用各种方法进行求证判断“为什么”,从而得出结论,这个过程就是推理过程。
在教学人教版《义务教育教科书·数学》四年级下册第五单元“四边形的内角和”时,学生已经有了“三角形的内角和是180度”的基础,因此教师可以借助“猜想验证”的方式,组织学生进行类比推理,猜想四边形的内角和。在教学中,要发掘三角形内角和与四边形内角和的相同的属性,为学生的类比推理提供两方面的基础:一是知识内容的类推基础。学生已经具备了“三角形的内角和”的知识基础,而“四边形的内角和”与“三角形的内角和”之间存在着联系,都属于多边形的内角和,内角和和边数之间存在着联系,有部分屬性是相同的,为类比推理提供了条件。二是方式方法的类推基础。学生学习三角形的内角和时,学会了应用量一量、算一算、剪一剪、拼一拼等操作方法来验证三角形的内角和,这为研究四边形的内角和类比推理提供了方法支持。
在此基础上,还要为学生提供猜想的机会,让学生猜想“四边形的内角和可能是多少”,然后组织学生开展“猜想—验证—总结”的探究活动。学生从特殊的四边形(长方形和正方形)入手,了解了这些特殊的四边形有四个直角,内角和就是360°,从而猜测其它的四边形的内角和可能是360°。这样,学生自然而然地就能够将三角形内角和的验证方法进行迁移,进而开展四边形内角和是否为360°的验证活动。然后,学生对不同的四边形展开探究,通过与三角形内角和验证活动相似的“剪一剪”“拼一拼”“量一量”等操作活动,开展类比推理活动,验证无论是哪种四边形,内角和均为360度的结论。这让学生亲历了知识的形成过程,有效地发展了学生的类比推理能力。
二、以“巧妙转化”为桥梁,沟通知识联系,促进演绎推理能力的发展
演绎推理是获得新的数学结论的思维形式与方法,其实质是以一般性的公理、原理、定律和相关事实为前提,遵循一定的逻辑规则,得出个别或特殊结论的思维形式。进行正确的演绎推理,关键在于要有理有据。在小学阶段,培养学生的演绎推理能力,需要让学生能收集、选择、处理数学信息,并寻找分析出信息之间的关系,找到推理的有力依据。转化是寻找依据的重要手段,它是数学中最常用的思想,其精髓在于将未知的、陌生的、复杂的问题通过演绎转化为已知的、熟悉的、简单的问题,学生的数学学习中到处都渗透着转化的思想。
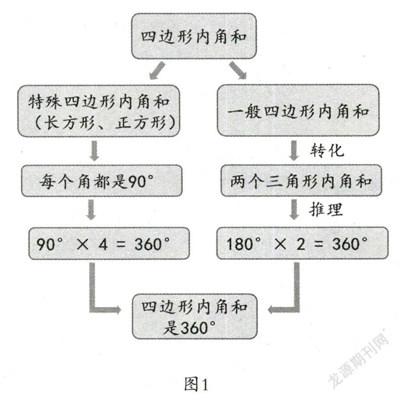
在验证四边形的内角和是360°时,缺少转化的过程,是无法推理出结论的。特殊的四边形,即长方形和正方形的内角和可以通过计算直接证明出结论。但是,一般的四边形却无法直接推理出来,这时就需要沟通“三角形内角和”与“四边形内角和”之间的联系,形成如图1的思维过程。
如图1所示,在一般四边形的内角和的验证过程中,需要利用转化,搭建起“三角形内角和”与“四边形内角和”之间的桥梁。应引导学生作辅助线,将四边形转化成已学过的三角形。因为一个四边形可以分割成两个三角形,两个三角形的内角和之和正好等于四边形的内角和,一个三角形的内角和是180度,所以四边形的内角和是180度加上180度等于360度。借助“转化”这个桥梁,学生能轻松地验证四边形的内角和是360度这一结论。这样,在更好地理解“四边形的内角和是360度”这个知识点的同时,学生的思维经历了演绎推理的过程,推理能力也得到了发展。
三、以“探求规律”为抓手,深入问题本质,促进归纳推理能力的提高
学生的学习是一个从简单到复杂、从具体到抽象、从特殊到一般的循序渐进的过程,前面学习的知识往往是后面进一步学习的基础。而归纳推理是一种由个别到一般的推理,是从认识研究个别事物到总结、概括一般性规律的推断过程。引导学生对所学的知识进行拓展和总结,也是一个提升归纳推理能力的过程。培养学生的归纳推理能力,可以深入问题本质,让学生经历探求规律的过程,以实现其思维从特殊到一般的飞跃。
在教学人教版《义务教育教科书·数学》四年级下册第五单元“四边形的内角和”一课时,我根据多边形内角和的本质内涵,设计了一个拓展练习,让学生在已经认识的三角形内角和与四边形内角和的基础上,开展拓展研究。设计了表格,将学生研究的三角形、四边形的内角和延伸到了五边形、六边形……等多边形的内角和(如表1)。
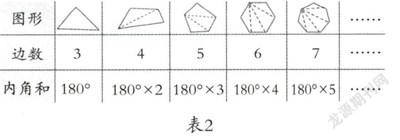
最终,学生完成表格时采用了两种方法。第一种方法如表2所示:
运用这种方法,学生思考要经历四个步骤:第一步,通过画一画,发现每个多边形都可以分割转化为若干个三角形;第二步,这些三角形的内角和之和正好等于多边形的内角和;第三步,通过观察,发现分割的三角形的个数与多边形的边数之间存在联系,即三角形的个数=多边形的边数-2;第四步,推理出多边形的内角和公式:多边形的内角和=180°×(边数-2)。第二种方法如表3所示:
运用第二种方法,学生的思考也要经历四个步骤:第一,通过画一画,发现每个多边形都可以分割转化为若干个三角形;第二,这些三角形的内角和之和,比多边形的内角和多出一个周角;第三,通过观察,发现分割的三角形的個数与多边形的边数之间存在联系,即三角形的个数等于多边形的边数;第四,推理出多边形的内角和公式:多边形的内角和=180°×边数-360°。
无论学生用以上哪种方法去思考,每种方法的四个步骤实际就是归纳推理的过程,从特殊多边形的内角和中找出规律,从而归纳出求多边形内角和的公式,实现从特殊到一般的推理过程,既能训练产生的思维,又能培养他们的归纳推理能力。
参考文献:
[1]中华人民共和国教育部.义务教育数学课程标准(2011 年版)[S].北京:北京师范大学出版社,2012.
[2]中华人民共和国教育部.普通高中数学课程标准(2017年版)[S].北京:人民教育出版社,2018.
[3]曹培英.跨越断层,走出误区:“数学课程标准”核心词的解读与实践研究[M].上海:上海教育出版社,2017.
[4]吴正宪,刘延革.发展儿童数学关键能力[M]. 北京:教育科学出版社,2017.
[5]史宁中.学科核心素养的培养与教学——以数学学科核心素养的培养为例[J].中小学管理,2017(1).
(责任编辑:杨强)

