“图形与几何”单元复习中的教学误区及解决策略

吴志健

摘要：在“图形与几何”单元复习教学中，一些教师由于受习得性思维的束缚，形成了“整理，只有‘乱忙”“‘操作，只见‘复制”“‘练习，只是‘纠缠”’的三大误区，影响着学生核心素养的提升。在整理时，要用恰当的方式来引领学生，使其增强整理意识，掌握整理方法;在操作时，要使学生在操作性思维的基础上进行必要的推理、概括，要围绕操作要点进行质疑;在练习时，要使学生在新知与旧知的联结中不断地生成智慧，要侧重于思维的挑战、良好习惯的养成、积极情感的体验。

关键词：误区;策略;整理;操作;练习

“图形与几何”是小学数学的四大内容之一，其在小学数学中的重要地位可见一斑。但是，由于其在每一册小学数学教材中，一般只安排有一个或两个独立的单元。有时，教材上还不安排“整理与练习”来进行单元复习。因此，其单元复习课的教学常常被一些教师忽视。一些教师把“图形与几何”单元复习课，上成了“只见理念，难见内容”的课，一是只强调本单元基础知识与基本技能的系统复习，二是只关注本单元数学基本活动与基本思想的专项训练，三是只重视通过自我评价来引领学生积极情感体验。显然，“数与代数”“统计与概率”的单元复习课都能如上教学。究其缘由，这是由于教师受习得性思维的束缚，形成了误区。这里，“只见理念，难见内容”，是指误读并过分拘泥于《义务教育数学课程标准（2011年版）》所强调的教学理念，不顾及具体的教学内容，从而缺乏针对性，致使整理成为“瞎忙”、操作成为“复制”、练习成为“纠缠”。

在单元复习时，对知识进行整理、归纳、综合是至关重要的。但是，整理的目的不仅仅是帮助学生完善知识结构，更需强调学生通过整理知识的活动来发展核心素养。因此，需要用恰当的方式来引领学生有条理地整理知识，增强整理意识、掌握整理方法。问题是一些教师习惯于仅盯着教参，只是引导学生胡乱地整理知识，不再追问：整理什么？谁整理？需要整理的知识有何特征？怎样整理才合理，才有效？这就造成了“整理，只有‘乱忙”’的误区，主要表现为学生“乱整理”教师“乱指导”。

首先，学生整理单元知识无关乎其核心素养的发展。它有以下三种表现：一是学生无从下手，只能照搬教材内容。二是教师拉着学生往前赶，提供了由一些细碎问题组成的所谓指导，学生不用思考就能整理完单元知识。三是教师要求学生整理自认为必须掌握，实则无需掌握的知识点。

其次，教师对学生整理知识的具体指导没有层次性。在学生整理知识之前，没有对学生提出分层的要求;在学生整理知识时，教师没有个别辅导跟进;在学生整理知识后，教师没有相应地站在不同水平的学生角度上进行评价激励;在学生小组交流时，教师没有深入到学生中间去倾听。

例如，苏教版《义务教育教科书·数学》四年级下册第一单元“平移、旋转和轴对称”一课，在其单元知识的整理过程中，有些教师如下进行教学：首先，问学生：什么是平移？什么是旋转？什么是轴对称图形？然后，引导学生回忆出平移、旋转、轴对称图形三者的描述性概念，回顾画平移图形的注意点，回顾画旋转后图形的方法，回顾画对称轴和轴对称图形另一半的要求，并适时板书。

这样的教学中，学生难以通过话语来表达清楚平移、旋转、轴对称图形三者的描述性概念，就其教学过程而言，也如同新授课上课堂总结的拼凑，如同练习课上各类习题集体讲评时小结语的堆砌，根本无法在单元复习中利用整理知识来发展学生的核心素养。其实，上面的教学可以如下进行：在学生各自通过画图独立完成对平移、旋转、轴对称图形整理的基础上，由小组长召集组员进行讨论，形成各组的观点;再由教师引导学生进行全班交流，适时提问，归纳出应当注意的点。

“图形与几何”单元复习中操作题的设计，要突出针对性、综合性和思考性，这是基于操作的有效性与合理性而言的。所谓操作，是指度量线段的长短、角的大小、画图、进行图形变换、做数学实验等。操作活动都有相应的规范与技术要素，而这些规范与技术要素往往容易被一些教师所固化，他们认为，操作就应该使用操作性思维，要利用操作性思维来提高学生的正确率。在新授课时强调操作性思维无可非议，但在复习时若还固守这种方式就会形成“操作，只见‘复制”’的误区。即教师机械地控制着学生的思维活动，强调与原来一模一样地进行操作，使学生的操作性思维替代了必要的推理与概括，从而影响了学生批判质疑精神的培养。

这种误区，通常有以下三个特点。第一，替代操作。指学优生演示操作替代其他同伴，教师演示操作替代学生，操作结果替代操作过程。第二，只是动手。指没有对操作过程的想象，没有基于以前相同操作行为而进行指向明确的判断与推理。第三，止步于新授。指复习课上学生沿用新授课上的操作程序进行“复制”练习，教师讲评时如同新授一般对操作程序进行再讲解。

例如，有一道操作题：把三角形ABc绕A点顺时针旋转90度，把小旗图绕E点逆时针旋转90度，把三角形FGH绕F逆时针旋转90度。（见图1）

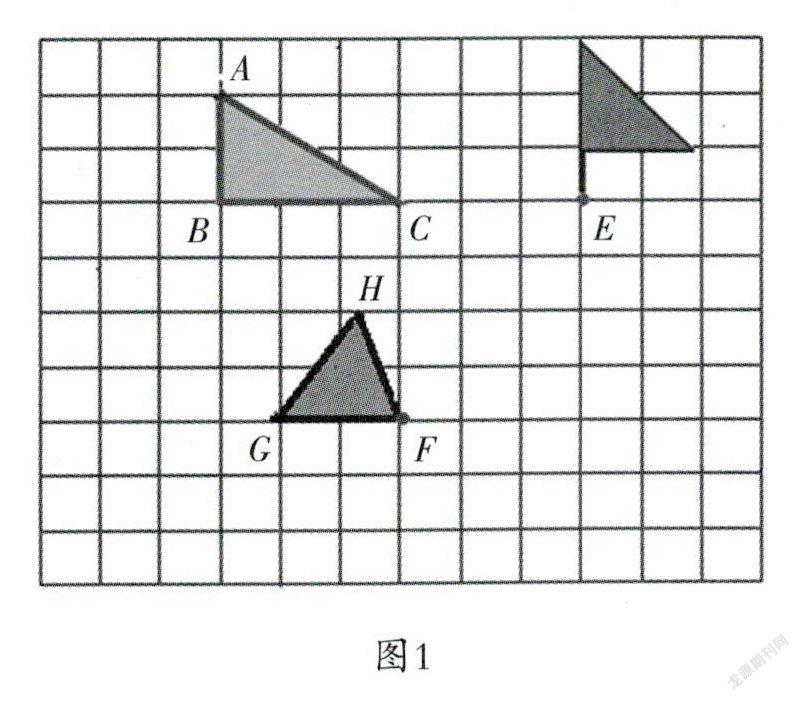
对于三角形ABC绕A点顺时针旋转90度，一些教师认为必须“复制”新授课的做法，用直角三角板分别找出AB、AC的对应边AB，AC1，（见图2）。他們引导学生如下机械地使用三角板：三角板的直角顶点与图形的旋转中心点重合，一条直角边与图形的一条边重合，按照旋转方向放好三角板，另一条直角边的位置就是对应边的位置。

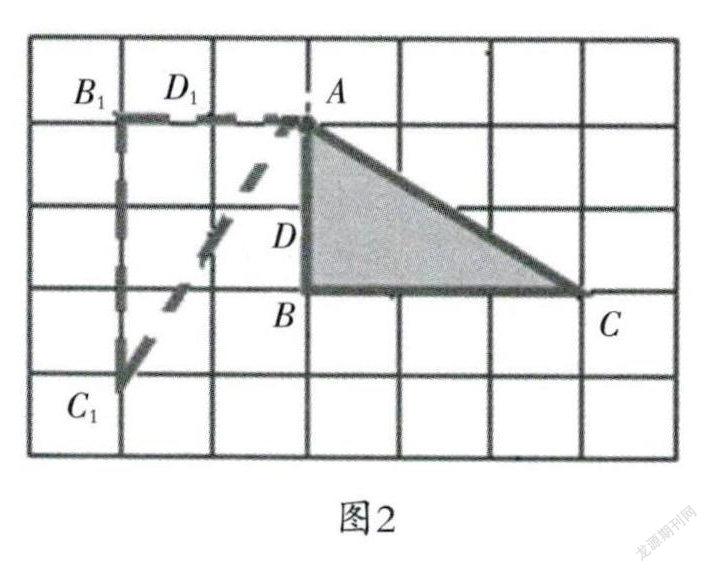
事实上，下面的方法更有效，更有利于学生形成数学学科核心素养。即运用推理方法，通过观察。而不是用手数，在方格图上找到点B的对应点B1，点C的对应点C，;或者先找到点D的对应点D，，再找到点B的对应点B1，最后找到点C的对应点C1。思维在操作中具有重要地位，这里的思维并不单指操作性思维，更指在其基础上进行的推理与概括。在各种思维活动中，要重视对应点、对应边运动轨迹的想象，引导学生围绕操作要点进行质疑，并用自己认为最合适的方式来表达，从而加深对“操作”的理解，建构认知体系，发展核心素养。

一些教师始终认为所谓练习，就是反复做题，以求熟练，尤其是在复习课上，’必须纠缠于知识点、技能与方法。这种习以为常，造成了“练习，只是‘纠缠”’的误区。

这种误区有以下三个纬度：第一，教师通过练习题帮助学生对知识进行罗列，纠缠于“新知”与做题经验，而忽视了学生对相关旧知在新情境下的应用与反思。第二，教师通过练习题帮助学生对技能框架进行建构，纠缠于书本上的结论与学生的做题速度，而忽略了学生作为主体自己对技能的思考。第三，单元复习题注重课前预设，没有课堂即时生成，忽视了学生反思习惯的养成以及主动复习意识的形成。

例如，在苏教版《义务教育教科书·数学》六年级上册的单元复习中，一位教师设计了如下思考题：一个长方形被分割成5个正方形，每个大正方形比每个小正方形多15平方厘米，每个大正方形的面积是（）平方厘米。（如图3）

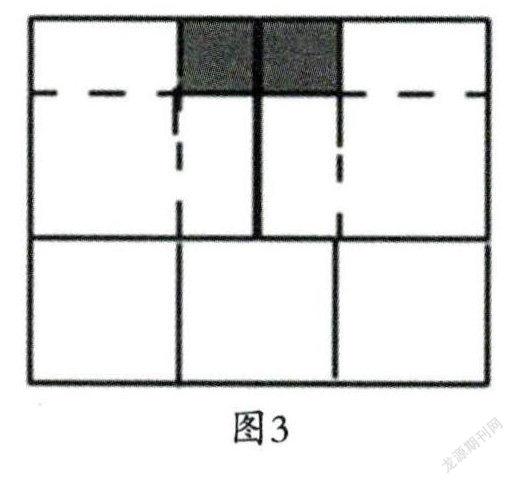
对于这道习题，他引导学生如下思考：若小正方形边长为2，则大正方形边长为3。由此可知每个小正方形面积是每个大正方形面积的4/9，再根据条件“每个大正方形比每个小正方形多15平方厘米”，就能求出每个大正方形的面积是27平方厘米。

这位教师到此就结束了教学，这样就使学生产生了解答这道题一定要使用新知（分数知识）的错觉，失去了反思运用旧知（整数知识）解答此题的机会。也就是没有充分利用新知与旧知，让学生进行反思，从而形成可以有效开发的生成性资源。

其实，本题可以用分割方法来解答（见图3）。由条件“每个大正方形比每个小正方形多15平方厘米”，可知两个大正方形的面积比两个小正方形的面积多30平方厘米。即5个同样的小长方形的面积和是30平方厘米，每个小长方形的面积是6平方厘米。也就是每個小正方形的面积是12平方厘米。由此再求出每个大正方形的面积。这里不难看出，单元复习中的练习，除了要进一步巩固所学知识与技能外，更要侧重于新旧知识在思维上的挑战，从而养成良好习惯，体验积极情感。