动态双足步行机器人混沌步态的分析与控制

【摘要】在动态双足步行机器人的大腿和小腿质量比取不同值时,分析了斜坡倾角的变化对运动状态的影响。结果表明,随着斜面倾角的增大,机器人会出现混沌步态。为了将混沌步态控制收敛到稳定步态,本文基于间歇控制和反馈控制思想,提出了间歇反馈混沌控制。既提高了能效,又使机器人保持稳定步态。
【关键词】动态双足步行机器人;混沌步态;倍周期步态;间歇反馈混沌控制
【基金资助】吉林省教育厅科学研究项目资助(JJKH20180464KJ),吉林财经大学科学研究博士基金项目(2018B13),吉林财经大学校长专项基金项目(08181934)
1. 引言
动态双足机器人的混沌步态呈现出一种毫无规律的,类似“跛行”的行走状态,有可能引起机器人的倾倒。因此对动态双足机器人混沌步态的研究既有利于挖掘人类行走的动力学原理,也利于开发和设计假肢等医疗康复设备。因而对动态双足机器人混沌步态的研究既有理论意义又有应用价值。
动态双足机器人的动力学模型是一个高维强非线性动力系统,里面包含着丰富的动力学特性。自从Gosiwami和Garcia发现双足机器人步态会出现分岔和混沌现象,众多学者开始对步行机器人的各种分岔和混沌步态展开了深入研究。刘振泽采用混沌同步控制原理设计了反向同步控制策略和脉冲控制策略,使圆规型被动行走机器人的混沌步态控制收敛到对称的周期步态。倪修华在摆动腿的足碰地后开始在髋关节施加方波力矩,通过调整控制参数使混沌步态和分岔步态控制收敛到稳定的单周期步态。虽然有许多种控制混沌步态的方法,但是应用最广泛的方法主要是基于OGY法和基于延迟反馈控制思想(DFC)。OGY法由于计算简便,控制参数的摄动量小,易于工程实现等优点,被广泛应用于双足机器人倍周期分岔与混沌步态的控制中。但由于线性化的误差,只能当机器人状态处于自身不动点小的邻域内时,才能保证控制的有效性,因此运用OGY法控制得到的吸引域比较小。为了获得较大的吸引域,DFC法也被应用到机器人混沌步态的控制中。由于DFC法一般不需要精确的系统模型,避免了目标轨道的确定,控制器结构简单,但是控制器的增益系数比较难确定。
本文将针对动态行走双足机器人研究结构参数和行走环境变化对运动状态的影响,从而实现混沌步态的分析。并结合欠驱动的特点,利用间歇作用力矩和反馈混沌控制方法,提出间歇反馈混沌控制方法,仿真实验验证了算法的有效性。
2. 双足步行机器人的三维步态的模型
本文中采用的机器人模型见图1,该机器人共有7个自由度,其中每只脚各有两个自由度,每条腿的膝关节处各有一个自由度,髋关节处有一个自由度。该机器人只在髋关节处有驱动力矩,支撑脚的侧向有被动(或主动)力。由于该机器人的驱动少于自由度个数,系统存在被动关节,因此它属于欠驱动双足步行机器人。
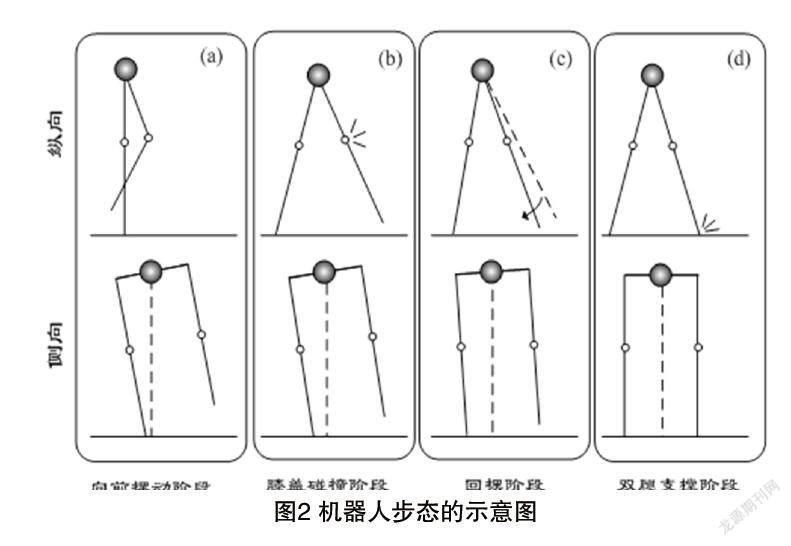
考虑的机器人带有膝关节,每个膝关节帶有锁死装置,并只在机器人的髋关节和支撑脚的侧向施加驱动控制,所有质量都是点质量。建模时忽略机器人的偏航运动,只考虑纵向和侧向的运动。因此机器人三维行走步态周期可以分解为四个阶段:①纵向:支撑腿膝关节伸直并锁死,摆动腿脱离地面,膝关节弯曲并向前摆动,侧向:支撑腿的侧向偏角从零开始,逐渐增大直到纵向质心达到最高点,接着侧向偏角开始减小;②纵向:摆动腿的大腿和小腿在膝关节处碰撞,膝关节被锁死;③纵向:摆动腿膝关节锁死后,摆动腿伸直向后回摆,侧向:侧向偏角依然在变小,相当于倒立摆的回摆;④纵向:摆动腿的脚与地面发生碰撞,支撑腿与摆动腿角色互换,侧向:侧向偏角还原为零。四个阶段中,机器人的运动具有不同的动力学特性,可以利用牛顿-拉格朗日动力学原理和角动量守恒原理建立各个阶段的动力学模型,图2展示了周期步态中各阶段的状态。
3. 双足步行机器人混沌步态的分析
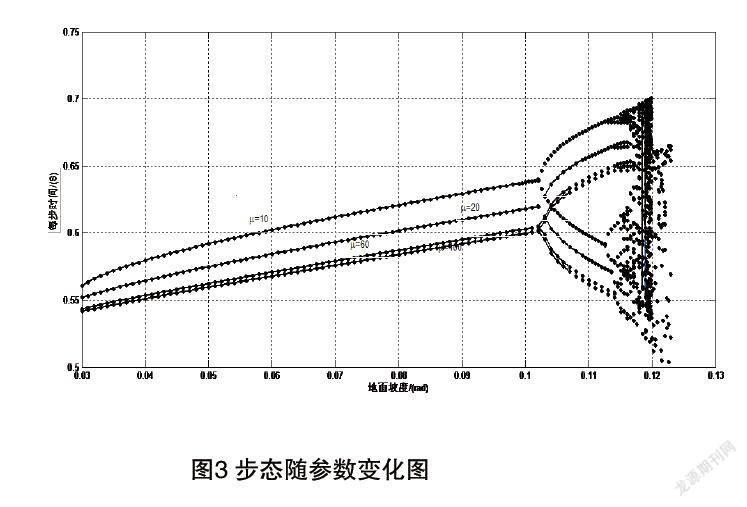
本文主要研究在机器人的行走环境和结构参数发生变化时,三维动态行走受到的影响。在结构参数中,我们将机器人大腿和小腿的质量比作为可变参数。当大腿和小腿的质量比取固定值时,令斜面倾角不断增大,观察步态的变化情况。通过仿真实验得出随着斜面倾角的增大,机器人的步态会从单周期步态变为倍周期步态,最终为混沌步态的过程,如图3所示。从图中可以看出虽然大腿和小腿的质量比相差很大,但是出现倍周期步态的坡度几乎相同。
4. 双足步行机器人的间歇反馈混沌控制
由于机器人结构参数的变化和行走环境的变化都会使机器人出现混沌步态,而混沌步态的出现往往对于机器人系统是有害的,应当加以抑制。本文研究的机器人只在髋关节施加驱动力矩,且当机器人沿斜坡向下行走时,具有重力的作用,因此结合间歇控制和反馈控制的思想,本文提出一种控制混沌步态的方法:
在机器人髋关节处安装1个可进行力矩控制的伺服电机提供动力输入,两足底部和两腿膝关节处各安装1个接触开关,用于检测机器人与地面间、机器人大腿和小腿间的接触状态。控制器将采集到的接触开关信号进行分析,然后,向伺服电机发送控制指令。当足与地的某一接触开关在某一时刻由非接触状态转变为接触状态时,表明此刻为足与地发生碰撞时刻,此时控制器记录并存储此时系统的状态,并且发送指令使伺服电机输出设定的控制力矩,其中代表当前足与地碰撞后的状态,代表上一步中足与地碰撞后的状态。当某个膝关节的接触开关在某一时刻由非接触状态转变为接触状态时,说明摆动腿的膝关节琐死,此后伺服电机停止工作,机器人在惯性的作用下继续运动直至摆动腿与地面发生碰撞为止。碰撞发生后,机器人将周期性地重复前面的步行模式。
5. 结论
本文利用数值模拟实验,分析了机器人结构参数变化和行走环境变化对步态的影响。结果表明,当大腿和小腿的质量比作为可变参数时,随着斜面倾角不断增大,机器人会出现倍周期步态,混沌步态。当机器人沿斜坡向下行走时,摆动腿膝关节碰撞前在髋关节作用反馈常值力矩,膝关节碰撞后间歇力矩作用,利用惯性向下行走,从而既节省了能耗,又将混沌步态控制收敛到稳定步态。
参考文献:
[1]S.Montazeri Moghadam、M.Sadeghi Talarposhti、A.Niaty、F.Towhidkhah、S.Jafari、S.The simple被动动态行走的混沌模型[J].非线性动力学,2018,93(3):1183-1199.
[2]Z.Z.Liu,Y.T.Tian,C.J.Zhou.类指南针两足动物的受控反相位同步[C].
中国昆明IEEE机器人与仿生学国际会议论文集,2006年:755-760.
[3]倪修华.双足被动步行机器人性能分析及一种动力输入方法研究[D].哈尔滨:哈尔滨工业大学,2010.
[4]H.Gritli,S.Belghith,N.Khraeif.哈雷夫.基于OGY的机器人半被动动态行走混沌控制
[5]躯干驱动的双足机器人[J].非线性动力学,2015,79(2):1363-84。
[5]吴晓光,李艳会,张天赐,刘绍维,谢平.基于能量反馈与OGY法的机器人混沌步态控制.仪器仪表报,2018,39(9):55-64.
[6]刘丽梅,田彦涛.双足机器人自适应常值驱动与传感反馈结合的仿生行走控制.控制与决策,2013,28(8):1152-1164.

