十进制反码在大数加减法计算中的应用

姜令闻

【摘 要】本文提出了十进制下反码和补码的概念，并将其应用到了大数加减法运算中，将减法和加法统一为加法，降低了大数运算程序代码的复杂性。

【关键词】反码，补码，大数加减法运算，程序设计

【中图分类号】G633.6  【文献标识码】A  【文章编号】1671-8437（2019）34-0171-03

大数指的是数据大小超过程序设计语言基本数据类型表示范围的整数，这种数据无法用程序设计語言提供的基本整数类型表示，需要编程者自己构造数据结构进行存储。由于不属于基本数据类型，因此也无法直接应用基本数据类型拥有的各种运算，需要编程者自己给出计算加、减、乘、除的相关算法，这就是所谓的大数计算。

大数计算也叫高精度计算，通常是信息竞赛学习的入门内容。对学习如何构造数据结构、通过实现手算运算过程学习“模拟”算法有着重要的启蒙意义。

大数计算所处理的数据通常具有明确的上限，因此可以用确定长度的数组表示，其中数组的每一元素用以存储大数的每一位，大数不存在的高位视同为0。由于每一元素都只用来表示0～9十个数字，且在加减法运算中的中间结果均不超过两位数，故数组元素可以设为char类型。由于整数运算要求逐位对齐，所以将大数个位存储在下标为0的元素中，以便于在实现逐位对齐，按照手算的规则编写程序。

根据初中的数学知识，在两个整数的加减法运算规则是[1]：

加法法则：（1）同号两数相加，取相同的符号，并把它们的绝对值相加;

（2）异号两数相加，取绝对值大的加数的符号，并用较大的绝对值减去较小的绝对值。

减法法则：减去一个数等于加上这个数的相反数。即a-b=a+（-b）

由此不难看出，按手算规则计算两整数加减法，需要判断两数的正负号以及绝对值大小关系。而进一步进行“减去”运算时可能又需要“借位”。

这样复杂的规则给编写程序代码带来了困难，不仅使得代码难于编写，而且程序正确性也不易得到保证。为回避这种复杂性，在涉及到大数减法时，有些书只提及较大的正整数减去一个较小的正整数的情况[2]。

减法这些令人感到棘手的问题在计算机出现后不久很快就凸显出来了。为此，人们发明了二进制数的反码制与补码制，克服了这个难题，使得加法和减法都可以统一使用相同的加法器来完成，而不是分别由加法器和减法器来完成，成功地降低了计算机运算器的复杂性[3]。

这种思想，也可以用于十进制数，把减法和加法统一为加法，从而降低大数运算程序代码的复杂性。

为此这里定义确定长度（不影响一般性文中取为L=6位）的十进制数的反码为：非负值（[0，499999]）时为该6位数本身;负值时（[-500000，-1]）为9减去该数各位数字得到的结果。定义补码为：非负值（[0，499999]）时为该6位数本身;负值时为反码加1得到的结果。如，12345的反码为012345，-12345的反码为987654。不难发现在这种码制下，6位长度能表示的数据范围为[-500000，499999]，最高位小于5时表示正值，大于等于5时表示负值。

求得负值的反码之后，再加上1就得到了其补码（正值补码仍为本身），与其他补码相加就等价于减法运算。为进一步简化程序，代码中不再求补码，而是把加上补码视为初始进位值为1的加法。如，对20613-65209， -65209的反码为934790，计算过程如图 1所示：

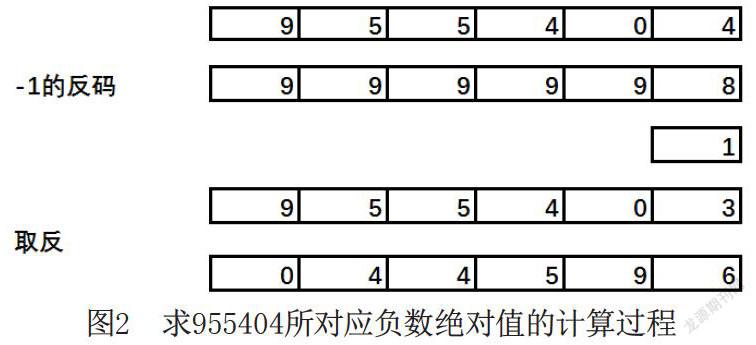
得到的955404显然是一个负值（最高位大于4），其对应的负数绝对值的求法为：减1再取反，计算过程如图 2所示：

因而，20613-65209的计算结果为-44596。

由此可见，只要增加一个简单的求负值反码的步骤，就可以将减法与加法统一为相同的过程，从而达到降低代码复杂性的目的。这种算法的正确性基于这样一个事实，对于一个负的6位整数-d5d4d3d2d1d0（其中di为一十进制数字），加上1000000后末尾6位保持不变。而

亦即减去一个正数，在被减数、减数及差都可以用6位反码制表示的前提下，加上减数反码再加1得到的结果，与减法得到的差末尾6位数字相同。

下面，以[4]的问题2为例，给出了C语言的代码实现。由于运用了反码技术，故本代码不受被减数必须比减数大的限制，甚至也不受是否有前导零的限制。

#include <stdio.h>

#define TOP （201）

#define UBD （TOP-1）

void input（char []）;

void swap（char *，char *） ;

void sub（char []，char []）;

void get_comp（char []，char []）;

void add（char []，char []，int）;

void output（char []）;

int main（void）

{

char pint1[TOP] = {0} ，

pint2[TOP] = {0} ;

input（pint1）; //输入被减数

input（pint2）; //输入减数

//相减，将差存在pint1中

sub（pint1，pint2）;

//如果pint1为负数

if （ pint1[UBD] > 4 ）

{

char tmp[TOP] = {1} ;

//为求负数绝对值先-1

sub（pint1，tmp）;

}

//输出运算结果

output（pint1）;

return 0;

}

//输出大数d

void output（char d[]）

{

//处理负数

if （ d[UBD] > 4 ）

{

putchar（‘-’）;

//对d取反求其绝对值

get_comp（d，d）;

}

int i = UBD ;

//跳过高位先导0

while （ i > 0 && d[i] == 0 ）

{

i-- ;

}

//由高到低输出

do

{

printf（“%d”，d[i]）;

}

while （ i -- > 0）;

}

//d1+d2+carry => d1

void add（char d1[]，char d2[]，int carry）

{

int i ;

for （ i = 0 ; i < TOP ; i ++ ）

{

d1[i] += d2[i] + carry;

carry = d1[i] / 10 ;

d1[i] %= 10 ;

}

}

//求d反碼=>c

void get_comp（char c[]，char d[]）

{

int i ;

for （ i = 0 ; i < TOP ; i ++ ）

{

c[i] = 9 - d[i] ;

}

}

// d1-d2 =>d1

void sub（char d1[]，char d2[]）

{

char comp_9[TOP] ;//反码

//求d2反码=>comp_9

get_comp（comp_9，d2）;

//+反码 +1

add（d1，comp_9，1）;

}

//交换p、q所执行数据的值

void swap（char * p ，char * q）

{

char t = * p ;

* p = * q ;

* q = t ;

}

//输入大数 => d

void input（char d[]）

{

int pls = 0 ;

int ch ;

//由高位到低位输入

while （ （ ch = getchar （） ） ！= ‘＼n’ ）

{

d[pls++] = ch - ‘0’ ;

}

//逆序，实现由低向高存储

int f = 0 ， b = pls - 1 ;

while （ f < b ）

{

//前后对应位交换

swap（ d + f ++ ， d + b -- ） ;

}

}

测试结果：

输入：

12345678998765432112345678988888

987654321

输出：

12345678998765432112344691334567

输入：

987654321

12345678998765432112345678988888

输出：

-12345678998765432112344691334567

表明本文在前提出的设想得到了实现，十进制反码确实可以简化大数减法的运算。此外，由于函数add（）在以0作为进位实参调用时可以完成加法运算，所以本文的程序可以很容易地扩展为大数加减法混合运算。

【参考文献】

[1]杨裕前，董林伟.七年级上册数学（第3版）[Z].南京：江苏凤凰科技出版社，2012（31）.

[2]董永建.信息学奥赛一本通（C++版）[Z].北京：科学技术文献出版社，2013.181-182.

[3]张福炎，孙志辉.大学计算机信息技术教程（2018版）[Z].南京：南京大学出版社，2018.12-13.

[4]董永建.信息学奥赛一本通（C++版）[Z].北京：科学技术文献出版社，2013.188.