水利工程土石围堰稳定性计算

蔺宏岩

（绥化学院农业与水利工程学院 黑龙江绥化 152000）

一、工程介绍

工程位于西南某江河流段，大坝为重力坝，装机容量475MW。大坝基础高程2018m，坝顶高程2110m，正常蓄水位2080m，最大坝高92m，

坝顶长500m，采用坝后式地面厂房。该水电站采用的是左岸引水隧洞导流。隧洞口围堰采用土工膜斜墙土石围堰，围堰堰顶高程2800m，最大堰高7.9m，最大挡水水头约为6.2m，堰基采用封闭式砼防渗墙，防渗墙最大深度18m，厚0.8m。引水隧洞设于库区左岸，为有压隧洞后接竖井及有压隧洞，全长约14.5km，隧洞进口底板高程2096m，开挖断面为马蹄形，出口底板高程1971m，比降2‰，引水流量120m3/s，隧洞口采用土石围堰制造干法施工环境。综合考虑现场施工进度和计划安排，临时土石围堰设计位置刚好处于距隧洞口10m 处，典型二维断面如图所示。围堰底部宽38.2m，顶部通行宽7m，南侧边坡最大斜率为1：1.5，围堰南侧联通河流，最高水位和最高低水位分别是6.2m 和4.8m，如图1-1所示。

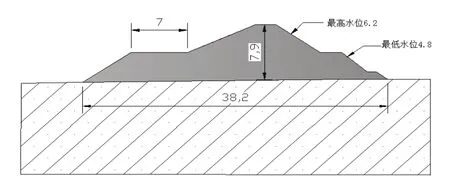
图1-1 土石围堰剖面图

二、影响土石围堰安全的因素

（一）渗流。围堰通常以临时建筑的形式出现在工程中，通常在隧洞施工导流期间给主体工程阻挡洪水而创造所需要的干燥的施工环境[1]。并且由于土石围堰具有历史悠久、能充分利用当地材料，地基适应性强，造价低，施工简便等优点而成为当今世界大多数国家临时围堰的首选。然而土石围堰失事的案例中很多是由于渗透破坏而引发的，目前世界各国均将土石围堰的渗流问题视为影响其安全的关键因素。

（二）滑坡。滑坡是土石围堰失事的另一个主要原因。滑坡是土石围堰的常见破坏现象之一，常常会给工程带来损失。我国流关岭土石围堰建设过程中出现的事故就是由于滑坡而导致的[2]。而水位的升降往往是引起滑坡的主要原因且大部分滑坡都发生于工程竣工的初期。比如，美国费琴河上的罗密尔水库建成蓄水后不到一年就发生了两起滑坡事故,其中一起发生在蓄水后半年内且也是发生在水位骤降的情况下。

（三）冲刷。围堰遭受冲刷在很大程度上与其平面布置有关，尤其在分段围堰法导流时，水流进入围堰区受到束窄，流出围堰区又突然扩大，这样就不可避免的在河底引起动水压力的重新分布，流态发生急剧改变，此时围堰的上下游转角处产生很大的局部压力差，局部流速显著增高，形成螺旋状的底层涡流速度方向自下而上，从而淘刷堰脚及基础。

（四）软基及深厚覆盖层。影响围堰安全的另一个重要因素是软基及深厚覆盖层。据不完全统计，国内外建于软基及深厚覆盖层上的水工建筑物，约有一半事故是由于建设条件复杂使得工程工期延迟而造成极大的经济损失。因为深厚覆盖层其成因类型复杂、结构和级配变化大、力学性质呈现较大的不均匀性等原因会给围堰建设带来非常大的难度。

三、土石围堰稳定性计算

（一）研究方法。

1.渗流理论。工程能否满足安全可靠和经济合理的要求，在很大程度上取决于能否正确的对工程进行正确的渗流分析和恰当的选择合理的渗流控制措施[3]。因此用一种假想水流来代替在岩石空隙运动的真实水流，这种假想水流具有通过任一断面流量与真实水流相等和在某一断面水头和压力和真实水流一样的性质。这就是渗流基本理论[4-5]。

基于饱和非饱和土体渗流的达西定律，表述如下：q=Ki

式中：q—单位体积的流量，m3/s；K—渗透系数；i—总水头梯度。

达西定律既适用于饱和土体渗流也可以应用于非饱和土渗流。唯一的区别是渗透系数在非饱和条件下的不再是常数，土体的含水量随着渗透系数变化而变化，并且水压力也间接地随着变化而变化。

达西定律经常被写成如下的形式：V=Ki

式中：V—达西流速，m/s。

实际情况下，水穿过土层的平均流速时线速度，它等于达西流速除以土的孔隙率。在非饱和土中，它等于达西流速除以单位体积的含水量。

2.有限元强度折减法原理。Midas/GTS的边坡稳定分析采用了基于有限单元法的强度折减法。有限元强度折减法的基本原理是将边坡岩土体物理力学参数（粘聚力和内摩擦角值）均除以折减率，得到一组新的Cmin、φ1，即经过折减后的抗剪强度指标为：

式中：F—边坡现状稳定安全系数；C—为滑面黏聚力；φ—滑面內摩擦角。

计算Cmin值后输出参数并进行下一步的试算，直到不收敛结束。将没有收敛的阶段视为破坏，并把未收敛阶段的最大强度折减率作为最小的安全边坡系数。当达到最小边坡系数时坡体也达到了极限状态而发生剪切破坏，同时坡体的破坏滑动面也得到。

使用Midas/GTS进行数值模拟，能够实现在非现场的情况下对真实的实际工矿做到最大限度的模拟并可以直接得到边坡的稳定系数，通过连续的的折减强度参数可以从数值上来分析坡体内塑性区域的发展情况。边坡的滑动面的形成、发育和破坏的过程可以从有限元计算结果中反映得到，从而获得边坡的最终破坏模式，同时得到边坡相应强度储备的安全系数。

（二）结果与分析。

1.渗流稳定分析。采用Midas/GTS建立有限元模型，对边坡进行渗流及稳定性计算，如表1所示。

表1 地层岩土参数取值

渗透系数取值参数选取如下：

（1）围堰南侧一层0.6m厚的不透水层，渗透系数取1.0×10e-5m/s；

（2）围堰渗透系数参照相关资料和施工经验定为1.0×10e-5m/s；

（3）基岩渗透系数取3.0×10e-5m/s。

荷载的计算包括：围堰自身自重荷载+堰身通行时过往车辆的自卸车荷载+空隙水压力。自卸车载荷：考虑自卸车满载时自重55t 最大载荷情况。自卸车后轴距1.4m，轮距1.9m。考虑土体对荷载的扩散性，填料的扩散角为39°，扩散深度按照2.0m计算得到受力面积为：

A=（2×2.0tan39o+1.4)×(2×2.0tan39o+1.9)=23.8m2

堰上不均布荷载计算值为：q=55×9.8/23.8=22.6kPa

荷载系数取1.6，则荷载设计值为：

Q=22.6×1×1.6=36.2kN/m

作用范围为：

L=2×2.0tan39o+1.9=5.12m

围堰南侧放水北侧无水，该工况只验算围堰北侧的边坡稳定性，荷载为围堰的自重荷载+自卸车荷载围堰+两侧水头差引起的渗流孔隙水压力。围堰边坡的南侧和北侧稳定计算结果如图3-1所示。

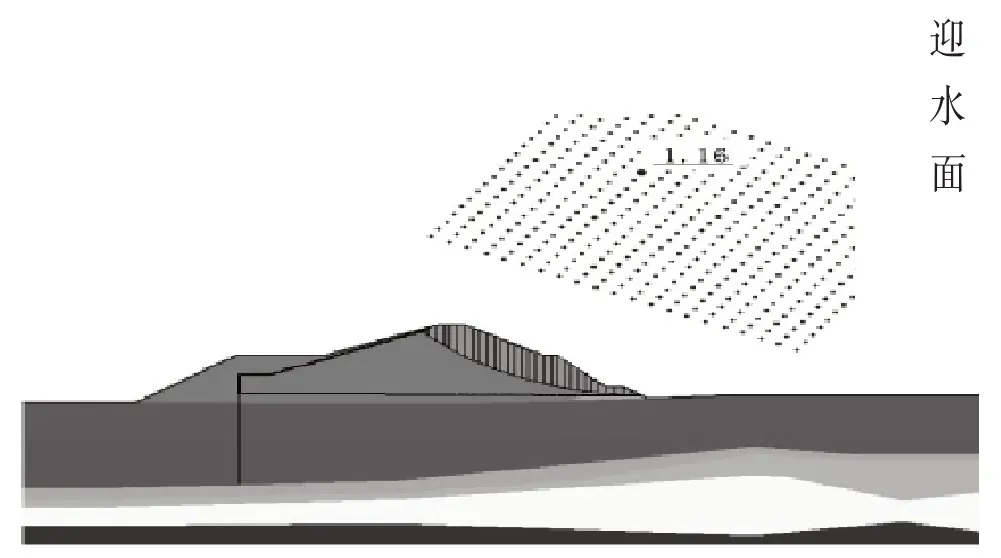
图3-1 渗流稳定分析效果图

结果表明围堰南侧有水，北侧无水。在南侧水头压力下形成稳定渗流场，并由渗流分析得北侧坡脚处渗透流量为12.4m3/d·m。将渗流计算出来的孔隙水应力场读入边坡稳定的应力场进行耦合计算，得到围堰北侧北侧的边坡安全系数最小值为1.16。

2.边坡稳定性分析。该边坡为人工回填料边坡，坡高取20m，粘聚力取20kPa，内摩擦角取39°，泊松比取0.2，弹性模量取3000kPa，渗透系数取0.001m/d。工况一： 在右侧边界施加6.2m的水头荷载；工况二：在右侧边界施加4.8m的水头荷载。通过计算得到最小水头荷载、最大水头荷载时的安全系数和滑动面位置，如图3-2所示。

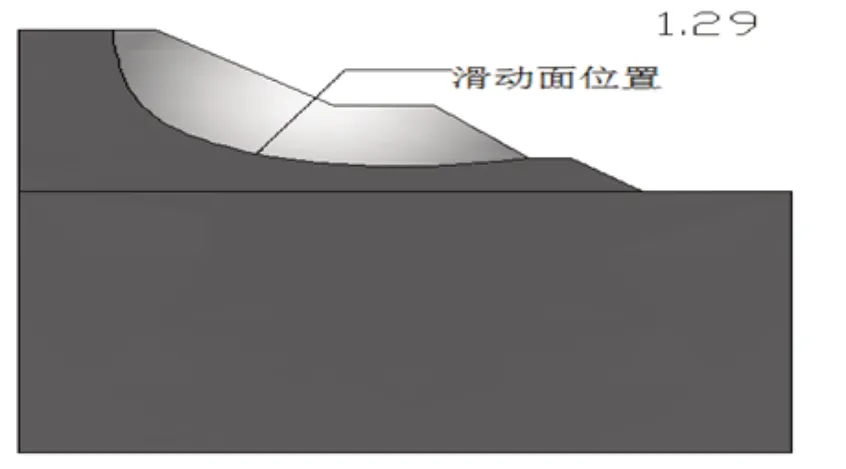
图3-2（a）最小水头荷载时安全系数和滑动位置

图3-2(b) 最大水头荷载时安全系数和滑动位置

分析可知最小水头荷载的边坡安全系数为1.29，边坡处于稳定的状态。最大水头荷载时的边坡安全系数为1.16，安全系数有所减小，边坡仍处于稳定状态，但对某些安全系数要求较高临时工程也需对边坡进行加固。基于Midas/GTS软件的计算和分析：该土石围堰在该渗流状况下是基本稳定的，发送渗流破坏可能性较小。因为由分析图示数据可知临时围堰设计断面在不少于90%密实度分层碾压施工工艺的控制下，边坡的最小安全系数为1.16，可以满足规范安全性要求。

四、结论

基于Midas/GTS软件分析计算结果得出：1.该工程围堰北侧坡脚在水压力作用下，最大渗透流量为12.4m3/d·m，渗水量较小，临时围堰设计断面在不少于90%密实度分层碾压施工工艺的控制下，边坡最小安全系数为1.16，可以满足规范安全性要求。2.为避免渗流对围堰坡脚造成影响，可在南侧距离围堰坡脚4m以外的位置开挖0.8m深的排水沟。由数值模拟的结果可以看出，围堰的潜在失稳区位于围堰南侧的浅中层围堰体内，破坏模式为弧面型滑移，沿围堰南侧滑出。