小子样成败型产品可靠性评估方法研究

周芳，王薇，陈志军，张涛

（北京强度环境研究所，北京 100076）

当“一种产品的工作特点为每件产品进行一次试验并检测，若各项性能参数均满足指标则记为一次成功，反之，则记为失败，各次试验彼此独立”时[1]，我们将这种产品称为成败型产品。如果针对一种“结构简单价格低廉”的成败型产品开展可靠度评估工作，则可投入充足的试验子样数，采用“二项分布评估法”评估即可获得产品的可靠度评估值。然而在工程实践中，大部分符合成败特征的产品，却同时集“结构复杂价格昂贵可靠性指标高”等特点于一身，导致其可获取的试验数据呈现“小子样特性”，也使得如二项分布估计可靠度评估的计数评估方法难以获得满意结果。为了解决以上存在的问题，文中系统地提出了一种基于小子样产品试验特征量的可靠性评估方法。

1 评估方法选择

成败型产品可靠性的评估可以以“计数评估”或“计量评估”[2]两种方式开展。如以“计数型”可靠性评估方法开展，其评估公式为：

式中：LR 为产品可靠性置信下限；γ 为置信度；n 为试验次数。

假设某产品的发射可靠度最低可接受值为LR =0.999，规定值为R规定=0.9995，在置信度γ =80%的情况下。根据式（1），采取计数评估方式则可获得以下结论：

1）当子样数n=1608，且无失效数据时，该产品在置信度γ =80%的情况下的发射可靠度最低可接受值 RL=0.999；

2）当子样数n=3218，且无失效数据时，该产品在置信度γ =80%的情况下的发射可靠度最低可接受值 RL=0.9995。

由计算结果可知，采取“计数型”可靠性评估方法，开展可靠性评估时，需要投入大量的试验子样，伴随而来的是巨额的产品生产经费试验经费和时间的投入，在实际工程操作中是难以实现的[3]。此种情况下，“计数型”可靠性评估方法不具有工程实践操作性。需求基于产品的性能指标特征量数据，以“计量型”的评估方法开展可靠性评估。

2 评估数据处理

2.1 评估数据的确定

为保证评估结果的有效性，评估所选取的特征量数据要与评估对象相匹配。以贮运发射筒为例，贮运发射筒是导弹武器系统的重要设备之一，它的主要任务是实现贮存支承运输和发射导弹等多种功能[4]，相应的其可靠性指标同时具有贮存可靠性指标和发射可靠性指标两项。通常情况下，发射阶段的可靠性被定义为：在规定的发射条件下，进入发射流程的动作不可以再逆转的情况下，使导弹达到预定状态的概率。在评估过程中，必须选取可说明可评价的此项特性量的飞行试验数据，以供发射可靠性评估使用。

2.2 试验数据概率分布检验

通常情况下，飞行试验中获取的试验数据，具有一定的波动性和规律性[5]。在数据获取过程中，即使操作者设备测试手段测试环境等条件相同，但获取的飞行试验数据的性能特性数据却并不完全相同，总是存在着差异，这就是试验数据的波动性。这种波动状态可被分为异常波动和正常波动。当试验数据的获取过程处于统计控制状态时，其波动服从一定的分布规律。若异常波动出现，则对试验数据质量特性值的影响较大[6]，应用此类数据开展可靠性评估，可能导致评估结果的不正确。因此，在开始可靠性评估前，必须对选取的飞行试验特征量数据开展概率分布检验和数据一致性检验[7]。

检验采用Anderson-Darling 拟合优度检验方法。Anderson-Darling 拟合优度检验是一种检验所收集的数据是否服从某个分布（如正态分布指数分布威布尔分布等）的一种方法。其原理是将所收集的数据从小到大排列，得出经验累积分布（ECDF），并与目标分布的理论累积分布（CDF）进行比较，得出AD*统计量。其值越小，数据的分布就越趋近于目标分布；其值越大，则数据服从目标分布的可能性就越小。具体的判据就是根据AD*统计量的分布计算出p 值，如果p 值大于0.05，则数据服从目标分布；如果p 值小于0.05，则数据不服从目标分布。

2.3 数据离群值的判定

针对选取的飞行试验特性量数据开展统计处理，以判断数据样本中是否存在离群值[8]。如检出离群值，确定产生离群值的原因，剔除离群值，使用剩余数据样本开展发射可靠性评估[9]。使用式（2）和式（3）计算统计数据的样本均值和标准差。

样本量均值的计算公式为：

式中：

X 为样本观测值的算术平均； Xi为第i个样本的观测值；n 为试验次数。

样本标准差计算公式为：

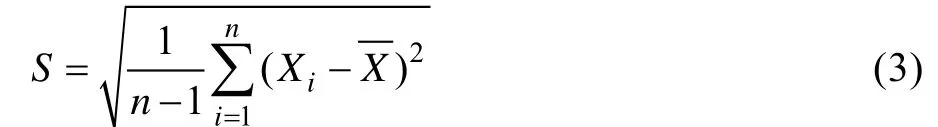
数据的检验方法有奈尔（Nair）检验法格拉布斯（Grubbs）检测法和狄克逊（Dixon）检验法。当子样数较小时，格拉布斯（Grubbs）检测法具有判定离群值的功效最优性。推荐使用该方法开展数据检验。首先，确定格拉布斯上下统计量，即nG 和nG′，格拉布斯（Grubbs）上下侧情形统计量的计算公式：

3 可靠性评估

时，判定最大值 x(n)为离群值；当，且 ( )n时，判定最小值x(1)为离群值。

根据样本统计值nX S ，参考GJB 376《火工品可靠性评估方法》中的规定，使用统计方法计算产品可靠度。由已知的产品特征量的容许上限LU下限LL按照式（6）或式（7）计算正态容许限系数KU或KL[10]。

式中：LU为性能参数上限；LL为性能参数下限；KUKL分别为用LULL计算的正态容许限K 系数；S为样本观测值的标准差；为样本观测值的算术平均。

根据计算得到的KU和KL值，查GJB 376—87 中附录C 分别确定飞行试验数据容许上限LU和下限LL的可靠度RU和RL。然后按照式（8），计算得到可靠度R。

4 案例分析

某型号产品贮运发射筒以发射过程中的产品出筒速度作为其发射可靠性评价的特性指标值，通过10 次飞行试验，获得了相应试验数据，见表1。

表1 历次飞行试验数据

4.1 飞行试验数据概率分布检验

采用Anderson-Darling 检验方法，分别针对出筒速度飞行试验数据开展正态分布指数分布威布尔分布的拟合优度检验，确认数据的概率密度分布特性。检验结果如图1 所示。经检验，不同概率分布的AD 值和p 值见表2。

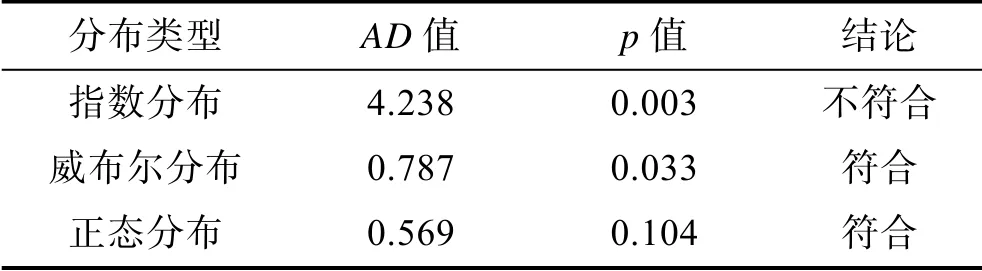
表2 飞行试验数据的Anderson-Darling拟合优度检验结果

由表2 可知，对10 次飞行试验中所获取的试验数据进行拟合分析，AD 值计算结果显示，其分布特性同时符合威布尔分布和正态分布，但从p 值判定，其符合正态分布。故认为飞行试验中获取的出筒速度试验数据的概率密度分布符合正态分布。

4.2 数据一致性检验及离群值的判定

使用统计方法直方图，针对10 次飞行试验数据开展数据一致性检验，确定所获取的数据，是否存在异常波动，如图2 所示。

根据直方图绘制结果可知，10 次飞行试验测试结果中，出筒速度呈现“孤岛型”分布特性。即个别飞行试验数据结果的获取过程中，由于非系统因素导致小概率时间发生，数据样本中可能存在偏离数据。使用格拉布斯（Grubbs）按照置信度90%的检测法进行数据离群值的检验。

由分析结果可知，在置信度90%的情况下，有1个飞行试验数据出现了离群现象。针对离群数据，应开展分析确认。如确认获取数据的过程中出现偏离，则剔除该组数据，使用剩余数据进行可靠度评估，反之保留原数据组开展评估。

图1 拟合优度检验（95%置信区间）

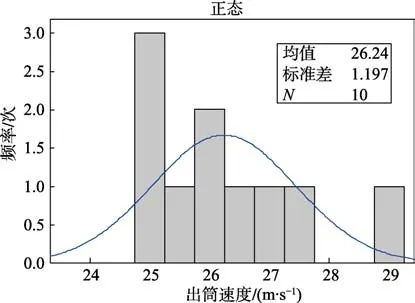
图2 飞行试验数据检验结果

4.3 可靠性评估

使用公式（6）公式（7）和公式（8），分别采用剔除状态和未剔除状态的2 组数据，开展贮运发射筒发射可靠性评估。评估结果见表4。

表4 中的计算结果显示，根据获取的10 组飞行试验数据，评估得到贮运发射筒的发射可靠度 R=0.996 32。剔除1 组离群数据后，贮运发射筒的发射可靠度R=0.999 9。评估结果说明异常波动数据对产品可靠性的评估结果影响显著，因此需要谨慎对待异常数据的剔除。

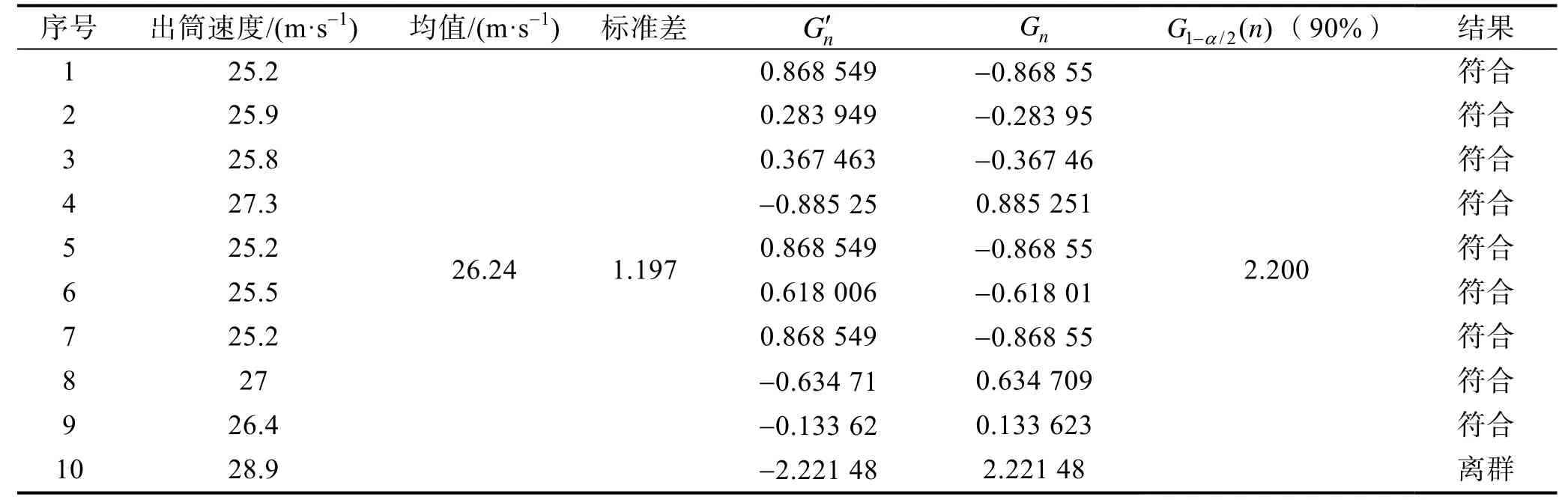
表3 飞行试验数据的格拉布斯（Grubbs）检验

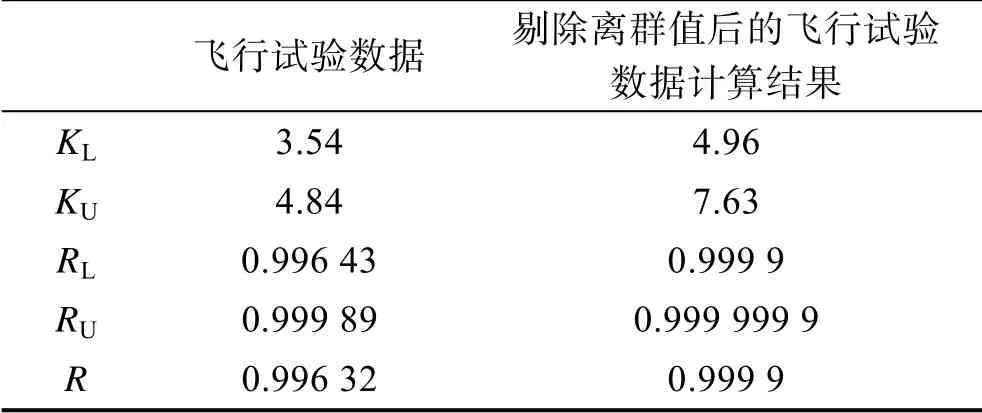
表4 可靠性单侧置信下限评估结果

5 结论

文中介绍的可靠评估方法，是一种基于小子样有效飞行试验特征量，采用计量方法对复杂结构成败型产品开展的可靠性评估方法。在评估过程中，首先要针对全部样本数据子样，开展概率分布拟合检验，确定数据分布特性，便于评估过程中选取符合相应概率分布特征的评估方法。其次，要对所有数据进行一致性检验和离群值剔除。最后使用经检验的数据完成可靠性评估，特别需要指出的是，在实际应用过程中应该尤其关注离群值的识别和剔除。事实证明，由于异常数据波动导致的分布离散性，将严重影响可靠性评估结果。当发生离群数值但无法判断获取过程异常时，可以保守地保留数据应用于评估。