沙颍河安徽段水环境容量计算及动态分析

王莹 张幼宽 梁修雨 谢显传

摘要：基于对沙颍河安徽段污染负荷的调查以及水质和流量监测数据的分析，采用MIKE11模型建立水流与水质模型，采用线性规划法，以入淮河干流Ⅲ类水为水质目标，计算沙颍河安徽段水环境容量并分析其动态特征。结果表明：沙颍河安徽段CODM。和氨氮年水环境容量分别为2.39万、0.76万t/a：受流量及上游水质影响，COD和氨氮水环境容量月变化较大，8月水环境容量最大，分别为3 557、1363 t，3月水环境容量最小，分别为621、181 t;上游水质对沙颍河安徽段水环境容量影响显著。

关键词：水环境容量;水质模型;线性规划法;沙颍河

中图分类号：X522

文献标志码：A

doi：10. 3969/j .issn. 1000- 13 79.2019.01. 018

水环境容量是指水体环境在规定的环境目标下所能容纳的污染负荷[1]。水环境容量与水体特征、水质目标及污染物特性有关，同时还与污染物的排放方式及排放的时空分布密切相关[2]，是容量总量控制的核心内容之一[3]。水环境容量计算的基本思路：通过解析或数值等方法计算河流的水流过程及污染物迁移转化规律，建立污染负荷排放与水质响应的关系，基于给定的环境目标（如水质目标）计算指定区域所能容纳的最大污染负荷。对于特定的河流，在水质目标不变的情况下，由于水文特征、自净能力和排污口排污方式的时空变异性，因此水环境容量是随时间和空间变化的。流域实际的水环境容量需要针对实际背景条件计算，即计算动态水环境容量[4]。水环境容量的计算方法主要包括公式法、模型试错法、系统最优化法（如线性规划法和随机规划法）、概率稀释模型法和模糊数学法[5-6]，其中系统最优化法适用范围广，对边界条件和设计流量的适应能力较强，是目前水环境容量计算的主流方法之一[7]。

本研究以沙颍河流域安徽段为例，采用系统最优化法中的线性规划法计算水环境容量。整体思路：根据排污数据和水功能区划确定排污口和控制断面的位置：通过河流水流和水质数值模拟，建立排污口与控制断面的水质响应关系，计算实际本底浓度值和各排污口负荷贡献度：建立线性最优化模型，计算流域水环境容量并分析其动态特征。

1 研究区概况

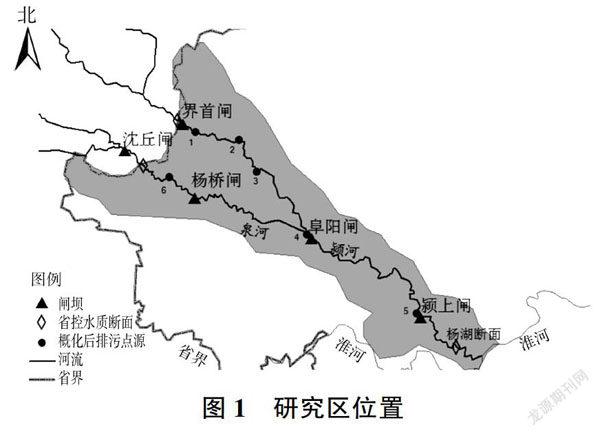
沙颍河是淮河最大的一级支流，全长624 km，流域面积39 980 km2。沙颍河流域年平均气温约15℃，年平均降水量约700 mm/a。沙颍河流域跨越河南和安徽两省，在安徽境内长208 km，流域面积4% km2，占沙颍河流域总面积的10%。沙颍河在安徽境内被称为颍河，其主要支流为汾泉河（见图1）。虽然沙颍河流域仅占淮河流域总面积的1/7，但其污染负荷排放量占淮河流域的1/3。近年来，随着工业发展和人口增长，沙颍河水质日趋恶化，污染严重，水质劣于V类的水功能区占总数的60%[8]。为控制流域水污染，实现沙颍河人淮河水质达到Ⅲ类水的目标，需要制定科学合理的污染控制方案，而河流的纳污能力（水环境容量）是制定该方案的基础。

沙颍河安徽段的主要污染物来自城镇生活废水排放和工业点源污染。根据2012年安徽省环境统计数据，该段共有排污口约166个，其空間分布及排污负荷见图2。

为计算水环境容量，采用重心概化法将干流沿岸的排污口概化为6个排污口。

2 数值模拟

2.1 水流模拟

河流水流过程是水质模拟和水环境容量计算的基础，采用数值方法模拟水流过程。研究仅考虑污染物沿河流流向的一维迁移过程[9]，因此选用一维水动力模型MIKE11的HD模块模拟河流径流量。MIKE11水动力计算模型是基于一维非恒定流Saint -Venant方程组来模拟河流或河口的水流状态.Saint - Venant方程组为

对式（1）采用Abbott -Ionescu六点隐式有限差分格式求解。剖分网格尺寸最大值为5 000 m，并在局部加密，共生成179个计算节点。时间步长为5 min，总计算时段为2 a（2011-01-01-2012-12-31）。以界首闸和沈丘闸实测日流量为上游流量边界，以颍上闸实测日河水位为下游水位边界，初始河水位通过上下游观测水位线性插值获得。采用阜阳闸和颍上闸的实测日流量与水位进行模型率定验证，率定期为2011年，验证期为2012年。根据MIKE11模型按过水断面设置糙率的方法，将断面分为上、中、下三部分，率定参数为断面上、中、下三部分的曼宁糙率n。研究区河道断面变化较大，为有效校正模型[10].断面三部分的初始n值均为0.02[11]。基于观测流量和水位，通过调整参数，获得最佳拟合参数。

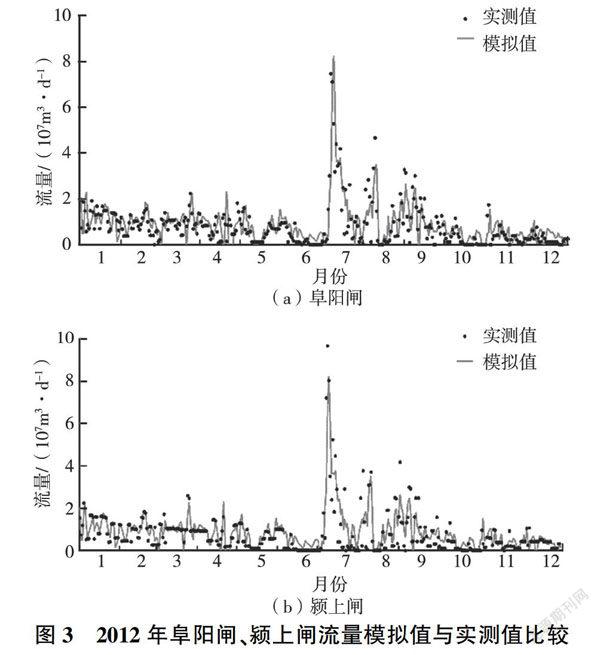
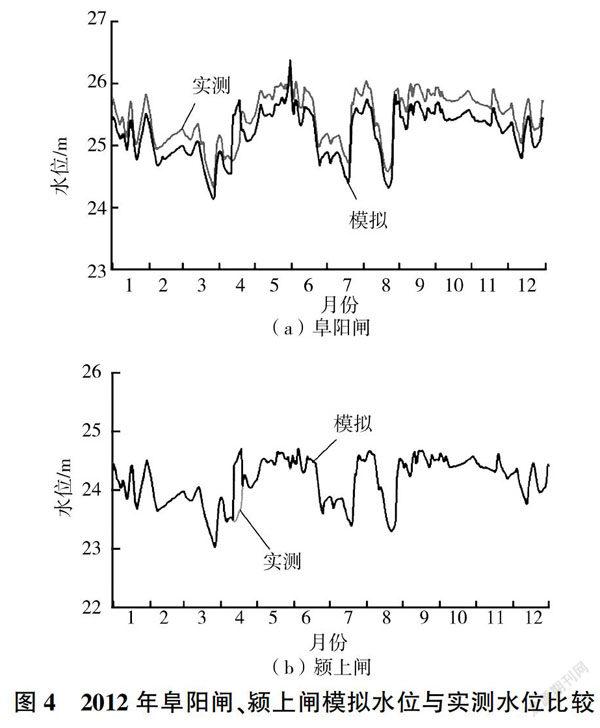
2012年阜阳闸和颍上闸流量与水位的模拟值与观测值见图3、图4.其中：2012年阜阳闸流量的相对误差为11.4%（Nash系数为0.83），水位的相对误差为5.3%（Nash系数为0.93）;颍上闸流量的相对误差为12.3%（Nash系数为0.75），水位的相对误差为0.3%（Nash系数为0.97）。模拟结果基本符合实际水文情况。通过验证，获得断面上、中、下三部分的n值分别为0.020，0.022和0.025。验证的水流模型可用于河流COD和氨氮运移模拟以及水环境容量计算。

2.2 水质模拟

污染物在河流中迁移的控制方程为一维对流弥散方程，考虑一级降解，其方程为

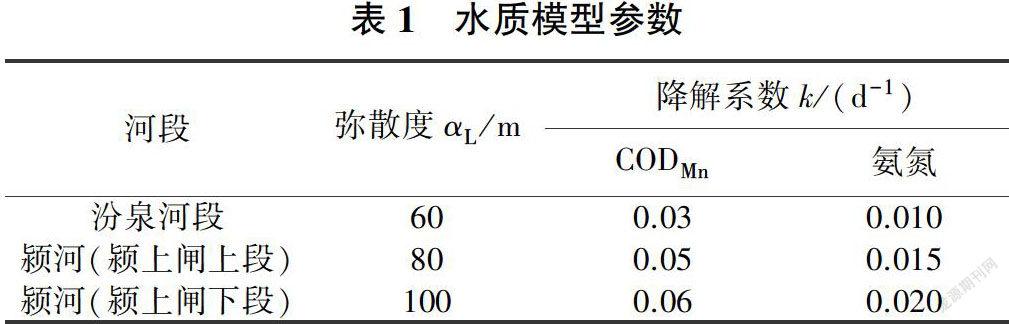
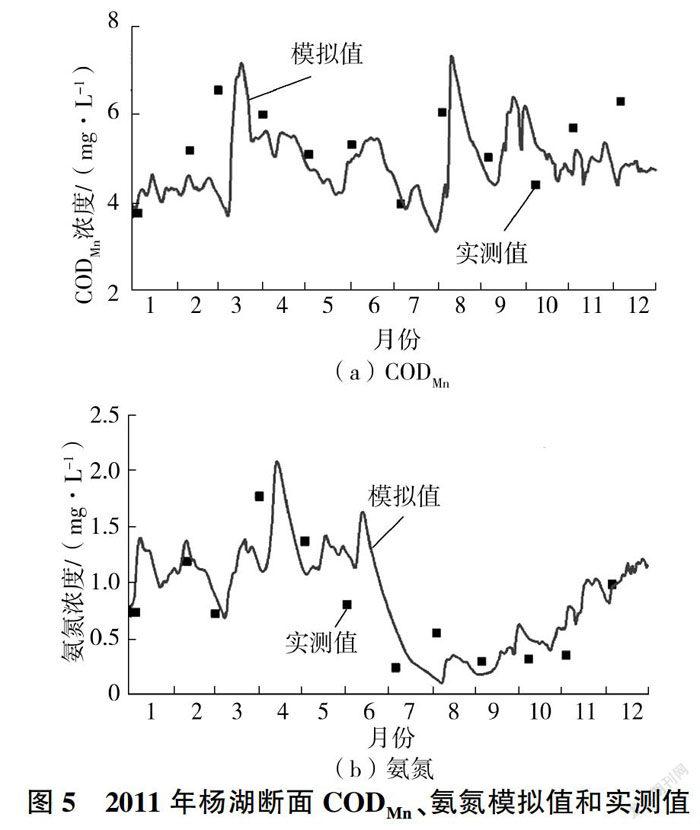
式（3）主要参数是弥敢度a和降解系数k，笔者参考沙颍河流域已有研究成果[12]，选取合适的弥散度a，见表1。姚瑞珍[13]通过室内试验方法确定了CODM。和氨氮在河流中的初始降解系数k分别为0.053 6和0.034 9，并基于实测杨湖断面水质，通过敏感度分析及手动调整参数，获得了最佳拟合参数，见表1。2011年杨湖断面水质模拟值和实测值见图5，其中COD模拟的相对误差为28%，氨氮模拟的相对误差为10%.水质模型基本符合实际情况，可用于沙颍河安徽段的水环境容量计算。

数值模型网格剖分方式及尺寸与水流模型相同，计算节点位置与水流交叉分布。模拟时间步长与计算时段亦与水流模型设置相同。以往水环境容量计算以水质目标值代替上游来水水质的真实值，忽略了上游输入的污染负荷对计算河段环境容量的影响。研究区上游为豫皖省界断面，该断面水质的变化对安徽段水环境容量有不可忽略的影响，因此以上游豫皖省界断面每周观测的水质为模型上游边界的浓度进行计算。

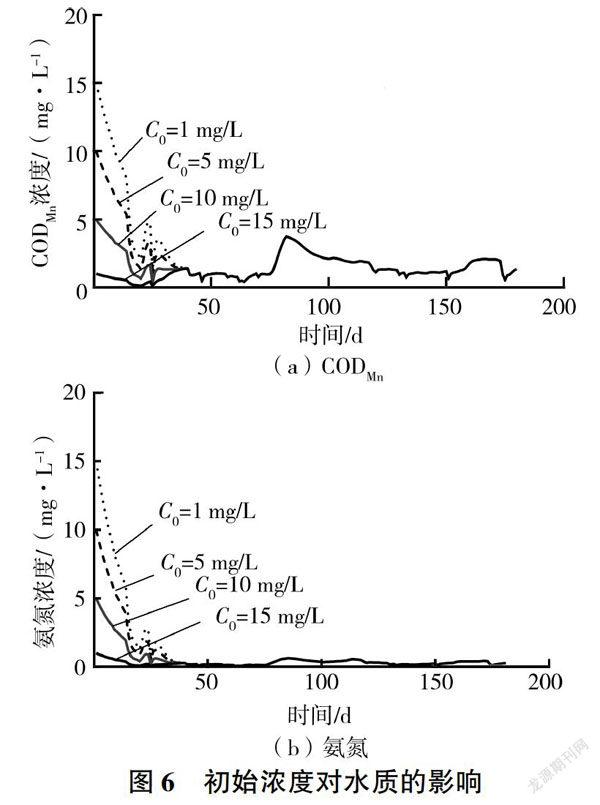
为获取研究区河流的背景值（考虑上游污染负荷输入）.以上游豫皖省界断面实测水质为模型上游边界，假设区内排污量为0，计算2011-2012年河流污染物浓度。由于研究区实测水质资料缺乏，无法给定符合实际的初始浓度，因此采用数值模拟方法估算初始条件影响范围，以此消除初始条件对水质模拟的影响。具体方法为，假设4组COD和氨氮的初始浓度值（C0）分别为1、5、10、15 mg/L。采用上述边界条件及参数，计算人淮口浓度时间序列（见图6）。从图6可以看出，当COD和氨氮模拟时间为50 d时，初始条件的影响可忽略（浓度差别小于0.03 mg/L）。因此选取第51 d的模拟浓度值为初始条件，作为河流背景浓度值的估算值，用于河流氨氮和COD的迁移转化过程模拟。

3 水环境容量计算

针对水功能区划及水质目标[8]，划定3个水环境容量计算单元及相应的控制断面（见图2），控制断面的水质目标均为Ⅲ类。以往的水环境容量研究大都采用单一的水文设计条件，而根据不同的水文条件计算出的结果差别较大，利用最枯流量计算的结果往往严重低于实际环境容量值[14]。为了解实际动态水环境容量动态特征，从2010-2014年日观测数据中选取2012年作为水文设计条件，通过线性规划模型及水质模拟，计算出各排污口允许最大日排污量及河流日环境容量，累加可得排污口允许最大年排污量和河流月环境容量。

由于对流弥散方程是线性的，具有可叠加性，因此可以把多个排污口对控制断面水质的综合影响划分为单个排污口对其影响的线性叠加[15]。基于叠加原理，李适宇等[16]提出贡献度的概念，结合线性规划法求解环境容量。该方法的思路：设某个排污口（i）单位时间排放单位负荷，而其他排污口无负荷量排放，背景浓度值为0，采用一维水质模型计算各水质控制断面（j）的浓度值，该浓度值即为i排污口对各断面的污染贡献度（a）;改变排污口，重复以上步骤，即可求出每个排污口的污染贡献度：基于排污口的污染贡献度，考虑河流背景浓度值，以控制断面水质目标为约束，建立线性规划模型的约束条件，确定目标函数，即总排污负荷最大（环境容量）。具体目标函数为

4 结果与讨论

4.1 排污口环境容量

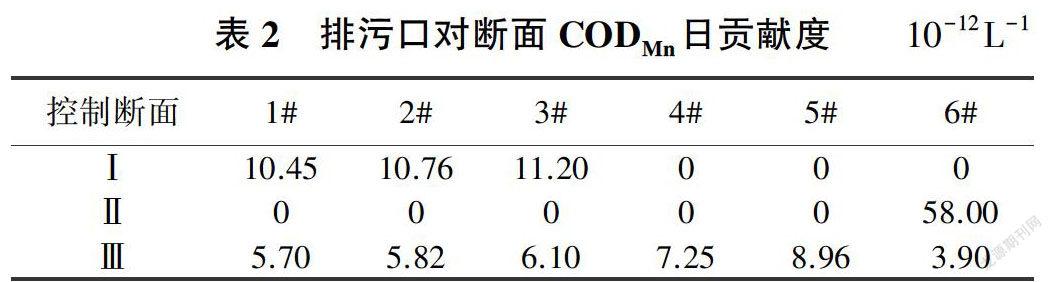
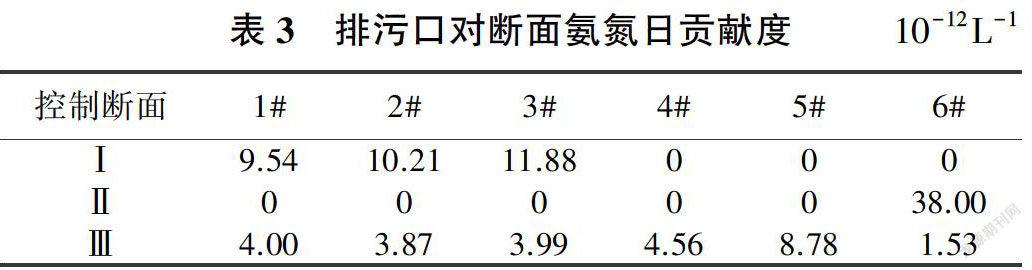
采用MIKE11模型计算出各排污口对各控制断面COD和氨氮的贡献度，年均日贡献度见表2、表3（其中0表示排污口不在此断面控制范围内）。可以看出，排污口1#、2#、3#对控制断面I的贡献度基本相等;仅排污口6#对控制断面Ⅱ有贡献;所有排污口对控制断面Ⅲ均有贡献，其中排污口5#贡献度最大，排污口6#贡献度最小。排污口离控制断面越近，贡献度越大，即排污口对控制断面的影响随距离的减小而增大。

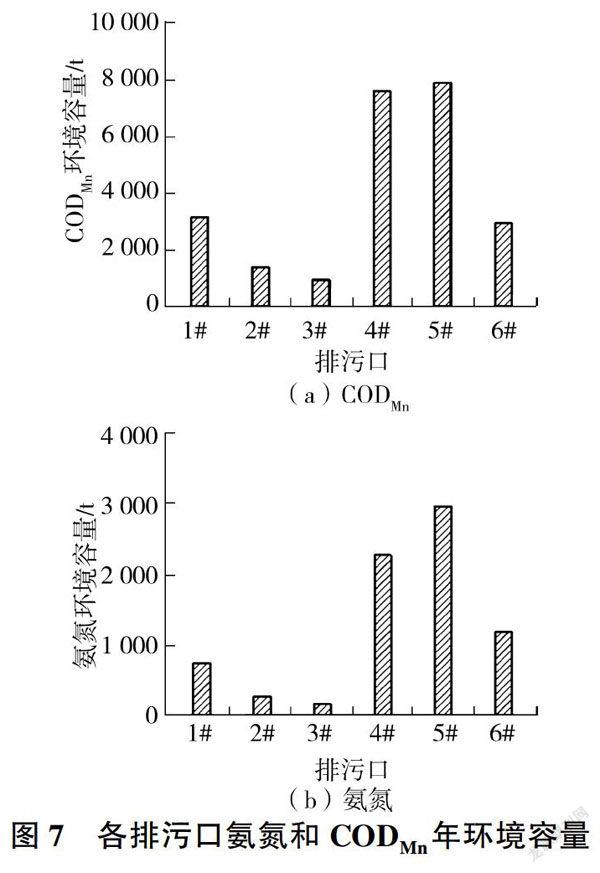
基于排污口对各断面的贡献度，利用线性规划模型计算出2012年各排污口的环境容量，結果见图7。沙颍河安徽段COD环境容量约2.39万t/a，氨氮环境容量约0.76万t/a。其中：排污口5#的COD和氨氮容量最大，分别为7 892、2 970 t/a，占总水环境容量的38.90/0和32.9%;排污口3#的COD和氨氮环境容量最小，分别为948、165 t/a，仅占总水环境容量的3.9%和2.2%。原因是：排污口5#主要受断面Ⅲ控制，对断面I和断面Ⅱ的贡献度为0，受到的限制较小;而排污口3#对断面I和断面Ⅲ的贡献度较大，受到的限制较大。排污口4#、5#、6#的环境容量较大，而排污口1#、2#、3#的环境容量较小，原因是上游来水（省界断面）COD和氨氮浓度较大，大部分时期超过Ⅲ类水质标准，余留的环境容量小，而随水流过程中污染物的降解和稀释，下游的环境容量逐渐增大。

4.2 月环境容量变化分析

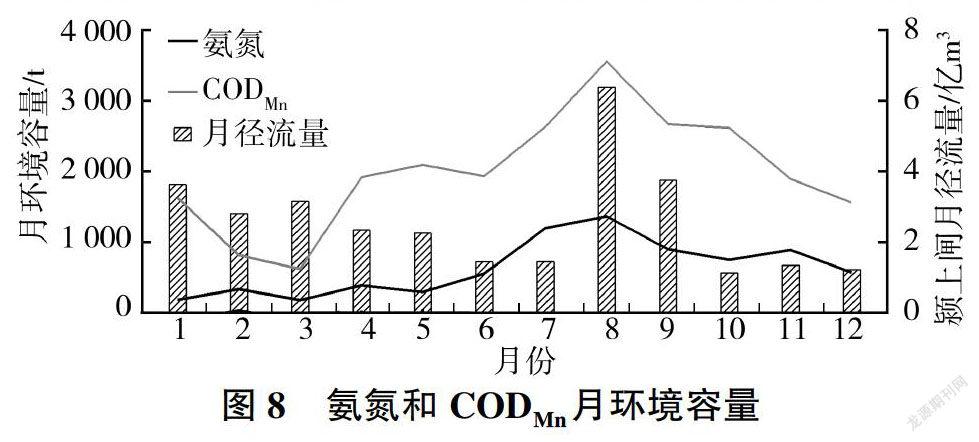
2012年沙颍河安徽段月水环境容量及河流月径流量见图8。从图8可知，COD和氨氮水环境容量年内变幅较大，丰水期（7-10月）环境容量较大，枯水期（11月至翌年5月）环境容量较小。COD和氨氮环境容量均在8月最大，分别为3 557、1363 t;COD和氨氮环境容量在3月最小，分别为621、181 t;氨氮和COD环境容量的变化趋势与径流量不完全一致，1-7月径流量逐渐减少，而COD和氨氮环境容量逐渐增大，直到8月随径流量增大而达到顶峰，说明水环境容量受径流量、上游来水水质等因素的综合影响。

4.3 省界水质对环境容量的影响

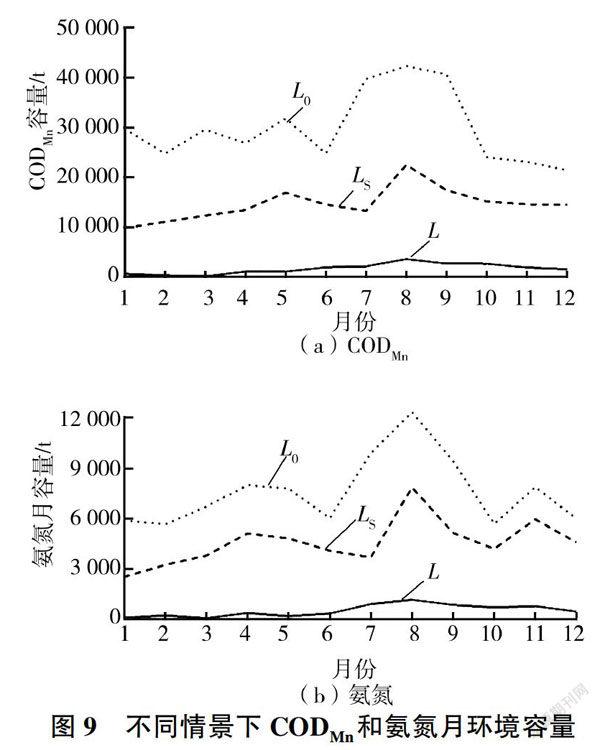
为分析省界断面水质对沙颍河安徽段环境容量的影响，设定3种情景讨论环境容量的变化。情景1为省界断面COD和氨氮浓度为0（即无负荷补给）、背景CODM。和氨氮浓度为0，计算水环境容量（L0）;情景2为省界断面水质为Ⅲ类水（水质目标），计算水环境容量（L）;情景3为省界断面COD氨氮浓度为实测值（实际情况），计算COD、氨氮环境容量（L）。

3种情景月水环境容量见图9。在无上游污染负荷输入的情景1下，环境容量最大，COD、氨氮年容量分别为36.0万、9.1万t：上游污染负荷达标排放情景下，环境容量较小，河段的环境容量主要来自CODM。和氨氮在河流中天然降解量.COD、氨氮年容量分别为17.5万、5.5万t;情景3，环境容量最小，COD、氨氮年容量分别为1.96万、0.62万t.水环境容量仅约为情景2的9%。COD和氨氮的环境容量均为L0>L>L，说明上游水质越差，水环境容量越小。

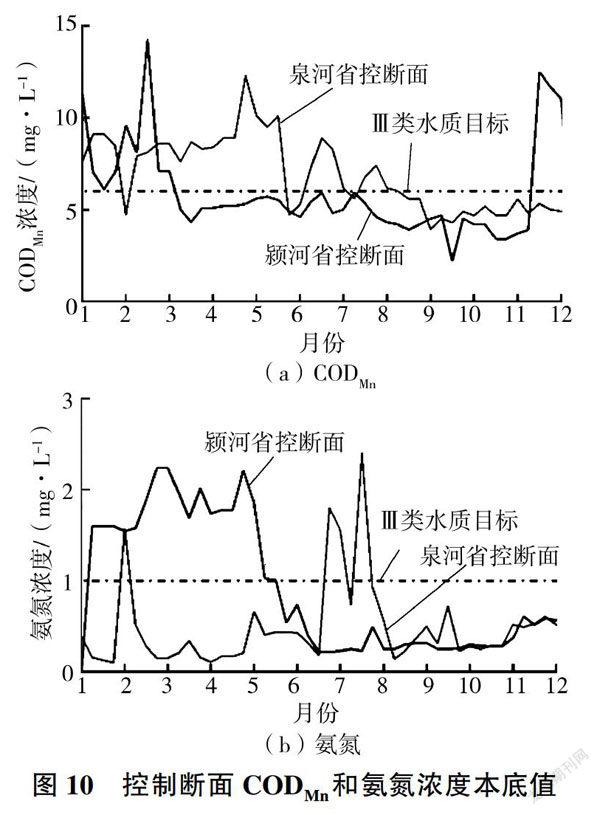
2012年豫皖省界断面水质情况见图10.由图10可知，COD的超标率在泉河省控断面达到55%，在颍河省控断面达到29%：氨氮的超标率在泉河省控断面达到18%.在颍河省控断面达到46%，水质达标率较低。其中，COD超标时间主要为1-6月，氨氮超标时间主要为1-6月（颍河省控断面）和6-9月（泉河省控断面）。由此可见，水环境容量除受河流流量控制外，还受上游水质的影响。

5 结论

基于河流流量及水质观测数据，利用MIKE11水流及水质模型，结合线性规划法，计算沙颍河流域安徽段水环境容量，并分析水环境容量影响因素，结果表明：MIKE11模型对水文和水质的模拟基本符合实际水文情况，模拟结果与实测数据基本一致;沙颍河安徽段COD№、氨氮年环境容量总和约为2.39万、0.76万t/a，COD和氨氮水环境容量年内变幅较大，8月容量最大，分别为3 557、1 363 t，3月容量最小，分别为621、181 t：上游水质对沙颍河安徽段水环境容量影响较大，实际水环境容量仅为上游水质达标（Ⅲ类水）前提下理论水环境容量的9%。

参考文献：

[1] 张玉清，张蕴华，张景霞，河流功能区水污染物容量总量控制的原理和方法[J].环境科学，1998，19（增刊1）：23-33.

[2] 张永良，水环境容量基本概念的发展[J].环境科学研究，1992，5（3）：59-61.

[3]孟偉，张楠，张远，等，流域水质目标管理技术研究（I）：控制单元的总量控制技术[J].环境科学研究，2007，20 （4）：1—8.

[4]姜欣，许士国，练建军，等，北方河流动态水环境容量分析与计算[J].生态与农村环境学报，2013，29（4）：409-414.

[5]郑孝宇，褚君达，朱维斌，河网非稳态水环境容量研究[J].水科学进展，1997，8（1）：25-31.

[6]周孝德，郭瑾珑，程文，等，水环境容量计算方法研究[J].西安理工大学学报，1999，15（3）：1-6.

[7] 董飞，刘晓波，彭文启，等，地表水水环境容量计算方法回顾与展望[J].水科学进展，2014，25（3）：451-463.

[8]郝守宁，颍河流域水功能区面源污染控制研究[D].郑州：华北水利水电大学，2014：1-2.

[9]逄勇，陆桂华，水环境容量计算理论及应用[M].北京：科学出版社，2010：4.

[10] 中国环境规划院，全国水环境容量核定技术指南[R].北京：中国环境规划院，2003：46-76.

[11] 陈炼钢，施勇，钱新，等，闸控河网水文一水动力一水质耦合数学模型：Ⅱ应用[J].水科学进展，2014，25（6）：856-863.

[12] 刘玉年，施勇，程绪水，等，准河中游水量水质联合调度模型研究[J].水科学进展，2009，20（2）：177-183.

[13] 姚瑞珍，人工控制的半封闭河流水环境容量测算研究：以老府河为实例[D].武汉：华中科技大学，2006：34-43.

[14] 李红亮，王树峰，不同设计水文条件下河北省水功能区纳污能力研究[J].南水北调与水利科技，2010，8（3）：68-70.

[15] LIS Y， TOHRU M. Optimal Allocation of Waste Loadsin aRiver with Probabilistic Tributary Flow Under TransverseMixing[ J]. Water Environment Research， 1999， 71（2）： 156-162.

[16] 李适宇，李耀初，陈炳禄，等，分区达标控制法求解海域环境容量[J].环境科学，1999，20（4）：97-100.