低速无人驾驶车辆双向行驶控制方法
柴梦娜 刘元盛 任丽军

[摘要]针对无人驾驶车辆在复杂景区场景低速双向行驶的问题,概述了正向行驶的运动学模型及其跟踪结果,并且在分析车辆倒车运动学模型的基础上,提出一种基于模型预测控制理论的无人驾驶车辆双向轨迹跟踪控制方法。对该双向轨迹跟踪控制方法使用MATLAB工具进行仿真,并在实车上进行验证。结果表明,该方法可以保证无人驾驶车辆稳定地进行双向跟踪参考轨迹行驶。
[关键词]无人驾驶;运动学模型;模型预测控制;倒车轨迹跟踪
[中图分类号]U 469[文献标志码]A[文章编号]10050310(2019)01004908
Twoway Driving Control Method for Lowspeed Autonomous Vehicles
Chai Mengna1,Liu Yuansheng2,Ren Lijun3
(1. Smart City College, Beijing Union University,Beijing 100101,China; 2. College of Robotics, Beijing Union University,
Beijing 100101,China; 3. Beijing Key Laboratory of Information Service Engineering, Beijing
Union University,Beijing 100101,China)
Abstract: To solve the problem of lowspeed twoway driving for autonomous vehicles in complex scenic scenes, a new twoway trajectory tracking control method is proposed. Firstly, the kinematics model of forward driving and its tracking results are briefly summarized. Then based on the analysis of vehicle reversing kinematics model,we propose a twoway trajectory tracking predictive control method for autonomous vehicles. Finally, the simulation is carried out by using MATLAB and the real autonomousdriving verification is also carried out. The results show that the proposed method ensures the autonomous vehicle can track the reference trajectories in two directions stably.
Keywords: Autonomous driving; Kinematic model; Model predictive control; Reversing trajectory tracking
0引言
無人驾驶车辆是未来智能交通系统的有机组成部分,应用在园区或景区有其重要意义。然而,园区或景区道路狭窄,通常不具备车辆掉头的可能性,若要使无人驾驶真正应用到园区或景区等狭窄道路,则要求无人驾驶车辆拥有良好的双向轨迹跟踪能力。轨迹跟踪控制要求无人驾驶车辆能够稳定且无偏差地沿着参考路径行驶[1]。然而,现有的控制方法大多研究车辆向前行驶轨迹跟踪,鲜有对于车辆倒车行驶的研究。目前常用的控制方法分为两类:基于几何追踪的方法和基于模型预测的方法。
纯追踪模型是一种基于几何的控制方法,它可以用来计算车辆在运动中从当前位置到目标点走过的弧形轨迹。段建民等[2]采用纯追踪方法计算前轮偏角控制量,并在实车上进行测试,结果表明该算法跟踪偏差较小且前轮摆动幅度适中。纯追踪算法没有明确的前视距离,当速度发生变化时,该方法不能进行很好的轨迹跟踪。PID控制器是一个在工业控制应用中常见的反馈回路部件[3]。一些研究者采用改进的PID控制方法进行智能车辆路径跟踪[48]。PID控制器算法的控制参数对车辆参数变化非常敏感,无法同时满足对设定值跟踪和抑制外扰的不同性能要求。除此之外,前馈–反馈跟踪控制器也是近年来采用较多的一类跟踪控制方法,前馈控制器主要进行参考路径曲率变化的干扰量补偿,反馈控制主要根据车辆状态反馈调整控制输入,使得扰动和模型误差对跟踪的影响最小化,使车辆更接近期望路径并保持稳定[9]。
基于模型预测的控制方法包括线性二次型调节器 (Linear Quadratic Regulator,LQR)和模型预测控制(Model Predictive Control, MPC)。徐强等[10]指出LQR控制算法的一个重要问题是减小结构的自由度,并提出一种基于合成模型的LQR控制算法,使得在拥有良好准确性的基础上,比传统的LQR控制算法具有更高的计算效率。在一些研究中采用模型预测控制方法进行轨迹跟踪,将车辆简化为二自由度自行车模型,在对车辆模型进行运动学分析的基础上,加入了动力学约束[1115]。与其他控制算法相比,预测控制最大的优点在于它具有显式处理约束的能力,通过把约束加到未来的输入、输出或状态变量上, 可以把约束显式表示在一个在线求解的二次规划或非线性规划问题中,适用于不易建立精确数学模型且存在约束条件的控制系统。
上述方法都未提及倒车行驶的跟踪控制,本文针对车辆在受限于园区环境条件下需进行双向行驶的问题,在分析车辆运动学模型预测基础上,提出了基于模型预测控制的车辆双向行驶方法。在MATLAB平台上进行了仿真,且进行了实车验证。
1控制系统结构
11模型预测控制简述
模型预测控制(MPC)通常在更短的时间跨度内解决优化问题,因此可能会得到次优解。然而,由于MPC对线性没有任何假设,它可以处理硬约束以及非线性系统从其线性化操作点的偏移。模型预测控制由如下3個要素组成:
1) 预测模型:预测控制应具有预测功能,即能够根据系统现在时刻的控制输入以及过程的历史信息,预测过程输出的未来值。
2) 在线滚动优化:预测控制是一种优化控制算法,需要通过某一性能指标的最优化来确定未来的控制作用,使得在这种控制输入下,预测模型的输出与参考值的差距最小。
北京联合大学学报2019年1月
第33卷第1期柴梦娜等:低速无人驾驶车辆双向行驶控制方法
3) 反馈校正:在预测控制中,采用预测模型进行过程输出值的预估只是一种理想的方式,在实际过程中,由于存在非线性、模型失配和干扰等不确定因素,基于模型的预测不可能准确地与实际相符。因此,在预测控制中,通过输出的测量值与模型的预估值进行比较,得出模型的预测误差,再利用模型预测误差来对模型的预测值进行修正。到下一个时间点,再根据新的状态重新进行预测和优化。
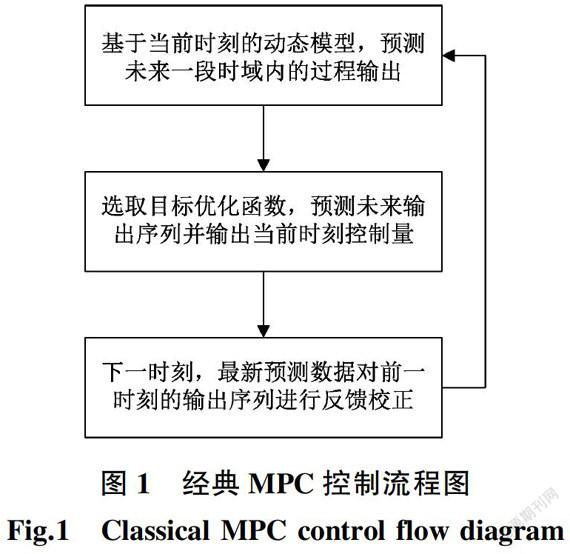
经典MPC控制流程图如图1所示。
图1经典MPC控制流程图
Fig.1Classical MPC control flow diagram
12车辆双向运动学模型
车辆向前行驶时,为后轮驱动、前轮转向;在进行倒车行驶时,为前轮驱动、前轮转向,两者在运动学的建模上存在较大区别。由于对车辆前向行驶运动学分析的文献较多,因此本文不再进行具体分析。
本文采用四轮车辆模型来分析车辆的运动情况。在对车辆运动学建模时进行如下假设:车辆只作平行于地面的平面运动,俯仰角和侧倾角均为零;忽略空气阻力和车辆悬架特性;车辆前轮的转向角度始终保持一致。车辆运动学模型如图2所示,其中XOY为大地坐标系。
图2车辆运动学模型
Fig.2Vehicle kinematics model
图中Xf,Yf) 为车辆前轴轴心,Xr,Yr) 为车辆后轴轴心,φ为车体横摆角,δf 为前轮偏角,vf 为车辆前轴中心速度,vr 为车辆后轴中心速度,l为车辆轴距。速度向前为正,向后为负。
图3车辆倒车模型预测控制结构图
Fig.3Vehicle reversing MPC structure diagram
1) 车辆前向运动学模型为
X
·rY·r
φ·=
cos φ
sin φ
tan δf/lvr。
(1)
2) 车辆倒车运动学模型分析
在后轴行驶轴心Xr,Yr)处,速度为
vr=X·r
cos φ+Y·r
sin φ。
(2)
根据车辆前后轴运动学约束有:
X·fsin φ+δf-Y
·fcos φ+δf=0X·rsin φ-Y
·rcos φ=0。(3)
根据车辆前后轮间的几何关系得:
Xr=Xf-lcos φYr=Yf-l
sin φ
。(4)
将式(4)求导后得:
Xr
·=Xf·+φ·lsin φYr·=Yf·-φ·lcos φ。(5)
根据式(3)和式(5)可得:
φ·=-
sin δfl×vf。
(6)
至此,得到车辆倒车运动学模型为
X
·fY
·f
φ·=cos (φ-δf)sin (φ-δf)-sin δf/lvf。
(7)
将车辆输入变量定义为u=(v
δ)T,车辆当前坐标定义为=[X Y φ]T,式(7) 也可写成
ξ·=f(ξ,u)。(8)
2无人车双向轨迹跟踪控制方法
本文提出基于误差模型的双向轨迹跟踪控制方法。在分析车辆倒车运动学模型的基础上,更新了其在模型预测控制中所采用的预测模型。在进行倒车轨迹跟踪时,预测模型的输入为参考路径和车辆当前控制量,包括:参考路径在笛卡尔坐标系下坐标、车辆与X轴夹角、当前车速、前轮偏移角。接下来,通过对带约束目标函数的优化求解,得到与预测时域的控制增量。再将控制增量序列的第一个元素作为实际控制输入量作用于系统,进行反馈控制。至此,完成了对车辆当前时刻的控制。在下一时刻,系统根据状态信息重新预测下一段时域的输出,实现在线滚动优化。车辆倒车模型预测控制结构如图3所示。
21预测模型
车辆倒车运动学模型式(8)为非线性模型,由于非线性模型求解的复杂性,首先将非线性模型通过在采样时刻较小时差分代替微分的方法,将非线性模型转化为线性模型再进行求解。
参考系统的任意时刻的状态和控制量满足如下关系:
ξr·=f(ξr,ur)。(9)
在任一点(ξr,ur)处进行泰勒展开,只保留一阶项,忽略高阶项,得到:
ξ·=fξr,ur+f
ξξ=ξr
u=ur
(ξ-ξr)+
fu
ξ=ξr
u=ur(u-ur)。(10)
将式(10)减去式(9)可得:
ξ·=A(t)ξ+B(t)u。(11)
式中:ξ=ξ-ξr, u=u-
ur,
A(t)=
Jf(ξ),
B(t)=
Jf(u)。
其中:Jfξ为
f对ξ的雅可比矩阵,Jfu为f对u的雅可比矩阵,进行近似的离散化处理,得:
Ak,t=I+TA(t),(12)
Bk,t=TB(t)。(13)
结合式(11)、(12)和(13)得:
ξ(k+1)=Ak,tξ(k)+Bk,t
u(k)。(14)
求解得:
1) 正向行驶
A(k)=10-vr(k)sin φkT01vr(k)cos φkT001,(15)
B(k)
=cos φkT0sin φkT0tan δrkTlvrkTlcos2δr(k)。(16)
2) 倒车行驶
A(k)=10-vf(k)sin(φ-δ)kT01vf(k)cos(φ-δ)kT001,
(17)
B(k)
=cos(φ-δ)kTvf(k)sin(φ-δ)kTsin(φ-δ)kT-vf(k)cos(φ-δ)kT-sin δfkTl-vfkcos δfkTl。
(18)
其中:k表示采样时间, T表示采样周期。
22优化求解
在车辆轨迹跟踪控制中,将k时刻的优化目标函数定义为
Jk=Nj=1[ξTk+j|kQξk+j|k+
uTk+j|k+j-1Ruk+j|k+j-1]。(19)
通过对以上优化目标进行适当处理,可将其转化为二次规划问题。通过将控制增量作为优化解,可将优化目标设为:
J(ξt,ut-1,ΔUt)=
Npi=1
ξt+i|t-ξr(t+i|t)2Q+
Nc-1i=1
Δut+i|t2R。
(20)
其中,第一项反映了系统对参考轨迹的跟踪能力,第二项反映了对控制量平稳变化的要求。Q和R为权重矩阵。
对目标函数添加控制增量约束:
Δumint+k≤Δut+k≤Δumaxt+k,
k=0,1,…,Nc-1。
(21)
參考轨迹与测试时域内输出量的偏差表示为
Et=Ψt
ξt|t-Yreft,
(22)
Yref=[ξreft+1|t,…,ξreft+Np|t]T。(23)
将目标函数转化为矩阵形式,可等价于求解以下二次规划问题:
minΔUt
(ΔUtHtΔUtT+GtΔUtT),
(24)
ΔUmin≤ΔU(k)≤ΔUmax,k=t,…,t+Hc-1。
(25)
其中:Ht=ΘtTQeΘt+Re,Gt=2EtQeΘt。
Θt=Bt0
00
AtBtBt00
………
AtNc-1Bt
AtNc-2
Bt…
Bt
AtNc
Bt
AtNc-1Bt…
AtBt
AtNP-1Bt
AtNP-2Bt…
AtNP-Nc-1Bt
,(26)
Qe=Q00Q…0…000…Q,(27)
Re=R00R…0…000…R。
(28)
Qe为误差权矩阵,Re为控制权矩阵。
23反馈控制
在每个控制周期内完成对上述二次规划问题求解后,得到控制时域内的一系列控制输入增量:
ΔUt*=[Δut*,Δut+1*,…,Δut+Nc-1*]T。(29)
系统未来时刻的预测输出以矩阵形式表达:
Yt=
Ψtξ
(t|t)+ΘtΔU(t)。
(30)
其中:
Yt=
ξ(t+1|t)
ξ(t+2|t)…
ξ(t+Nc|t)…
ξ(t+Np|t),(31)
Ψt=AtAt2…AtNc…AtNp,(32)
ΔUt=Δut|t
Δut+1|t…
Δu(t+Nc|t)。
(33)
由于非线性模型转化为线性模型存在误差,故根据模型预测控制的基本原理,将该控制序列中的第一个元素作为实际的控制输入增量,作用在非线性运动学模型上求解,得到车辆下一时刻真实状态为
u(t)=
u(t-1)+Δut
*。(34)
系统执行这一控制量直到下一时刻,在新的时刻,系统根据状态信息重新预测下一段时域的输出,通过优化过程得到一个新的控制增量序列。如此循环往复,直到系统完成控制过程。
3结果与分析
31仿真实验
为验证提出模型控制方法的跟踪性能,利用所提出的模型在两种典型的工况下对双向行驶进行MATLAB仿真。考虑到乘坐舒适性,选择控制增量约束值小,且车辆倒车速度不宜过高,故实验均在低速情况下进行。实验包括直线轨迹跟踪的正向行驶和倒车行驶、圆形轨迹的正向行驶和倒车行驶。
不同仿真工况下,初始车速依次设为3 km/h、5 km/h和10 km/h,在跟踪图中分别以红色、绿色、黑色表示。参考轨迹以蓝色表示。
311直线轨迹跟踪情况下的结果分析
初始车辆偏移角设为0,采样周期设为005 s,预测时域为45。对车辆控制增量约束为-22≤Δv≤22,
-064≤Δw≤064。状态量的权重矩阵为
Q=08000100005,R=010001。
1) 正向行驶
车辆初始位置为ξ0=
[00pi/6],轨迹跟踪情况如图4(a)、4(b)和4(c)所示。
图4直线轨迹跟踪情况下正向行驶结果
Fig.4Forward driving result with linear
trajectory tracking
2) 倒车行驶
车辆初始位置为ξ0=
[255pi/6],轨迹跟踪情况如图5(a)、5(b)和5(c)所示。
图5直线轨迹跟踪情况下倒车行驶结果
Fig.5Reverse driving result with linear
trajectory tracking
从图4(a)和图5(a)中可看出,车辆初始位置处纵向位置相对于第一个参考点,均偏移5 m。由于初始位置相对于参考轨迹的位姿存在差异,所以完全跟踪上参考轨迹的时间存在差异。但是在正向行驶和逆向行驶中均可看出,当车速设置较高时,会更快地跟踪上参考轨迹。在其他控制参数相同情况下,不同的车速都可使车辆快速跟踪上轨迹,体现了模型对速度的鲁棒性。图4(b)和图5(b)展示了不同车速下车辆纵向速度随时间变化的曲线,可以看出纵向速度最终趋于一个固定值,其为参考轨迹车速,且车速变化在给定约束范围内。图4(c)和图5(c)展示了不同车速下车辆前轮偏角随时间变化的曲线,由于为直线轨迹,故在稳定时最终角度趋于0,且偏移角的变化在给定约束范围内。
312圆形轨迹跟踪情况下的结果分析
轨迹半径为10 m,初始车辆偏移角设为0,采样周期设为005 s,预测时域为60。对车辆控制增量约束为-22≤Δv
≤22,-22≤Δw≤22。状态量的权重矩阵为
Q=08000100005,R=050005。
1) 正向行驶
车辆初始位置为ξ0= [9990 10628 2pi/2],轨迹跟踪情況如图6(a)、6(b)和6(c)所示。
图6圆形轨迹跟踪情况下正向行驶结果
Fig.6Forward driving result with circular
trajectory tracking
2) 倒车行驶
车辆初始位置为 ξ0= [9990 10628 24743 8],轨迹跟踪情况如图7(a)、7(b)和7(c)所示。
从图6(a)和图7(a)中可看出,车辆初始位置位于第一个参考点处。正向行驶的跟踪效果优于逆向行驶,车速越高偏离参考轨迹越多。在其他控制参数相同情况下,不同的车速都可使车辆快速跟踪上轨迹,体现了模型对速度的鲁棒性。图6(b)和图7(b)展示了不同车速下车辆纵向速度随时间变化的曲线,可以看出纵向速度最终趋于一个固定值,其为参考轨迹车速,且变化在给定范围约束内。图6(c)和图7(c)展示了不同车速下车辆前轮偏角随时间变化的曲线,由于为圆形轨迹,故在稳定时最终角度趋于一个固定值,为参考轨迹偏角,且变化在给定约束范围内。
32实车试验
为验证控制算法的有效性,在小旋风第四代无人驾驶车上做了实车试验,如图8所示。参考轨迹车速为3 km/h,初始车速为3 km/h,车辆轴距为34 m,速度和转角增量范围分别为2 km/h和60°。
采集的数据为经纬度信息,将其数据进行处理。
用蓝线表示参考轨迹,红线表示实际轨迹。
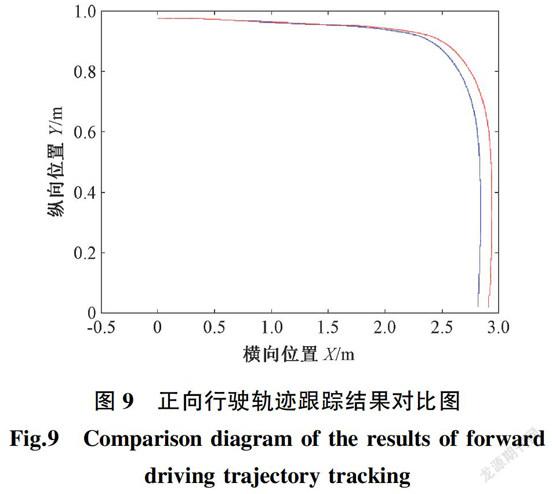
正向轨迹跟踪结果如图9所示,图中的起点坐标为(290,002),车辆起始前轮偏角为0°。
倒车轨迹跟踪结果如图10所示,图中的起点坐标为 (1,092),车辆起始前轮偏角为180°。
图7圆形轨迹跟踪情况下倒车行驶结果
Fig.7Reverse driving result with circular
trajectory tracking
图8小旋风无人驾驶车辆
Fig.8“Cyclone” autonomous vehicles
从图中可看出,试验车最终均可稳定地跟踪上参考轨迹,证明本文提出的双向轨迹跟踪控制算法是可行的。
图9正向行驶轨迹跟踪结果对比图
Fig.9Comparison diagram of the results of forward
driving trajectory tracking
图10倒车行驶轨迹跟踪结果对比图
Fig.10Comparison diagram of the results of reverse
driving trajectory tracking
4总结与展望
在一些园区或景区情况下,车辆倒车难度极
大,甚至无法倒车,故本文提出了基于模型预测控制的低速车辆双向控制方法,在MATLAB上针对不同工况进行了仿真验证,并进行了实车验证,结果表明提出的方法可以较好地进行倒车轨迹跟踪。文中所提方法只涉及运动学约束,没有深入考虑车辆在轨迹跟踪过程中的各种动力学约束。后续的研究应该将车辆的动力学约束考虑在内,使车辆可以在不同道路环境下跟踪性能更优。车辆倒车轨迹跟踪与车辆向前行驶的轨迹跟踪方法相似。目前基于模型预测控制的车辆轨迹跟踪方法在动力学与运动学约束上依然作了很多假设,这些假设简化了模型,极大提高了在线优化的计算速度,但是模型的不精确同样导致车辆实际输出与预测输出的误差,后期的研究方向应在计算量大小不影响车辆实时跟踪情况下,车辆预测模型更加精确。[参考文献]
[1]龚建伟,姜岩,徐威.无人驾驶车辆模型预测控制[M].北京:北京理工大学出版社,2014:33-35.
[2]段建民,杨晨,石慧.基于Pure Pursuit算法的智能车路径跟踪[J].北京工业大学学报,2016,42(9):1301-1306.
[3]柴梦娜,刘元盛,任丽军. 无人驾驶车辆路径跟踪控制方法的研究与发展[J]. 计算机科学,2018,45(10A):200-202.
[4]谭宝成,王宾.无人驾驶车辆路径跟踪的增量式PID控制[J].西安工业大学学报,2016,36(12):996-1001.
[5]Ozana S, Docekal T. PID controller design based on global optimization technique with additional constraints[J]. Journal of Electrical Engineering, 2016, 67(3):160-168.
[6]丁鹏,李林升,钟成.基于改进BP神经网络的智能车PID控制研究[J].机械工程师,2018(3):9-11.
[7]贾志祥,孙兆帅.基于模糊PID和前馈控制的智能车速度控制[J].中国战略新兴产业,2018(4):179.
[8]陈冠希.模糊自适应PID算法在智能车中的应用研究[J].河南科技,2018(3):31-32.
[9]孙银健. 基于模型预测控制的无人驾驶车辆轨迹跟踪控制算法研究[D].北京:北京理工大学,2015.
[10]徐强,陈健云,李静,等.Study on LQR control algorithm using superelement model[J].Journal of Central South University,2016,23(9):2429-2442.
[11]Schildbach G, Borrelli F. Scenario model predictive control for lane change assistance on highways[C]// Intelligent Vehicles Symposium. IEEE, 2015:611-616.
[12]Kühne F, Fetter W, Joo L, et al. Model predictive control of a mobile robot using linearization[J]. Proceedings of Mechatronics & Robotics, 2004:525-530.
[13]Schildbach G, Fagiano L, Frei C, et al. The scenario approach for stochastic model predictive control with bounds on closedloop constraint violations[J]. Automatica, 2014, 50(12):3009-3018.
[14]余如. 無人驾驶车辆的自动转向控制[D].吉林:吉林大学,2016.
[15]李培新,姜小燕,魏燕定,等.基于跟踪误差模型的无人驾驶车辆预测控制方法[J].农业机械学报,2017,48(10):351-357.

