压力对Cr3Si机械稳定性和韧脆性影响的 第一性原理研究

吕仕莲 陈少波 张殿喜 闫万珺 陈英

摘 要：本文采用基于密度泛函理论的第一性原理方法，对不同压力下Cr3Si的机械稳定性和韧脆性进行研究。通过计算Cr3Si在不同压力下的弹性常数、体积模量、剪切模量、泊松比来分析Cr3Si的机械稳定性和韧脆性质。根据波恩准则判断，Cr3Si在研究压力范围内，满足机械稳定性条件。结果表明，当压力为0～4GPa时，Cr3Si化合物表现为脆性，当压力大于4GPa以后，Cr3Si化合物表现为韧性。

关键词：Cr3Si;第一性原理;机械稳定性;韧脆性

中图分类号：TG142.13 文献标识码：A 文章编号：1003-5168（2019）01-0050-05

First-principles Study on the Effect of Pressure on Mechanical

Stability and Ductile-brittle Properties of Cr3Si

LYU Shilian CHEN Shaobo ZHANG Dianxi YAN Wanjun CHEN Ying

（College of Electronic and Information Engineering， Anshun University，Anshun Guizhou 561000）

Abstract： In this paper， the mechanical stability and toughness and brittleness of Cr3Si under different pressures were studied by the first-principles method based on density functional theory. The mechanical stability and ductile-brittle properties of Cr3Si were analyzed by calculating the elastic constants， bulk modulus， shear modulus and Poisson's ratio of Cr3Si under different pressures. According to Bonn criterion， Cr3Si satisfied the condition of mechanical stability in the range of research pressure. The results show that Cr3Si compounds exhibit brittleness when the pressure is between 0 and 4GPa， and toughness when the pressure is greater than 4GPa.

Keywords： Cr3Si;first-principles;mechanical stability;ductile-brittle properties

1 研究背景

近年来，国内外掀起了研究Cr3Si的热潮，对其耐磨性、耐蚀性和抗氧化性等方面进行了大量研究。过渡金属硅化物Cr3Si具有熔点高、蠕变性能好、高温抗氧化性能好、强度和硬度高、抗热腐蚀性能优异、耐磨性能好、密度相对较高等特点，因此被看作是最理想的新一代高温结构候选材料之一，在制作高温材料这一领域具有良好的应用前景，如航空航天、燃气轮机等领域[1-4]。目前，过渡金属硅化物Cr3Si作为一种新型的高温材料已受到科研人员的高度重视和广泛研究。从一系列的研究[5-10]可知，金属硅化物Cr3Si具有良好的抗氧化性及耐磨耐蚀性。但是，Cr3Si存在的共价键使其在室温环境中很脆、易碎，因此，Cr3Si的耐受性较低[10]。从D.L.Anton[11]等人的研究可以发现，Cr3Si与大量金属化合物一样，在使用时都会出现缺乏室温韧性这一问题。为了使这种材料更适合于结构应用，人们尝试提高这种材料的韧性。T.A.Cruse[10]等人通过研究发现，降低硅含量，生产出由Cr3Si相和纯铬组成的复合材料，能显著提高复合材料的韧性。Bei H等人通过研究发现，Cr3Si共晶合金定向凝固也可以实现Cr3Si的韧性相增韧[12-13]。Newkirk J W[14]等人通过实验，得出了加入韧性相是提高Cr3Si韧性的有效方法之一。Jiang Xu等人[15]采用溅射沉积法研究了块状或涂层材料的纳米晶Cr3Si的力学性能，结果表明，纳米晶Cr3Si薄膜具有较高的延展性或韧性。He Wei等人[16]通过密度泛函理论的第一性原理计算，表明在没有加压力的情况下，Cr3Si化合物具有机械稳定性。但目前，有关金属硅化物Cr3Si在不同压力下机械稳定性韧脆性的研究在国内外都没有系统的研究见诸报端。Cr3Si作为一种潜在的超高温化合物，其机械性、韧脆性和弹性性能对新材料的设计和开发具有重要意义。笔者通过对不同压力下Cr3Si的机械性和韧脆性进行研究，预期为开发和设计新型Cr3Si高温材料做一些基础性的研究工作。

2 計算方法

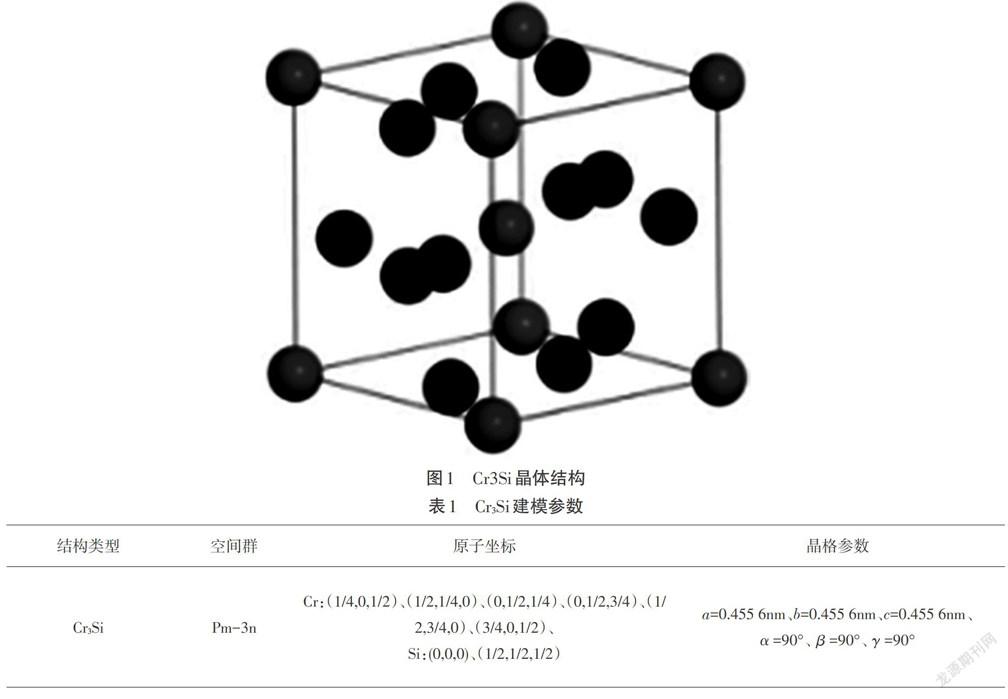
本文的理论计算采用基于密度泛函理论（DFT）[17]的CASTEP软件包。Cr3Si是空间群为PM-3n的立方体结构[18]，晶格常数为a=b=c=4.556Å，Cr3Si的晶体结构如图1所示。用广义梯度近似（GGA）处理电子之间的交换关联能，利用PAW势来描述电子与离子的相互作用，总能量的收敛性判据是10−6eV。经过对截断能和K点的测试，Cr3Si结构平面波的截断能量取450eV，K网点为10×10×10[19]。正确建立Cr3Si化合物的晶体结构模型[18]，如表1所示，利用赝势平面波展开法对模型进行优化，采用基于第一性原理的密度泛函理论来计算不同压力下Cr3Si结构的弹性常数、体模量、剪切模量、泊松比。

3 计算结果与分析

3.1 机械稳定性

弹性常数[Cij]提供了更多关于Cr3Si化合物的机械稳定性、比热、熔点、德拜温度和热膨胀系数的信息。本文采用基于密度泛函理论的第一性原理计算，采用不同的压力计算了Cr3Si的弹性常数。表2列出了Cr3Si压力在0GPa下的弹性常数以及其他理论计算值和实验值。本文的计算结果与其他理论计算结果误差非常小，说明本文的计算具有很高的可靠性。根据计算出的弹性常数，从机械性能方面研究Cr3Si化合物的稳定性，根据波恩准则的晶格动力学理论，结构的力学稳定性的应变能必须在任意均匀弹性变形的条件下为正。众所周知，对于立方晶体，机械稳定性条件是[20]：

[C11>0C11-C12>0C44>0C11+2C12>0]                                        （1）

其中，[C11]表示x方向施加应力在x方向引起的应变，[C12]表示x方向施加应力在y方向引起的应变，[C44]表示在[yz]方向施加应力在[yz]方向引起的应变。

从表2可以看出，压力为0GPa时，计算得到的弹性常数值与上述准则一致，说明Cr3Si化合物具有机械稳定性。在压力为0GPa时，本文计算得到的结果与其他理论计算所得到的结果一致。

在这里，笔者计算了不同压力下的弹性常数，如图2所示。[C44]表示晶体在（100）平面上对剪切应变的阻力，与剪切模量密切相关。同时，[C11]、[C12]均随着压力的升高而快速增加，只有[C44]随着压力的升高基本保持缓慢增加，而在压力增加到2 400GPa时，[C44]开始出现下降趋势。在压力研究范围内，Cr3Si均满足机械稳定性条件。由于GGA方法采用了几何优化的方法，Cr3Si化合物的弹性常数结果可能被高估了。因此，本文利用形成能再次确定Cr3Si化合物的相对稳定性，Cr3Si形成能计算公式为[22]：

[EFE=Etot-NCrECr-NSiESi/NCr+NSi]           （2）

其中，[ECr]和[ESi]分别为一个Cr和Si原子的能量;[NCr]和[NSi]是Cr3Si结构中Cr和Si原子的数量。压力为2 400GPa时，得出的形成能为-1841eV，形成能为负值，且负值越大，说明Cr3Si的机械性越稳定。

3.2 韧脆性

根据计算出的弹性常数，可以计算出体积模量B、剪切模量G、泊松比V。计算体积模量和剪切模量的过程中，有两种不同的理论，分别是Reuss和Voigt理论。通常情况下，用[BV]和[BR]以及[GV]和[GR]分别表示Voigt和Reuss理论下的体积模量和剪切模量。体积模量B、剪切模量G可由Voigt-Reuss-Hill近似得到。Reuss的值和Viogt的值分别表示弹性模量的最大值和最小值，VRH近似是Voigt的下界和Reuss的上界的平均值，其提供了一种利用已知单晶弹性常数估计多晶材料力学性能的方法。对于立方体系，所有的模可通过以下关系得到[16]：

[BV=C11+2C12/3]                               （3）

[BR=C11+2C12/3]                              （4）

[B=Bv+BR/2]                                 （5）

[GV=C11-C12+3C44/5]                            （6）

[CR=5C11-C12C44/4C44+3C11-C12]               （7）

[G=GV+GR/2]                              （8）

[V=3B-2G/23B+G]                           （9）

其中，[BV]、[BR]、B分別为Voigt、Reuss、Voigt-Reuss- hill近似计算的体积模量，[GV]、[CR]、[G]分别为Voigt、Reuss和Voigt-Reuss-Hill近似计算的剪切模量，[V]是泊松比，是由Voigt-Reuss-Hill近似计算得出。Cr3Si化合物各模量的计算结果与其他理论实验值如表3所示。

本文在壓力为0GPa时计算得到的结果与其他理论计算所得到的结果一致，说明对Cr3Si的体积模量B、剪切模量G、泊松比V的计算具有一定的可靠性。众所周知，体积模量反映了固体在静水压力下的压缩性。总的来说，Cr3Si的体积模量比较大，在许多情况下，化合物的体模量越大，硬度越高。在压力为0～6GPa时，Cr3Si化合物的泊松比（V）接近0.3，说明Cr3Si化合物具有较强的金属性质。

根据Pugh方法[23]的准则，用[BG]比值来判断Cr3Si化合物的韧脆性。如果[BG]值低于1.75，则Cr3Si化合物表现为脆性材料，如果[BG]值低于1.75，则Cr3Si化合物表现为韧性材料。此外，还可以通过泊松比（V）的值来判断Cr3Si化合物的韧脆性，当泊松比大于0.25时，Cr3Si化合物表现韧性材料。综合比较计算出来的泊松比与[BG]值可以得出，当压力为0～4GPa时，Cr3Si化合物表现为脆性，当压力大于4GPa以后，Cr3Si化合物表现为韧性。

4 结论

本文利用密度泛函理论的第一性原理计算出Cr3Si化合物的弹性常数、形成能、体积模量、剪切模量、泊松比等，研究和讨论了不同压力下Cr3Si化合物的机械稳定性、韧脆性以及其是否具有金属性质。弹性常数和形成能表明，在压力研究范围内，Cr3Si均满足机械稳定性条件。体积模量、剪切模量和泊松比表明，当压力为0～4GPa时，Cr3Si化合物表现为脆性，当压力大于4GPa以后，Cr3Si化合物表现为韧性。泊松比的计算结果表明，Cr3Si化合物具有较强的金属性质。

参考文献：

[1] Raj S V， Whittenberger J D， Zeumer B， et al. Elevated temperature deformation of Cr3Si alloyed with Mo[J]. Intermetallics， 1999（7）：743-755.

[2] Cruse T A， Newkirk J W. Evaluation of methods to produce tough Cr3Si based composites[J]. Materials Science & Engineering A， 1997（1）：410-418.

[3]Shah D M， Ant on D L. Evaluation of refractory in termetallics with A15 structure for high temperature structural applications[J]. Material Science and Engineering A， 1992（153）： 402-409.

[4]Mattheiss L. Electronic structure of CrSi2 and related refractory disilicides[J]. Physical Review B，1991（15）： 12549-12555.

[5] Raj S V. An evaluation of the properties of Cr3Si alloyed with Mo[J]. Materials Science & Engineering A （Structural Materials：，Properties，Microstructure and Processing），1995（1-2）：229-241.

[6]孙爱民，董显平.不同硅含量Cr3Si基合金的抗氧化性研究[J].实验室研究与探索，2003（3）：38-41.

[7]段刚，赵海云，王华明.激光熔敷Cr3Si/Cr2Ni3Si复合材料涂层组织与耐磨性研究[J].复合材料学报，2002（1）：32-36.

[8]张立强，王华明.Cr3Si/Cr13Ni5Si2金属间化合物合金组织与高温滑动磨损性能的研究[J].稀有金属材料与工程，2004（5）：512-514.

[9] Duan G， Wang H M. High-temperature wear resistance of a laser-clad γ/Cr3Si metal silicide composite coating[J]. Scripta Materialia，2002（1）：107-111.

[10] NewirkJ.W. Abrasive wear properties of Cr-Cr3Si composites[J]. Wear，2001（1）：1361-1371.

[11] Jianhua Ma，Yunle Gu，Liang Shi，et al.Synthesis and oxidation behavior of chromium silicide （Cr3Si） nanorods[J]. Journal of Alloys and Compounds， 2004（375）：249–252.

[12] Bei H， George E P， Pharr G M. Effects of composition on lamellar microstructures of near-eutectic Cr–CrSi alloys[J]. Intermetallics， 2003（4）：283-289.

[13] Bei H， George E P， Pharr G M. Effects of composition on lamellar microstructures of near-eutectic Cr–CrSi alloys[J]. Intermetallics， 2003（4）：283-289.

[14] Wang H M ， Duan G . Microstructure and wear resistance of a laser clad reinforced Cr3Si metal silicide composite coating[J]. Materials Science & Engineering A （Structural Materials： Properties， Microstructure and Processing）， 2002（1-2）：117-123.

[15] Jiang X， Jian S， Jiang S. Mechanical properties of sputter-deposited nanocrystalline Cr3Si film[J]. Materials Letters， 2009（12）：1082-1084.

[16] Wei H， Chen Y L， Su L. Stability， Mechanical Properties and Electronic Properties of X3Si （X=V， Nb， Cr， Mo and W） from First Principles Calculations[J]. Materials Science Forum， 2018（913）：596-606.

[17] Segall M D， Lindan P J D， Probert M J， et al. First-principles simulation：ideas， illustrations and the CASTEPcode[J]. Journal of Physics： Condensed Matter， 2002（11）：2717-2744.

[18]Jauch W， Schultz A J， Heger G. Single-crystal time-of-flight neutron diffraction of Cr3Si and MnF2 comparison with monochromatic-beam techniques[J]. Journal of Applied Crystallography， 1987（2）：117-119.

[19] Ren B ， Lu D H ， Zhou R ， et al. First principles study of stability， mechanical， and electronic properties of chromium silicides[J]. Chinese Physics B， 2018（10）：107102.

[20] Li Y ， Gao Y ， Xiao B ， et al. Theoretical study on the stability，elasticity，hardness and electronic structures of W–C binary compounds[J]. Journal of Alloys and Compounds， 2010（1）：0-37.

[21] Bei H， George E P， Pharr G M. Elastic constants of single crystal CrSi and Cr–CrSi lamellar eutectic composites： a comparison of ultrasonic and nanoindentation measurements[J]. Scripta Materialia，2004（9）：875-879.

[22] Chen S， Chen Y， Yan W et al. Magnetism and Optical Property of Mn-Doped Monolayer CrSi2 by First-Principle Study[J]. Journal of Superconductivity and Novel Magnetism， 2017（9）：2759-2765.

[23] Pugh S F. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals[J]. Philosophical Magazine， 2009（367）：823-843.