基于因子分析和三次曲线回归模型的江西GDP预测及政策建议

熊云 林太鹤

摘要：基于对1999-2017年江西GDP及影响因素进行因子分析的基础上，建立了以江西GDP为被解释变量，其他影响因素为解释变量的三次曲线回归模型。运用因子分析法对影响江西GDP的主要因素进行了降维处理，消除了由于变量过多而导致的多重共线性影响，同时得到反映不同年份的综合因子值。考虑到2009年江西受全球金融危机的影响GDP增速缓慢的异常值出现，将综合因子值与时间的关系先作为一个整体研究，然后分成2个时间段分别研究，分别求出不同情况下综合因子值，并在此基础上构建了基于三次曲线回归的江西GDP预测模型。研究结果表明，以2009-2017年作为一个时间段得到的综合因子值预测的数据误差相对较小。同时，针对研究中发现影响江西GDP的各因素存在发展不均衡的问题，本文给出了具体的政策建议。

关键词：因子分析;三次曲线回归模型;江西GDP;预测

1 因子分析的含义及模型

因子分析是通过研究多个变量间相关矩阵（或协方差矩阵）的内部依赖关系，找出综合所有变量主要信息的少数几个随机变量，而这几个随机变量不能直接测量[3]。其目的就是把描述个案的变量空间的维度降低了，用较少的相互独立的因子代替原有变量去分析整个问题。

因子分析的思想可用数学模型来表示，其矩阵的形式[4]为：。其中，X=（，，…，）为原有变量;F=（，，…，;<）为因子，也称公因子;A=（;=1，2，…，;=1，2，…，）为因子载荷矩阵;为特殊因子，表示了原有变量不能被因子解释的部分，其均值为0。

2 实证研究

2.1指标的选取与描述

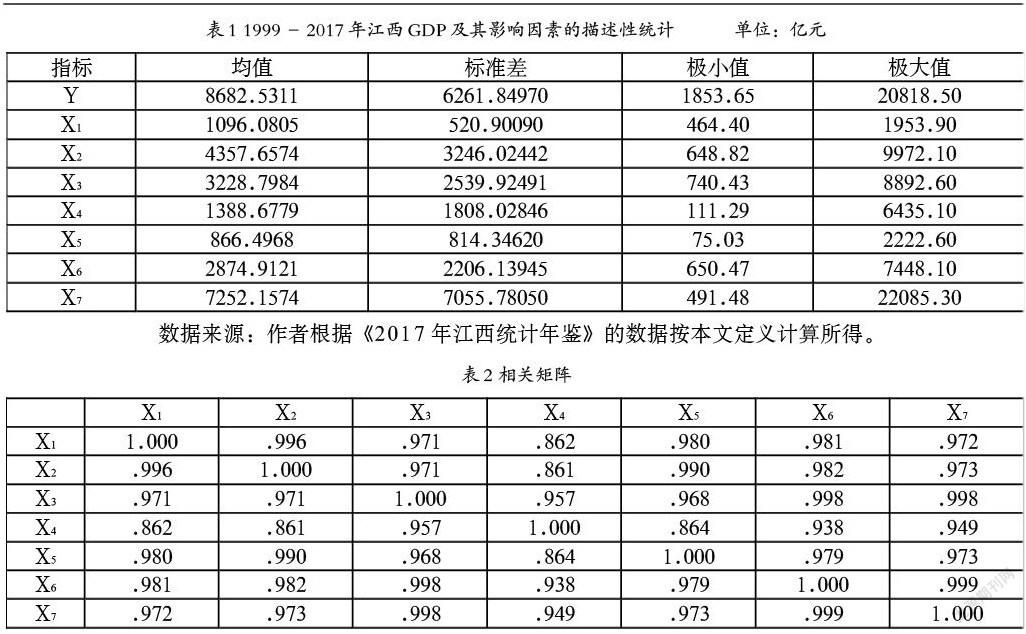
GDP是度量一国或地区经济活动最具综合性的指标，其反映的是一个国家或地区在某一给定的时期内运用生产要素所生产出来的全部最终产品和劳务的市场价值的总和[5]。政策制定者可使用GDP数据监测经济活动的短期波动及长期趋势。然而影响GDP的因素众多，且各因素之间具有程度不一的相关性，本文为全面监测及准确预测江西GDP的发展，选取第一产业总产值（X1）、第二产业总产值（X2）、第三产业总产值（X3）、旅游总收入（X4）、出口总额（X5）、社会消费品零售总额（X6）、全社会固定资产投资总额（X7）等7个经济指标作为江西GDP影响因素。采用1999-2017年江西GDP及相关影响因素数据进行实证研究。1999-2017年江西GDP及其影响因素的描述性统计和相关分析如表1和表2所示。

根据表1的描述性统计分析结果可知，江西GDP历年均值为8682.5311亿元，标准差为6261.84970亿元，发展较快;但其影响因素的第一产业总产值的均值不高，标志变动度最小，可见第一产业发展较为稳定，但对GDP的贡献不大;出口额均值最低，标志变动度仅次于第一产业，出口业发展缓慢;旅游收入的均值略高于第一产业，其标志变动度也偏低，说明江西旅游业还有待进一步开发;而全社会固定资产投资总额的均值和标志变动度在所有因素中最高，发展较快。

根据表2的相关性分析结果可知，自变量之间存在高度线性相关，若直接利用回归模型分析可能会出现多重共线性问题，造成部分回归系数不显著，因此本文利用因子分析中的主成分分析法消除变量间的多重共线性问题，使得解释变量在降低维度的同时消除多重共线性。

2.2 因子分析结果

2.2.1 KMO和Bartlett球形度检验

对样本进行的KMO和Bartlett的球形度检验中，KMO值越接近1，说明变量间的相关性越强，原有变量越适合做因子分析。同时，Bartlett球形度检验对应的概率P值若小于给定的显著性水平，则应拒绝原假设，认为相关系数矩阵不太可能是单位矩阵，原有变量适合采用因子分析。

表3显示了对江西GDP影响因素进行因子分析适用性检验的结果。Bartlett球形度检验的统计量为499.936，相应的概率P为0.000，小于0.05的显著性水平，认为相关系数矩阵和单位矩阵有显著性差异，适合采用因子分析。同时，KMO值为0.808，根据Kaiser给出的KMO度量标准可知，原有变量适合做因子分析。

2.2.2 因子分析共同度

表4“初始”列是因子分析初始解下的變量共同度，表明对原有7个变量如果采用主成分分析法提取所有7个特征根，原有变量的所有方差均可被解释，变量的共同度均为1。“提取”列是按要求提取特征根时的共同度，由表4可知，所有变量的绝大部分信息（全部都大于87%）可被因子解释，变量信息丢失较少，因此，本次因子分析提取的总体效果较为理想。

2.2.3 因子分析的总方差解释

表5描述了因子初始解情况和因子的抽取情况。表中显示只抽取了1个公因子，其特征根值为6.764，解释了原有7个变量总方差的96.632%，从比例上来看是较好的保留了原有变量的信息，因此公因子的提取较为理想。

2.2.4因子载荷矩阵

通过载荷系数大小可以分析不同公因子所反映的主要指标的区别，如表6所示。从结果来看，公因子1在7个指标上的载荷值都很大，故可作为综合因子值看待。

2.2.5 因子得分系数

根据表7可以写出因子得分系数：

2.3 曲线估计结果

从历年江西GDP值可知其呈递增趋势，但结合实际意义，江西GDP不可能无限膨胀下去，其会受到经济基础、人口增长、资源、科技、环境等客观条件的制约。由图1也可初步判断综合因子值与江西GDP二者存在曲线延伸趋势，于是利用三次曲线回归模型预测江西GDP。三次曲线回归模型的曲线大致呈现出由低向高地变动，而后又出现下降再上升的变动趋势。运用该模型分析的目的是使变动趋势曲线与观察期的资料数据变动趋势相适应，更好地反映预测变化的客观实际。

绘制综合因子变量FAC1-1的时间序列图，如图2所示。02757063-5DE6-40F0-A09E-535A2B7CF61B

由图2可见，1999-2017年间综合因子值总体呈上升趋势，但在2009年时出现异常现象，在江西GDP趋于平稳上升增长的途中却呈现增长缓慢局面。由表1数据可知，1999-2008年江西GDP总体呈平稳上升且增长速度加快的趋势，但2009年与2008年相比，江西GDP增长速度明显较缓慢，2010年以后持续增长且增长速度与2010年之前相比是稳而较快，这是因为2009年受全球金融危机的影响经济低迷，江西GDP增长较为缓慢。为了减少误差，将综合因子变量FAC1-1的时间序列图首先作为一个时间段来研究，即1999-2017年共19年的数据进行研究，然后将1999-2017年分为1999-2008年和2009-2017年两个时间段分别研究。

1999-2017年作为两个时间段分别进行研究，得到1999-2008年综合因子时间序列图，如图3所示。

2009-2017年综合因子时间序列图如图4所示。

为便于观察比较，将1999-2017年的江西GDP实际数据与拟合数据的折线图绘制在同一个坐标系中，如图5所示。

为便于观察比较，将1999-2008年的江西GDP实际数据与拟合数据的折线图绘制在同一個坐标系中，如图6所示。

为便于观察比较，将2009-2017年的江西GDP实际数据与拟合数据的折线图绘制在同一个坐标系中，如图7所示。

通过以上分析可知，2009-2017年作为一个时间段，三次曲线回归模型的估计值与实际值偏差较小，拟合效果较好，能够基本满足江西GDP预测的需求。

3 结语

研究可知，三大产业中，第一产业发展虽较为稳定，但作为农业大省发展慢，对GDP的贡献不大，因此农业问题必须得到高度重视，保护好耕地资源，大力推进高标准农田建设，合理规划现有资源，利用高科技手段，寻找新路径，加快农业现代化建设，建立可持续的生态型农业，巩固江西农业大省的地位，提高农业贡献度。另，作为内陆省份，江西出口业发展缓慢，一方面应采取积极有效措施创造良好的出口环境，另一方面应充分利用生态优势，大力发展绿色（有机）农产品出口，同时在稳定和扩大传统市场的前提下，应积极开拓新兴市场，优化出口市场结构，有效化解贸易壁垒风险。同样，鉴于江西旅游资源的丰富多样性，江西旅游业发展潜力大，为此我们应突出江西旅游业奇特山水、红色摇篮、陶瓷艺术等特色，同时大力开发其他有价值的旅游资源，合理规划旅游业发展，展开旅游生产力布局，塑造好江西旅游业的整体形象，增强旅游产业的核心竞争力，使之成为江西省新的经济支柱。

参考文献

[1]刘敏，李岚.基于两步运算的河北省“十二五”时期GDP预测[J].统计与管理，2010（4）：78-80.

[2]李凯，张涛.上海市2017-2020年GDP预测研究——基于改进的GM（1，1）模型[J].华东经济管理，2017（10）：11-15.02757063-5DE6-40F0-A09E-535A2B7CF61B