变式教学 变出精彩

李艳玲

【摘  要】2017年秋，天津进入了高考招生制度综合改革的实验阶段，开始了新一轮的课程改革。为了更好地适应改革发展的需要，培养学生的核心素养，我校对高一年级的课程进行了调整，在高一年级就开启了高中阶段所涉及的所有科目，包括语数英三门高考学科，物、化、生、史、地、政可以自主“6选3”的等级考科目，信息、通用、音乐、美术、体育等合格考科目，以及校本、生涯、班会、社团等学校特色课程。

【关键词】变式;教学

作为一名合格的教师，不仅要在教学过程中实现立德树人的要求，落实“四基”，培养“四能”，还要促进学生的数学学科核心素养的形成与发展，任务艰巨。为了能够更好地迎接这前所未有的挑战，教师需要深入挖掘数学学科的育人价值，优化课堂教学，提高教学效率。而变式教学能够加深学生对数学知识的理解，强化思维训练，从而优化学生的知识结构，提高教学效率，培养数学核心素养，是数学教学的优选策略。

目前的高考命题越来越重视对基础知识的考察，命题的方向越来越注重“源于课本，又高于课本”，题目具有层次性，它不是课本简简单单的重复，而是以课本为依托，通过题目的变式得到的。

一题多变的教学方法，可以使学生充分理解数学知识的本质，掌握数学基本方法的规律性，加深对数学原理的掌握能力。深入挖掘变式题的本质，总结出具有普遍性的规律，可以使学生的知识框架得以充实和丰富，学生的思维能力得到锻炼。因此，变式教学是高中数学教学的优选教学策略。

一、变式教学可以抛弃“题海战术”，减轻学生负担，落实“四基”，实现高效课堂

题海战术的效率低，从根本上讲，原因在于题海战术不能真正拓展学生的思维，只会使学生照搬思路、模仿解题，根本没有形成真正的能力。变式教学不是简简单单地进行题海战术，而是突出练习题中要表达的变异的数学本质，将知识点多角度、全方位、分层次地解析，有助于学生对知识的理解和掌握。

这一点在学习人教A版必修1第一章1.1集合的内容当中有很好的体现。集合是学生进入高中之后的第一课，比较抽象，不易理解，尤其是有关空集的分类讨论，是学生的一个难点，也是易错点。但是通过设计适当的变式题，则可以帮助学生整理题目的本质，突破难点。

例：已知集合[A=x-2≤x≤5]，集合[B=xm≤x≤m+4]，若[B⊆A]，求实数m的取值范围。变式1：已知集合[A=x-2<x<5]，集合[B=xm≤x≤m+4]，若[B⊆A]，求实数m的取值范围。

变式2：已知集合[A=x-2≤x≤5]，集合[B=xm+1≤x≤2m-1]，若[B⊆A]，求实数m的取值范围。

变式3：已知集合[A=x-2≤x≤5]，集合[B=xm+1≤x≤2m-1]，若[CRA⊆CRB]，求实数m的取值范围。

变式4：已知集合[A=x-2≤x≤5]，集合[B=xm+1≤x≤2m-1]，若[B⊂A]，求实数m的取值范围。

当然，在学习了1.2函数及其表示中区间的内容后，还可以引入如下变式：变式5：已知集合[A=x-2≤x≤5]，区间[B=m+1，2m-1]，若[B⊆A]，求实数m的取值范围。

题目的原型是为了考查集合间的基本关系，设计变式1的主要目的在于考查等号成立的条件;变式2的主要目的在于原型中的集合B不可能为空集，而变式2中的集合B则有可能为空集，需要进行分类讨论;变式3是为了进一步巩固变式2的成果，并进一步补充补集运算的练习;变式4则是为了让学生明确子集与真子集的区别，也是整个变式的过程中学生最容易出现思维误区的地方;变式5的作用则在于让学生明确集合与区间的区别与联系，进一步巩固学习成果。

通过以上例题及其变式，我们可以发现，虽然变式之后的结果有所变化，但是解决问题的基本思想方法和解题策略并没有改变。因此，变式教学是有效提高学习质量和效率的教学策略。

二、变式教学有利于激发学生的学习兴趣，提高学习热情，培养“四能”，促进学生数学核心素养的形成和发展

变式教学通过改变知识的非本质特征，促使学生不断思考，探索知识最本质的属性，一题多变给学生以新鲜感，不断变换的形式及内容，不仅开阔了学生的视野，还唤起了学生的好奇心和求知欲，从而产生主动参与的动力，保持其参与教学活动的兴趣和热情。随着周期性的加入，高中阶段所要研究的函数基本性质就都学习过了，可是在所有性质综合之后，很多学生会对函数的周期性和对称性的公式发生混淆，由此可以引入如下变式，以便学生区分、掌握。通过变式教学，学生掌握了三角函数的周期性公式，还掌握了函数的周期性和对称性的基本公式，而且在不断变化的形式中进行对比，加深了学生对知识的理解和掌握。一些数学能力较强的同学还能够根据以上内容，自行进行变式改编，衍生出类似的公式，做到了知识的融会贯通。

三、变式教学可以提高学生灵活运用知识的能力，锻炼发散思维，从而全面有效地提升学生数学学科核心素养

变式教学不仅仅是一题多变，一题多解也是变式教学中非常重要的一部分。在一题多解的教学的过程中，当学生较好地掌握了一般方法后，教师要注意诱导学生离开原有的思维轨道，从多角度、多方面地思考问题，进行思维变通。当学生思维闭塞时，教师要善于调度原型帮助学生接通有关知识和解题经验的联系，产生多种解决问题的设想。

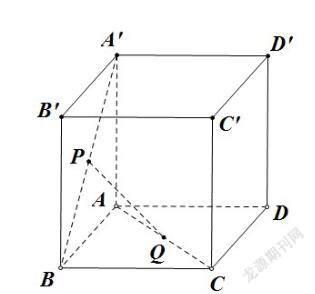
例：如图所示，已知P、Q是正方体[ABCD-ABCD]的面[ABBA]和面[ABCD]的中心，证明：PQ//平面[BCCD]。

在学习了必修2中的立体几何部分内容之后，可以利用几何法解决上面的问题。

方法一：证明PQ//A[′D];

方法二：取[BB′]的中点E，[BC′]的中点F，连接PE，FQ，EF，证明PQ//EF;

方法三：证明PQ//[B′C];

方法四：取AB的中点G，证明平面PGQ//平面[BCC′B]。在学习了选修2-1第三章空间向量与立体几何部分之后，也可以用向量法解决上面的问题。

方法五：利用向量[PQ=12（BB+][BC）];

方法六：建立空间直角坐标系，证明[AB⊥PQ]，其中[AB]为平面[BCC′B]的法向量.

这里从几何方法、空间向量两个角度给出了此题的六种思考方法。可以从不同的角度来解决问题，提高了学生灵活运用知识的能力，锻炼了学生的思维能力，培养了学生的逻辑推理、直观想象、数学运算等能力，从而全面有效地提升学生数学学科核心素养。变式教学使学生在学习时不只是停留于事物的表象，有助于学生拓宽视野、加深对重要概念和重要技能的理解、消化，從而突破课堂教学过程中的重点、难点，提高课堂教学的效益，培养学生从多角度地认识问题的思维习惯，激励他们创新、探究能力的发展。综上所述，教师要有目的、有意识地引导学生从“变”的现象中发现“不变”的本质，从“不变”的本质中探究“变”的规律，帮助学生将所学的知识点融会贯通，从而让学生在无穷的变化中领略数学的魅力，体会到学习数学的乐趣。

（责任编辑  范娱艳）