监利水文站水位流量关系单值化方法初探
黄烈敏 徐清涛 胡家彬


摘要:受洞庭湖顶托、河段冲淤、洪水涨落等多因素综合影响,监利水文站水位流量关系通常呈复杂的绳套关系。各因素在年际、年内各场次洪水中存在差异,且相互之间亦有影响,难以有效利用单值化进行分析,使得水文测验、河道行洪能力分析、洪水调度与预报等工作的开展较为困难。采用监利水文站2010~2017年的实测水位、流量资料,通过落差指数法校正,并结合水位-过水面积关系进行分析,综合确定以2016年的水位-校正流量关系及水位-过水面积关系作为参照基准,对各年份的河段冲淤影响进行校正。结果表明,对于发生整体趋势性冲淤而年内随机性冲淤不大的年份,其水位-校正流量单值化关系得到较好地改善,具有较高的定线精度。
关键词:水位流量关系;单值化;河段冲淤;流量校正;监利水文站
中图法分类号:P332文献标志码:ADOI:10.15974/j.cnki.slsdkb.2019.11.001
长江中下游洪水峰高、量大、历时长,且为洪水滞蓄宣泄和泥沙堆积的场所,一直以来是长江流域洪灾多发区[1]。监利水文站(以下简称“监利站”)地处长江中下游的下荆江河段,为长江中下游重要的防汛测报站,研究其控制断面的水位流量关系,对下荆江河道行洪能力分析、三峡水库洪水调度、洪水预报以及防洪规划等具有非常重要的意义[2]。然而受诸多因素的影响,天然河流水位流量关系通常呈不稳定的形态,即水位与流量呈多值关系,这种关系不仅给测站汛期流量测验带来较大的工作量,而且给洪水预报、水文计算带来不便。因此对影响监利站水位流量单值化关系的因素及其改正方法进行探讨与研究具有重要的意义。
1 监利站概况
监利站始建于1934年,新中国成立前该站仅用于观测水位,名为监利(城南)。1950年8月水位站改为水文站,更名为监利(一)站,并于2010年1月迁至监利鄢铺汽渡码头上游约1 300 m处,期间因河段冲淤及洲滩变化断面历经几次迁移,现为监利(二)站。该站测验断面上、下游各有约500 m长顺直河段,河槽偏“V”型,左浅右深,中高水河槽宽约1 100~1 300 m,下游约5.5 km有乌龟洲。洞庭湖在下游约95 km处与长江交汇,使该站水位流量关系受回水顶托影响明显。河床由中细沙组成,冲淤剧烈,年内、年际变化大。河段示意如图1所示。
2 水位流量关系特征
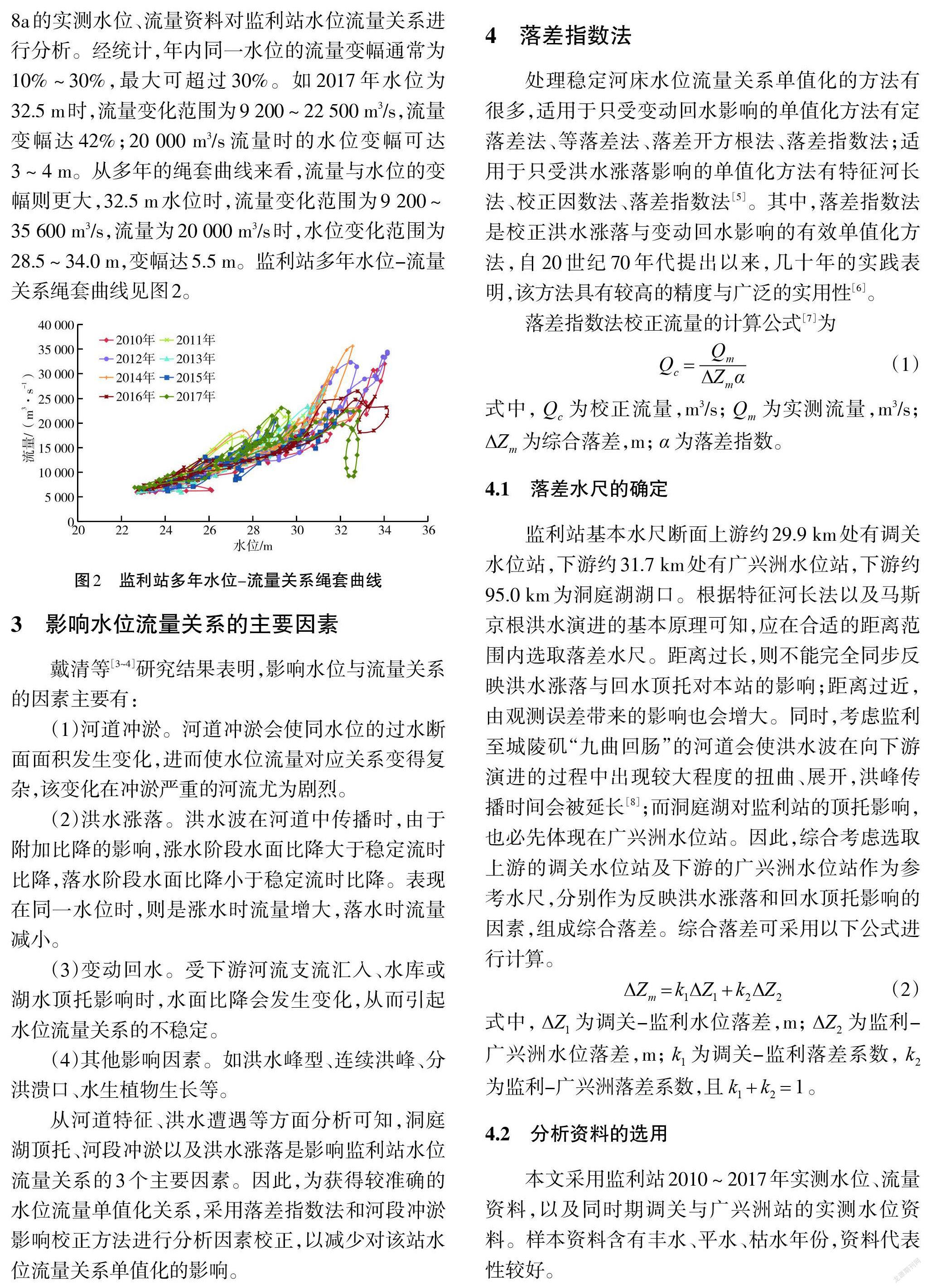
监利站水位流量关系受变动回水、河道冲淤、洪水涨落等因素共同影响,实测水位流量连时序线呈极其复杂的绳套曲线关系,年内和年际间同条件下,水位流量变幅巨大。采用监利站2010~2017年8a的实测水位、流量资料对监利站水位流量关系进行分析。经统计,年内同一水位的流量变幅通常为10%~30%,最大可超过30%。如2017年水位为32.5 m时,流量变化范围为9 200~22 500 m3/s,流量变幅达42%;20 000 m3/s流量时的水位变幅可达3~4 m。从多年的绳套曲线来看,流量与水位的变幅则更大,32.5 m水位时,流量变化范围为9 200~35 600 m3/s,流量为20 000 m3/s时,水位变化范围为28.5~34.0 m,变幅达5.5 m。监利站多年水位-流量关系绳套曲线见图2。
3 影响水位流量关系的主要因素
戴清等[3~4]研究结果表明,影响水位与流量关系的因素主要有:
(1)河道冲淤。河道冲淤会使同水位的过水断面面积发生变化,进而使水位流量对应关系变得复杂,该变化在冲淤严重的河流尤为剧烈。
(2)洪水涨落。洪水波在河道中传播时,由于附加比降的影响,涨水阶段水面比降大于稳定流时比降,落水阶段水面比降小于稳定流时比降。表现在同一水位时,则是涨水时流量增大,落水时流量减小。
(3)变动回水。受下游河流支流汇入、水库或湖水顶托影响时,水面比降会发生变化,从而引起水位流量关系的不稳定。
(4)其他影响因素。如洪水峰型、连续洪峰、分洪溃口、水生植物生长等。
從河道特征、洪水遭遇等方面分析可知,洞庭湖顶托、河段冲淤以及洪水涨落是影响监利站水位流量关系的3个主要因素。因此,为获得较准确的水位流量单值化关系,采用落差指数法和河段冲淤影响校正方法进行分析因素校正,以减少对该站水位流量关系单值化的影响。
4 落差指数法
处理稳定河床水位流量关系单值化的方法有很多,适用于只受变动回水影响的单值化方法有定落差法、等落差法、落差开方根法、落差指数法;适用于只受洪水涨落影响的单值化方法有特征河长法、校正因数法、落差指数法[5]。其中,落差指数法是校正洪水涨落与变动回水影响的有效单值化方法,自20世纪70年代提出以来,几十年的实践表明,该方法具有较高的精度与广泛的实用性[6]。
4.2 分析资料的选用
本文采用监利站2010~2017年实测水位、流量资料,以及同时期调关与广兴洲站的实测水位资料。样本资料含有丰水、平水、枯水年份,资料代表性较好。
4.3 落差系数和落差指数的优选
(1)落差指数[α]初值选取0.5,计算[k1]以0.05为步长,从0~1不同落差系数组合下的校正流量[Qc],采用三次方多项式对水位-校正流量数据点进行拟合(方次太低,不易达到精度要求;方次越高,拟合程度越好,但易出现拟合线的异常波动,甚至反曲的现象;因此选用三次方较为适宜)。优选拟合相关度最好的落差系数确定为最终落差系数组合。
(2)按0.01的步长,在[0,1]范围内,进一步调整落差指数[α]的取值。通过试错法优选水位-校正流量数据点相关度最好的[α]值。
按上述过程,各年份优选得到的落差系数、落差指数以及拟合精度指标统计如表1所示,各年份水位-校正流量关系见图3。
4.4 落差指数法校正效果的分析
通过对表1中参数优选与成果精度结果以及图3中各年水位与校正流量关系的分析,结果如下。
(1)经落差指数法校正后,监利站各年实测水位-流量关系点由散乱明显变得集中且成带状分布,三次方多项式曲线能较好地拟合水位-校正流量关系,点距无明显偏离,相关度R2达到0.97以上,符号检验、适线检验、偏离数值检验均能满足SL 247-2012《水文资料整编规范》[9](以下简称“《规范》”)要求。
(2)从各年优选得到的落差系数k1均为零可知,上游调关站的落差对监利站进行落差指数法单值化校正的影响极小。其原因可能是监利站处于长江中游,属平原型河流,水面比降通常较小,洪水涨落速率远不及山区河流,因此上游站落差在综合落差中并不能灵敏地反映上游洪水涨落对本站的影响;另一方面,落差系数k2为1,表明多数情况下,洞庭湖顶托的影响比洪水涨落的影响大,且为水位-流量关系单值化的主要影响因素。若选用该站水位涨落速率作为参数,通过校正因素法改正上游洪水涨落的影响可能会使单值化效果更好。
(3)由于存在河段冲淤的影响,落差指数[α]各年优选值不同,取值范围为0.53~0.94,变化范围较大;随机不确定度与最大相对误差,除2013年与2016年较低外,在其余年份两者误差均大于8%和13%,相对误差大于10%的点据数仍较多。
(4)落差指数法在一定程度上能有效地对回水顶托与洪水涨落因素的影响进行校正,但为了得到更理想的水位-流量单值化关系,需在此基础上进一步减小河段冲淤因素的影响。
5 河段冲淤影响的校正
5.1 水位-过水面积关系变化分析
不稳定河床冲淤变化是影响水位-流量关系单值化的因素之一,水位与过水面积关系的变化可直观反映河段冲淤的影响。监利站2010~2017年流量测验水位与实测过水面积关系见图4。
从图4可看出,监利站测流断面各年水位-过水面积关系较水位-流量关系相关度更高;拟合曲线的偏移情况可反映测流断面年际间冲淤变化情况,点据偏离拟合曲線的程度可反映年内场次洪水断面冲淤变化的剧烈程度。
(1)2011年、2014年较前一年份断面整体略有冲深,相同过水面积下,水位平均降低约0.2 m;2017年较上一年整体有较大冲深,相同过水面积下,水位平均下降约0.6 m。
(2)2012年较2011年的断面中高水部位略有淤积,低水部位略有冲刷;而2013年中高水部位有小幅冲深,低水部位略有淤积;2015年较2014年中低水部位有小幅冲深,高水部位基本无变化;2015~2016年水位-面积关系总体无变化。
(3)2010~2017年,监利测流断面总体平均降低了约1.1 m。
(4)2010年和2012年,点据偏离拟合曲线幅度较大,即相关度R2相对较低。年内场次洪水引起的断面冲淤变化较剧烈,同过水面积下,水位变幅最大分别为1.6 m与1.9 m左右。其余年份水位-面积关系曲线拟合相关度较高,点据相对集中,2016年相关度R2最高,为0.997 5。
总体来看,监利站测流断面的水位-过水面积关系在年际间、年内各场次洪水间常会发生改变,不同年份变化程度不同,处于不断动态变化过程中。
5.2 河段冲淤影响校正的参照基准
综合前文落差指数法校正以及水位-过水面积关系变化的分析可知,由于洞庭湖顶托、河段冲淤等因素在年际、年内各场次洪水中影响存在差异,且因素之间亦有相互影响,使得水位流量关系通常缺乏可比性。河段冲淤的变化会使过水断面发生变化(即水位-过水面积关系变化),同时也会对河道比降带来调整(即落差的改变)。洞庭湖顶托的强弱亦会造成水面比降的改变(即落差的改变)以及河段流速的变化(引起河段冲淤特性变化)。因此,在复杂条件下,为使水位流量关系具有可比性,须确定一个具有一定代表性和定线精度的水位-校正流量关系以及水位-过水面积关系作为参照基准。
由于2016年的水位-过水面积关系相关度最高,且年内测流最高水位为34.13 m,能较好地涵盖监利站近年水位变化范围;同时在落差指数法校正结果中,2016年水位-校正流量关系最好,随机不确定度为5.60%,最大相对误差不超过10%,因此综合确定以2016年的水位-校正流量关系及水位-过水面积关系为参照基准。
5.3 河段冲淤影响校正步骤
对各年份的河段冲淤因素影响校正按以下步骤进行。
(1)将各流量测次实测的过水面积A代入2016年率定的Z-A相关关系式中,可得到相应的参照水位[Z']。
(2)将参照水位[Z']代入2016年率定的Z-Qc相关关系式中,可得到对应的校正流量Qc。
(3)再由实测流量Q、参照水位[Z']以及校正流量Qc,通过2016年的落差指数公式反算,可得到相应的参照落差[?Z']。
(4)最后利用实测水位Z、实测流量Q以及参照落差[?Z'],再次进行落差指数法单值化处理,从而得到该年河段冲淤影响校正后的水位-校正流量关系。
5.4 校正效果分析
监利站河段冲淤影响校正前后水位-校正流量关系精度指标统计及对比结果见表2。各年河段冲淤影响校正后水位-校正流量关系见图5。
通过校正效果分析可知:
(1)经河段冲淤校正后,除2010年与2012年外,其余各年监利站水位-校正流量单值化关系有明显改善,随机不确定度均校正至6.4%以内,最大相对误差降低至10%以内,已达到《规范》一类精度水文站采用单一曲线的随机不确定度大于8%的要求[9]。
(2)落差指数[α]取值范围更集中,水位-校正流量单值化关系有明显改善的6 a中有5 a为0.60。
(3)如将三峡水库清水下泄导致的河段断面总体性冲淤作为趋势性冲淤,而场次洪水及洞庭湖顶托影响产生的河段冲淤作为随机性冲淤,则发现:①有整体趋势性冲淤而年内随机性冲淤不大的年份,如2011,2013,2014,2015年及2017年水位-校正流量关系得到较大改善;②随机性冲淤较大的年份,如2010年与2012年,由于年内各场次洪水引起的过水面积与比降变化差异较大,经2016年参照基准得到的参照水位与参照落差仍不能有效改善水位-校正流量关系。
6 结 论
本文从监利站水位流量关系的影响因素出发,通过落差指数法[10]对洞庭湖顶托及洪水涨落影响进行校正,得到较好的水位-校正流量关系,并结合水位-过水面积的变化分析,综合确定以2016年的水位-校正流量关系及水位-过水面积关系为参照基准,进而对各年份的河段冲淤影响进行校正。通过以上分析与处理,可以得到以下结论。
(1)落差指数法在一定程度上能有效地对监利站回水顶托影响进行校正,使散乱的水位流量关系点明显变得集中。上游站落差在综合落差中不能灵敏地反映上游洪水涨落对本站的影响;在大多数情况下,洞庭湖顶托是水位流量关系的主要影响因素。
(2)监利站测流断面的水位-过水面积关系在年际间、年内各场次洪水间常发生改变,不同年份变化程度不同,2010~2017年断面总体冲深,同过水面积下,水位平均下降约1.1 m;2010年和2012年,场次洪水引起的断面冲淤变化较剧烈,同过水面积下,水位变幅最大可分别达到1.6 m与1.9 m左右。
(3)经按2016年参照基准进行河段冲淤校正,发生整体趋势性冲淤而年内随机性冲淤不大的年份,其水位-校正流量单值化关系得到较大改善,达到《规范》中一类精度水文站定线的要求。
参考文献:
[1] 万凤鸣,龙立华,张悦. 单值化处理长江中游主要断面水位流量关系研究[J]. 长江科学院院报,2012,29(12):5-9,33.
[2] 李振林,唐从胜. 洞庭湖顶托对下荆江泄洪量的影响[J]. 水文,2000,20(6):27-28,31.
[3] 戴清,韩其为,毛继新. 长江中游散乱水位流量关系单值化处理研究[J]. 泥沙研究,1999(3):63-68.
[4] 郭希望,陈剑池,邹宁,等. 长江中下游主要水文站水位流量关系研究[J]. 人民长江,2006,37(9):68-71.
[5] 长江水利委员会水文局. 水位流量关系单值化处理应用技术成果汇编[R]. 武汉:长江水利委员会水文局,1983.
[6] 葛维亚,罗学棋,唐佩文. 稳定河床水位流量关系单值化处理方法及其应用[J]. 人民长江,1981(2):1-12.
[7] 吴世勇,刘晓琴,彭艳明. 沙市二郎矶站水位流量关系单值化分析研究[J]. 人民长江,2010,41(21):42-44,84.
[8] 黄诚良. 落差指数法在水位流量关系单值化处理中的应用[J]. 长江工程职业技术学院学报,2010,27(2):52-54.
[9] SL 247-2012水文资料整编规范[S].
[10] 万凤鸣,龙立华. 落差指数法在长江中游螺山站水位流量关系研究中的应用[J]. 科技创新導报,2013(24):248,250.
(编辑:李晓濛)

