基于双向流固耦合的流线型箱梁断面颤振分析

摘要：文章以大型有限元分析软件Ansys - Fluent为计算平台，基于计算流体动力学方法，采用大涡模拟湍流模型，求解不可压缩流体N-S方程，对在不同风速下苏通大桥的流线型箱梁断面的振动响应进行了CFD数值模拟研究。研究结果表明：当来流风速处于145 m/s附近时，发生了“软颤振”现象;当风速超过147 m/s时，发生了明显的“颤振”现象，说明该流固耦合计算方法所得出的数值模拟结果与已有文献试验结果吻合较好。

关键词：箱梁断面;颤振;动网格;UDF;双向流固耦合

中图分类号：U448. 21+3文献标识码：A

DOI： 10.1 3282/j. cnki. wccst. 201 9. 12. 026

文章编号：1673 - 4874（2019）12 - 0095 - 05

0引言

颤振是一种典型的横风向发散性自激振动现象，当气流流经流线型断面时，气流和结构相互耦合作用。当来流风速超过某一定值时，振动的桥梁结构会在垂直于气流的方向发生非常显著的大幅度振动，其特点是振动的桥梁结构源源不断地从气流中吸收能量，此时结构吸收的能量大于结構阻尼所消耗的能量。随着结构设计和施工水平的提高，现代桥粱结构向柔性、轻质的方向发展，这使得桥梁对风荷载的敏感性大大增强，特别是在施工状态，风致振动问题表现得更为激烈。因此，施工状态下的风致振动问题是桥梁风致作用研究的主要方向。起初，桥梁抗风动力特性研究主要是通过缩尺模型风洞试验进行分析，实验往往受到人力、物力、时间等因素的影响，使得桥梁结构风洞试验研究举步维艰。随着计算机硬件的提升以及计算流体动力学理论的完善，CFD数值模拟逐步取代了风洞试验。

目前，大跨度桥梁的抗风研究主要集中在涡振和抖振，对流线型箱梁断面的颤振研究相对较少。Bleich[1]首次运用理想平板气动自激力理论研究了桥梁扭转颤振的可能性。Tomko[2]对主梁断面颤振导数进行了深入研究，奠定了桥梁颤振分析理论的基础。Frandsen[3]基于任意拉格朗日一欧拉法对弹性支撑于流场中的桥梁断面进行了流固耦合数值模拟研究，并测出了颤振临界风速。Slevam[4-6]等通过有限元方法求解流体瞬态N-S方程以及通过ALE方法实现了桥梁结构流固耦合数值计算模型，最后对其颤振稳定性计算进行了流固耦合数值模拟研究。刘志文[7]通过在Fluent嵌入自定义程序代码UDF，基于Newmark-p法求解结构振动方程，采用两方程模型求解不可压缩Navier -Stokes方程，利用弹簧光顺法及网格重构法搭配使用的动网格技术建立了流固耦合数值计算模型，对桥梁断面进行了风致振动响应计算。李永乐[8]基于CSD和CFD耦合振动分析方法，采用微分方程的数值解法和动网格技术对方柱和平板的颤振进行了数值模拟研究。张瑞琴[9]利用CFX软件对典型翼型断面进行了流固耦合作用下的颤振研究。综上所述，当前的文献基于CFD方法对桥梁断面的颤振研究依然较少。

本文以苏通大桥的流线型箱梁断面为研究对象，采用“刚生运动区域+动网格区域+静网格区域”的动网格策略建立网格，基于Newmark -β法，对计算流体动力学软件Fluent进行二次开发，将求解的结构振动响应编入UDF中，对桥断面风致振动响应进行了流固耦合数值模拟研究。本文数值模拟得到了考虑流固耦合作用时的流场特性，并分析了颤振响应机理。本文数值模拟结果与已有文献的结果吻合较好[10]。

1 箱梁断面流固耦合数值模拟方法

1.1 流体控制方程求解

CFD流体计算为了准确地对湍流流动进行数值模拟，一方面要求计算域的尺寸应该包含湍流中可能出现的最大涡，另外一方面要求网格最小尺寸足以分辨最小涡的运动。然而，就目前的计算机硬件能力而言，能够采用的最小的计算网格的尺度仍然比最小涡的尺度大许多。权衡之下，Fluent求解器中推出了一种比较流行的湍流模型——大涡模拟LES湍流模型，可以通过建立亚格子尺度模型来模拟小尺度涡对大尺度涡运动的影响。

本文CFD数值模拟分析流体计算采用二维大涡模拟湍流模型进行求解不可压缩的Navier - Stokes方程，其控制方程为：

1.2 结构振动控制方程求解

需要注意的是，Ansys - Fluent仅仅是CFD流体计算分析软件，并不能直接对结构的变形进行求解。因此，当我们需要求解结构的振动响应时，就需要编写相应的振动方程的程序。本文通过编写自定义程序代码UDF对Fluent进行二次开发，得到了一种箱梁断面风致振动流固耦合的数值分析方法。此程序还实现了Fluent并行计算，提高了计算效率，并且可以对类似的二维结构断面进行涡振、颤振分析，对其结构安全性具有重要的评估意义。

本文考虑了结构的竖向振动及扭转振动，即对苏通大桥流线型箱梁断面进行了两自由度的流固耦合数值模拟研究。箱梁断面振动控制方程表达式为：

本文是将Newmark -口算法嵌入UDF中求解结构的振动方程，通过Define—CG—Motion指定动网格区域的网格运动位移，进而实现气流与苏通大桥箱梁断面的流固耦合数值模拟方法。

2 工程背景及计算参数

2.1 工程背景

为了检验本文流固耦合数值模拟方法的计算精度，进行了宽高比为10：1的简单桥断面颤振临界风速计算。以苏通大桥为计算背景，该桥为双塔双索面斜拉桥，主桥跨径采用100 m+100 m+ 300 m+1 080m+300 m+100 m+ 100 m，主梁采用的是流线型钢箱梁断面型式，其横截面桥宽41 m，梁高4m。

2.2 计算分析参数

2.2.1 苏通大桥流线型箱梁断面动力特性参数

本文采用大型有限元分析软件Ansys对苏通大桥进行了动力特性分析，得到了竖弯频率及扭转频率，分别为0. 196 Hz、0.565 Hz，如表1所示。

2.2.2边界条件及湍流模型

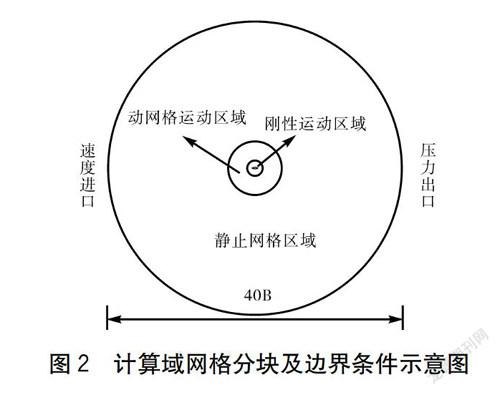
入口采用速度入口边界条件，切向速度为零，湍流强度设为0.5%，湍流黏性比设为2;出口为压力出口边界条件，参考压力为一个大气压。桥梁主梁断面表面为无滑移壁面，整个流域阻塞率为0.3%，满足阻塞率<5%的要求。计算域分块及边界条件如圖2所示。

本文CFD数值模拟计算结合“刚性运动区域+动网格运动区域+静止网格运动区域”的动网格划分策略，箱梁断面壁面处首层网格高度取值为1/4 0008，其中B=41 m。刚性运动区域采用高质量全结构化网格，将箱梁结构壁面随刚生层运动区域一起运动，从而解决了箱梁壁面边界层网格因为变形而出现的网格畸变和负体积等问题，确保了边界层关键部位的网格质量，提高了计算精度。动网格区域采用三角形网格进行划分，在结构振动过程中，这部分网格会进行重新划分，更新网格。为了提高计算效率，最外侧网格采用静止的结构化网格进行划分。

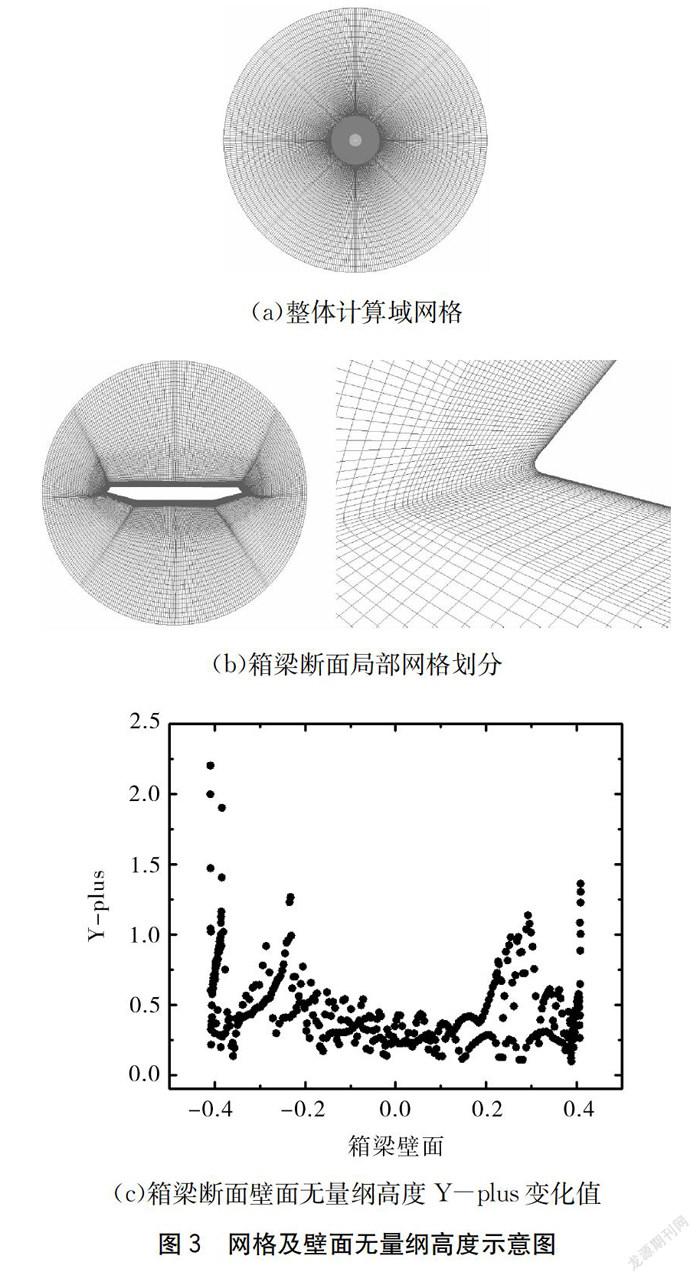
本文湍流模型为大涡模拟LES三维湍流模型，先进行2 000步稳态计算，将稳态结果作为瞬态计算的初场以提高计算效率。为了满足计算结果的精度，壁面网格无量纲高度Y- plus值在1附近。经过网格无关性和时间无关性测试，最终时间步长确定为5×10 s，流体分析二维总网格数量为21万，网格划分及箱梁壁面Y- plus值如图3所示。计算在国家超算高性能计算机群上进行，每个工况申请6个CPU进行并行计算，单工况耗时约为50 CPUs。

3 数值模拟结果及分析

文献M的作者给出了苏通大桥的颤振临界风速为145.5 m/s，为此，本文采用CFD流固耦合数值模拟方法对3个来流风速进行了流固耦合颤振响应研究，分别为144 m/s、146 m/s、147 m/s。Fluent计算过程中，采用了SST k-w、RNG k-e和LES大涡模拟共计三种湍流模型分别对苏通大桥计算了其箱梁断面的三分力系数，选用的时间步长有0.000 1 s、0.000 5 s、0.000 05 s。最后比较得出：LES大涡模拟湍流模型及0.000 5 s的时间步长模拟出的结果和参考文献的结果最为接近。因此，本文的流固耦合数值模拟部分最终采用的是LES大涡模拟湍流模型，数值模拟结果与参考文献的结果相对吻合。

3.1 振动响应分析

下页图4～6为苏通大桥钢箱梁断面的风致振动时程位移随来流风速的变化曲线。当来流风速≤146 m/s时，竖弯振动和扭转振动幅值均很小，竖弯运动和扭转运动均呈现出衰减运动的趋势，最终稳定下来，上下波动特别缓和;当来流风速达到146 m/s时，此时的苏通大桥发生了非常明显的大幅度振动，扭转位移发散，出现了“颤振”现象。经过参考大量的关于颤振的文献发现，当桥梁进入颤振临界状态后，不一定一直呈现出发散性的运动，而是呈现出稳定的大振幅“扭转涡激共振”现象，即“软颤振”现象。比如当来流风速为147 m/s时，出现了“软颤振”现象，即“扭转涡激共振”现象。

3.2 振动机理分析

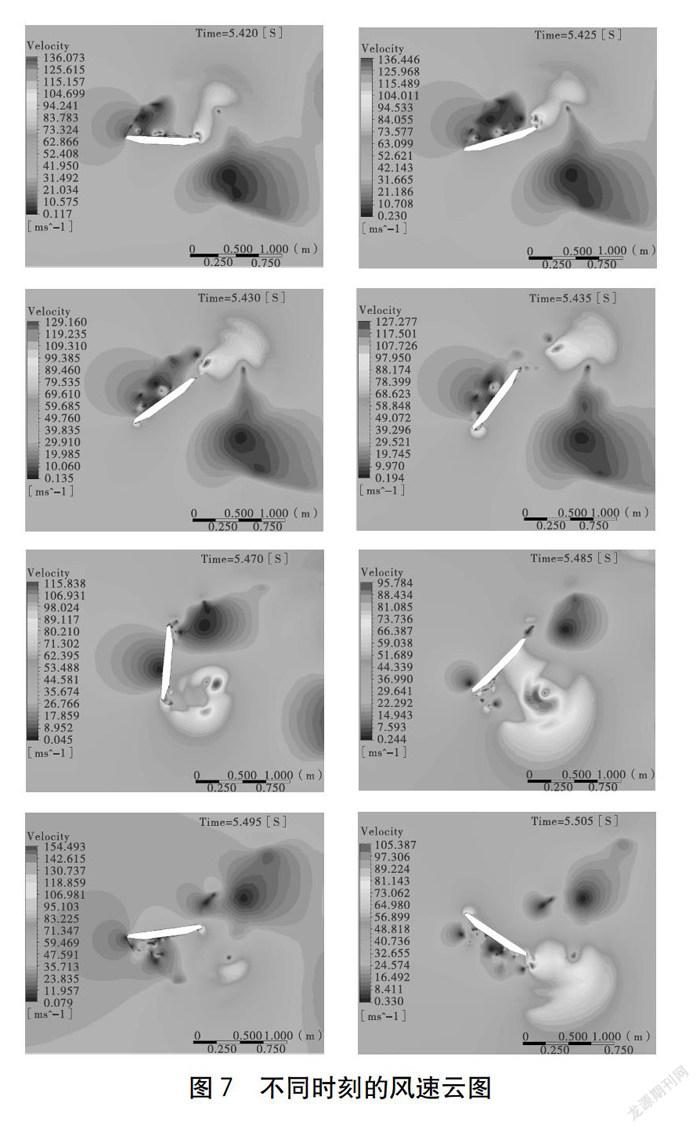
考虑流固耦合效应下的风场不同时刻处的风速云图（如图7所示）。从风速云图可以明显看出：不同时刻的漩涡脱落位置均不一样，漩涡表现得非常激烈，同时夹杂了许多小涡。从这里也侧面反映出苏通大桥在高风速下，发生了大幅度振动。

4 结语

本文基于CFD方法，以苏通大桥的流线型箱梁断面为研究对象，成功模拟了高风速下苏通大桥颤振临界风速，结论如下：

（1）本文在Fluent软件的基础上进行二次开发，结合“刚、生运动区域+动网格区域+静网格区域”的网格划分策略，有效解决了苏通大桥颤振响应计算过程中由于大变形可能产生的网格畸变及负体积等问题。经数值模拟结果与相关文献进行比较，证明了该方法的正确性，此方法可应用于类似结构的流固耦合分析。

（2）本文通过CFD数值模拟分析，得到了苏通大桥的颤振临界风速为146 m/s。

（3）当风速增大到147 m/s时，出现了大幅值稳定的扭转运动，即发生了“软颤振”现象。

参考文献

[1] Bleich F_ Dynamic instability of truss-stiffened suspensionbridges urder wind action[J].Transocticns of the Americanscciety of civil engineers，1949（ 114） ： 1 177-1 222.

[2]Scanlan R H， Tomko J J.Airtoil and Bridge Deck FlutterDerivatives[J]. Journalof the Engineering MechanicsDivision，1971 ， 97（ 6） ：1 717 -1 733.

[3]Frandsen J B.Numerical bridge deck studies using finiteelements Part l： flutter [J]. Journal of Fluids &Structures， 2004，19（ 2） ： 1 71 -191.

[4] Bosch H， Selvam R P. Govindawamy S. Aeroelasticanalysis of bridges using FEM and moving grids[J].Wind & Structures An International Journal， 2002. 5：257 - 266.

[5] Dettmer W， Peri D. A computational framewo rk for f|uid -rigid body interaction： Finite element formulation andapplications [ J ]. Computer Methods in Applied Mechanics and Engineering， 2006 ，195（13 - 1 6） ：1 633 -1 666.

[6]Braun A L， Awruch A M. Finite element simulation of thewind action over bridge sectional modelS： Applicationto the Guama River Bridge（ Par State， Brazil）[J]. FiniteElements in Analysis&Design， 2008， 44（3） ：105 - 122.

[7]刘志文，周帅，陈政清.宽高比为4的矩形断面涡激振动响应数值模拟[J].振动与j中击，2011，30（11）：153 - 156.

[8]李永乐.基于CFD的桥梁涡激振和颤振气弹模拟研究[D].成都：西南交通大学，2013.

[9]张瑞琴，翁建生.基于流固耦合的叶片颤振分析[J].计算机仿真，2011（3）：48- 51.

[10] Rui Zhou， Yaojun Ge， Yongxin Yang， et al. Quasi-3Dfinite element modelling of nonlinear aerodynamic be-haviours of super long-span cable-supported bridges[J].Transactions of the American society of civil engi-neers， 2018（52）：1 011 -1 040.

[11]王林凯，夏飞龙，刘志文，等.基于流固耦合的钢箱梁断面颤振数值模拟[J].公路，2019， 64（7）：108 - 114.

作者简介：黄新章（1976-），工程师，从事国省道日常养护及项目大中修管理工作。