浅谈如何让学生学会数学

陈培贤

在教学过程中，我们常常有这样的困惑，有些学生对于教材上的知识点非常清楚，但为什么做较综合的题目时，会没有思路;当我们跟他们讲解的时候，他们又都能恍然大悟。这说明虽然学生能记住知识点，但对于知识点如何运用，或者是与别的知识点如何结合运用的能力非常地欠缺。这样的学生往往给我们的反馈是这样的：老师，我听懂了！

在这里，我思考一个问题：听懂了一定表示会了吗？事实上并不是，学生在学习过程中，经常会做到一些以前做过的题目，但是很多学生仍然做不出来。究其原因，学生只是当时听懂了而已，并没有对题目进行反思总结，归纳方法，学生对于题目的认知还停留在表层。我们培养的学生不仅仅是听懂而已，更重要的是能够独立思考，根据题目条件，进行知识点的综合运用。让学生学会数学，学会的是数学的思维方法，思维能力。不仅仅是解决一个问题而已。以下我将结合数学学科特点，浅谈如何让学生学会数学。

1.以学生为主体，调动学生的思维

“学而不思则罔，思而不学则殆”，在教学过程中，我们应当给予学生充分地思考时间，要与学生展开互动，交流学生的想法，设置一些相关的问题，引导学生积极思考。而不是直接将题目的解题过程一一闡述出来。很多学生在碰到题目不会的时候，会马上问同学或老师，

有时会急于解决问题，直接讲解解题过程，忽略了调动学生的思维。对于这样的学生，应当先让他讲讲题目的条件是什么，每个条件可以怎么用，和要求的问题有什么联系，解决问题需要什么条件等等，启发学生进行思考，有时在交流过程中，学生就已经会解决问题了。

例如：我们知道方程的解是 X1=1，X2=-3 ，现给出另一个方程，它的解是

很多学生在做这道题的时候，会不假思索地先去括号，再整理求解，虽然能解决问题，但是解法上过于麻烦。这样的学生缺乏观察的意识和能力，或者说是缺少数学思考，想当然地就去解决问题。我们应当培养学生分析条件的能力，寻找解题最优的方法。

2.学会分析条件，探寻条件

大部分学生对于像解方程，不等式这样的题目，都能较好地解决。这些题目有一个特点，那就是解题步骤基本一样，会一个就会一片。但是对于知识点结合的题目，学生往往无从入手，

对于这样的题目，我们应当教会学生分析条件，探寻条件的能力。让学生能够进行知识点的联想，能够分析条件怎么用，所求的问题需要什么条件等等。

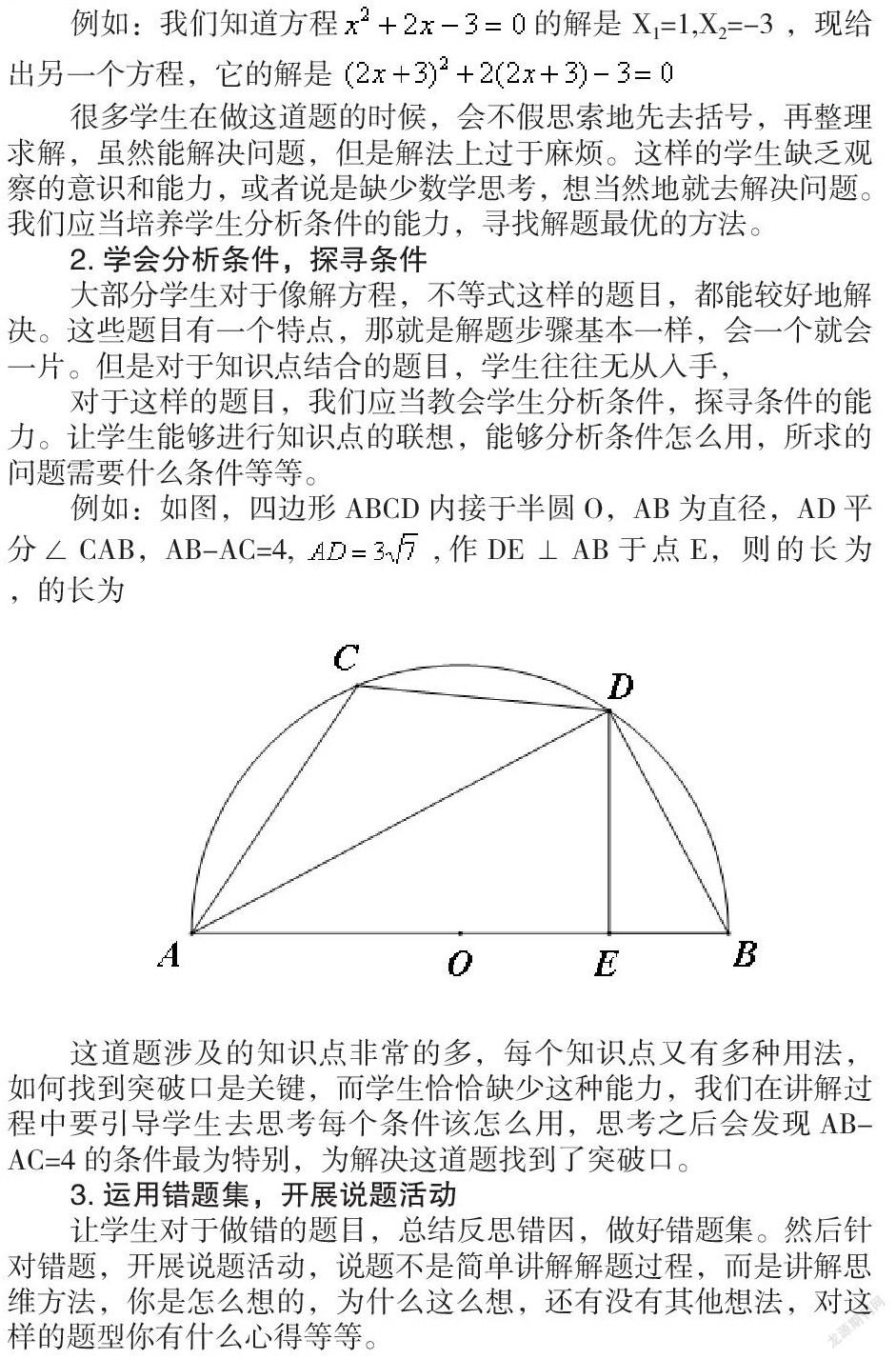
例如：如图，四边形ABCD内接于半圆O，AB为直径，AD平分∠CAB，AB-AC=4，，作DE⊥AB于点E，则的长为     ，的长为

这道题涉及的知识点非常的多，每个知识点又有多种用法，如何找到突破口是关键，而学生恰恰缺少这种能力，我们在讲解过程中要引导学生去思考每个条件该怎么用，思考之后会发现AB-AC=4的条件最为特别，为解决这道题找到了突破口。

3.运用错题集，开展说题活动

让学生对于做错的题目，总结反思错因，做好错题集。然后针对错题，开展说题活动，说题不是简单讲解解题过程，而是讲解思维方法，你是怎么想的，为什么这么想，还有没有其他想法，对这样的题型你有什么心得等等。

例如：已知直线与X轴，Y轴交于A，B，抛物线的顶点为C，连接BC.

（1）求A，B，C的坐标;

（2）试确定线段AB，BC的位置与数量关系，并说明理由;

（3）设点D在直线AB上，点E在X轴上，探索是否存在以CD为腰的等腰Rt△CDE.若存在，请求出所有满足条件的的坐标，若不存在，请说明理由.

对于这题的第（3）问，要让学生讲解共有几种情况，你是根据什么分类的，总结解决此类问题的基本方法是什么。解决完此题，还可以对学生进行变式训练，以检测学生是否真正掌握解决问题的思维方法，而不是仅仅听懂一题而已。

总之，在教学过程中，要让学生学会数学，学会解决问题的思维。课堂教学是一门艺术，我们要让学生从学数学向研究数学转变，发挥学生的主体作用，以提高学生的数学思维能力。