地震前兆指标分析

孙娟

摘 要：针对震前各指标的变化幅度和相应震级，本文使用MATLAB软件建立相关系数分析矩阵模型，得出各指标对地震的敏感程度。同时，运用主成分分析法对相关指标进行综合分析，并以时间序列对综合指标进行数据拟合，得出地震前兆综合指标的变化趋势。

关键词：地震前兆;相关系数分析;主成分分析法

中图分类号：P315.72 文献标识码：A 文章编号：1003-5168（2019）23-0156-03

A Study on the Index of Earthquake Precursors

SUN Juan

（University for Science & Technology Sichuan，Chengdu Sichuan 610000）

Abstract： According to the variation range of the indicators before the earthquake and the corresponding magnitude， this paper used MATLAB software to establish the correlation coefficient analysis matrix model， and obtained the sensitivity of each index to the earthquake. At the same time， the principal component analysis method was used to comprehensively analyze the relevant indicators， and the data was fitted to the comprehensive indicators by time series to obtain the trend of the comprehensive indicators of earthquake precursors.

Keywords： earthquake precursors;related index analysis;principal component analysis

2014年2月，新疆于田發生7.3级地震;2013年7月，甘肃省定西市岷县、漳县交界处发生6.6级地震，共造成95人死亡;2013年4月，四川省雅安市芦山县发生7.0级地震，共计造成196人死亡，1万余人受伤;2011年3月，云南盈江发生5.8级地震，造成25人遇难，314人受伤，10余万间房屋顷刻间倒塌损坏;2010年4月，青海省玉树藏族自治州玉树县发生7.1级地震，造成2 698人遇难、270人失踪;2008年5月，四川汶川、北川发生8.0级地震，造成69 227人遇难，374 643人受伤，17 923人失踪，此次地震是新中国成立以来国内破坏性强、波及范围广、总伤亡人数多的地震之一。

地震一次又一次地向人们袭来，尤其是2008年的汶川8.0级大地震，造成的破坏极大，全国人民陷入悲恸之中，令人深思。地震是地壳快速释放能量过程中造成的振动。虽然预测地震是世界性难题，但迄今科学界普遍认为，有可能反映地震前兆特征的指标不少于10个[4-7]。地震对人民和经济的伤害是巨大的，尽可能地了解、预测地震，尽量做到早预防、早撤离，显得如此重要。

当前，人们需要广泛查阅与地震相关指标的数据和分析方法，分析震前各指标数据特征，建立数学模型以度量各指标对地震发生的敏感程度，构建由某些或全部指标构成的综合指标，研究地震发生前的数量特征，使其尽可能地集中反映地震发生前的数据特征的统计规律。

1 预备工作

首先，根据地震的相关知识，查找与地震相关的12个指标，并搜集2005—2014年地震发生前15d的相关指标数据，分别用MATLAB画出该段时间每次地震各个指标的散点图。若是反映地震前兆的指标对地震敏感程度大，其在一段时间序列往往有比较大的变化幅度，因此观察这些散点图，得出最大的振幅，记为[Aij]（第[i]次地震的第[j]个指标的振幅，[i=1，2，...，7]表示2005—2014年发生的地震序号，[j=1，2，...，12]表示12个地震前兆指标），将7次地震各指标振幅与其所对应的震级做成一个矩阵，调用MATLAB软件中的CORRCOEF函数，求出各指标对地震的敏感程度。

其次，需要构建某些或全部指标构成的综合指标，使其尽可能得集中反映地震发生前的数据特征统计规律。人们可以应用主成分分析法，在力保原始数据信息不丢失的情况下，对高维变量空间进行降维处理，经过线性变换和部分信息舍弃，以少数的综合变量取代原有的多维变量[3]。

2 问题解决的过程及结果

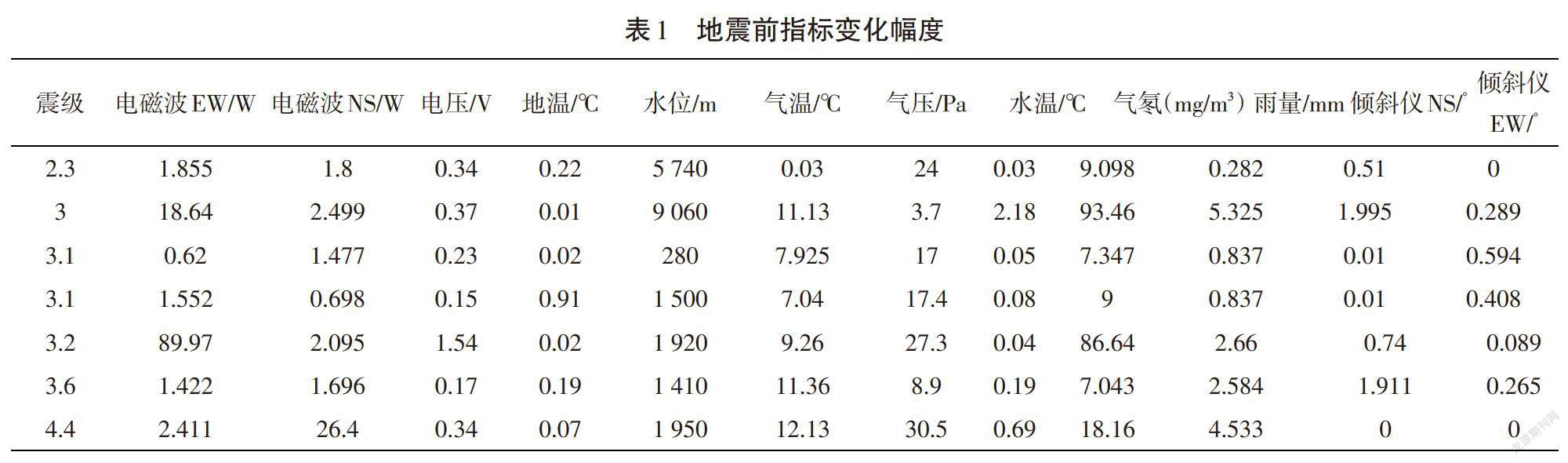
根据中国地震统计结果，笔者搜取到某地2005年1月1日至2014年6月30日按小时观测的12个指标数据，对所划时间段内的各指标散点图进行观察，得出地震前各指标的变化幅度，如表1所示。

针对表1数据，构建矩阵，用MATLAB软件中的CORRCOEF函数求出各指标与地震级别的相关系数。经比较，各指标对地震的敏感程度由大到小依次为：气温、电磁波幅度NS、雨量、水位、气压、地温、倾斜仪EW、水温、倾斜仪NS、气氡、电磁波EW、电压。因此，人们可以利用对地震敏感度大的气温、电磁波振幅NS、雨量等依次来判断地震发生的可能性。

下面用主成分分析法对各指标进行综合指标分析。一是对7月26日到8月6日的原始数据进行标准化处理。首先，对样本数据求平均，即

[Xi=j=1960Xij （i=1，2，...，7）]                      （1）

然后，对样本数据求标准差，即

[δi=j=1960（Xij-Xi）2 （i=1，2，...，7）]                    （2）

接着，对原始数据进行标准化处理，即

[Xij=Xij-Xjδi （i=1，2，...，12;j=1，2，...，960）]         （3）

二是根据标准化数据表，计算相关系数矩阵[R=（rij）12×960]。相关系数矩阵公式为：

[rij=1960j=1960（Xji-Xi）（Xjj-Xj）δiδj]          （4）

三是计算[R]的特征值。根据特征方程[R-λiI=0]，计算特征根[λi]，并使其从大到小排列，即[λ1≥λ2≥...λ12]，同时可得对应的特征向量[ui]，它们标准正交。[u1，u2，...，u12]称为主轴，得出特征值：[λ1]=4.349 45，[λ2]=4.340 93，[λ3]=3.309 17，[λ4]=0.000 395 387，[λ5]=1.915 58E-005，[λ6]=1.143 572E-005，[λ7]=1.147 11E-005，[λ8]=4.636 97E-006，[λ9]=2.731 133E-006，[λ10]= 8.919 1E-007，[λ11]=3.769 26E-007，[λ12]=1.996 629E-007。

四是计算贡献率。根据[ei=λii=112λi]，得出[e1]=0.362 5，[e2=0.3617] ，[e3]=0.275 8，[e4=e5=e6=e7=e8=e9=e10=e11=e12]=0.000 0。因此，[e1+e2+e3=1]。将[ei]进行降序排序：[e1>e2>e3>e4>e5>e6>e7>e8>e9>e10>e11>e12]。累计贡献率为：

[Em=i=1mλii=1pλi]                            （5）

其中，[Em≥85%]。下面计算主成分，即

[Zi=j=1960uijXj （i=1，2，3）]                     （6）

综合指标表达式为：

[Wj=i3eiZi （j=1，2，...，960）]                      （7）

通過对时间序列[Wj]在Excel中进行数据拟合，本研究得出了地震前兆综合指标的变化趋势，如图1所示。

由图1可以看出，地震发生前期，综合指标整体呈现上升趋势，可以作为预测地震发生的参考点。

3 结语

考虑到数据的波动性，通过对震级和幅度建立模型，笔者观察了震前15d的波形图，寻找突发性变化幅度最大的波作为对象，更好地反映临震前指标会出现突发性现象。建立的模型也能更好地反映各指标对地震的敏感程度。不足的是，人工取幅度会造成误差。人们要有效运用主成分分析法，合理构造各个指标的综合指标，如果有震级更强的地震数据，将会有更好的效果。

参考文献：

[1]郑阿奇.MATLAB实用教程[M].北京：电子工业出版社，2007.

[2]付强.数据处理方法及其农业应用[M].北京：科学出版社，2006.

[3]姜启源，谢金星，叶俊，等.数学模型[M].北京：高等教育出版社，2003.

[4]王喜珍，腾云田，高孟谭.基于树形结构的地震数据库系统设计方法[J].华北地震科学，2005（5）：11-13.

[5]王书明，朱培民，李宏伟，等.地球物理学中的高阶统计量方法[M].北京：科学出版社，2006.

[6]周克昌，李志雄，王松.地震前兆数据监视与管理系统[J].地震，2006（1）：115-122.

[7]梁平著.汶川故事[M].成都：四川文艺出版社，2011.