组合后验方差法在基准点稳定性分析中的应用

陈朔　王铁生　王世洋

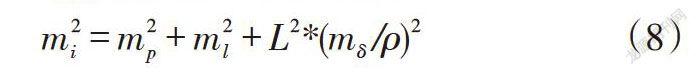
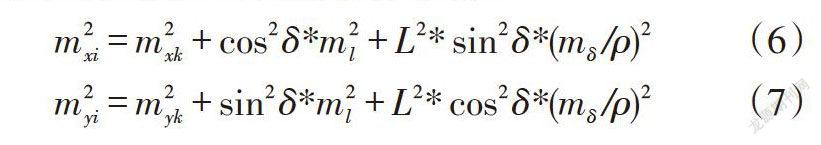
摘 要：工作基点的坐标是由各基准点的已知坐标延测过来的，假设基准点发生了明显变动，但仍将基准点视为已知点，则工作基点和变形监测点的坐标都必将受到干扰。本文以开封市民之家工程为研究对象，探讨建筑变形监测中基准点稳定的重要性。

关键词：变形监测;数据处理;组合后验方差法;稳定性

中图分类号：P207 文献标识码：A 文章编号：1003-5168（2019）23-0108-04

Application of Combined Post-verification Method in Stability

Analysis of Reference Point

CHEN Shuo WANG Tiesheng WANG Shiyang

（North China University of Water Resources and Electric Power，Zhengzhou Henan 450046）

Abstract： The coordinates of the working base point are extended from the known coordinates of each reference point. Assuming that the reference point has changed significantly， but the reference point is still regarded as the known point， the coordinates of the working base point and the deformation monitoring point will be disturbed. This paper took Kaifeng Citizen's Home Project as the research object， and discussed the importance of reference point stability in building deformation monitoring.

Keywords： deformation monitoring;data processing;the method of post-combination test;the stability

1 組合后验方差法和平均间隙法的内容和原理分析

1.1 组合后验方差法

1.1.1 内容。组合后验方差检验法用来判断基准点是否发生变动，剔除变动的基准点，再以稳定的基准点为已知点，对控制网进行平差。其本质是对所选基准点进行各种组合，用后验单位权方差构成统计量进一步验证，若基准点未通过原假设，则进行迭代运算，缩小动点范围，直到检验出动点并剔除该基准点。只有采用稳定的基准点进行监测，才能准确反映被监测物的变形情况，并提高监测精度[1-5]。

1.1.2 原理。①组合后验方差法实际是应用了统计学中假设检验[X2]（卡方检验），[X2]检验的原假设（基准点未发生变动），记作[H0]，其互斥对立假设即为备选假设（基准点发生显著变动），记作[H1]。对假设方向的选择，研究者立场与角度不同，会给出不同的假设，从而产生截然不同的结论。因此，对于一个假设检验问题，在建立假设时，需要分清自己的立场。

②该方法需要对基准点进行各种组合。例如，假如有[n]个基准点，分别取[n]个，[n-1]个，[n-2]个直到[n-i]个基准点进行组合，组合公式为：[Cmn=n！m！（n-m）！]。

③[X2]检验的原假设与备选假设如下。[H0]：E（[δ2∧]）=[δ20]，[H1]：E（[δ2∧]）>[δ20]。

构造统计量为：

[T=fδ2∧δ20～X2af]                          （1）

式中，[δ2∧]为后验单位权方差;[δ20]为先验单位权方差;[X2af]为分位值;[f]为自由度;[a]为显著水平，用来控制若[H0]为真经检验拒绝[H0]概率及犯“弃真”错误的概率，一般为0.05。当[T≥X2af]时，该组合存在变动的基准点。

1.2 平均间隙法的内容及原理

其主要思想是，先进行两期整体检验，若检验通过，则确认整体基准点是稳定的，否则就要找出不稳定的点。对两期观测成果进行稳定性检验，两期分别为第1、2周期[6-11]，其每期平差成果的单位权方差估值为：

[σ21=VTPV1f1]                        （2）

[σ22=VTPV2f2]                         （3）

通常，两期观测是等精度观测，可以串起来求一个共同的单位权方差验后估值，即

[σ0=VTPV1f+VTPV2f]           （4）

式中，[f]为两期观测的自由度之和，[f=f1+f2]，所以可用[σ2d]及[σ20]两个方差估值的比来检验[d]中是否位移信息显著。原假设[H0：σ2d=σ20]，备选假设[H1：σ2d>σ20]。在[H0]成立下，统计量为：

[F=σ2dσ20→Ffd，f]                 （5）

如果[F>Fafd，f]，则拒绝原假设[H0]，认为存在动点，否则认为位移不显著。

2 两种常用方法比较

平均间隙法是一种整体检验法，经检验，若认为位移量显著是指平均点位，不是所有点位移量都显著，要想锁定哪些点是稳定点，哪些点是动点，还需要用到单点检验法，用[t]分布做检验试验。组合后验方差法比较简便有效，只需进行小范围组合，进行迭代运算缩小动点范围，也要构成统计量进一步用[X]检验，锁定变动点。

3 工程实例——开封市民之家基准点稳定性检验

3.1 工程概况

开封市民之家工程于2014年投入使用，每年需要定期进行变形监测，以确保工程框架结构稳定，工程周围设立有很多基准点，但有些基准点受所处地质和外界干扰产生变动，需要进行基准点的稳定性检验，以确保后续变形监测方案精准施测。

3.2 工程基准点及监测点概况

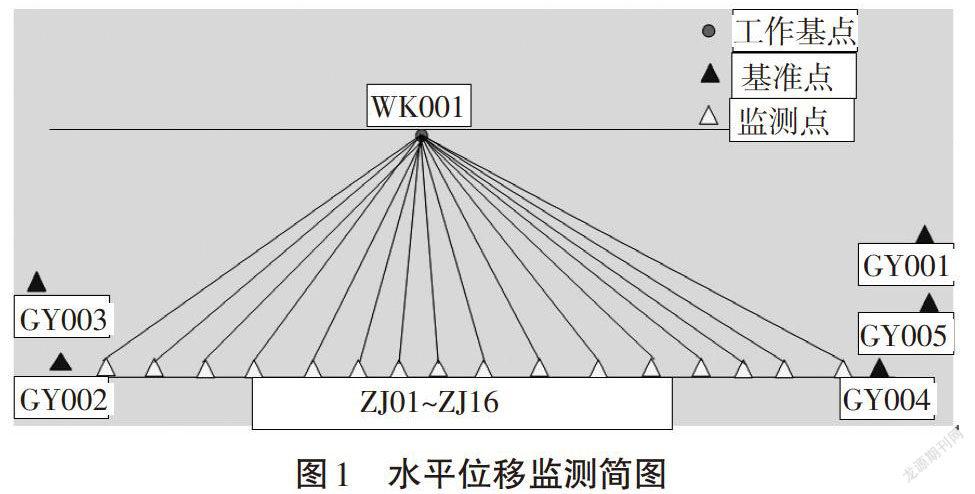
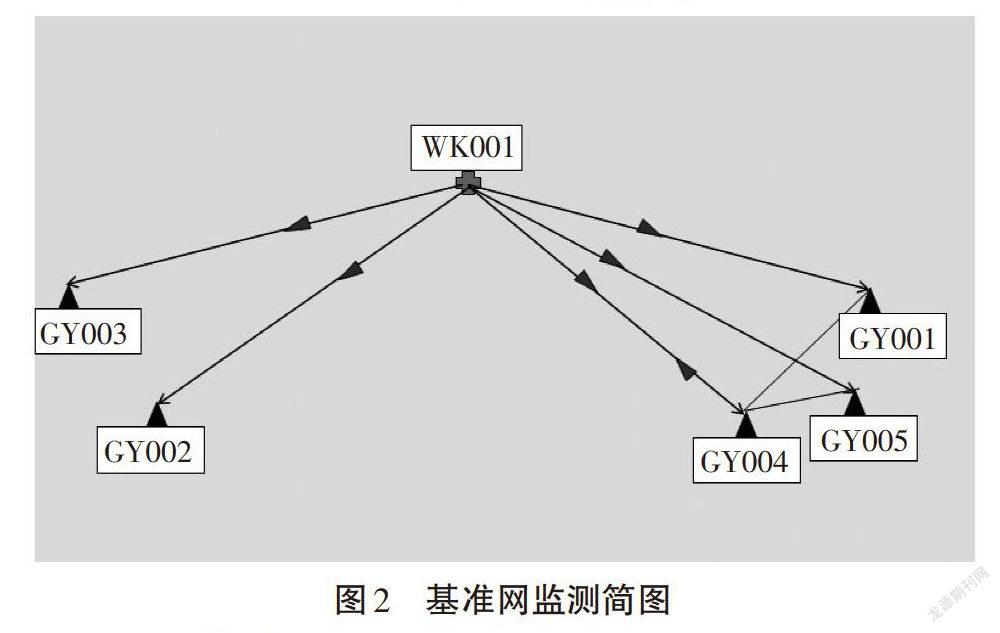
水平位移监测示意图如图1所示。部分基准点GY001、GY002、GY003、GY004和GY005位于施工现场外稳定区域，点位上都设置强制对中观测墩。为方便实验，变形监测点位为ZJ1～ZJ16，共布设16个。仪器架设在工作基点WK001上，分别对GY001、GY002、GY003、GY004和GY005观测6个测回。变动仪器设站位置，将仪器架设在基准点GY004上，分别对WK001、GY005和GY001进行6个测回。检核仪器采用莱卡TCA2003进行边角观测（测角精度[0.5″]，测距精度1mm+1ppm），稳定性有明显改善。基准网监测简图如图2所示。

3.3 数据分析

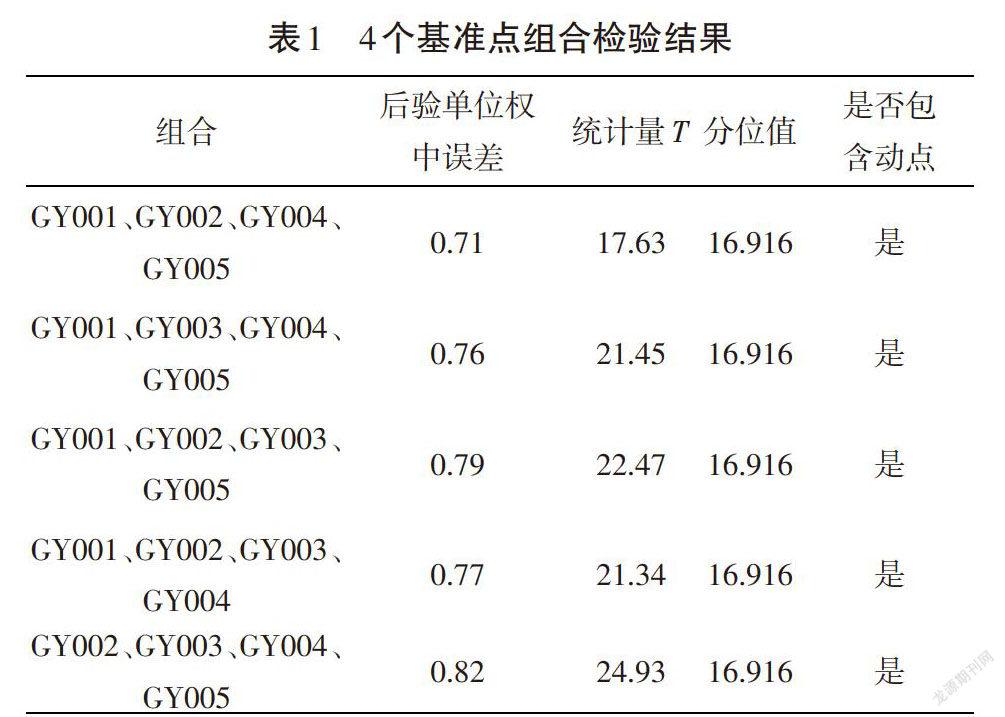
GY001、GY002、GY003、GY004和GY005为已知点，WK001为待定点，定权时先验单位权中误差（特根据各项误差来源及以往使用经验事先对误差的估计）取0.5，平差后解得工作基点WK001的坐标（547.256 3m，834.786 5m），后验单位权中误差（特指工作完成后，采用更高精度的仪器方法来评定已完成工作的精度）为0.79（由[VTPVr]可得），后验单位权中误差显著大于先验单位权中误差。由相关参考文献得出排除观测值粗差的情况下大致确定已知基准点发生变动，而后进行检验，得统计量[T]=11×0.793/0.501=27.46。一般認为[a]=0.05，分位置可通过查表确定，[X20.05（11）]=19.675，[T>X2a]，表明5个基准点中存在显著变动的基准点。继续选取不同基准点组合，对变动基准点进行检验（设计组合数为[m]）。[m]=4时，可进行5种组合，根据相关公式进行检验，检验结果如表1所示。

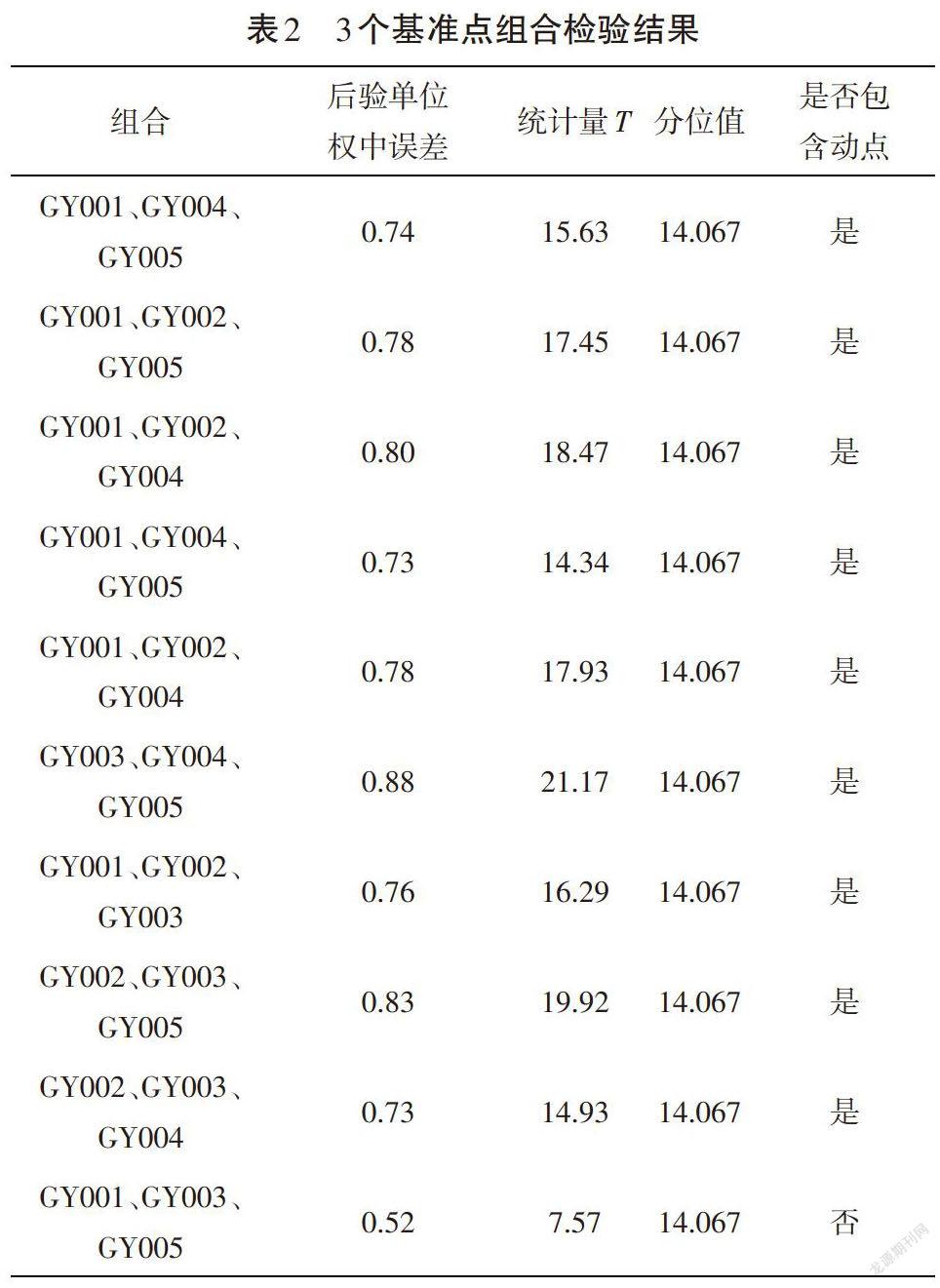
由表1可知，所有组合都含有有变动点，可以确定基准点中至少有2个不稳定点。当[m]取3时，可进行10种组合方式，验后结果如表2所示。

由表2可知，组合GY001、GY003、GY005通过了检验。由此可判断变动基准点为GY002和GY004。将GY001、GY003、GY005作为已知点进行平差。后验单位权中误差为0.46，WK001（547.256 8m，834.785 5m）点位中误差为0.50mm。同时，可得到GY002和GY004点位坐标分别为（413.675 3m，879.554 3m）、（893.146 3m，901.276 8m）。GY002在[X]方向变动1.2mm，在[Y]方向变动1.0mm;GY004在[X]方向变动1.2mm，在[Y]方向上变动1.7mm。

3.4 监测点精度分析

基准点稳定性检验后，可获得稳定的基准点和工作基点，通过极坐标法可获得监测点坐标。监测点[（X，Y）]方向中误差可根据误差传播定律获得：

[m2xi=m2xk+cos2δ*m2l+L2*sin2δ*（mδ/ρ）2]         （6）

[m2yi=m2yk+sin2δ*m2l+L2*cos2δ*（mδ/ρ）2]         （7）

式中，[mxi]与[myi]为第[i]个监测点在[X，Y]方向上的中误差;[mxk]为工作基点WK001在[Y]方向上的中误差;[δ]为测站到第[i]个监测点方向与已知方向的夹角;[L]为测站到第[i]个监测点之间的距离;[ml]为仪器测距中误差;[mδ]为仪器测角中误差。监测点点位中误差为：

[m2i=m2p+m2l+L2*（mδ/ρ）2]                    （8）

式中，[mp]为GY001的点位中误差。

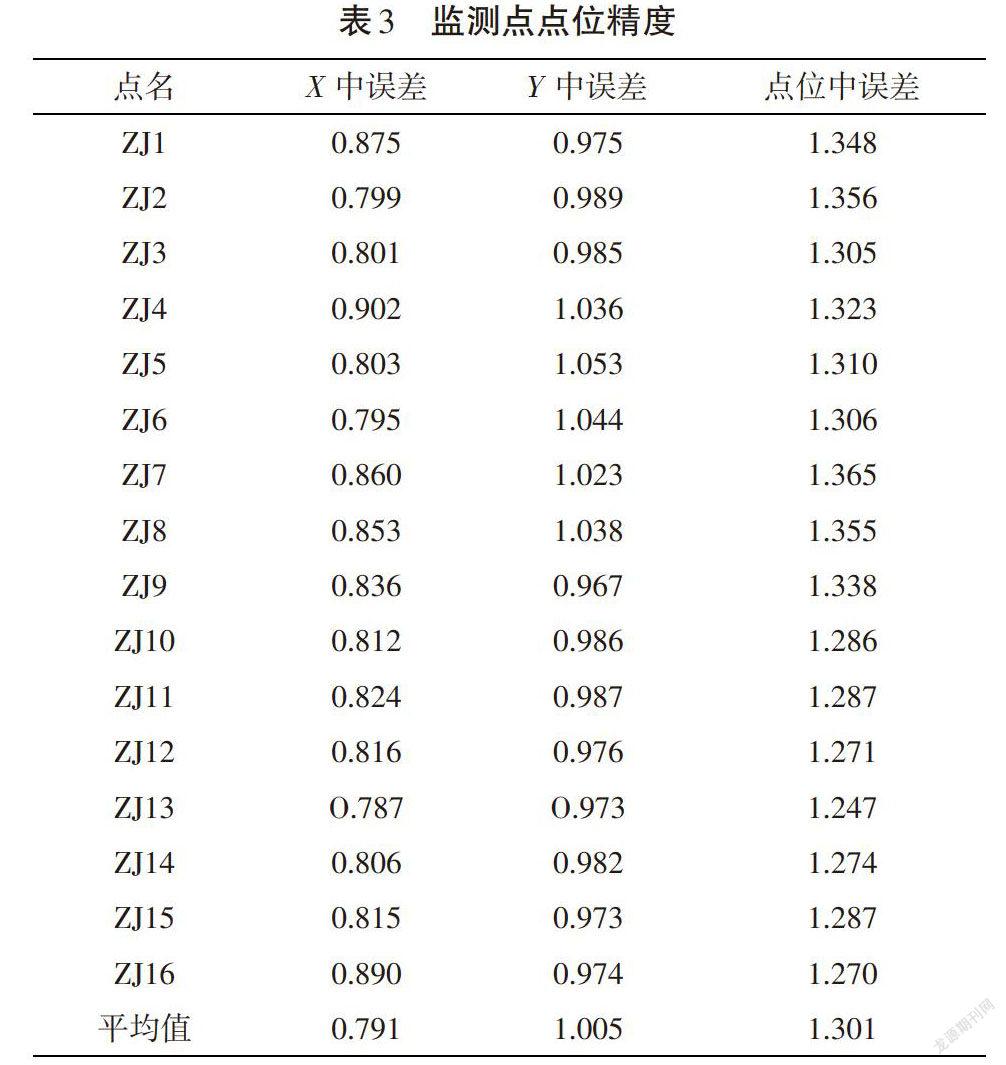
以GYOO1、GY002、GY003、GY004、GY005为基准点，监测点点位精度如表3所示。

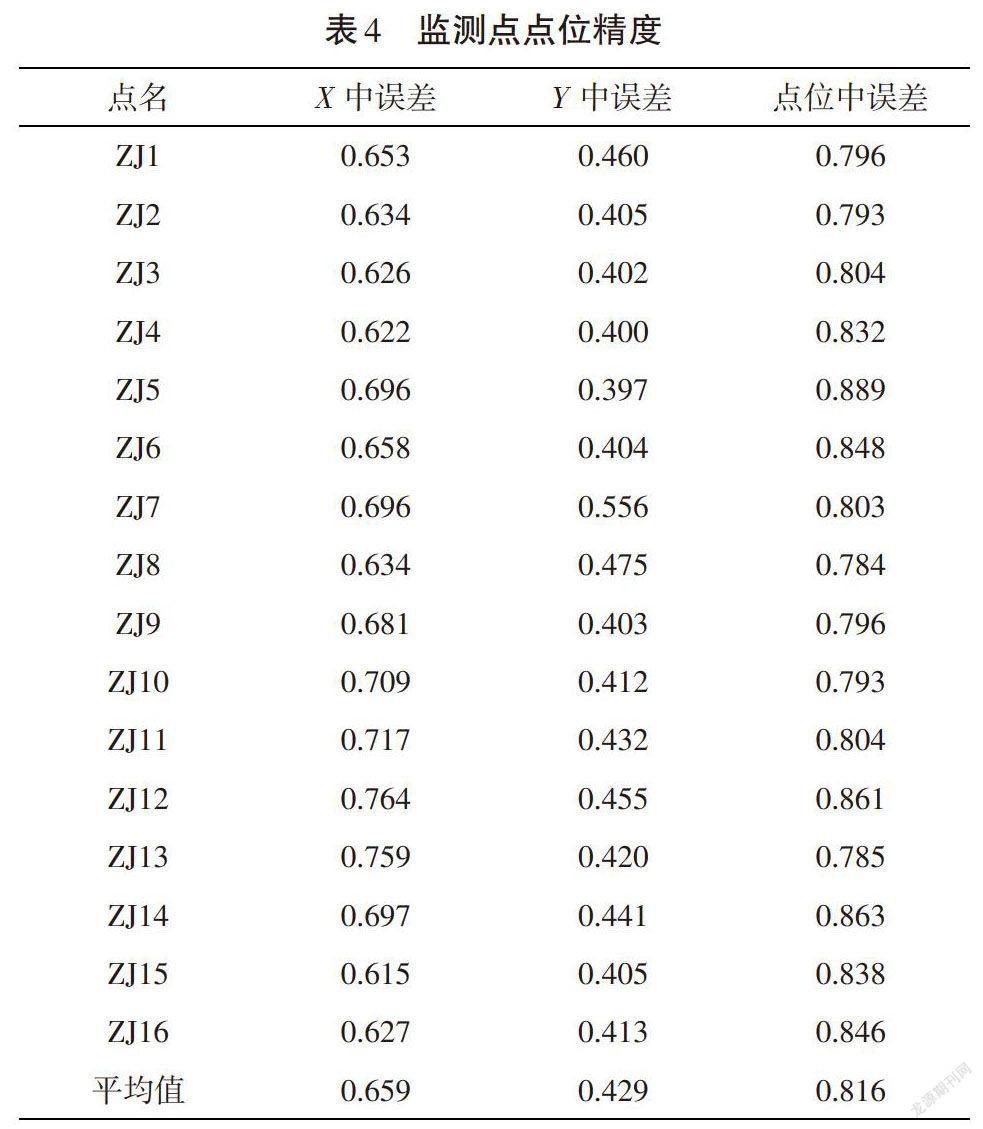
从表3和表4可以看出：以组合GY001、GY002、GY003、GY004、GY005为基准进行平差计算，监测点[X]方向中误差在0.787～0.902mm，平均值为0.791mm;[Y]方向中误差在0.968～1.058mm，平均值为1.005;点位中误差在1.270～1.365mm，平均值为1.301mm。以组合GYOO1、GY003、GY005为基准进行平差计算，监测点X方向中误差在0.618～0.772mm，平均值为0.659mm;[Y]方向中误差在0.328～0.516mm，平均值为0.429mm;点位中误差在0.689～0.998mm，平均值为0.816mm。对变动基准点GY002和GY004进行剔除，监测点方向精度和点位精度明显提高，能达到该工程水平位移监测精度要求。

4 结论

组合后验方差法在基准点稳定性检验的应用的确是一种较为简便有效的方法，与传统的平均间隙法、分块间隙法等比较具有明显优势。通过开封市民之家实例分析，本文验证了该方法的可行性与简便性。

将组合后验方差法运用到水平位移监测过程中发现：保证基准点稳定性的重要性不言而喻，剔除变动点前后所获得的监测点坐标差别很大。该检验法经迭代运算锁定出变动点，明显提高监测点位精度，对工程监测准确性影响较大。

参考文献：

[1]伊晓东，李保平.变形监测技术及应用[M].郑州：黄河水利出版社，2007.

[2]张正禄.工程测量学[M].武汉：武汉大学出版社，2005.

[3]黄声享，伊晖，蒋征.变形监测数据处理[M].武汉：武汉大学出版社，2003.

[4]余学祥，徐绍铨，吕伟才.变形监测数据处理自动化[M].徐州：中国矿业大学出版社，2004.

[5]张过之.衡阳隆中高层沉降观测报告[R].洛阳：衡阳建筑规划设计院，2012.

[6]邱卫宁，黄加纳.误差理论与测量平差基础[M].武汉：武汉大学出版社，2003.

[7]张书毕.测量平差[M].徐州：中国矿业大学出版社，2008.

[8]丁宁.高层建筑物变形监测数据处理与分析[D].济南：山东建筑大学，2006.

[9]武兴岩，全广军，安永建.高层建筑的沉降变形监测及数据处理分析[J].科技信息，2011（1）：344-345.

[10]冯待飞，杨伟，陈少川.高层建筑中的沉降监测与数据处理[J].华北国土资源，2009（3）：53-54.

[11]欧阳德诚.一元线性回归方程在建筑物沉降预测中的应用与探讨[J].工程勘察，2010（6）：66-70.