基于AHP-TOPSIS法的供应商选择研究
武庆伟
(北京物资学院,北京101149)
1 引言
随着贸易摩擦的不断加深,许多行业都受到了贸易摩擦的影响,并且面临着产业升级转型的压力,各企业所处的供应链的位置以及与供应商之间的关系显得十分重要。企业间的市场竞争也越来越激烈,供应链上的上、下游企业所面临的生存压力越来越大。因此,选择优质的供应商就变得非常重要。近几年,由供应链管理思想所倡导的快速反应性市场需求、战略管理和高度柔性等目标,成为企业追求的趋势[1]。
2 供应商评价指标体系的构建
通过研究、归纳、整理供应商选择与评价指标体系的国内外文献的研究,发现国内学者对供应商选择与评价的理论和实践应用做了很多的研究。其中主要有两个方面[2]:一方面是对评价与选择的方法和模型进行了研究;另一方面是对所选用的评价指标体系以及指标的相对重要性、指标体系及其相对重要性在不同时期变迁的研究,多侧重于研究怎样对指标值进行合理地处理和如何恰当地对定性问题进行定量化处理。供应商选择与评价是一个多属性决策问题,目前尚未形成成熟的评价指标体系,通过阅读大量相关文献,本文主要考虑从质量能力、供货能力、价格水平、服务水平、开发能力5 个方面构建评价指标体系。
3 AHP-TOPSIS 模型
层次分析法(Analytic Hierarechy Process,AHP)是1973年美国匹兹堡大学著名的运筹学家萨蒂(ThomasL.saaty)提出的定性与定量相结合的评价决策分析法,它是一种处理多目标、多决策、问题相对复杂、定量与定性相结合的方法。层次分析法的提出无论在理论研究上还是在实际工作中都得到了极为广泛的应用与发展。TOPSIS 法的基本原理是通过检测评价多个对象,并把最优解与最劣解的距离进行排序,若评价对象离最优解与最劣解都最近,则此种情况为最好结果,否则不能认为是最优[3]。其中,最优值是评价指标的最优解。最劣值是评价指标的最差解。
AHP-TOPSIS 法可以归结为以下几个步骤。
3.1 建立决策矩阵
在多目标决策问题中,假设有A1,A2,…,Am共m 个方案组成方案集A={A1,A2,…,Am},每个方案的评判指标a1,a2,…,an组成指标集a={a1,a2,…,an},每个评价目标的评价指标均有一个指标值。用各个指标值建立决策矩阵。
3.2 构造标准化矩阵
对原始数据进行归一化处理和标准化处理,并得出规范的决策矩阵,见下式:
Yij=(yij)m×n
其中,yij=
3.3 构造加权决策矩阵
得到加权后的决策矩阵Z=(Zij)m×n。其中Z=wj·yij,(i,j∈Z+),式中Wj由层次分析法得到的权重系数确定。
4 实例应用
4.1 指标体系构建
目前,某公司需要在现有供应商中进行合作伙伴的选择。现在有3 家较为适合的供应商,根据上文设定的指标体系构建了层次递阶结构如图1所示。
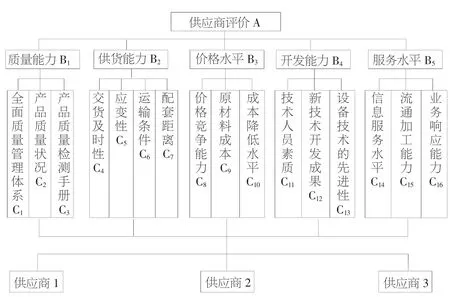
图1 供应商评价指标结构图
4.2 评分结果
根据该公司对3 家供应商的调查,通过专家打分的形式得到具体的评分如表1所示。
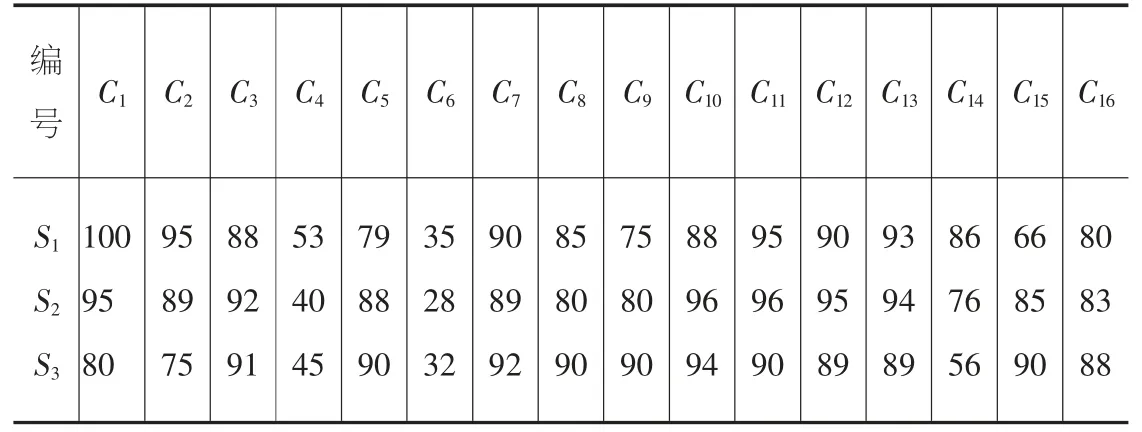
表1 各供应商评价指标值
4.3 一级二级指标一致性检验
根据设定的5 种一级指标和16 种二级指标通过两两进行比较判断后,得到判断矩阵如表2所示。
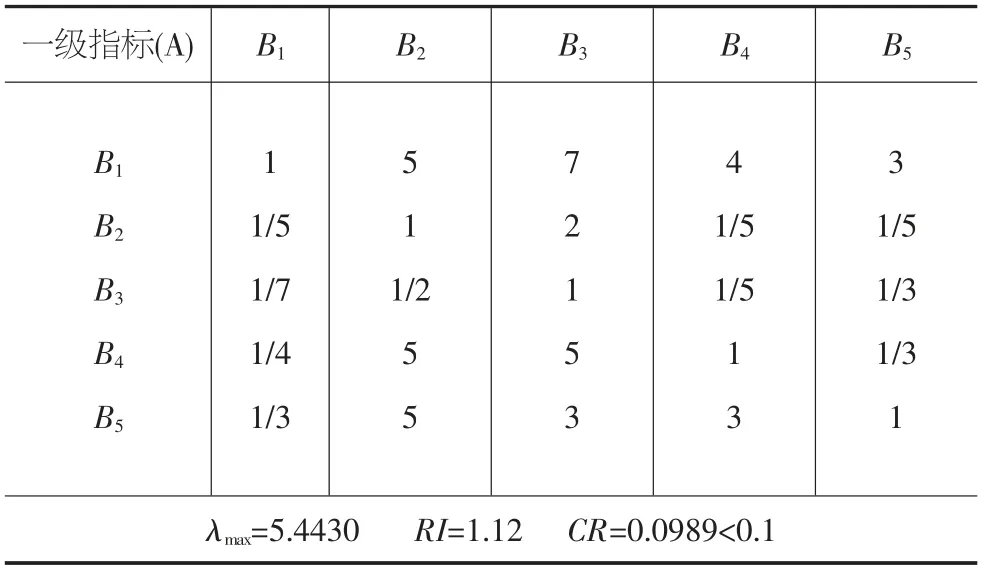
表2 一级二级指标判断矩阵
通过判断矩阵分别得出权重,具体权重如下:
W0=(0.4778,0.0624,0.0491,0.1653,0.2454);
W1=(0.5278,0.3325,0.1397);
W2=(0.0704,0.5512,0.2531,0.1253);
W3=(0.2109,0.0842,0.7049);
W4=(0.6333,0.2605,0.1062);
W5=(0.2828,0.0738,0.6434);
根据各判断矩阵的权重得综合权重为:
W=(0.182,0.1425,0.0655,0.0324,0.2523,0.0329,0.0873,0.1296,0.08540.0538,0.0109,0.0026,0.0638,0.0053,0.0043,0.0364)
4.4 计算加权规范决策矩阵

5 结语
从文章可以看出,改进后的供应商选择与评价方案对于
企业的实际选择具有很高的可行性。同时,在选择过程中层次分析法(AHP)和TOPSIS 两个方法的使用是科学的、合理的和恰当的,对于以后解决供应链管理中的多目标、较复杂的决策性问题有很好的实际意义。使用该方案后,企业在供应商选择中更加规范科学,起到降本增效的作用,这也有利于企业更好的发展。

