大时间步长下体积守恒的实时水体模拟

朱奎鑫，盖 孟，赖舜男

大时间步长下体积守恒的实时水体模拟

朱奎鑫1，盖 孟2,3，赖舜男2

(1. 北京大学深圳研究生院，广东 深圳 518055；2.北京大学信息科学技术学院，北京 100871；3. 北京大学北京市虚拟仿真与可视化工程中心，北京 100871)

基于物理的流体仿真可以真实地捕捉水的运动，一种常用的实时模拟方法是基于二维浅水方程进行水体仿真。首先介绍了二维浅水方程，并提出一种新的求解方法，通过一种体积守恒的隐式半拉格朗日方法进行计算，在保持稳定的同时允许较大的时间步长，然后额外增加修正步以保证计算过程中体积守恒。此外提出了一种基于动量守恒的流固耦合方法，可以实时地模拟出较为真实的水体，并且保证了水体体积始终守恒，效果良好。

浅水方程；半拉格朗日；体积守恒；大时间步长；流固耦合

流体运动是一个复杂的现象，很难实时在计算机上进行有效模拟，折中的方法是通过模拟水面来近似模拟水体，只需要使用二维区域上的高度场即可进行实时模拟。常用的方法有2种，一种是基于谱的模拟[1]，此方法非常稳定且细节丰富，但缺点是难以与移动的障碍物相互作用；另一种是使用基于物理的浅水方程进行模拟。本研究以二维浅水方程组为基础，提出了一种高效、稳定、体积守恒的流体仿真算法。通过半拉格朗日方法的使用，实现了较大的时间步长下的稳定模拟，这种基于物理的流体模型能够产生真实的波运动，对流体做到实时合理的仿真。

本文首先对浅水方程进行了描述，以此为基础建立了流体仿真模型。浅水方程是由纳维-斯托克斯方程推导而来，虽然无法模拟三维流体或带有黏度的流体，但是由于在高度项上进行了简化，计算量大大降低，使得求解效率提高，可以实现对流体的实时模拟。

然后，详述了一种质量守恒的半拉格朗日方法。人们知道，常规的半拉格朗日方法无法做到质量守恒，无法满足物理仿真与实际相符，通过在常规方法之后进行的扩散操作的改进，保证了平流前后质量守恒，对于流体仿真具有重大意义。

之后，对基于二维浅水方程的流体仿真进行实现。在该模型中，采用改进的隐式半拉格朗日积分法求解，再使用修正步弥补求解时的体积损耗，在保证稳定性的同时，允许较大的时间步长。

在此模型上实现了流固耦合的技术，借助有向距离场来判断交互区域，然后基于动量守恒进行单向交互，取得了很好的效果。

最后，通过演示该模型展示流体模拟的效果，并与其他模型进行了比较，证明了本文方法体积守恒、算法稳定、计算效率高。

1 浅水方程

浅水方程是描述浅水流动的数学模型，常用于实时流体运动的仿真计算。在流体动力学中，通常水平长度比垂直长度大得多，在此条件下，可以得到沿水深方向的静水压力分布，并根据纳维-斯托克斯方程导出浅水方程。有时也会引入水深方向的平均化，导出浅水方程的另一种形式。本文使用的浅水方程式为

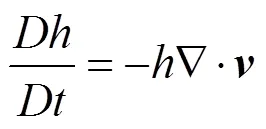
其中，为水平面高度；为水的深度，即水平面高度减去地形高度；为速度；为重力加速度；为时间。

浅水方程没有黏性项，水的深度方向速度可忽略，所以模拟时仅限于二维无黏流体，对于高黏度流体，飞溅或破裂的流体无法模拟。然而，其可充分地模拟一大类流体的运动，且计算效率极高，是进行实时流体模拟的最好选择。

求解浅水方程有多种方法，中外研究者大都采用有限体积法以保证体积守恒[2-3]，不过该方法在较大时间步长下表现不稳定；有些隐式差分方法，可以保证无条件稳定[4]，却不能保证体积守恒，本文方法希望可以同时具有这2个优点。

2 半拉格朗日方法

半拉格朗日方法[5]可以看作是欧拉方法和拉格朗日方法的混合体。欧拉方法保持网格的规则性，但为了保持稳定，需要较小的时间步长。拉格朗日方案不受稳定性要求的限制，允许更大的时间步长。半拉格朗日方法试图将2种方案的优点，即欧拉方法的规则性和拉格朗日方法的稳定性结合起来，在每个时间点，进行网格点值计算时，沿着粒子轨迹进行求解。

以式(1)为例，等式左边展开为

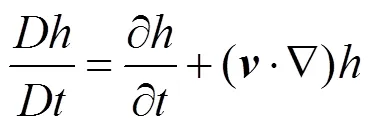
公式右边的第1项称为局部项，第2项为平流项。其实，半拉格朗日法就是用拉格朗日的思想求解平流项，然后在固定的网格上求解局部项。

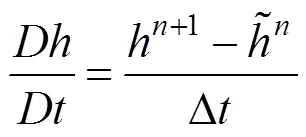
类似的，有

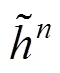
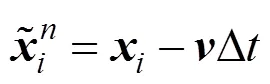
其中，为当前时刻网格的速度。

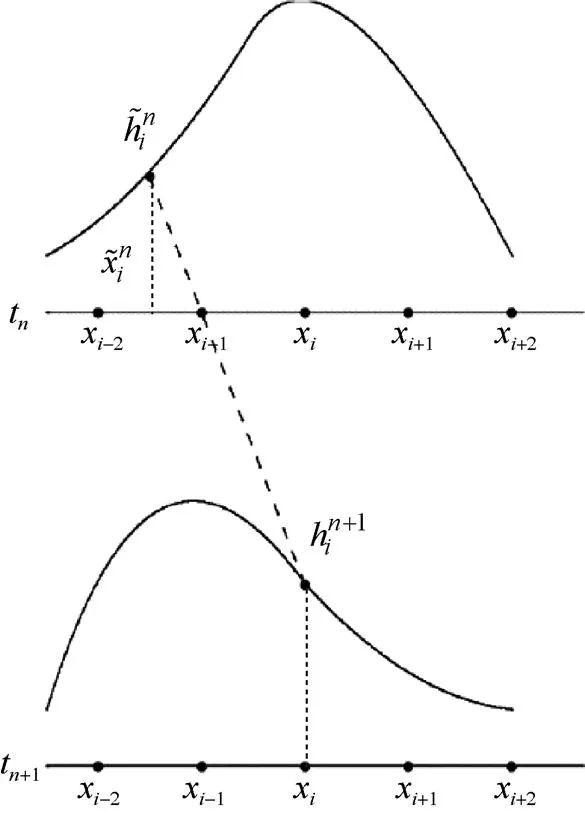
图1 半拉格朗日方法

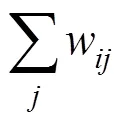
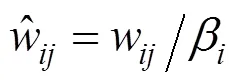
图2中的()和伪代码中的()代表的是α，为每个网格的流入量权重，而()代表的是网格存储的物理量。在循环过程中，α逐渐向1靠拢。

上述扩散权重的方法，也存在一个问题，即迭代次数过多，对实时仿真造成影响。一种加快该过程的方法是继承上一次的误差，在每帧权重扩散之前，加上上一帧最后计算的结果与1的差，然后再进行权重扩散。在实际工作中，这样可以减少迭代次数，提高仿真效率。

图2 扩散权重方法

3 方程求解

进行方程求解模拟流体运动的流程如下：

(1) 使用本文改进的半拉格朗日方法进行平流。

(2) 将方程离散化，隐式求解。

(3) 考虑求解中损失的体积，在修正时进行体积补偿。

3.1 半拉格朗日平流

半拉格朗日平流，使用本文改进的半拉格朗日方法，满足任意β和α均等于1的条件，这样既保证了体积守恒，也实现了较合理地仿真效果。使用了继承误差的方法后，在仿真过程中，迭代次数不超过10次即可收敛，可既达到目的，也满足了的实时仿真的要求。

3.2 隐式求解

在进行平流之后，部分研究者采用半隐式的方法[8]，本文采用文献[9]隐式求解的方法，1阶精度，但对于流体模拟已经足够，式(1)和式(2)可以写成如下形式

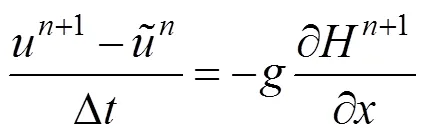
式(7)~(9)中，为速度方向的分量；为速度方向的分量。由于采用隐式求解，所以等号右边均使用了下一时刻的状态，式(7)等号右侧的h，本应为h+1，但这将变成非线性方程组求解问题，求解困难，因此本文使用h来近似h+1。

现在开始讨论网格如何离散化。在整个模拟过程中，必须在空间的各个点存储许多不同的量(速度、高度等)。很明显，需要采用一种合理的布局。最简单的方法是，将所有信息存储在同一个网格中心上，但这并不是最佳的方法。很早以前，MAC网格就被提出[10]，目前在流体模拟中被广泛使用。该网格也被称为交错网格，因其在不同的位置存储不同的物理量，如在网格中心存储高度，网格边上存储速度。在二维情况，MAC网格中的单元格结构如图3所示。

根据这个网格结构，可将高度、速度相关的公式进行空间离散化，形式如下

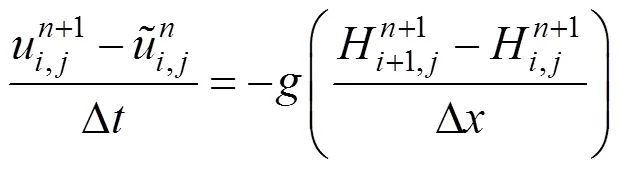
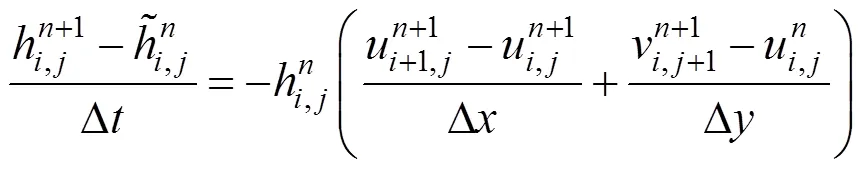
将速度公式带入到高度公式中即可得到一个线性方程组，使用雅克比迭代求解该大型稀疏线性方程组，时间步长较小时，迭代10次以内就可以得到满意的结果。

3.3 体积修正

在实现的流体模拟中，每一步都要保证体积守恒。平流时采用了改进的半拉格朗日方法，保证了平流前后体积守恒，但是在进行隐式求解时，无法保证体积守恒，为此，需要找到求解过程中的体积损失。

根据高度公式，不难发现，如果要保证最后体积守恒，线性方程组的所有方程等号右侧相加应该等于0，隐式求解时的方程组并未满足该条件，所以体积不守恒。现在要对体积进行修正，在更新高度时，等号右侧统一地加入一个相同形式的量，使得所有网格等号右侧相加等于0。

通过上述描述已可以实现在开阔区域的水面模拟，如图4所示。

图4 水面上的水波

3.4 边界处理

干湿边界处理在浅水方程中也很重要，有很多方法得到了广泛应用[11]，将边界进行标记，然后特殊处理。对于本文的模拟来说，在水流开始运动之前，有水的网格水平面应该高于附近没有水的网格地形。否则，两者之间的面就被标为障碍。对于在MAC网格中标记为障碍的面，速度在每个时间步结束时设置为0，而且在平流步中不更新。满足以下条件的面视为障碍，即

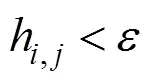
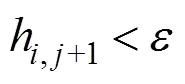
其中，为一个大于0的小常数，均定义为0.000 1。类似的情况也适用于交错网格的其他面。按照本文的处理方法，图4所示的水体碰到边界后如图5所示。

图5 水波碰到边界

3.5 流固耦合

流固耦合在水体模拟中是一个重要的话题，为了使刚体与水体之间能有效地相互作用，本文提出了一种模拟流固相互作用的单向耦合方法，即水体的运动只能受到刚体的影响，而不对刚体的运动产生影响。

流固耦合有2个关键技术，一是如何确定交互区域，二是确定交互区域之后的相互作用。

使用有向距离场来确定交互区域。有向距离场(signed distance field, SDF)，“有向”、“距离”、“场”这3个词非常精确的描述了SDF究竟是什么。SDF是到(多边形模型)物体表面最近距离的采样网格。距离的正负号表示在物体的外部或内部，距离值为正表示点在物体外部，反之在内部，若距离值为零表示点在物体表面。可将交互的固体模型文件转化为有向距离场。对于浅水方程的每个网格，可对高度进行离散，依次就此网格的当前高度判断距离值是否为负，并判断是否在交互物体内部。如果在交互物体内部，那么此网格的当前高度就是交互区域，这样，在二维的水面上得到了一个三维的交互区域。

确定交互区域之后，根据动量守恒进行交互。对于当前网格，如果处于交互区域，认为交互区域的速度等于固体的速度。然而，由于交互区域是三维的，可能某些高度处于交互区域，或不属于交互区域，但是对于当前网格，只有一个速度，即

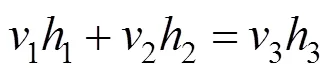
其中，1为固体速度；2为交互之前的水体速度；3为交互之后的水体速度；1为当前网格根据深度离散化后，处于交互区域的高度和；2为不处于交互区域的高度和；3为水深，1+2=3。

交互算法流程如下：

步骤1.对于交互的固体模型转化为有向距离场。

步骤2. 对于每个时间步长：

(1) 确定有向距离场在整个计算网格上的大致投影区域。

(2) 对于投影区域的每个网格：①将网格上的高度离散化，从上到下遍历每一个离散坐标，判断坐标点是否在物体内部；②对每个网格，按照动量守恒，更新当前网格速度。

(3) 继续进行浅水方程计算。

按照此方法，水面上划过的木块尾迹，如图6所示。

图6 水面上的划过的木块

4 结果和分析

4.1 实验结果

本文模型可以模拟许多的流体运动。为了满足实时要求，还借助了GUDA进行GPU并行加速。所有的流体模拟都是在CPU为inter(R) Core(TM) i5-4570 3.20 GHz，显卡为NVIDIAGeForce GTX970，操作系统为Windows10，使用CUDA9.1进行并行加速计算。

图7使用固定的边界，对带有障碍物的矩形水池中的水波进行了实时模拟。此实验中模拟的网格大小为256×256，每帧间隔为0.1 s。

图7 矩形水池中的水波

本文的模型是基于物理的，因此只需要为其提供一组初始条件，也就是模拟开始时水面的形状，水面就会根据浅水方程自然演变。图8是水从柱子间流出，较为真实地模拟了水体效果。

图8 柱子间的水流

由于本文采用隐式半拉格朗日解法，可以使用较大时间步长进行模拟，与较小时间步长相比，效果近似，但速度提升较快。图9是时间步长分别为0.1 s和1.0 s的2个实验结果对比。在时间步长较大的情况下，隐式求解迭代次数增多，在保证体积守恒的情况下，依然可以保持实时模拟。时间步长为0.1 s和1.0 s时，模拟100帧的时间，分别为26 s和17 s。

图9 不同时间步长 (左侧为0.1 s，右侧为1.0 s)

关于固体与水体之间的交互，从效果上看还是很好的，较好地模拟了固体对水体的作用力，如图10所示。

图10 水面上行驶的小船

4.2 比较与分析

显式方法由于其简单性，被用于流体模型的许多实现中。但其主要缺点是对时间步长有严格的限制，数值解可能与真实解呈指数发散。通过选择隐式积分方法，保证了稳定性不受梯度项大小的限制。通过采用半拉格朗日方法，还确保了时间步长不受CFL条件的限制。只要有足够的精度估计出发点，可确保算法是稳定的。比较该算法与采用半拉格朗日方法的算法的稳定性，以2010年CHENTANEZ和MÜLLER[12]的算法作为比较，其通过有限体积法同样实现了体积守恒。两者之间的效果对比如图11所示，初始场景是3个水柱，2种方法的效果基本相同。在本文的测试案例中，隐式半拉格朗日方法得到的最大时间步长比文献[12]方法大10倍以上，本文的CFL数在超过10时依然保持了模拟的稳定性。

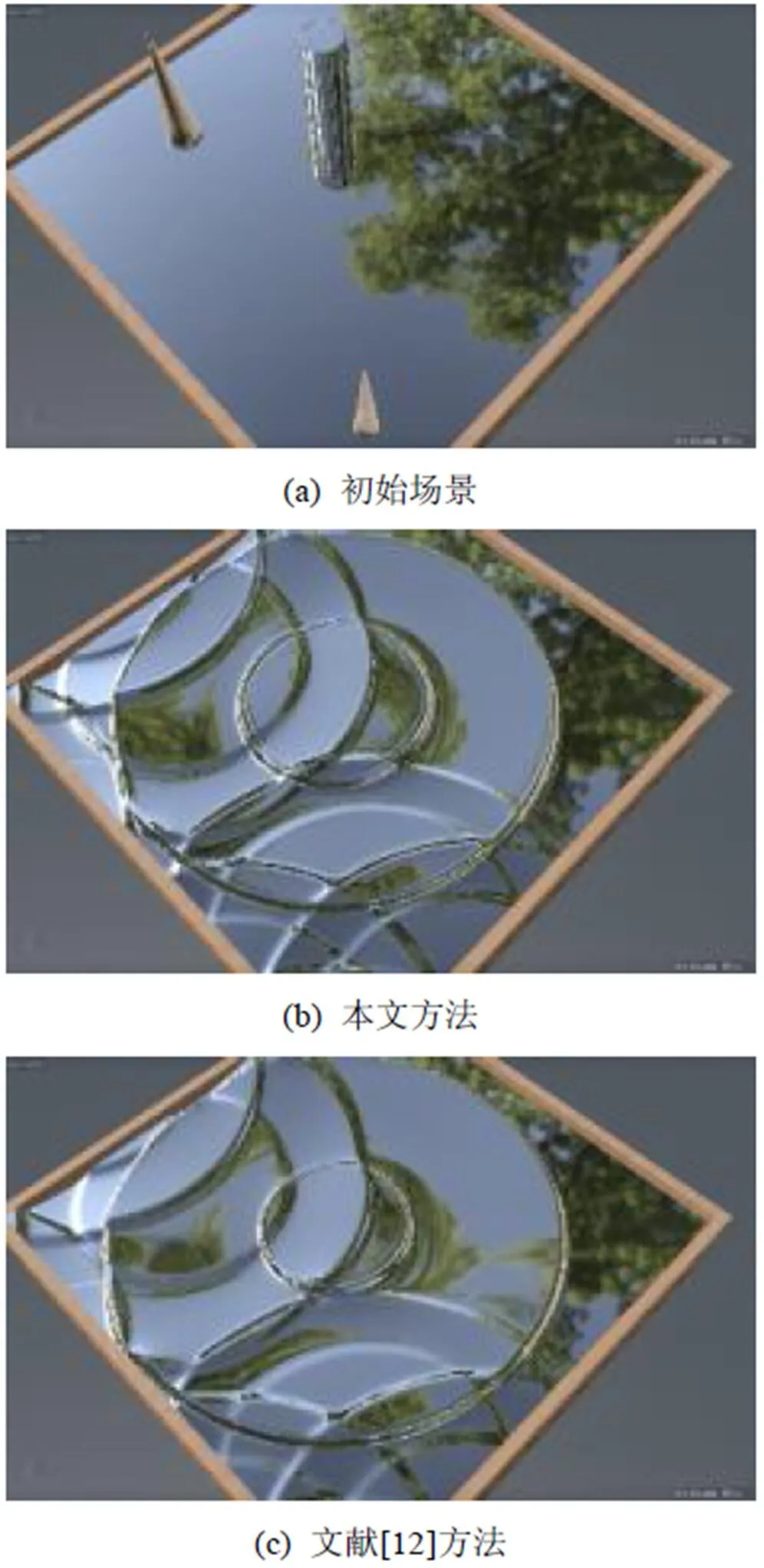
图11 本文方法与文献[12]方法的效果比较

进一步研究了本文算法的体积守恒特性。在不增加或去除水的情况下，通过对水深进行求和得出的总体积，在整个模拟过程中应该保持不变。在本文所有的实验中，水的体积变化小于0.01%，由于变化极小，可认为实现了体积守恒。与文献[9]的方法相比，如图12所示，使用2种方法模拟图7的场景，其效果基本相同。不过同样是半拉格朗日隐式求解，如图13所示，本文方法保证了体积守恒。

图12 本文方法与文献[9]方法的效果对比

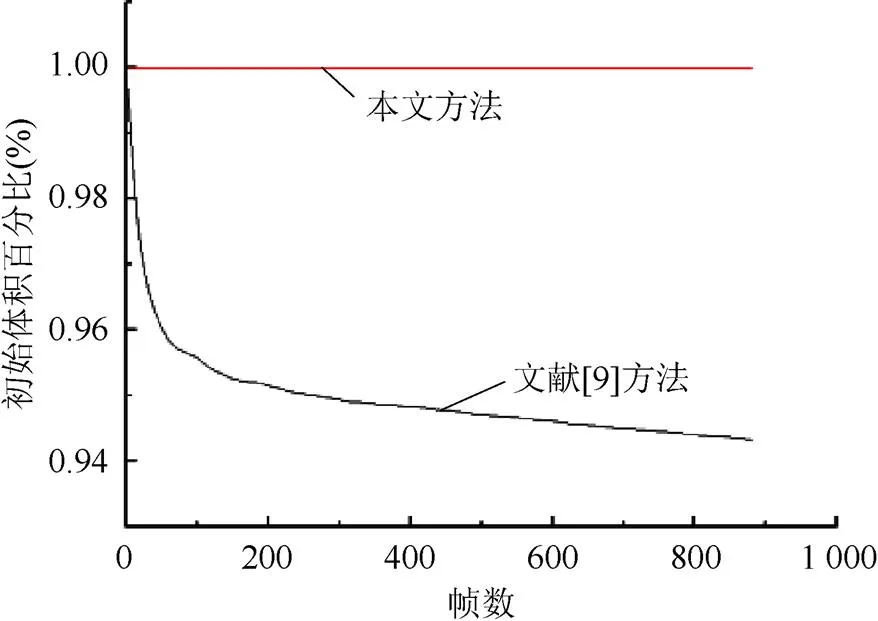
图13 2种方法体积变化对比

4.3 进一步讨论

到目前为止，通过本文方法已经实现了较大时间步长下的实时水体模拟，模拟过程中体积守恒，边界处理令人满意，单向流固耦合效果尚佳。但是水体模拟还有一些更有意思的事情，比如想要在水体的任意位置施加一个力、或者改变任意水体的速度。对于上述用户指定的约束条件，本文方法可以实现。根据浅水方程来看，如果要给水体加上一定的约束条件，那么在每一步模拟的最后，改变水体的速度是最好的选择。外力等其他条件，可以先将其转化为动量通量，再转化为速度的变化。通过该方法，可以更加灵活的模拟水体。图14为本文方法模拟的风对水面的作用力[13]。

图14 风对水面作用

5 结 论

本文提出了一个基于物理的水体模拟模型，该模型能够模拟真实的水面，并且可以进行有效的单向流固耦合，即使在较大的时间步长下也能保持稳定，同时水体在模拟过程始终保持体积守恒。此外，因为基于浅水方程，所以效率很高，可以做到实时模拟。不过，模型的局限性也在于此，只能模拟浅水的无黏流动，对于更复杂的现象无法仿真。尽管如此，本模型在模拟温和的海浪，对体积变化敏感的流体以及流固耦合方面还是可以起到很大的作用。下一步工作是实现双向流固耦合，以及借助粒子的方法使得表面更富有细节且可以模拟一些破碎波浪等现象。

[1] JESCHKE S, WOJTAN C. Water wave animation via wavefrontparameter interpolation [J]. ACM Transactions on Graphics, 2015, 34(3): 1-14.

[2] 房克照, 尹晶, 孙家文, 等. 基于二维浅水方程的滑坡体兴波数值模型[J]. 水科学进展, 2017, 28(1): 96-105.

[3] MICHEL-DANSACV, BERTHON C, CLAINS, et al. A well-balanced scheme for the shallow-water equations with topography or Manning friction [J]. Journal of Computational Physics, 2017, 335: 115-154.

[4] 张迪, 缪小平, 彭福胜, 等. 一种求解对流扩散方程的无条件稳定算法[J]. 水动力学研究与进展: A辑, 2017, 32(2): 158-164.

[5] ROBERT A. A semi-Lagrangian and semi-implicit numerical integration scheme for the primitive meteorological equations [J]. Journalof the Meteorological Society of Japan Ser II, 1982, 60(1): 319-325.

[6] LENTINEM, GRÉTARSSON J T, FEDKIW R. An unconditionally stable fully conservative semi-Lagrangian method [J]. Journal of Computational Physics, 2011, 230(8): 2857-2879.

[7] LENTINE M, AANJANEYA M, FEDKIW R. Mass and momentum conservation for fluid simulation [C]// Proceedings of the 2011 ACM SIGGRAPH/ Eurographics Symposium on Computer Animation - SCA '11. New York: ACM Press, 2011: 91-100.

[8] LAYTON A T, LAYTON H E. A semi-Lagrangiansemi-implicit numerical method for models of the urine concentrating mechanism [J]. SIAM Journal on Scientific Computing, 2002, 23(5): 1526-1548.

[9] LAYTON A T, VAN DE PANNE M. A numerically efficient and stable algorithm for animating water waves [J]. The Visual Computer, 2002, 18(1): 41-53.

[10] HARLOW F H, WELCH J E. Numerical calculation of time-dependent viscous incompressible flow of fluid with free surface [J]. Physics of Fluids, 1965, 8(12): 2182.

[11] QIAN S G, LI G, SHAO F J, et al. Positivity-preserving well-balanced discontinuous Galerkin methods for the shallow water flows in open channels [J]. Advances in Water Resources, 2018, 115: 172-184.

[12] CHENTANEZ N, MÜLLER M. Real-time simulation of large bodies of water with small scale details [C]// Proceedings of the 2010 ACM SIGGRAPH/ Eurographics Symposium on Computer Animation.Goslar: Eurographics Association, 2010: 197-206.

[13] 邹仲水, 赵栋梁, 黄健, 等. 海-气界面动量通量的估计方法分析与应用[J]. 海洋学报:中文版, 2014, 36(9): 75-83.

Real-Time Simulation of Water with Volume Conservation in Large Time Step

ZHU Kui-xin1, GAI Meng2,3, LAI Shun-nan2

(1. Peking University Shenzhen Graduate School, Shenzhen Guangdong 518055, China; 2. School of Electronics Engineering and Computer Science, Peking University, Beijing 100871, China; 3. Beijing Engineering Technology Research Center of Virtual Simulation and Visualization, Peking University, Beijing 100871, China)

Physics-based fluid simulation can capture the movement of water. A common real-time simulation method is based on two-dimensional shallow water equation. Firstly, we introduce the two-dimensional shallow water equation, and then propose a new solution method, which is calculated by an implicit semi-Lagrangian method with volume conservation. This method allows a large time step while maintaining stability. Finally, we add additional correction steps to ensure volume conservation in the calculation process. In addition, a fluid solid coupling method based on momentum conservation is proposed, which works well. The model can simulate water more realistically in real time and ensure that the water volume is always conserved.

shallow water equation; semi-Lagrangian; volume conservation; large time step; fluid solid coupling

TP 391

10.11996/JG.j.2095-302X.2019040725

A

2095-302X(2019)04-0725-08

2019-03-26；

定稿日期：2019-04-26

国家重点研发计划课题(2017YFB1002705)；国家自然基金面上项目(61872398，61632003)；装备预研基金项目(315050501)

朱奎鑫(1997-)，男，河南商丘人，硕士研究生。主要研究方向为流体仿真。E-mail：zkx@pku.edu.cn

赖舜男(1965-)，女，重庆人，工程师，硕士。主要研究方向为虚拟仿真。E-mail：snlai@pku.edu.cn