储备式锂电池锤击激活的流固耦合仿真方法

李向阳，牛兰杰，吕 刚，孙占波

(1.西安交通大学，陕西 西安 710049；2.西安机电信息技术研究所，陕西 西安 710065；3.北京木联能软件股份有限公司西安分公司，陕西 西安 710075)

0 引言

锂和非水无机溶剂亚硫酰氯(SOCl2)组成的无机电解液一次电池，是近年发展起来的新型高能化学电源[1]。民用上，作为一次原电池可广泛应用于通讯、电子、石油勘探、医疗设备等方面[2]。军事上，作为储备式锂电池在美国、以色列、意大利、德国、法国、韩国等部队中有大量的用户群[3-6]。美国已装备引信的化学电源中，储备式锂电池的用量超过了一半。随着国内储备式锂电池研制技术的进步，其应用范围不断扩大。目前，已在无线电引信、机电引信、电子时间引信、修正引信中得到广泛应用。

目前储备式锂电池的激活方式主要有火工品激活、双环境激活、锤击激活、实弹激活等方法[7]。由于储备式锂电池是一次性使用产品，不管以上述哪一种方式激活电池，都会导致电池无法再恢复到原始状态。因此，储备式锂电池最大的一个缺点是每个电池在使用前放电特性不具备可检测性，导致在实施军事打击时整个武器系统有可能无法正常作用，达不到应有的毁伤效果。如何在使用前对储备式锂电池进行可靠性测试，成为一个亟待解决的瓶颈问题。本文提出将ANSYS仿真方法引入到储备式锂电池锤击激活过程中，将激活过程分解成破瓶和进液两个子过程，从而找出储备电池激活过程影响因素，指导以后科研、生产。

1 锤击激活过程及流固耦合方法

1.1 储备式锂电池锤击激活过程

引信用储备式锂电池锤击激活过程，就是指在马歇特锤击机的作用下产生过载，激活机构中的插销开始形变直至断裂，质量块继续运动与玻璃储液瓶发生碰撞，瓶体开始出现裂痕直至完全破碎。插销切断，激活机构(质量块)运动与储液瓶碰撞，电解液迅速流出飞溅到电极处，电池电压建立，从而储备式锂电池被激活。整个激活过程主要包括破瓶过程和进液过程。储备电池内部结构如图1所示。

1.2 ANSYS仿真流固耦合方法

利用ANSYS/LS-DYNA中的流固耦合方法[8-11]对模型进行模拟，耦合系统包括三部分：固体、流体以及流固交界面。固体采用Lagrange算法，流体采用Euler算法，流固耦合方式采用ALE方法来处理相互作用。ALE方法最初出现在数值模拟流体动力学中的有限差分方法中，这种方法兼具有Lagrange方法和Euler方法的特点。它首先在结构边界运动的处理上引进Lagrange方法，因此能够有效跟踪物质结构边界的运动。即可以清晰获知储液瓶的破碎状态和碎片的运动轨迹，并且在流固交界面能够将流体与固体分开计算，再进行数据交换，独立性好。其次，在内部网格的划分上，它吸收了Euler方法的长处，使内部网格单元独立于物质实体而存在，但它又不完全和Euler网格相同，网格可以根据定义的参数在求解过程中适当调整位置，使得网格不至于出现严重的畸变。即在储液瓶破碎的同时，流体无规则流动，网格随时进行自动调整，保证了仿真计算时的稳定性，这种方法在分析大变形问题时非常有效。

图1 储备电池内部结构示意图Fig.1 Schematic diagram of internal structure of reserve battery

1.3 三大守恒方程

储液瓶的破瓶和进液过程在动力学系统上必须满足质量守恒、动量守恒和能量守恒等三大方程[12-13]。其中，质量守恒方程以偏微分方程(即连续方程)的形式给出，因为质量是随时间变化的。

动量守恒方程表示单位时间内流入控制体的动量与作用于控制面和控制体上的外力之和，等于控制体内动量的增加量。

能量守恒方程则表示单位时间内流入控制体的各种能量与外力所作的功之和，等于控制体内能量的增加。

以上三大方程的变量都与时间有关，因此都以偏微分方程形式给出，求解微分形式基本方程，可以得到空间上任何一点的物理量。

2 仿真方法

该方法将储备式锂电池的激活过程分为破瓶和进液两个过程，玻璃储液瓶的破碎属于大变形范畴，由固体控制方程决定；而电解液属于非静止的不可压缩流体，由非静止的不可压缩Navier-Stocks流体控制方程决定。二者在动力学系统上都必须满足质量守恒、动量守恒和能量守恒等三大方程。利用ANSYS/LS-DYNA中的流固耦合方法进行模拟。流固耦合系统包括三部分：固体、流体及流固交界面，固体模型质量块、外壳和储液瓶采用Lagrange算法；流体材料采用ALE算法；流固耦合交界面采用ALE方法来处理相互作用。在马歇特锤击机上给质量块施加过载，通过相互作用，激活机构中的插销开始形变直至断裂；质量块继续运动与玻璃瓶发生碰撞，玻璃瓶开始出现裂痕直至完全破碎。在仿真中很难模拟电极堆中的隔膜吸液过程，因此，我们假定电解液自由扩散到外壳即为进液时间。隔膜完全浸润时间可以通过隔膜本身特性所得。玻璃储液瓶突然破碎后，电解液迅速向四周飞溅，流体矢量指向外壳，过载不同扩散速度也不同。

3 仿真实例和实验验证

3.1 仿真实例

3.1.1 数学模型

为了简化计算模型，采用1/2模型进行模拟，各部分的尺寸根据所选取储备式锂电池尺寸进行建模，模型分为5个部分：质量块、外壳、储液瓶、电解液、空气。node2973是瓶口处选定的一个网络节点。其中，质量块和外壳材料都是不锈钢，储液瓶是1 mm厚GG17玻璃，电解液为亚硫酰氯溶液，流体材料中空气采用空白材料。基本模型通过旋转形成，由于各部分为不规则结构，因此网格采用V-SWEEP方法进行划分。所建网格模型图2所示。

图2 网格模型Fig.2 Mesh model

3.1.2 破瓶过程

分别在6 000g、10 000g的过载下，选取0.000 6 s和0.001 2 s两个时间节点考察玻璃储液瓶破碎情况，观察玻璃碎块大小。

图3所示为储液瓶不同时间，不同过载破瓶情况。由图3可以看出，储液瓶开始破碎时间很快。在同一个时间点，过载10 000g比6 000g破瓶更好，随着过载值的增大，储液瓶破碎的更完全，更有利于激活时间的减少。6 000g过载在两个不同时间节点，破碎情况变化不大；而10 000g过载在两个不同时间节点，破碎情况变化大，玻璃碎块更小，更有利于激活时间的降低。因此， 6 000g过载明显偏低，不利于激活时间的降低；10 000g以上过载玻璃碎块很小，有利于激活时间的降低。

图3 储液瓶不同时间不同过载破瓶情况Fig.3 Reservoir broken at different time and different overload

为了更好地说明问题，我们选取玻璃瓶口处2973节点为研究对象，在激活过载分别为6 000g和10 000g时，单独考核其在整个破瓶过程中速度随时间的变化关系。不同过载下节点2973速度时间关系如图4所示。

从图4可以看出：初始破瓶阶段，节点速度迅速上升。在10 000g过载下，节点达到速度峰值31.85 m/s，时间为0.2 ms，对应着完全破瓶点，1.2 ms后速度趋于平稳状态； 6 000g过载下，节点达到速度峰值12.87 m/s，时间为0.4 ms，对应着完全破瓶点，2.6 ms后速度趋于平稳基本为零。在16 ms处，节点速度突然升高到15 m/s以上，这可能是节点在其他碎块的碰撞下，又获得了一定的速度所致。

图4 不同过载下节点2973速度时间关系Fig.4 Relation between velocity and time of node 2973 at different overload

很显然，节点2973在10 000g过载下的速度峰值和速度稳定平台所对应时间远低于6 000g过载。说明10 000g过载更有利于降低激活时间。

3.1.3 进液过程

在6 000g和10 000g锤击过载下，分别模拟电解液进液过程，考察进液时间大小。

图5 不同过载下进液情况Fig.5 Liquid inlet at different overload

由图5可以看出，在6 000g和10 000g两个不同激活过载下，电解液完全充满电极腔体所需时间分别是4.12 ms和1.96 ms，进液时间随激活过载增大而明显减小。

再结合该模型下隔膜被电解液完全浸润所需时间大概为6 ms，因此，10 000g过载下总激活时间为9.16 ms；6 000g过载下总激活时间为12.72 ms。综合考虑破瓶过程和进液过程，所选模型在6 000g过载下破瓶碎块偏大，进液偏慢；而在10 000g过载下破瓶碎块很小，进液很快。再结合引信电源快激活的特点，认为6 000g及以下的激活过载，不利于该模型的激活过程；10 000g及以上的激活过载，有利于整个激活过程。

3.2 实验验证

为了验证仿真结果的准确性， 在仿真值和实验值相近的条件下， 根据仿真模型设计了储备式锂亚硫酰氯电池原理样机，设计的试验电池为单元电池结构，开路电压3.65 V。常温，在马歇特锤击机上分别以6 000g、10 000g的过载激活，微安级小电流放电，接8861-50电池测试仪，记录放电曲线如图6所示。

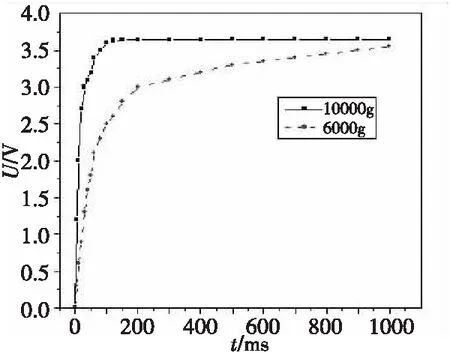
图6 锤击激活放电曲线Fig.6 Discharge curve of hammer activation

从图5和表1可以看出，储备式锂电池分别以6 000g和10 000g的过载激活时，电池电压达到2.0 V的激活时间分别是58 ms和9.6 ms。再结合引信电源快激活的使用特点，说明6 000g的激活速度较慢，不利于储备式锂电池的快速激活；10 000g的激活速度很快，有利于储备式锂电池的快速激活。因此，10 000g及以上的激活过载都有利于该模型所对应的储备式锂电池快速激活。

表1 不同过载下激活时间仿真值和实测值对比表

表1中10 000g过载下激活时间仿真值和实测值非常接近；6 000g过载下二者差别较大。主要是由于整个激活过程太复杂，在仿真模拟时进行了一定程度的简化以及所选取的仿真条件更接近于10 000g的实际过载所致。这说明10 000g及以上的激活过载有利于该模型所对应的储备式锂电池快速激活，6 000g及以下的激活过载不利于该模型所对应的储备式锂电池快速激活。因此，可根据不同的电池模型进行不同的仿真计算，从而弥补了储备式锂电池在使用前放电特性不可检测的缺憾，在一定程度上提高了储备式锂电池作用可靠性。

4 结论

本文提出了储备式锂电池锤击激活过程ANSYS仿真方法。该方法将储备式锂电池的激活过程分为破瓶和进液两个过程，利用ANSYS/LS-DYNA中的流固耦合方法进行模拟，固体模型质量块、外壳和储液瓶采用Lagrange算法，流体材料采用ALE算法，流固耦合方式采用ALE方法来处理相互作用。仿真模拟出6 000g过载激活时储液瓶碎块较大、进液时间偏慢，不利于该模型下的储备式锂电池快速激活；而10 000g过载激活时储液瓶碎块较小、进液时间很快，有利于该模型下的储备式锂电池快速激活。仿真值与实测值进行对比，在10 000g过载下二者接近，而6 000g过载下二者差别较大，表明10 000g及以上的激活过载有利于该模型所对应的储备式锂电池快速激活，6 000g及以下的激活过载不利于该模型所对应的储备式锂电池快速激活。因此，可根据不同的电池模型进行不同的仿真计算，从而弥补了储备式锂电池使用前放电特性不可检测的缺憾，在一定程度上提高了储备式锂电池作用可靠性。