燃机叶片U带肋冷却通道的结构优化

龚建英，高铁瑜，吴伟烽，李 真

（西安交通大学能源与动力工程学院，陕西西安710049）

1 引言

20世纪以来，随着科学技术的发展和进步，航空发动机和地面燃气轮机在工程实际当中的应用越来越广泛，如何提高燃气轮机的效率逐渐受到人们的重视[1]。研究表明，燃气温度是决定燃气轮机主要性能的一个重要参数，冷却技术的不断进步成为提高此温度的关键技术[2]。

内部对流冷却是燃气轮机叶片冷却的重要组成部分之一[3]。这种冷却方式将压气机压缩过的高压空气由叶根处引入叶片内部冷却通道，通过高压空气和通道壁面的换热实现冷却作用。为了提高换热效率，先进的燃气轮机广泛采用了在位于叶片吸力面和压力面一侧的通道壁面放置肋片或柱状肋片的强化换热措施[4]。

在实际燃气轮机叶片中，为了简化内部结构，往往将不同的带肋直通道首尾相连，形成复杂的U形带肋通道。此时，180°弯头对于上下游流动和传热的影响不能忽略，针对这一问题，国内外学者进行了大量的研究。Han和Zhang[5]用实验的方法研究了U形转角和肋片方向对三流程通道中流动和换热的影响。Erelli等[6]用实验和数值模拟的方法研究了不同U形转角形状对于光滑U形通道中流动和换热的影响。结果显示转角处的二次流越强，当地换热强化能力越大。角外侧壁为90°直角连接，内侧壁为半圆形时换热效果最好，内外侧壁面都为90°直角连接时换热效果最差。Howoong等[7]对光滑U形冷却通道的半圆形弯头形状进行了优化。薛兴旭[8]对实际燃气轮机动叶进行了优化和改进。Dieu等[9]基于NUMECA建立了优化平台，对2种带肋单通道和一种U形通道分别进行了参数化建模和优化设计。优化结果比初始结构在平均换热系数上分别有12%和23.4%（单通道），12.8%（U形通道）的提高。

研究表明，斜置肋片和180°弯头导致的二次流动是造成带肋通道内强化换热的决定性因素。由此可推知，采用带肋U型通道的结构可获得较好的强化换热效果，但是目前极少有针对带肋U型通道的结构优化研究。文献已证明，影响带肋U形通道下游直通道换热和阻力特性的主要因素是两直通道中的肋片角度和肋片方向组合[10-11]。基于此，本文使用代理模型和遗传算法，对带有直肋的U形通道的肋片角度，肋片方向和肋片相对位置进行寻优计算，以其得到一种新的强化传热设计，改善整个通道的换热和流动性能。

2 优化方法

2.1 优化流程

为了同时兼顾计算精度和计算效率，采用基于代理模型的优化设计方法对带肋通道模型进行优化设计，优化设计流程图和ANSYS Workbench优化设计平台如图1所示。如图1（a） 所示，优化流程主要分为4个步骤：

（1） 根据各个优化变量的取值范围，采用拉丁超立方（LHS）设计方法确定由各个优化变量构成的优化空间内的样本点集；

（2） 以样本点集为设计点，通过参数化建模实现模型的构建，采用CFD方法对不同设计点下的响应进行计算；

（3） 基于Kriging代理模型，根据计算获得的样本处响应数据，对样本集的响应面最优逼近；

（4）使用遗传算法对响应面寻优。

图1（b） 所示为ANSYS Workbench平台。优化平台由3部分组成：参数化建模、CFD计算和响应面优化。

其中，参数化建模采用ANSYS Design Modeler模块完成，CFD计算的网格划分和计算采用ANSYS Workbench中的Fluid Flow模块完成，响应面优化模块包括实验设计，响应面和优化3个子模块，各模块由系统自动进行调用。

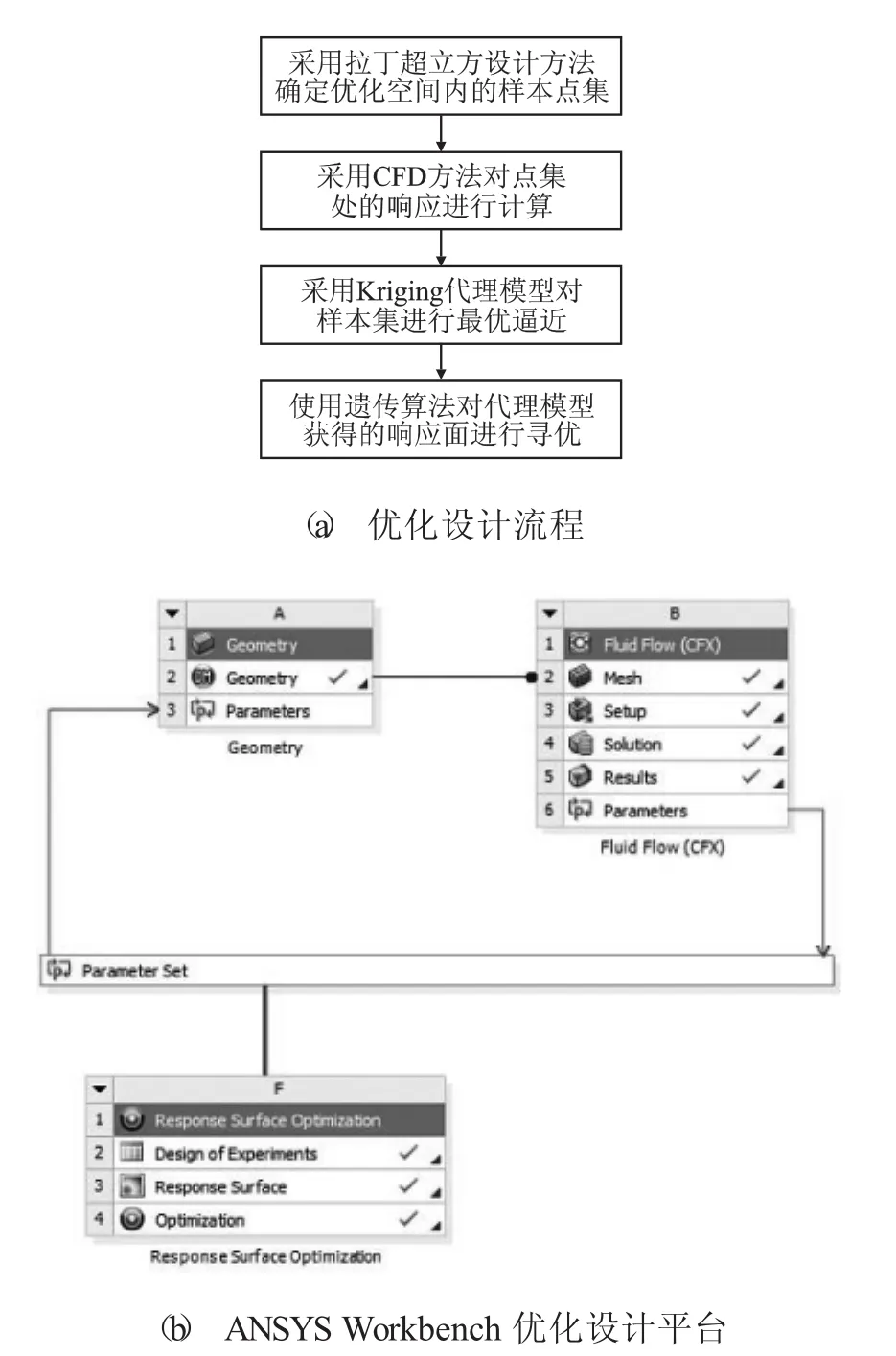
图1 优化设计方法

2.2 几何模型与优化设计变量

斜置直肋片的几何模型与优化变量如图2所示，为减少计算量，在通道中分面处采用对称边界的条件。肋片高度为4 mm，肋片间距为40 mm。通道截面宽44 mm，通道进口面到弯头端壁总长度为440 mm，两直通道之间横向距离为44 mm。4个优化变量分别为：第一直通道肋片与流动方向夹角A26；第一直通道第一根肋片中点与进口面距离H10；第二直通道最后一根肋片与出口面之间距离H11和第二直通道肋片与流动方向之间夹角A27。

2.3 计算设置

采用非结构四面体网格，近壁面采用20层边界层网格进行加密，以保证湍流模型对近壁面网格的要求，壁面Y+值小于1，总网格点数为305万。

设置流体域参考压力一个大气压，进口设置静压0 Pa，静温298 K，进口湍流度5%，出口面设置质量流量边界，保证进口雷诺数为30000，壁面为无滑移等壁温边界，壁温为338 K，通道中分面采用对称边界。

为验证不同湍流模型在U形带肋通道中的计算精度，进行了数值模拟，第1流程，第2流程的带肋壁面区域平均努塞尔数比随不同湍流模型的变化如表1所示，并与实验值进行了比较，结果显示湍流模型对换热和阻力的计算结果均存在显著的影响。对于通道摩擦因子而言只有SST湍流模型的结果与实验值差别较小。对于带肋壁面的区域平均努塞尔数比，第1流程的计算结果依然是SST湍流模型与实验值最接近；而LLR湍流模型在弯头区域的计算结果具有最小的相对误差；对于第2流程，k-ε和RNG k-ε以及SST湍流模型都具有较高的计算精度。此外，Farisco[12]以及Walker[13]的研究也表明SST模型在U形光滑通道中具有最优的计算精度。综上所述，选定SST湍流模型作为本文中U形带肋通道数值模拟的数学模型。

优化计算采用Kriging代理模型生成响应面，采用遗传算法对进行寻优。优化变量为A26∈ [30°，150°]，A27∈ [30°，150°]，H10∈ [0.04，0.12]，H11∈ [0.04，0.12]，其中单位m。优化指标为第一直通道总换热功率，第二直通道总换热功率和通道摩擦因子。最大帕累托效率为70%。

2.4 数据处理

通道进口雷诺数定义如下

式中Re——雷诺数

ρ——工质密度，kg/m3

Dh——通道的水力直径，m

μ——为工质的动力粘性系数，m2/s

V——为进口面的平均速度，m/s

当地努塞尔数的定义如下

式中Nu——努塞尔数

k——流体导热系数，W/m·K

Tw——壁面温度，K

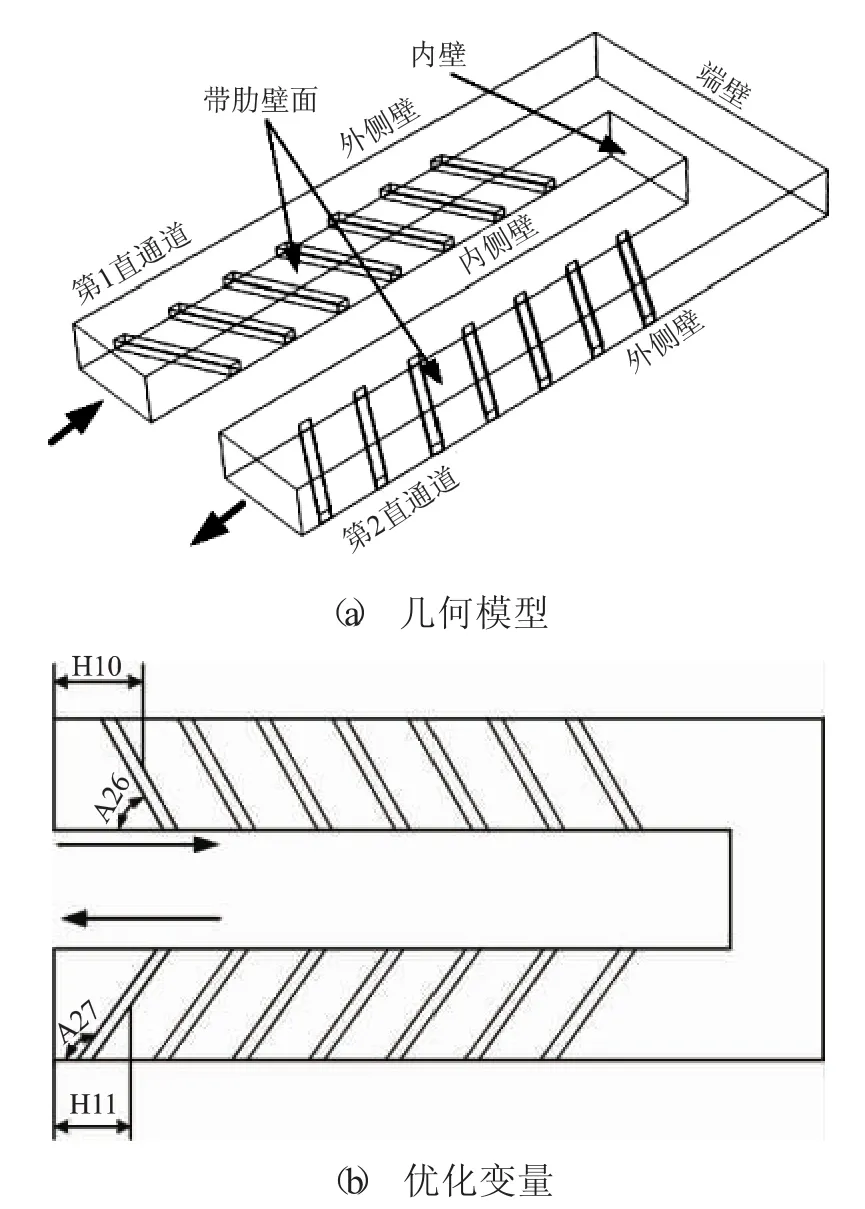
图2 带肋U形通道的几何模型与优化变量

表1 U形带肋通道湍流模型验证（Re=30000）

Tb——流体定性温度，K

q——通道热流密度，W

摩擦因子的定义如下

式中f——摩擦因子

Δp——通道流动压降，Pa

l——流动距离，m

换热性能因子

式中f0——光滑管道摩擦因子

3 结果与分析

图3所示为通道整体摩擦因子与单个优化变量之间的响应面。针对肋片角度这一变量，在第1直通道，随着肋片与流动方向夹角的增大，摩擦因子逐渐增大，但是增长幅度逐渐放缓，在A26=110°时达到最大，随后下降；对于第2直通道，摩擦因子随着A27的增大先增大后减小，最大值位于A27=80°时。肋片相对位置对摩擦因子的影响与肋片角度不同，摩擦因子随着H10的增大先增大后减小，峰值出现在H10=0.085 m附近；随着H11增大，摩擦因子减小，最小值位于H11=0.12 m处。

图4所示为摩擦因子分别单独受到2个直通道中的优化变量影响的响应面。由图可知，对于第1直通道，响应面形状与图3（a）中的类似，且H10对摩擦因子的影响明显强于A26。而第2直通道中，A27和H11对摩擦因子的影响都比较明显，其中A27的影响程度强于H11。

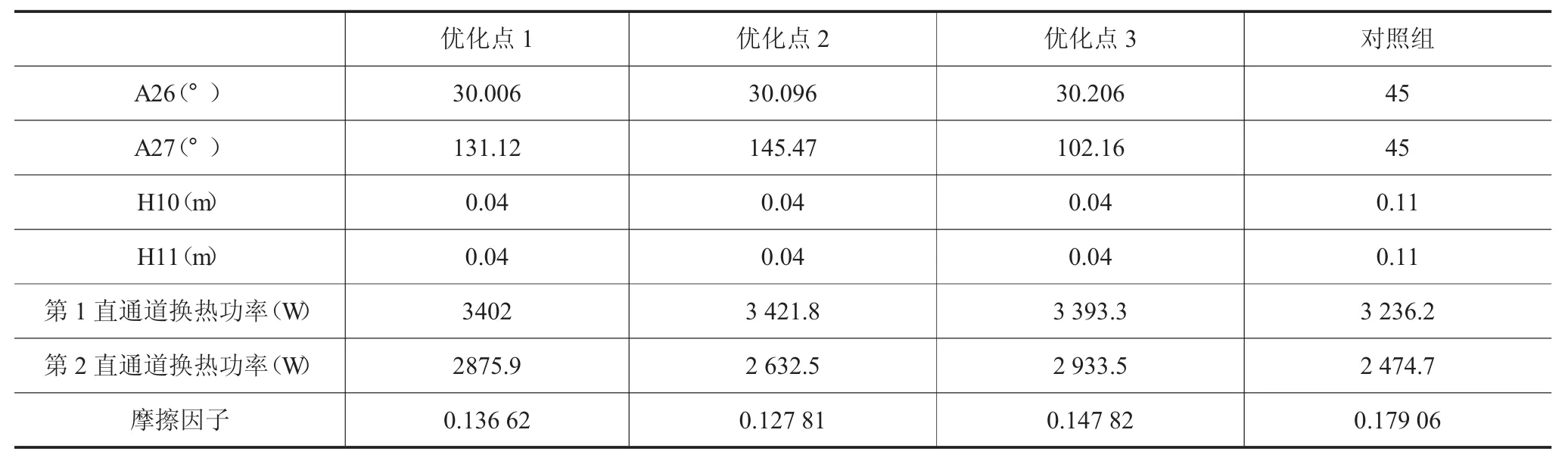
表2 带肋U形通道优化结果

图5所示为第一直通道带肋面换热功率与第1直通道优化变量响应面。可以看出第1直通道带肋面换热功率的响应面呈现明显的马鞍形，肋片角度位于区间两端，H10位于0.06~0.07 m时换热功率最大。

图6所示为第2直通道带肋面换热功率与两直通道中肋片角度的响应面。可以看出A27对第二直通道带肋面换热功率的影响呈现明显的的M形分布，换热功率的极大值分别位于A26取值区间的两端以及A27=130°和50~60°之间。

图7所示为第二直通道带肋面换热功率与两直通道中肋片相对位置的响应面。可以看出肋片相对位置对第二直通道带肋面换热功率的响应面呈现明显的马鞍形。当H10位于取值范围的中段，H11位于取值范围的两端时第2直通道带肋面换热功率最高。

图8所示为第2直通道带肋面换热功率分别受到第1和第2直通道影响时的响应面。可见第1直通道对第2直通道换热性能影响的响应面同样呈现马鞍形分布，A26取值在区间两端，H10取值在区间中段时第2直通道换热性能较好。第2直通道本身的参数对当地换热功率的影响同样明显，其中A27对于第2直通道带肋面换热功率的影响呈现明显的M形分布，A27在60°附近和130~140°区间都存在明显的功率峰值。而H11对第二直通道带肋面换热功率的影响没有A27明显，随着H11增大，换热功率先减小后增大。

表2为带肋U形通道的优化结果。对照组2个直通道中肋片角度均为45°，H10和H11均为0.11 m，即肋片相对更靠近弯头。优化结果显示当肋片距离弯头较远时，直通道的换热功率最高。摩擦因子最低的优化点是优化点2，比对照组降低了28.6%，其他2个优化点的摩擦因子分别比对照组低23.7%和17.4%。第二直通道换热功率最高的是优化点3，比对照组提高了18.5%。其他2个优化点分别比对照组提高了16.2%和6.37%。

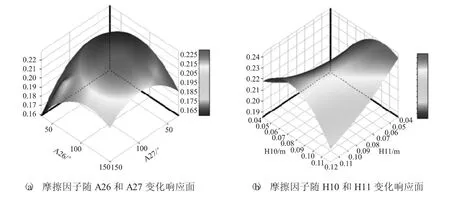
图3 摩擦因子与单个优化变量关系响应面

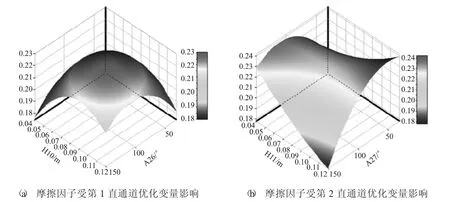
图4 摩擦因子受2个直通道中优化变量影响的响应面

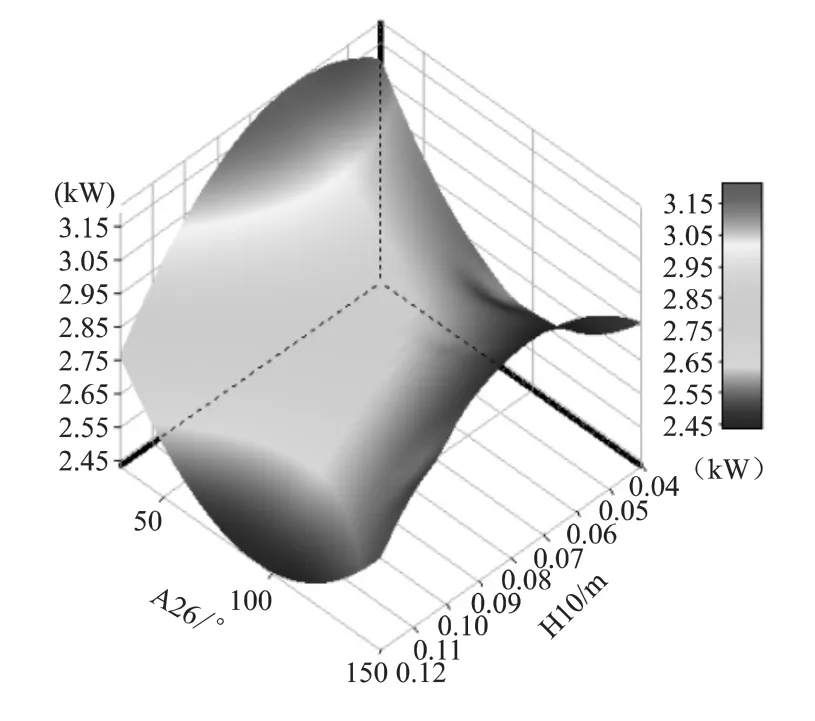
图5 第1直通道带肋面换热功率与第1直通道优化变量响应面

图6 第2直通道带肋面换热功率与两直通道中肋片角度的响应面

4 结论

本文利用Kriging代理模型和遗传算法基于ANSYS Workbench软件平台构建了优化设计平台，利用U形通道中主流区域二次流在2个直通道和弯头中的流动和能量传递特点，对2个直通道中的肋片角度、肋片的相对位置进行了优化计算。结果表明：

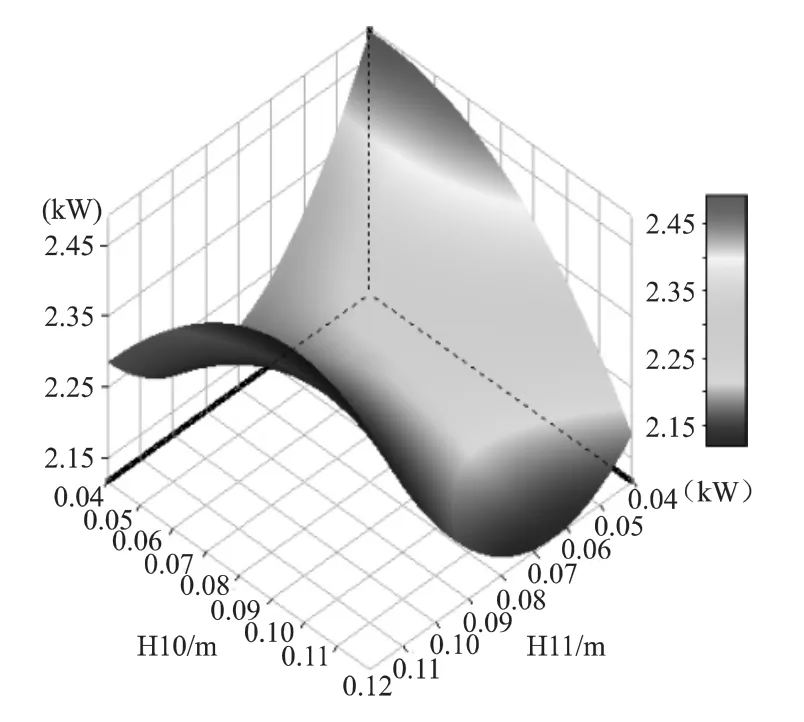
图7 第2直通道带肋面换热功率与两直通道中肋片相对位置的响应面

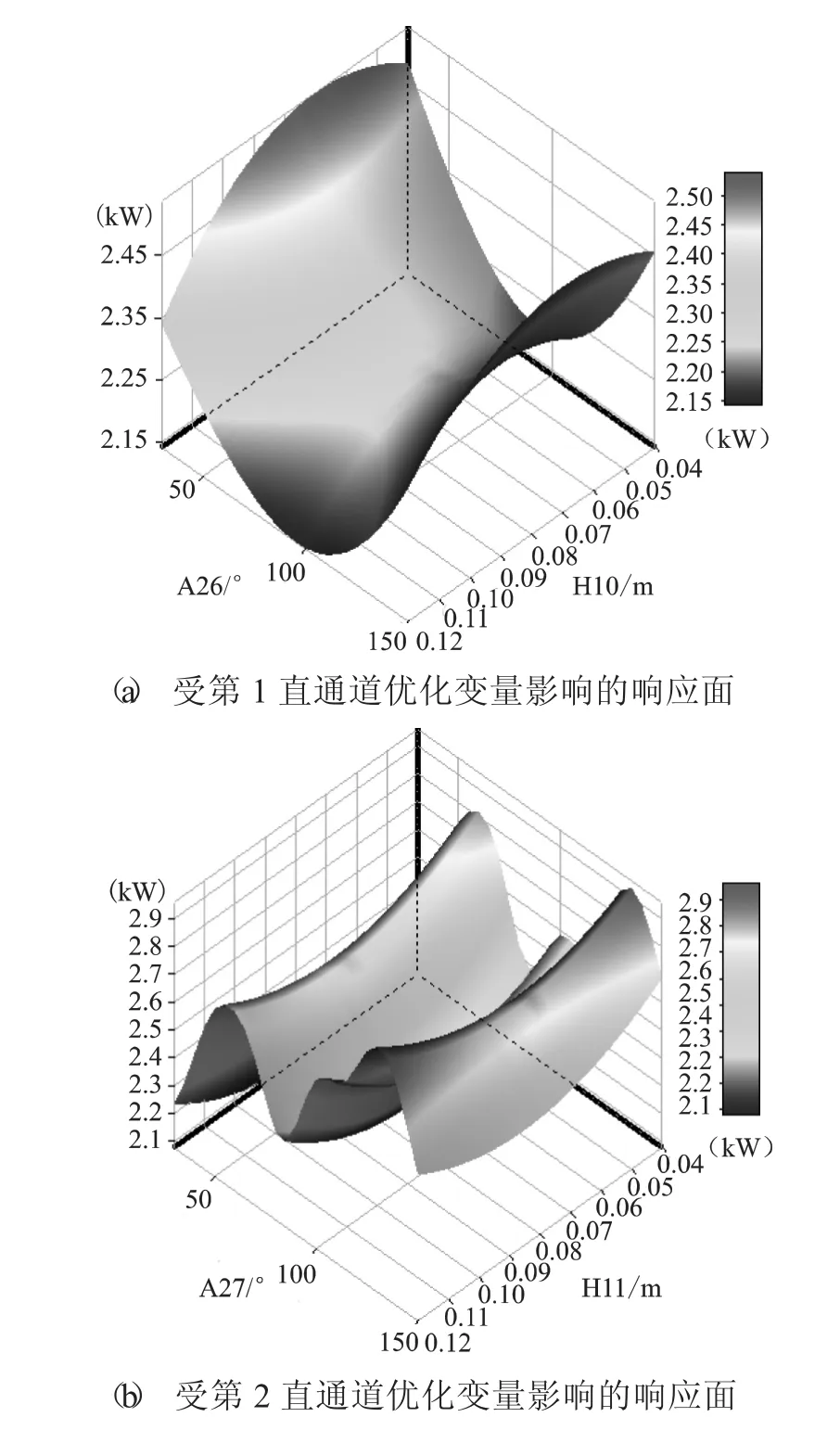
图8 第2直通道带肋面换热功率受2个直通道中优化变量影响的响应面

（1） 在通道冷却结构设计中，第1、2直通道内的肋片角度和肋片方向均对下游第2直通道中的换热效果和整个通道的流动阻力有明显的影响。

（2） 相比于对照通道，第2直通道换热功率最高提高了18.5%，摩擦因子最大降低幅度为28.6%。

（3）相邻直通道中的肋片角度和相对位置应独立进行考虑，特别是第2直通道中的肋片角度和相对位置，应与第1直通道的肋片参数相匹配。