磁极优化降低表贴式永磁电机电磁振动噪声

黄厚佳，徐余法,2，李全峰,，黄苏融

(1.上海电机学院，上海 201306；2.上海第二工业大学，上海 201209;3.上海大学，上海 200072)

0 引 言

振动和噪声(以下简称为振动噪声)是衡量电机性能的一项重要技术指标。随着对环境保护和电机性能要求的不断提高，电机振动噪声水平已成为影响其在市场上竞争的重要因素[1]。电机运行过程中会产生交变径向电磁力并作用在定子铁心上，从而使定子铁心及相关机械部件产生电磁振动，向空气中辐射电磁噪声。电磁振动噪声是电机振动噪声的重要来源，因此削弱电机电磁振动噪声对提高电机性能具有重要意义。

对于电机电磁振动噪声问题，国内外学者进行了大量研究。文献[2]采用机电类比法，系统介绍了感应电机、同步电机和直流电机的振动噪声分析和计算过程。文献[3-4]深入分析了径向电磁力波幅值、阶次和频率特性，但并未指出对电机电磁振动噪声影响较大的关键力波分量。文献[5-6]建立了定子系统固有模态分析模型，考虑了绕组、浸漆以及机壳端盖对定子系统的影响，提高了计算精度。文献[7-9]研究了不同极槽配合对永磁电机齿槽转矩和振动噪声特性的影响，指出具有低齿槽转矩的极槽配合可能使电机产生较大的振动噪声，但尚未分析产生这种现象的原因。文献[10]研究了变频器供电对永磁同步电机振动噪声的影响，得到因变频器供电而产生的对电机振动噪声影响较大的关键力波分量。

随着计算机技术的发展，基于有限元的多物理场耦合分析模型被越来越多地应用于电机电磁振动噪声的预测和分析。文献[11-14]系统介绍了电机多物理场耦合振动噪声模型的建立及分析过程，较大提高了电机振动噪声预测和分析的准确性，但会耗费大量计算时间。基于上述缺点，文献[15]结合限元法和解析法，建立了电机多物理场耦合振动噪声分析模型，在保证具有较高精度的同时缩短了计算时间。

极弧系数与磁极偏心距是表贴式永磁电机的重要设计参数，目前针对极弧系数及磁极偏心距对表贴式永磁电机电磁振动噪声影响的研究较少。文献[16-17]提出运用磁极偏心削弱电机电磁激振力波的方法，得到主要电磁力波分量随磁极偏心距和极弧系数的变化规律，但并未深入研究两者对电机电磁振动噪声的影响。

本文首先运用解析法建立磁极偏心时径向气隙磁密模型，根据解析模型运用快速傅里叶变换，然后编写出各阶磁密谐波幅值计算程序，以一台4.2 kW表贴式永磁电机为例，计算出不同磁极偏心距和极弧系数下的电磁振动噪声，最后得到磁极偏心距和极弧系数对表贴式永磁电机电磁振动噪声的影响规律。

1 磁极偏心时径向气隙磁密建模

当磁极未偏心时，表贴式永磁电机磁路模型如图1所示。忽略定转子磁压降，空载气隙磁通密度可表示[18]：

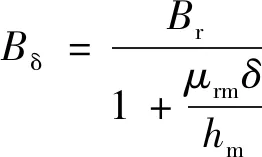
(1)

式中：Br为永磁体剩余磁通密度；μrm为永磁体相对磁导率；δ为气隙长度；hm为永磁体磁化方向长度。

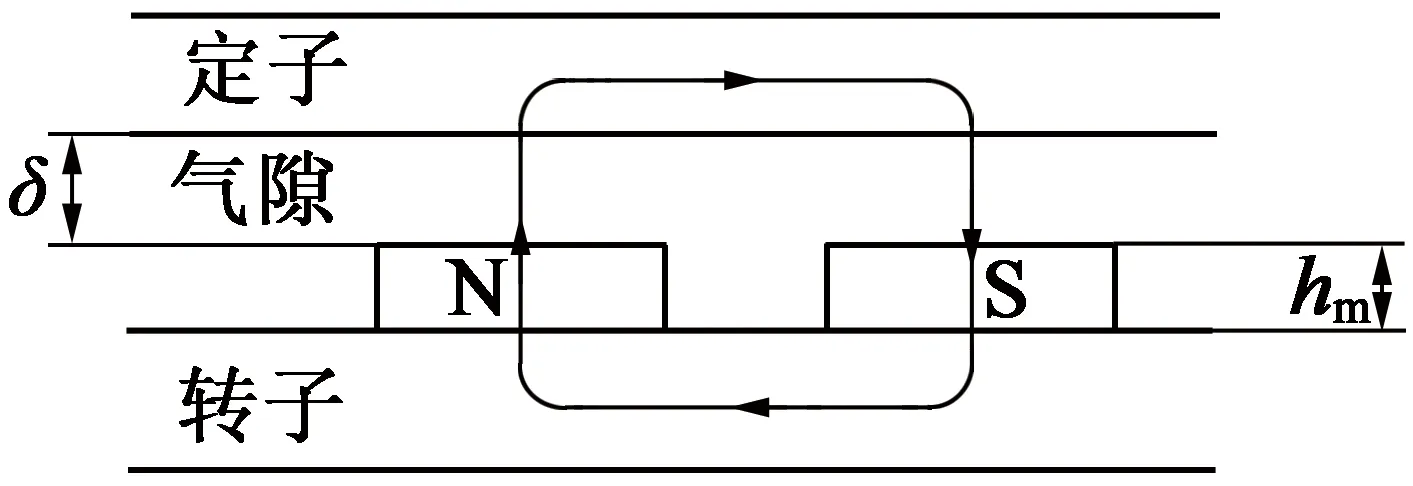
图1 表贴式永磁电机磁路

图2表示磁极偏心距为e时的永磁体结构。R1为磁极中心处永磁体半径，R2为转子外径，hm为磁极中心处永磁体磁化方向长度，h为偏离磁极中心θ角度处的永磁体磁化方向长度。设电机极对数为p，极弧系数为αp，则θ的取值范围为[-παp/(2p),παp/(2p)]。

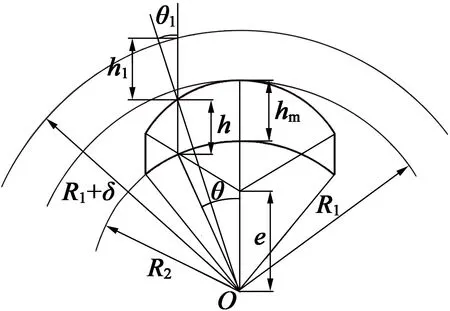
图2 偏心磁极永磁体结构

根据图2，在偏离磁极中线θ角度处永磁体的磁化方向长度可表示：

(2)

由于永磁体磁导率近似等于空气，可假设气隙中磁通密度方向与永磁体磁通密度方向一致，则在偏离磁极中线θ角度处，气隙磁路长度h1可表示：

忽略定子开槽对气隙磁密的影响，根据式(1)，磁极偏心后偏离磁极中心θ角度处气隙磁通密度可表示：

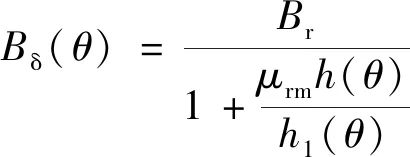
(4)

因此，偏离磁极中线为θ的位置，径向气隙磁通密度可表示：

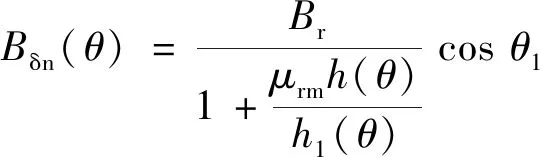
(5)

由于式(5)的径向气隙磁密表达式较为复杂，无法直接对其进行傅里叶变换求取各阶谐波的幅值，可根据上述表达式运用离散傅里叶变换，并编写相应MATLAB程序求取各阶磁密谐波幅值。

以一台4.2 kW永磁电机为例，运用所编写的程序对不同磁极偏心距和极弧系数下的径向气隙磁密进行计算，研究二者对径向气隙磁密的具体影响。电机主要参数如表1所示。图3为极弧系数为0.8和0.925，磁极偏心距从0～18 mm变化时各阶径向气隙磁密谐波幅值随磁极偏心距的变化情况。

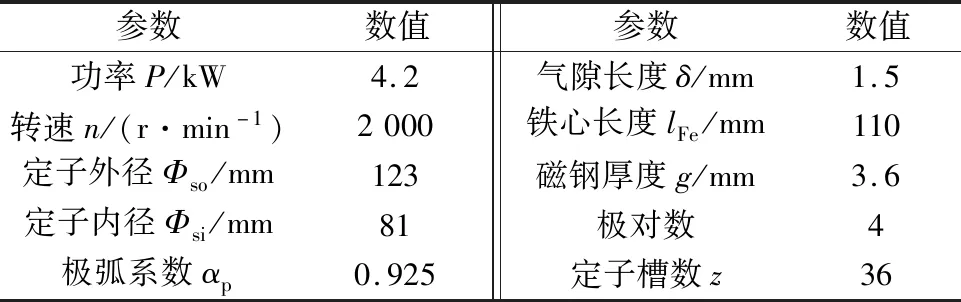
表1 电机参数

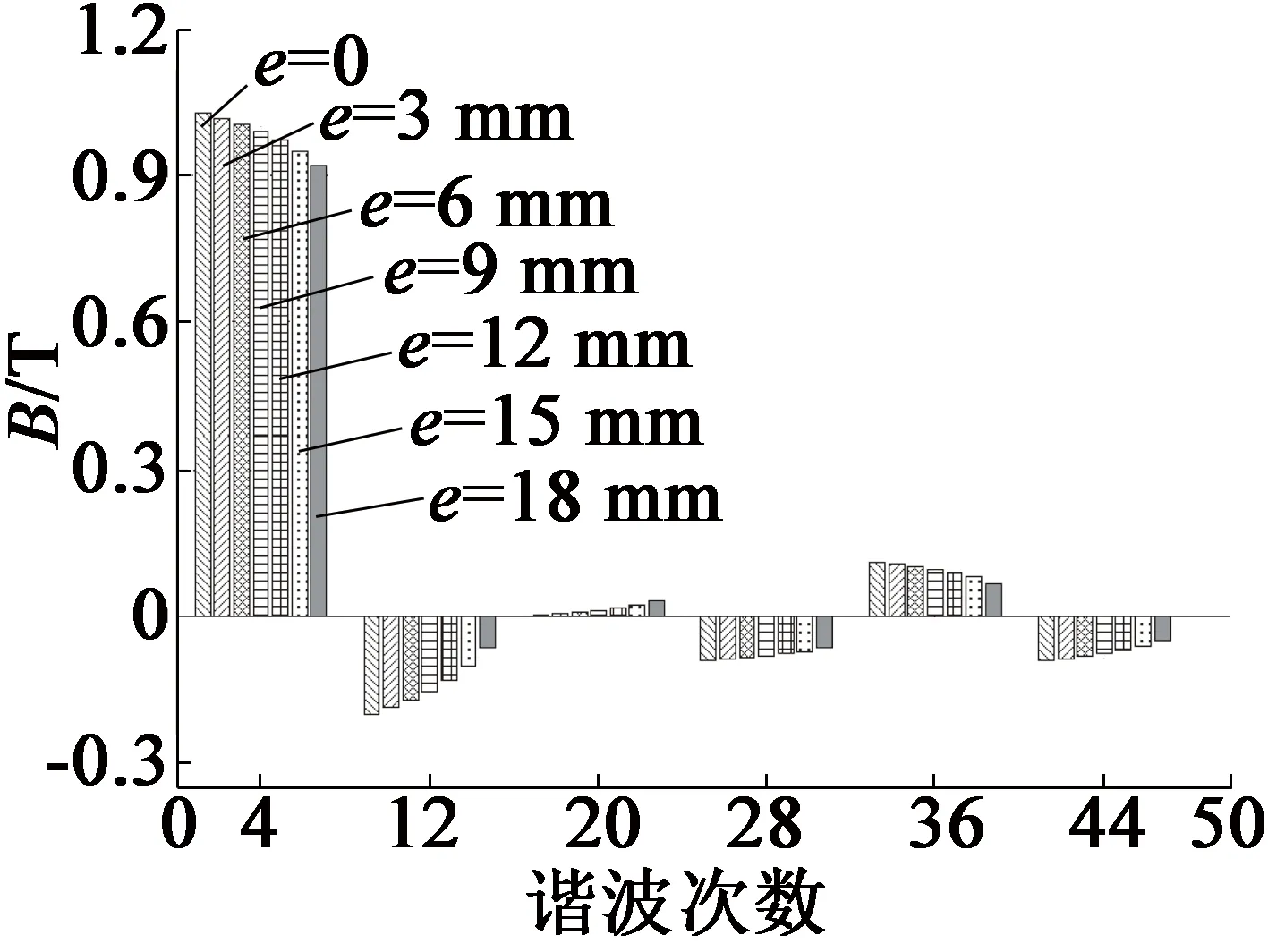
(a) αp=0.8

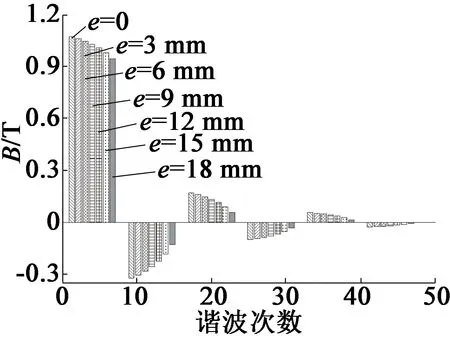
(b) αp=0.925

从图3中可以看出，磁极偏心距对径向气隙磁密谐波的影响与极弧系数有关。例如当极弧系数αp为0.8时，20阶径向气隙磁密谐波幅值随着磁极偏心距增大而变大；但当极弧系数αp为0.925时，该次谐波幅值随着磁极偏心距增大而减小。从图3中还可以看出，通过调整极弧系数可以使某阶气隙磁密得到较大削弱，如20阶、44阶磁密谐波。因此，为了削弱电机电磁振动噪声，要同时考虑极弧系数和磁极偏心距的影响，选取二者合适的组合值，使电机电磁振动噪声降到最低点。

2 径向电磁力波解析模型

电机电磁振动噪声产生的根源主要为作用在定子铁心上的径向电磁力。由麦克斯韦张量方程可知，作用在单位气隙面积上的径向电磁力[19]可表示如下：

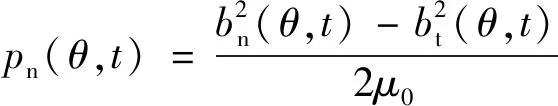
(7)

式中：bn(θ,t)为径向气隙磁密；bt(θ,t)为切向气隙磁密；μ0为真空磁导。与径向气隙磁密相比，切向气隙磁密可以忽略不计，单位气隙面积径向电磁力又可表示：

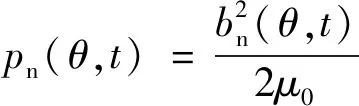
(8)

忽略铁心饱和的影响，气隙磁动势与单位面积气隙磁导相乘可得径向气隙磁密：

bn(θ,t)=f(θ,t)λ(θ,t)

(9)

式中：f(θ,t)为气隙磁动势;λ(θ,t)为单位面积气隙磁导。

同步电机在空载和负载运行时电磁噪声中主要成分的频率和阶数都是不变的，从空载到负载运行时，同步电机电磁噪声和振动的主要频率成分的声压级、声功率级或振动级改变值[2]：

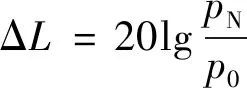
(10)

式中：pN为空载时同步电机的某一主要力波成分；p0为负载时同步电机的某一主要力波成分。

因此，知道电机空载运行时的电磁振动噪声可以估算出电机负载运行时的振动噪声。本文重点分析磁极偏心距及极弧系数对电机空载运行时电磁振动噪声的影响。

忽略电机空载运行时电枢电流的影响，以电枢周长2pτ作为基准波长，气隙磁动势可表示：

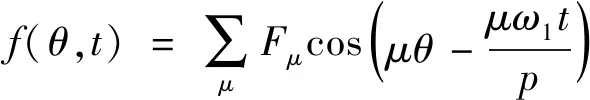
(11)

式中：p为极对数；μ为磁动势空间阶次，μ=(1,3,5,7，…)p。假设气隙磁导只受定子开槽的影响。单位面积气隙磁导可表示：

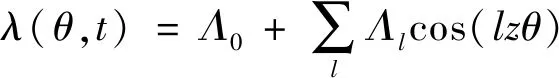
(12)

式中：Λ0为磁导不变分量；Λl为磁导l次谐波分量幅值；z为定子槽数。Λ0和Λl的计算可参考文献[20]，在此不再赘述。以δ/μ0作为基准磁导，磁导标幺值可表示：

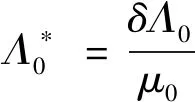
(13)

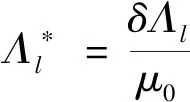
(14)

将式(11)、式(12)代入式(9)，可得到电机空载运行下径向气隙磁密表达式：

式中：

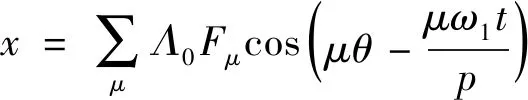
(16)

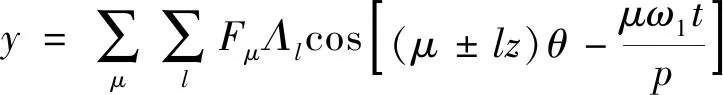
(17)

将式(15)代入式(8)可求得径向电磁力波表达式：

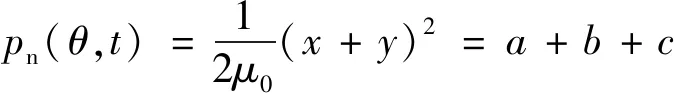
(18)

式中：a为主极磁场相互作用产生的径向电磁力波；b为主极磁场与齿谐波磁场相互作用产生的径向电磁力波；c为齿谐波磁场相互作用产生的径向电磁力波。由于c项力波分量幅值很小，产生的振动噪声可以忽略不计，因此仅考虑a,b两项，a和b表达式分别如下：

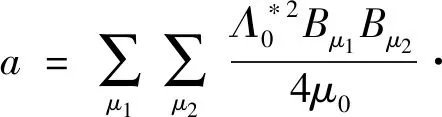
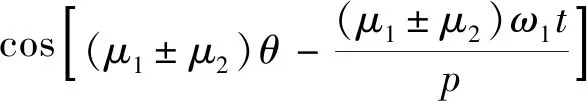
(19)

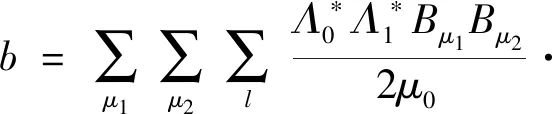
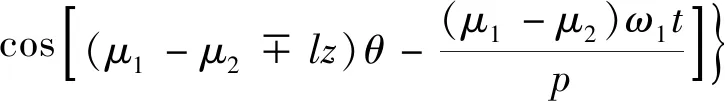
(20)

在众多径向电磁力波分量中，对电机电磁振动噪声起决定作用的主要为空间阶次较低、幅值较大的力波分量。由于定子铁心变形量与力波空间阶次的四次方成反比[2]，高阶力波所激发的电磁振动噪声较小，一般仅考虑阶次小于等于4的力波分量所产生的电磁振动噪声。式(19)中主磁场基波产生的径向电磁力波(用pn1表示)和式(20)中主磁场与一阶齿谐波相互作用产生的径向电磁力波(用pn2表示)，由于幅值较大，因此pn1，pn2中阶数小于4的力波分量对电机振动噪声起着决定作用。根据式(19)和式(20)，pn1，pn2分别如下：

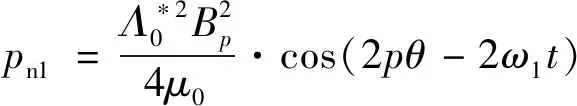
(21)

当电机极对数大于2，且固有频率远大于基波电流频率的2倍时，磁场基波产生的径向电磁力波阶数较高，且频率远离电机固有频率，此时力波激发的电磁振动噪声较小，可仅考虑pn2对电机振动噪声的影响，例如车床用小型永磁伺服电机。除此之外，要同时考虑pn1，pn2对电机振动噪声的影响。

3 磁极偏心距和极弧系数对电机电磁振动噪声的影响

根据文献[1]，忽略阻尼和机壳的影响，设定子轭的单位表面质量为m(m包含绕组质量)，定子系统柔度为λ，当定子受到周期性交变电磁力作用时，其振动微分方程：

(23)

式中：y为振动位移；ω为力波频率；pnav为定子平均半径圆柱表面上单位径向力幅值，其表达式：

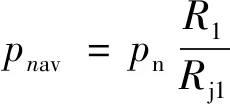
(24)

式中：R1，Rj1分别为定子内圆半径及定子轭半径；pn为作用在定子内径上单位面积径向电磁力波幅值。

由式(23)可解得定子振动时速度和加速度幅值，其表达式分别如下：

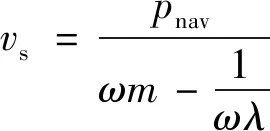
(25)

(26)

由振动引起的噪声声强：

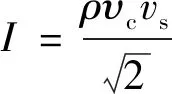
(27)

式中：ρ为空气密度；υc为声波在真空中的传播速度。声强有效值可表示：

I1=WrI

(28)

式中：Wr相对辐射功率值。衡量噪声大小时一般用声压级或声强级表示，声压级与声强级在数值上相等，由声强到声强级(或声压级)换算公式：

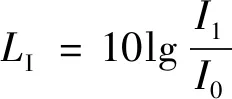
(29)

式中：I0为闻阈声压值，I0=1.0×10-12W·m-2。

由电磁振动噪声解析分析可知，引起电机振动噪声的根源为交变径向电磁力波，而极弧系数和磁极偏心距通过影响径向气隙磁密进而对径向电磁力波产生重要影响，最终影响电机电磁振动噪声的大小。因此,通过选取适当的极弧系数和磁极偏心距,降低径向电磁力波，能有效降低电机振动噪声。

本文以4.2 kW永磁电机为例，分析了如何选取磁极偏心距和极弧系数来使电机电磁振动噪声水平降到最小。由于该电机的极对数大于2，因此电机电磁振动噪声主要由主磁场与一阶磁导齿谐波作用产生的径向电磁力波激发产生。根据式(22)列出阶次小于等于4的力波阶数(本例中未出现小于4阶的分波分量)，如表2所示。

表2 主要力波阶次

选定极弧系数和磁极偏心距后，根据解析分析编写的计算程序，计算出各阶径向气隙磁密幅值并代入式(23)，求取表2中各主要电磁力波分量幅值，将所求每项力波分量幅值代入式(23)～式(29)对电机振动噪声进行计算，求取不同磁极偏心和极弧系数下电机振动加速度及噪声声压级，根据计算结果作出不同磁极偏心距下电机电磁振动加速度和噪声声强级随极弧系数的变化曲线。根据变化曲线研究极弧系数和磁极偏心距对电机电磁振动噪声的影响规律，具体流程如图4所示。

图4 振动速度及噪声声压级计算流程图

使磁极偏心距从0～18 mm变化，步长为3 mm，求取每一磁极偏心距下最大振动加速度分量的幅值随磁极弧系数的变化，计算结果如图5所示。从图5可以看出，当极弧系数不变时，随着磁极偏心距的增大，铁心表面振动加速度的最大分量幅值逐渐减小，减小幅度与极弧系数有关，在极弧系数为0.9附近减小幅度较小，在远离0.9处减小幅度较大。当磁极偏心距固定时，振动加速度最大值随着极弧系数的增大呈先减小后增大的趋势，每一磁极偏心距下最小值对应的极弧系数不同。

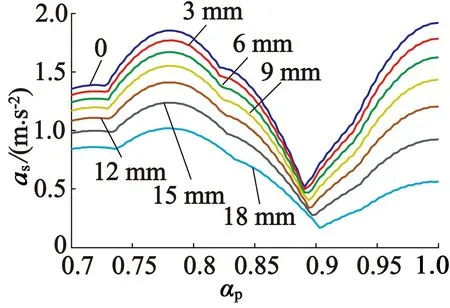
图5 不同磁极偏心距下最大加速度

同样，使磁极偏心距从0～18 mm变化，步长为3 mm，计算表2中每一力波所激发的电磁噪声声强值；然后，将各个分量叠加求取总噪声声强值，结果如图6所示。

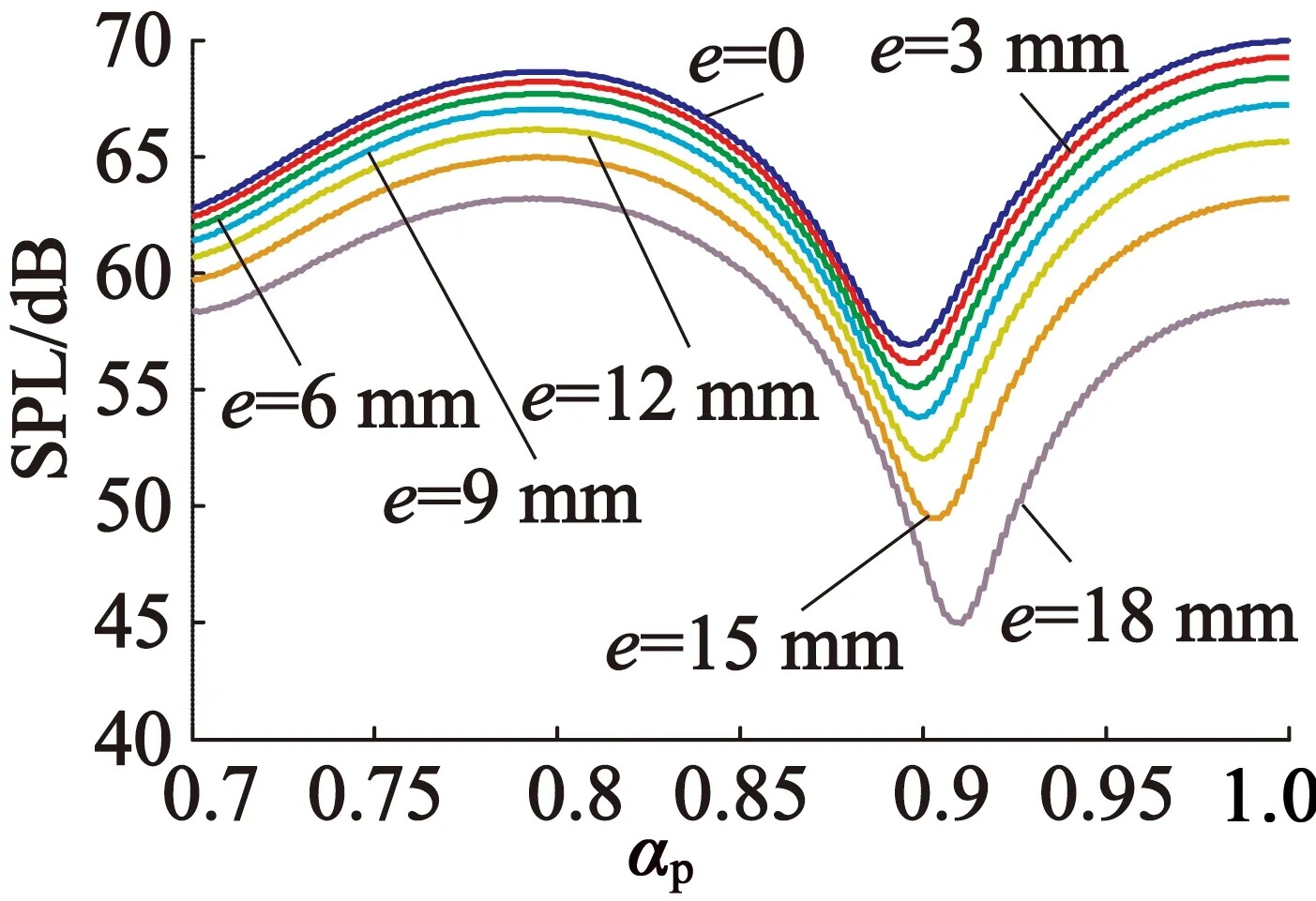
图6 不同磁极偏心距下噪声随极弧系数的变化

从图6可以看出，极弧系数不变时，随着磁极偏心距的不断增大，电机辐射的总噪声声强值逐渐变小。当磁极偏心距不变时，随着极弧系数的不断增大，电机辐射的总噪声强值出现先增大后减小的趋势，噪声会在极弧系数为0.9附近明显降低并达到最小。

因此，通过合理选择极弧系数和磁极偏心距的组合，可使电机电磁振动噪声水平降到最低。

4 有限元仿真验证

以表1所描述的电机为例，在Maxwell 2D中建立电机有限元仿真模型进行电磁场分析，求取径向气隙磁密及电磁力波，图7表示某一极弧系数及磁极偏心距下电机内部磁密分布。根据磁场计算结果，再对电机电磁振动噪声进行计算，得到不同磁极偏心距下电机电磁振动噪声值随极弧系数的变化曲线，如图8、图9所示。

图7 电机内部磁密分布

从图8可以看出，磁极偏心距小于18 mm时，当极弧系数不变时，随着磁极偏心距的逐渐增大，最大振动加速度分量幅值也不断增大。当磁极偏心距不变，极弧系数从0.7～1变化时，最大振动加速度分量幅值出现先减小后增大的趋势，在极弧系数为0.9～0.95之间出现极小值，并且每一磁极偏心距对应的极值点不同。上述变化规律与解析法计算结果相吻合。图9所反映的不同磁极偏心距下噪声声强级随极弧系数变化规律也与解析计算结果一致。

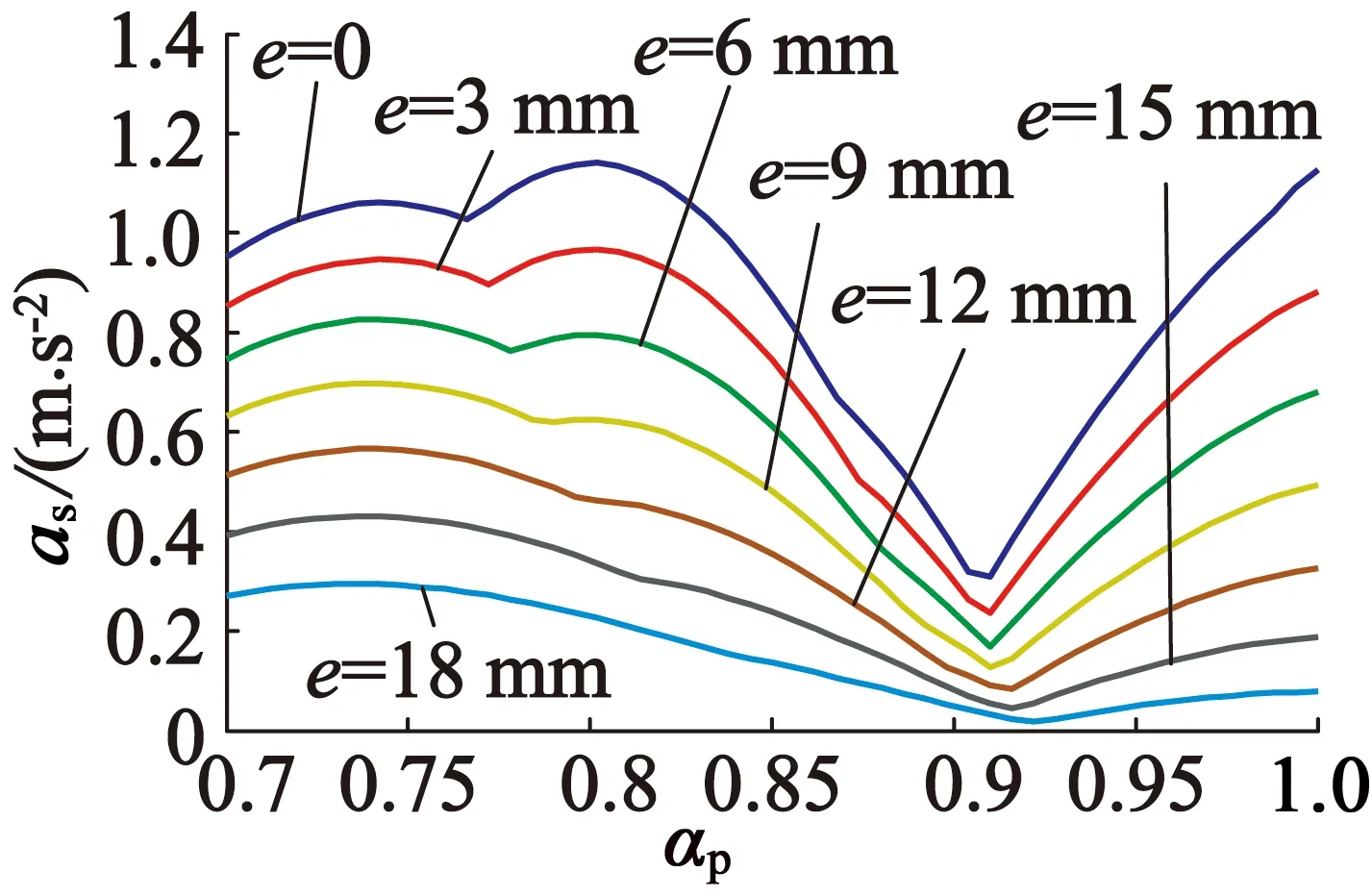
图8 不同偏心距下最大加速度幅值

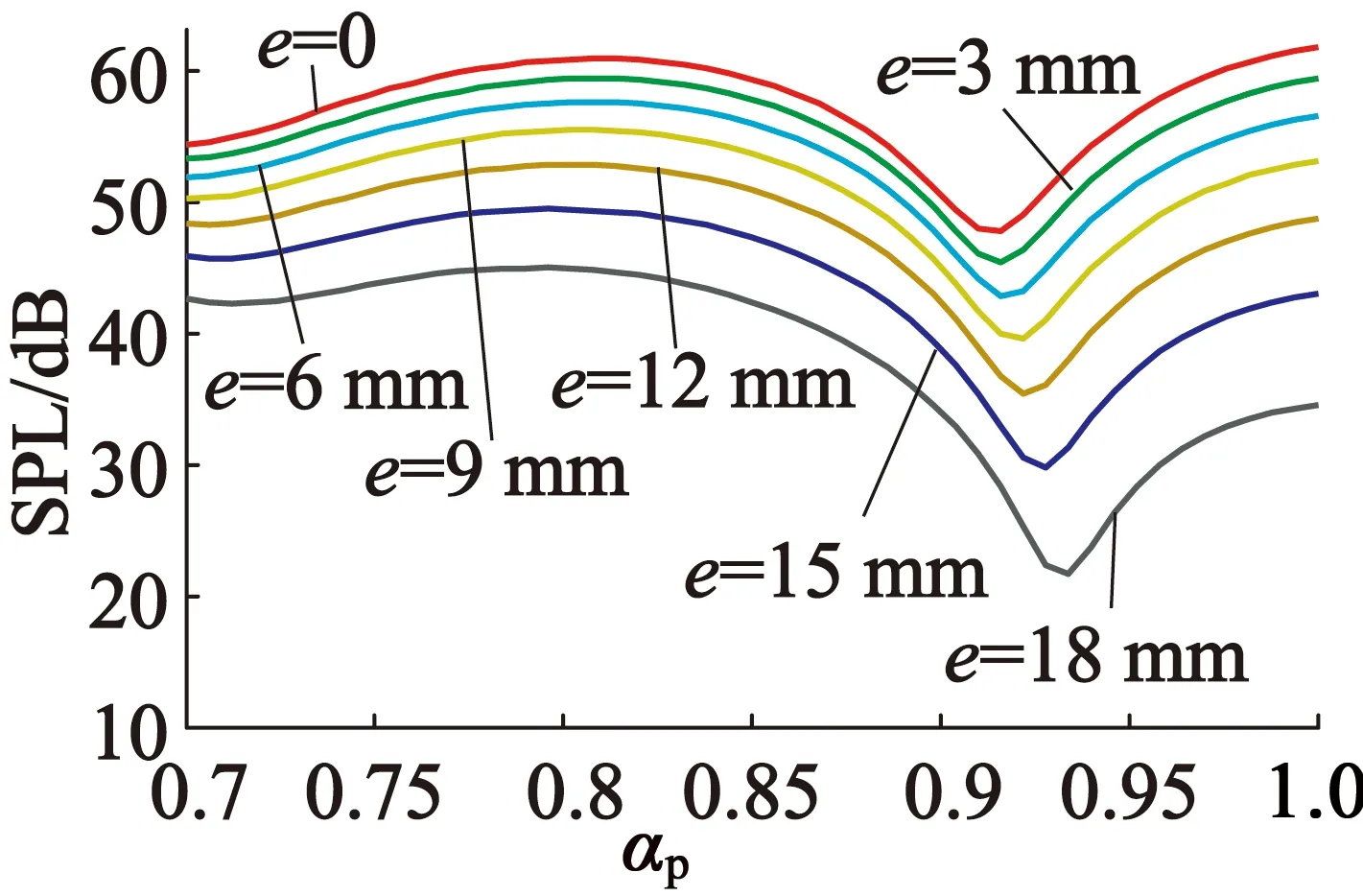
图9 不同磁极偏心距下噪声

由于解析法在计算过程中忽略了铁心磁压降等因素的影响，因此，解析法计算的振动加速度及噪声值明显偏大，每一磁极偏心距所对应的振动加速度及噪声值的极值点也略微有所差别，但两种计算结果所反映出的极弧系数和磁极偏心距对表贴式永磁同步电机电磁振动噪声影响的规律是相同的。

5 结 语

本文建立了径向磁密关于磁极偏心距和极弧系数的解析模型，分别利用解析法和有限元法对一台8极36槽电机振动噪声进行分析计算，得到磁极偏心距和极弧系数对电机振动噪声的影响规律。结论如下：

1)电机其他条件不变，当极弧系数一定时，随着磁极偏心距的增加，表贴式永磁电机电磁振动噪声逐渐降低。

2)当磁极偏心距一定时，极弧系数在一定取值范围内电机电磁振动噪声随极弧系数的增大而基本呈现先增大后减小的变化趋势。

3)在低振动噪声电机设计时，极弧系数是很重要的设计参数。对于8极36槽表贴式永磁电机，当极弧系数为0.9附近时，电机振动噪声会降到最低值。