永磁同步电机转子结构优化设计
诸德宏,简 耀,李明达
(江苏大学,镇江 212013)
0 引 言
内置式永磁同步电机被广泛应用在电动汽车、混合动力汽车以及很多其他工业设备中[1-4]。然而,由于电机结构的凹凸性及磁场耦合效应的影响,内置式永磁同步电机具有较大的转矩脉动,这在很多场合会带来不利的影响。因此,降低内置式永磁同步电机的转矩脉动非常重要。影响转矩脉动的因素主要分控制方面和本体方面。控制方面受导通压降,死区时间,电流采样精度等影响;本体方面主要受齿槽转矩,反电动势波形畸变,磁路饱和等影响。
目前,国内外学者对降低转矩脉动的方法进行了大量研究,一部分学者从控制角度研究[5-6],但更多的是从本体角度研究如何减小转矩脉动。定子斜槽、转子斜极的方法有利于减小齿槽转矩[7],但这种方法使电机成本增加;转子铁心开辅助槽[8]、优化定子槽开口宽度等能有效降低齿槽转矩,但这些方法并不一定能有效降低转矩脉动。优化永磁体形状是一种有效降低转矩脉动的方法,比如重新设计永磁体形状,改变永磁体尺寸等。文献[9]通过分析一个定转子之间谐波相互作用的解析表达式,给出了一种降低转矩脉动的方法,即每对磁极对应奇数个定子槽的方法。
本文从降低内置式永磁同步电机齿槽转矩、减小反电动势波形畸变的角度出发,通过改变永磁体形状和转子铁心外表面形状来减小齿槽转矩和反电动势谐波含量,从而降低转矩脉动。本文首先介绍了优化后的转子拓扑结构,然后详细介绍了该结构的设计原理,用Maxwell 2D软件对电磁特性进行计算分析,最后采用Taguchi法(田口法)来确定参数的最佳取值组合,并与传统“一”形转子结构电机性能对比,结果表明该优化方法有效。
1 拓扑结构
本文选择一种常见的3相4极24槽的内置式永磁同步电机为分析模型,电机优化模型的横截面图如图1所示。图2~图4分别给出折线形永磁体、转子铁心分段圆弧结构和角形槽的结构示意图。从图1中可以看出,这种转子结构具有以下特点:永磁体为三段折线形,两端开有空气隔磁槽,相邻段的永磁体夹角为α;转子铁心外表面由直轴侧圆弧和交轴侧圆弧平滑连接组成,且两类圆弧不同心;转子表面开有角形槽。
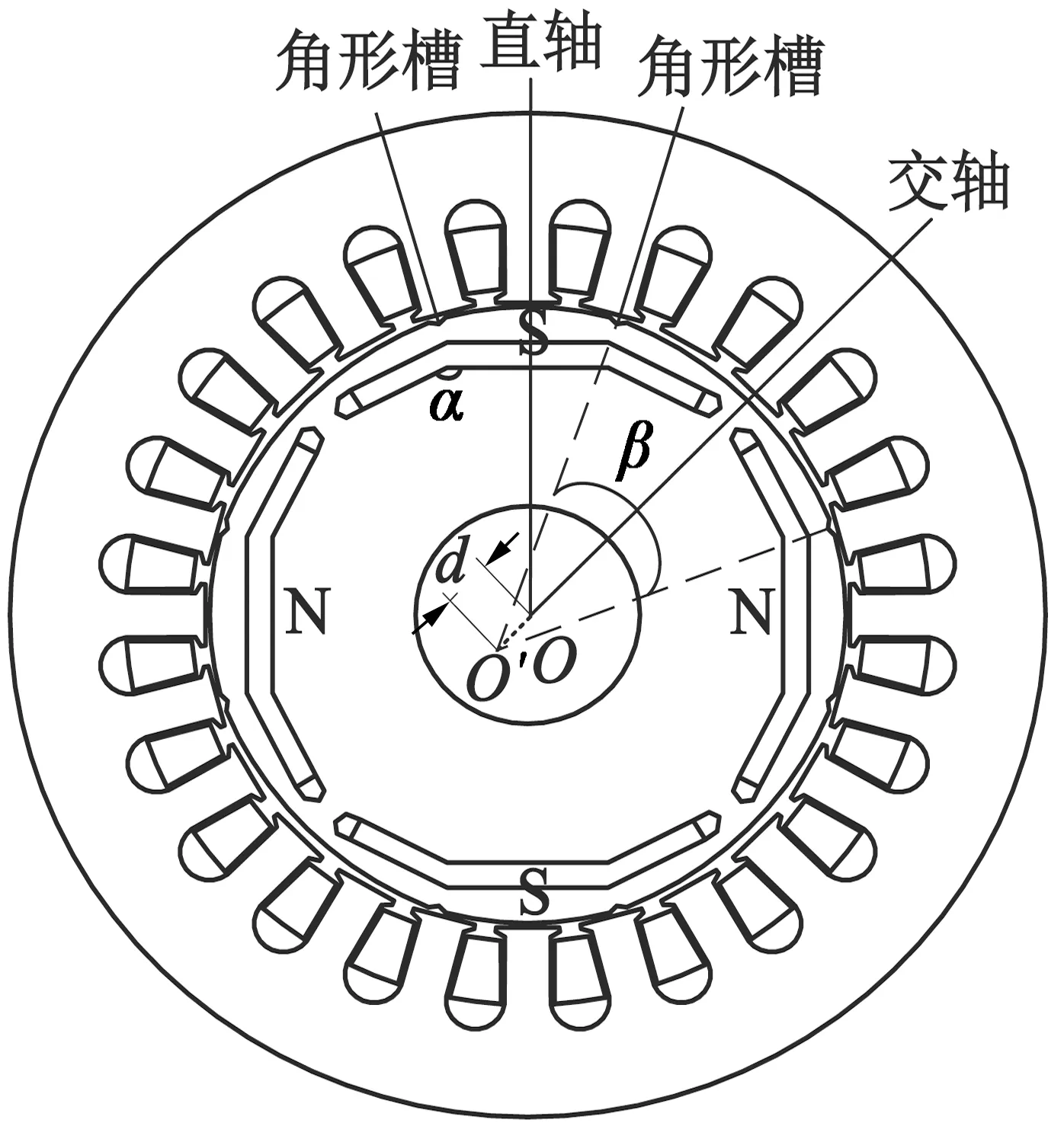
图1 电机优化模型横截面图
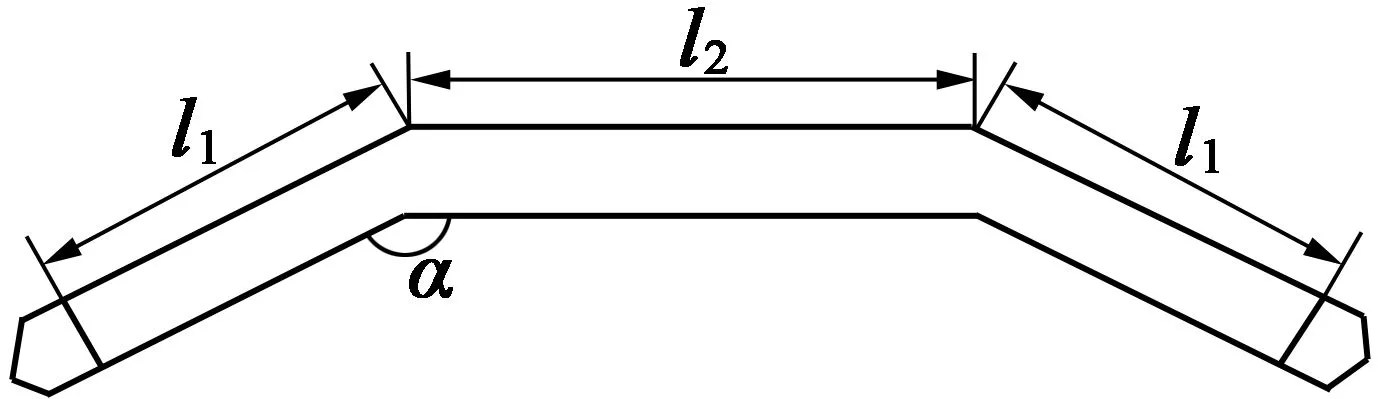
图2 折线形永磁体结构示意图
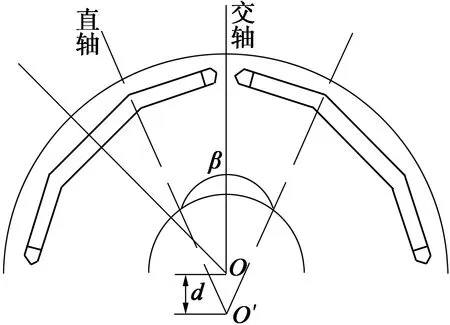
图3 转子铁心分段圆弧结构示意图
如图2所示,折线形永磁体相邻段的夹角α和相邻段的长度比值都会影响气隙磁场的分布,本模型取l1∶l2∶l1=2∶3∶2;α取150°。不同于传统不均匀气隙的转子铁心结构,本文提出了一种外表面采用分段圆弧的铁心结构,如图3所示。转子铁心外表面直轴侧圆弧与定子内圆同心,圆心为O;交轴侧圆弧以O′为圆心,圆心角为β,偏心距为d。
为减小齿槽转矩,在直轴侧圆弧与交轴侧圆弧相交处,开角形槽,如图4所示,采用辅助同心圆来确定角形槽的形状及尺寸。确定方法如下:以直轴侧圆弧、交轴侧圆弧连接点D为圆心作同心圆,外圆半径为R,内圆半径为r,如图5所示。外圆与直轴侧圆弧交点记为A,与交轴侧圆弧交点记为C,过D和O′的直线交内圆于B。A,B,C即为角形槽的三个顶点,由此可以确定角形槽的形状。改变R,r值,即可改变角形槽的开口角度及深度。
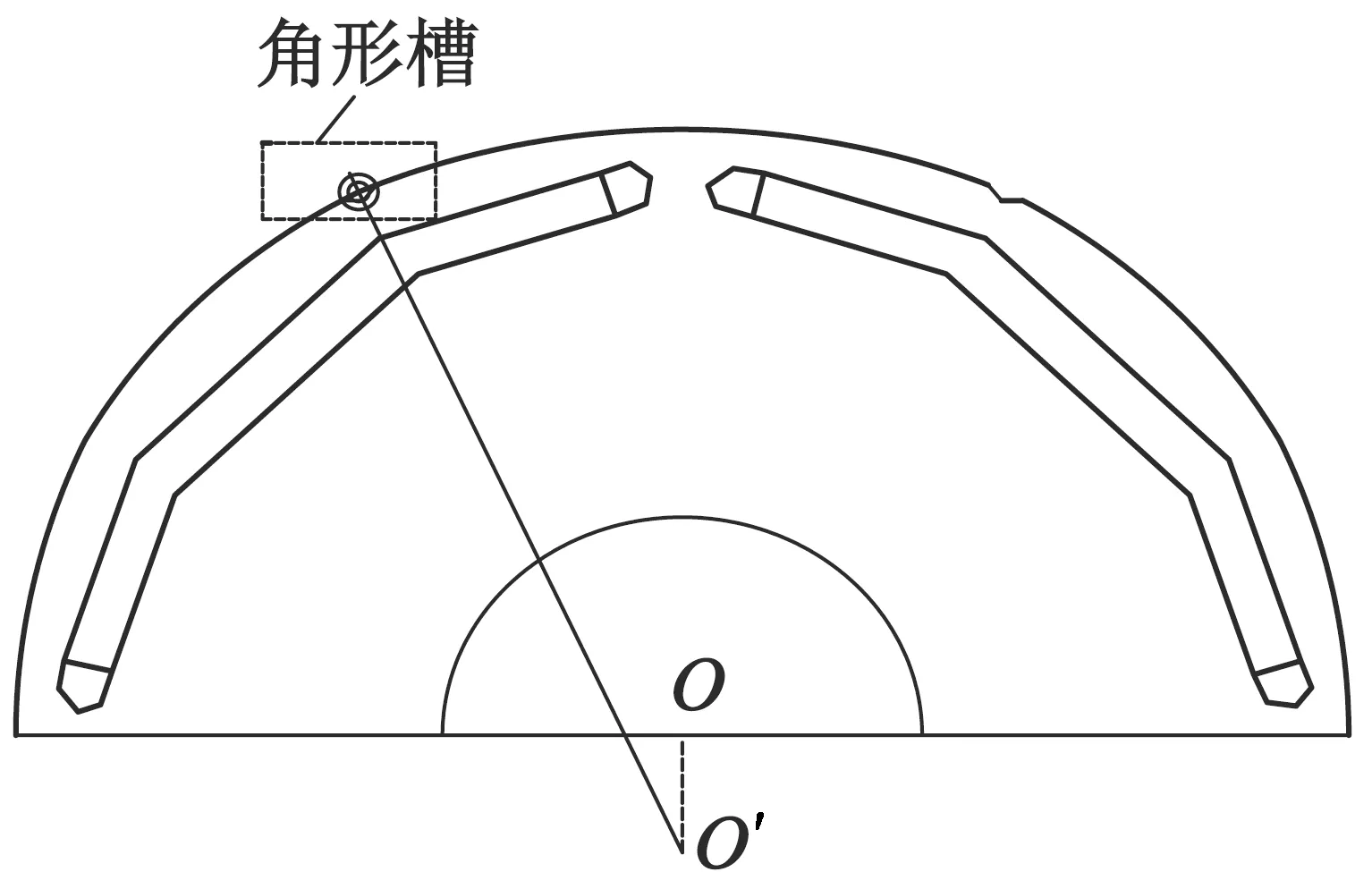
图4 角形槽位置图
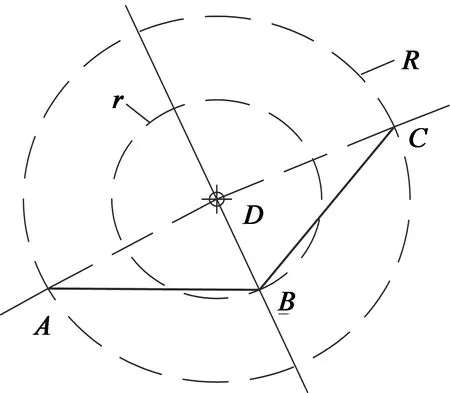
图5 角形槽结构放大图
2 磁场及齿槽转矩分析
2.1 气隙磁场分析
利用解析法分析内置式永磁同步电机气隙磁密,可以找到影响气隙磁密的具体结构参数[10]。假设铁磁材料的磁导率为无穷大,并忽略电动机漏磁,在定子不开槽时,永磁体产生的气隙磁密幅值Bδ:
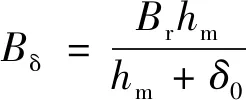
(1)
永磁体产生的气隙磁密:
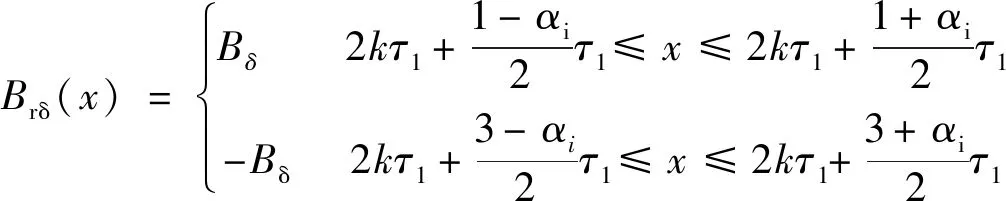
(2)
式中:Br为永磁体剩磁;hm为永磁体磁化方向长度;δ0为气隙长度;τ1为齿距电角度。定子开槽后,考虑漏磁及磁路饱和的影响,气隙磁密傅里叶分解表达式[10]:
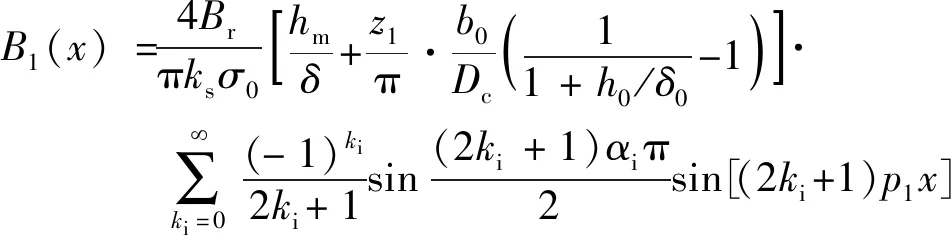
(3)
式中:b0,h0,δ0,αi,ks,σ0分别为定子槽口宽、定子槽深、等效气隙长度、极弧系数、饱和系数、漏磁系数;B1(x)是永磁体产生磁动势与气隙平均磁导引起的气隙磁密;B2(x)是永磁体产生的磁动势与定子齿谐波引起的气隙磁密。
由以上推导可知,等效气隙长度δ0是影响气隙磁场波形的因素之一,合理设计等效气隙长度可以优化气隙谐波含量。
2.2 齿槽转矩分析
相对于均匀气隙的转子铁心,分段圆弧形转子铁心结构直轴侧气隙长度不变,交轴侧气隙长度略变大,这样设计可以减小对气隙磁路的消极影响。同时,交轴侧圆弧与直轴侧圆弧在连接点处气隙长度与直轴侧气隙长度相等(即均匀气隙磁场的长度),因此在连接点处磁场分布可按照均匀气隙情况分析。齿槽转矩定义为电机不通电时的磁场能量W对定转子相对位置角α的负导数[11],即:
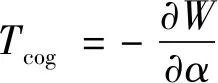
(5)
为了便于分析,作出如下假设[12]:电枢铁心的磁导率无穷大;永磁体的磁导率近似与空气相同;铁心叠压系数为1,规定α为定转子之间的相对位置角,θ=0的位置在永磁体的中心线上。电机内存储的能量近似为电机气隙和永磁体中存储的磁场能量之和,即:
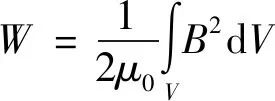
(6)
气隙磁密沿电枢表面分布可近似表示:
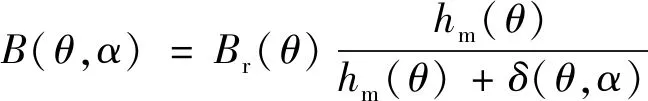
(7)
式中:Br(θ),δ(θ),hm(θ)分别为永磁体剩磁、有效气隙长度、永磁体充磁方向长度。将式(7)代入式(6):
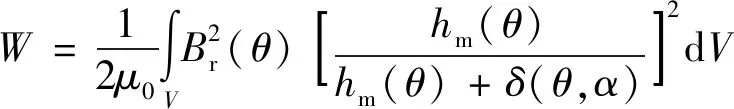
(8)
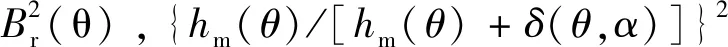
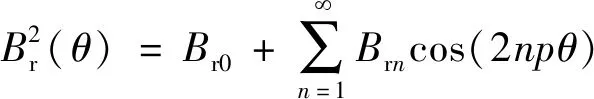
(9)
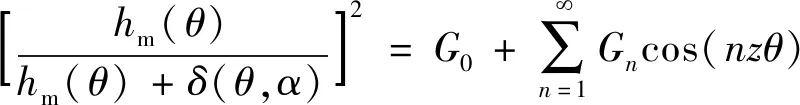
(10)
综合式(5)、式(8)~式(10),可得齿槽转矩解析表达式:
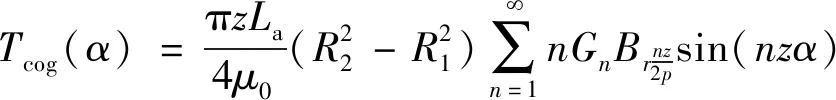
(11)
式中:La为铁心轴向长度;R1,R2为转子外径和定子内径;n为使nz/(2p)为整数的整数,z为槽数与极数的最小公倍数。
内置式永磁电机在转子外表面开辅助槽,增大了有效气隙长度,根据式(11),转子表面开尺寸合适的槽,可以减小Brn,从而减小齿槽转矩[13],磁力线分布如图6所示。
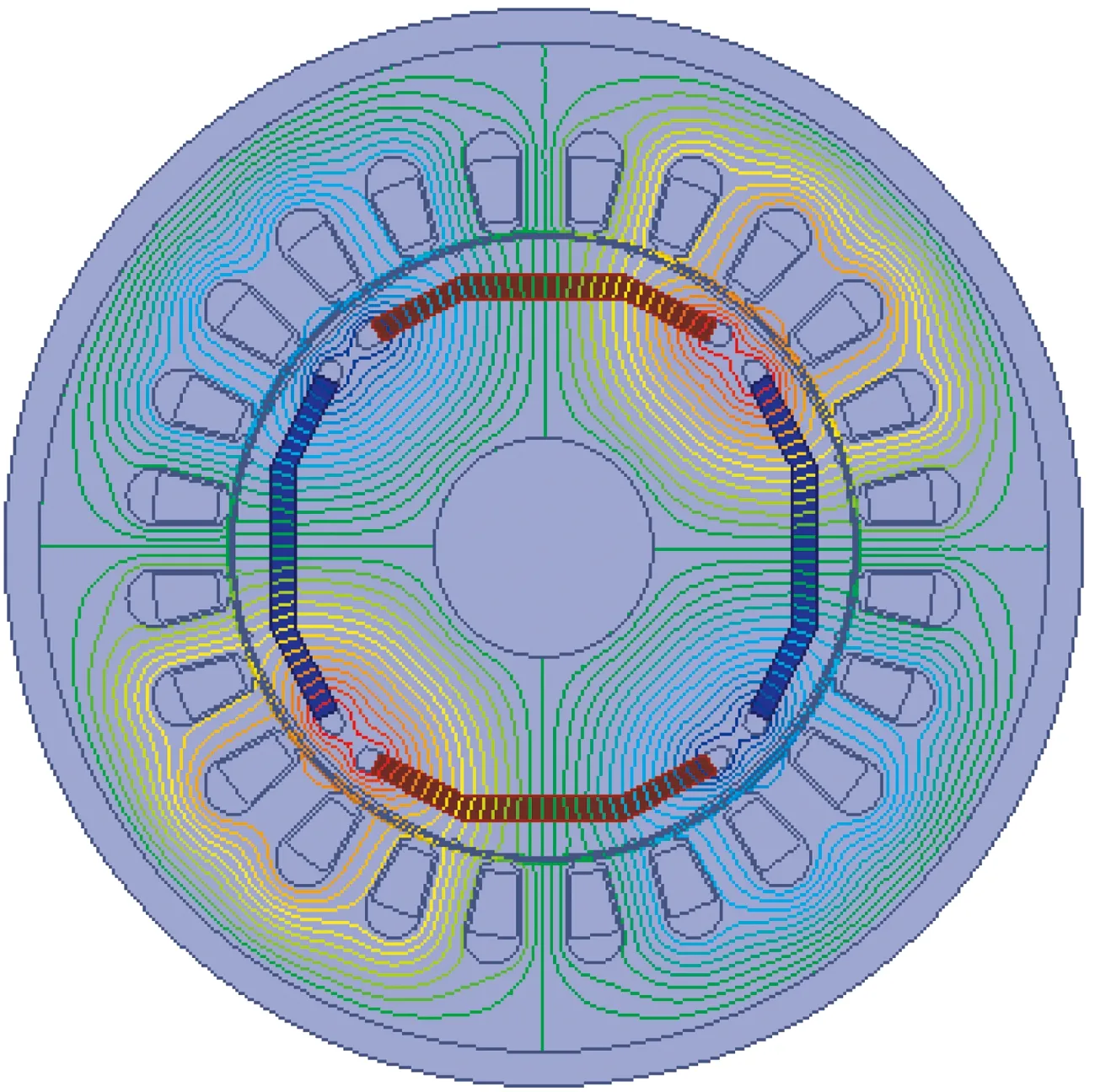
图6 磁力线分布图
3 有限元仿真
3.1 参数化分析
当β不变时,对d进行参数化分析,所对应的空载反电动势谐波分布情况如图7所示;当d不变时,对β进行参数化分析,所对应的空载反电动势谐波分布情况如图8所示。本文初始模型d取6 mm,β取47°,最佳取值的确定方法将在下文Taguchi法参数优化部分给出。

图7 d参数化对应的反电动势谐波分布

图8 β参数化对应的反电动势谐波分布
从图7、图8可以看出,反电动势各次谐波幅值会随着d,β的变化而变化,说明d,β的取值会影响气隙磁场谐波的分布情况。
当r不变时,R参数化对应的齿槽转矩分布如图9所示;当R不变时,r参数化对应的齿槽转矩分布如图10所示。本文初始模型R取1.06 mm,r取0.53 mm,最佳取值同样在下面Taguchi法优化部分给出。
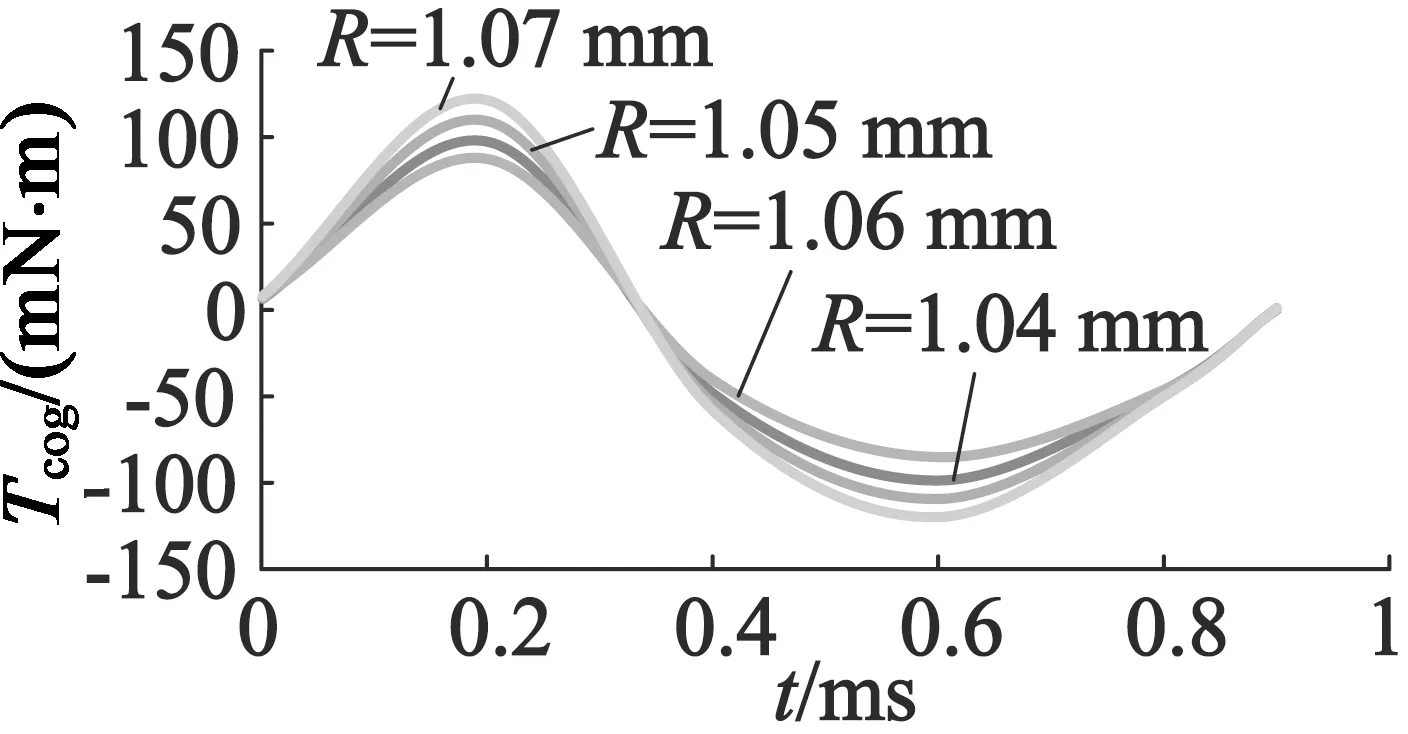
图9 R参数化对应的齿槽转矩分布
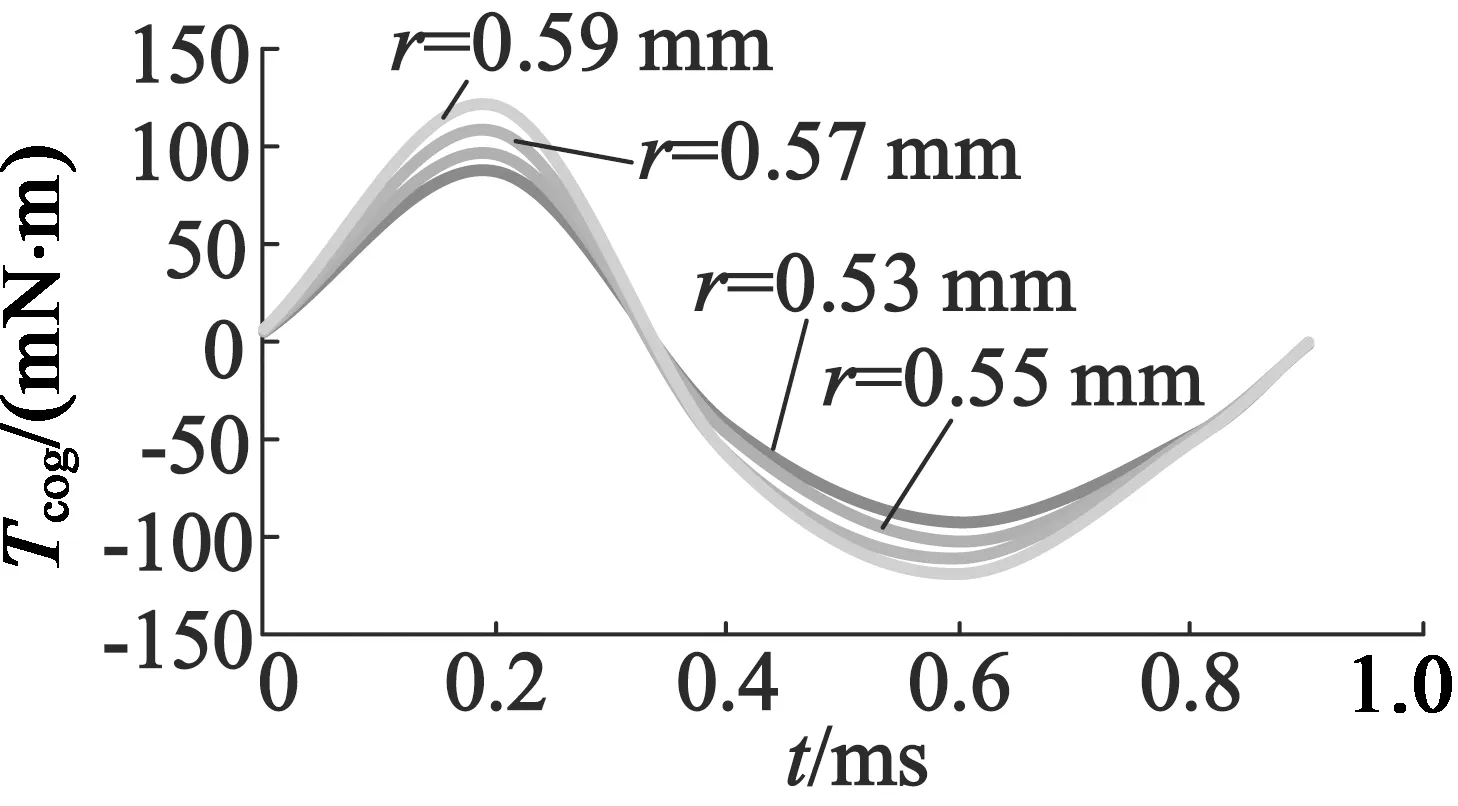
图10 r参数化对应的齿槽转矩分布
从图9、图10可以看出,齿槽转矩幅值会随着R,r的改变而改变,说明槽的宽度及深度会影响齿槽转矩的大小。
3.2 电机特性分析
图11是传统“一”形永磁体的内置式永磁同步电机和三段折线形永磁体内置式永磁同步电机空载反电动势谐波对比图。在本次仿真中,两种电机模型转子铁心均采用传统的均匀铁心,除永磁体外,两个模型的尺寸、参数取值全部相同。图12是两个模型齿槽转矩的对比图。

图11 反电动势谐波对比

图12 齿槽转矩分布对比
从图11可以看出,折线形永磁体的电机基波幅值远大于“一”形永磁体结构电机,这是因为折线形永磁体的永磁材料用量比“一”形永磁体略多;3次,5次,7次谐波要比“一”形磁钢电机低,其余次谐波相差不大。谐波含量计算公式[14]如下:

(12)
由于空载反电动势只含有奇数次谐波,所以n的取值为除1之外的奇数;因为定子绕组采用Y形连接,所以3次及3的倍数次谐波可以相互抵消,故n的取值不包含3及3的倍数。
根据式(12),折线形永磁体的永磁电机反电动势谐波含量明显低于“一”形磁钢永磁电机;从图12可以看出,齿槽转矩幅值相差不大。因此,采用三段折线形磁钢的永磁电机有利于降低磁场谐波含量和空载反电动势波形畸变率。
传统均匀铁心转子结构的永磁电机与本文的带有角形槽的分段圆弧转子铁心永磁电机性能的对比如图13、图14所示。两种模型都采用三段折线形永磁体,除转子铁心外表面结构外,其余尺寸、参数完全相同。
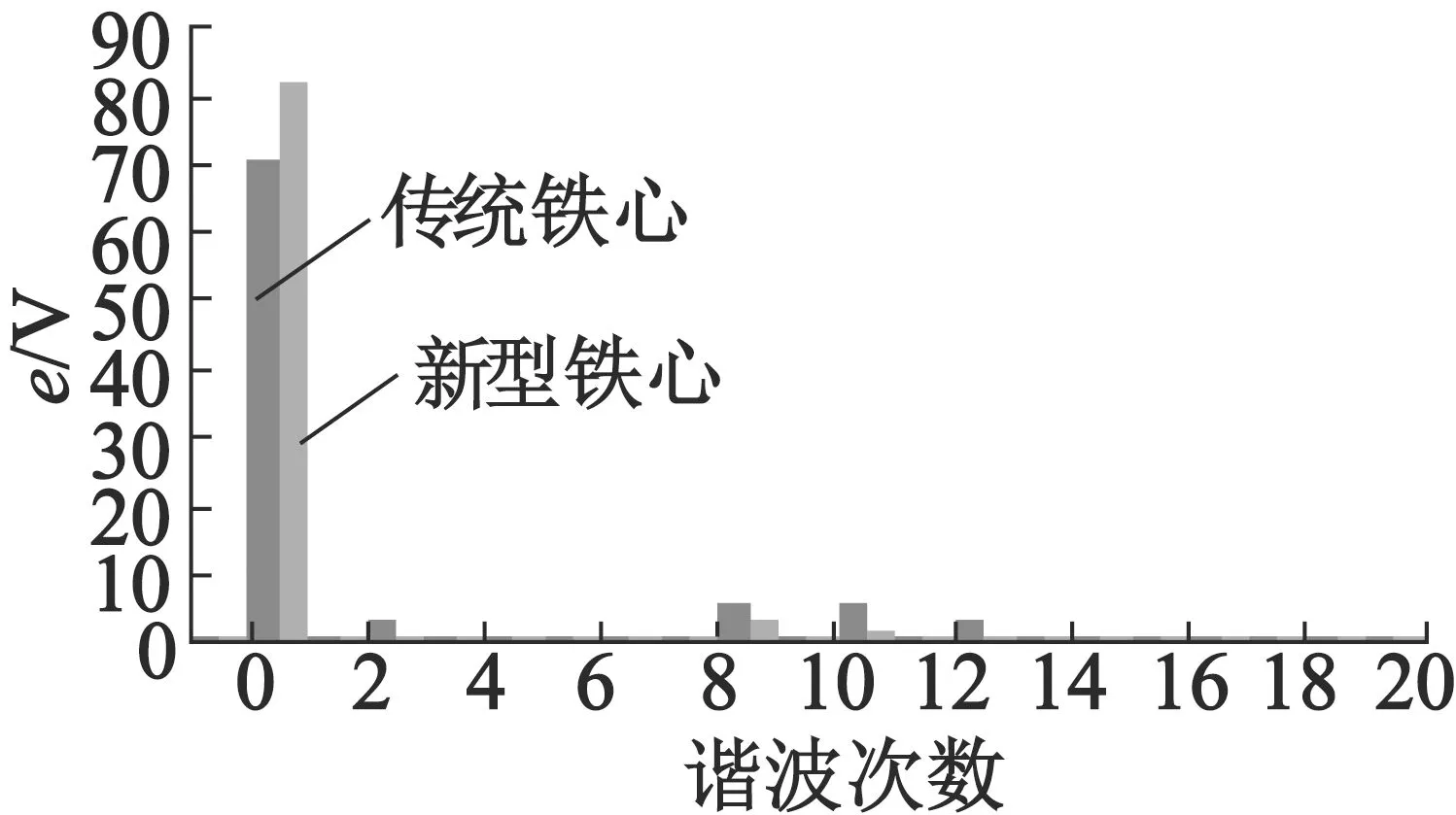
图13 不同铁心结构反电动势谐波对比

图14 不同铁心结构齿槽转矩对比
从图13中可以看出,新型转子铁心永磁电机反电动势的基波幅值大于传统铁心永磁电机基波幅值;同时,其高次谐波幅值要明显低于传统铁心永磁电机谐波幅值。从图14中可以看出,新型铁心永磁电机齿槽转矩平均幅值明显比传统铁心永磁电机齿槽转矩平均幅值降低了约25%,其齿槽转矩的周期数略多于传统铁心结构的永磁电机。
4 Taguchi法参数优化
从上文对d,β,R,r的参数化分析中可以看出,d,β,R,r是设计分段圆弧和角形槽的关键参数,它们的取值会对优化效果产生较大影响,但是不能简单地取各自参数化后的最优值作为最终设计的参数取值。参数化过程始终保持着某一个参数不变,而这个参数取不同值必会导致其他参数化最优值不同,因此,需要一种将这4个参数统筹起来找到最佳组合的方法。本文采用Taguchi法对4个参数进行协同优化,最后确定最佳的参数组合。
表1给出了每个因子所对应的3个水平,表2给出了L9(34)正交表,表3给出的是9次正交试验的结果,其中Tc,THD,Ta分别是齿槽转矩峰峰值、谐波含量、额定工况下输出转矩平均值。
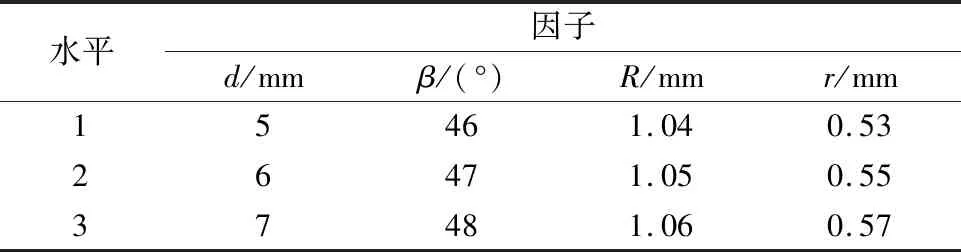
表1 设计变量及影响因子水平取值
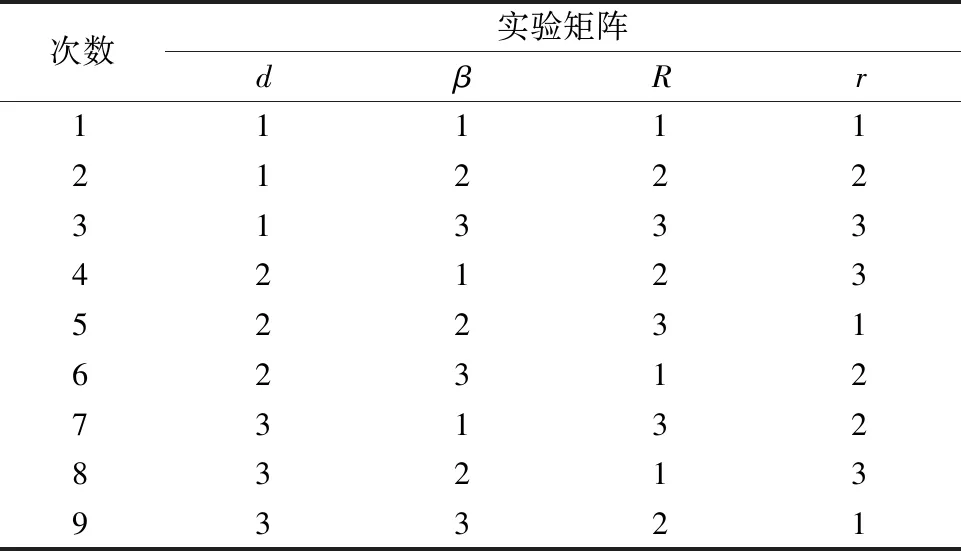
表2 L9(34)正交表
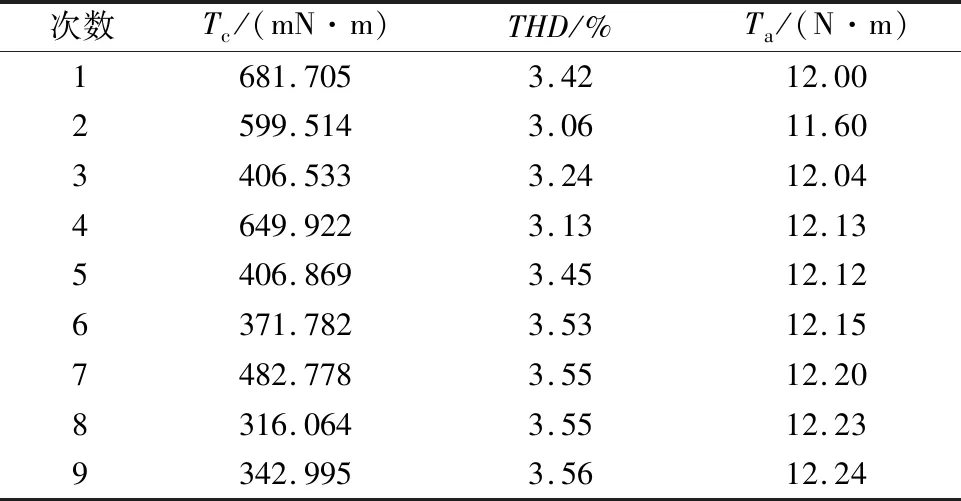
表3 正交试验的结果
由表3可以计算出,9次试验的齿槽转矩峰峰值平均值为473.13 mN·m,9次试验谐波含量THD的平均值为3.39%,9次试验输出转矩的平均值为12.08 N·m。
每个参数改变时对应某一性能指标下的计算结果的平均值[11]计算方法如下,例如因子A在水平2下,其品质T的所有计算值为T1,T2,T3,则计算公式[15]:
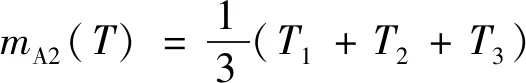
(13)
平均值计算结果如表4所示。

表4 一种试验条件下因子变化的平均值
各变量对电机特性影响的相对重要性计算公式:
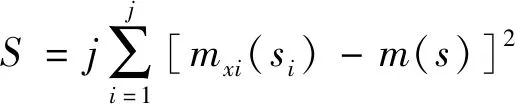
(14)
式中:S表示各变量对电机特性影响的相对重要性;mxi(si)表示一种试验条件下因子变化的平均值,其值如表4所示;m(s)为根据表3计算出来的平均值。相对重要性的计算结果如表5所示。
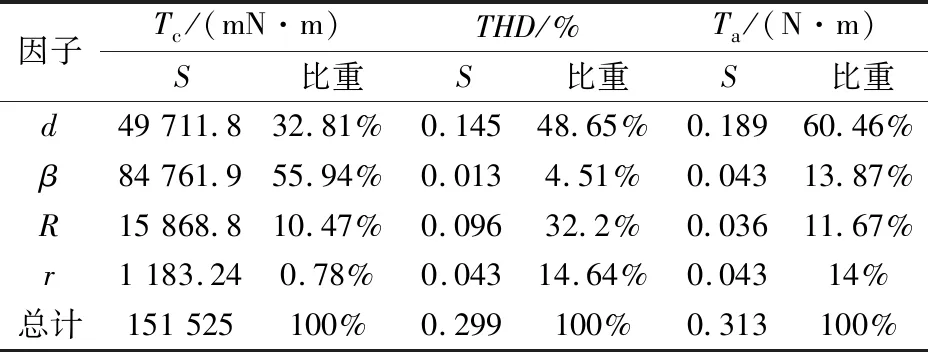
表5 各变量对电机特性影响的相对重要性
综上分析,d对Ta的影响最大,d的选择应该以使Ta最大为原则;β对Tc的影响最大,在选择时应该以使Tc最小为原则;R对THD的影响最大,在选择时应该以使THD最小为原则,r对THD的影响最大,在选择时以THD最小为原则。由表4可以得出:d应取水平3;β应取水平3;R应取水平2;r应取水平3。
按照Taguchi法计算出的参数最佳组合建立模型,对其进行有限元仿真,结果如图15、图16所示。
从图15中看出,优化后的齿槽转矩幅值低于优化之前。从图16可以看出,空载反电动势基波幅值变化不大,但3次,7次,9次,11次谐波较优化之前都有所减小,说明用Taguchi法选择参数值是有效的。
两种转子结构的永磁同步电机额定工况下输出转矩对比如图17所示,一种采用传统转子结构,永磁体为“一”形,另一种采用本文新型转子结构,永磁体为折线形。
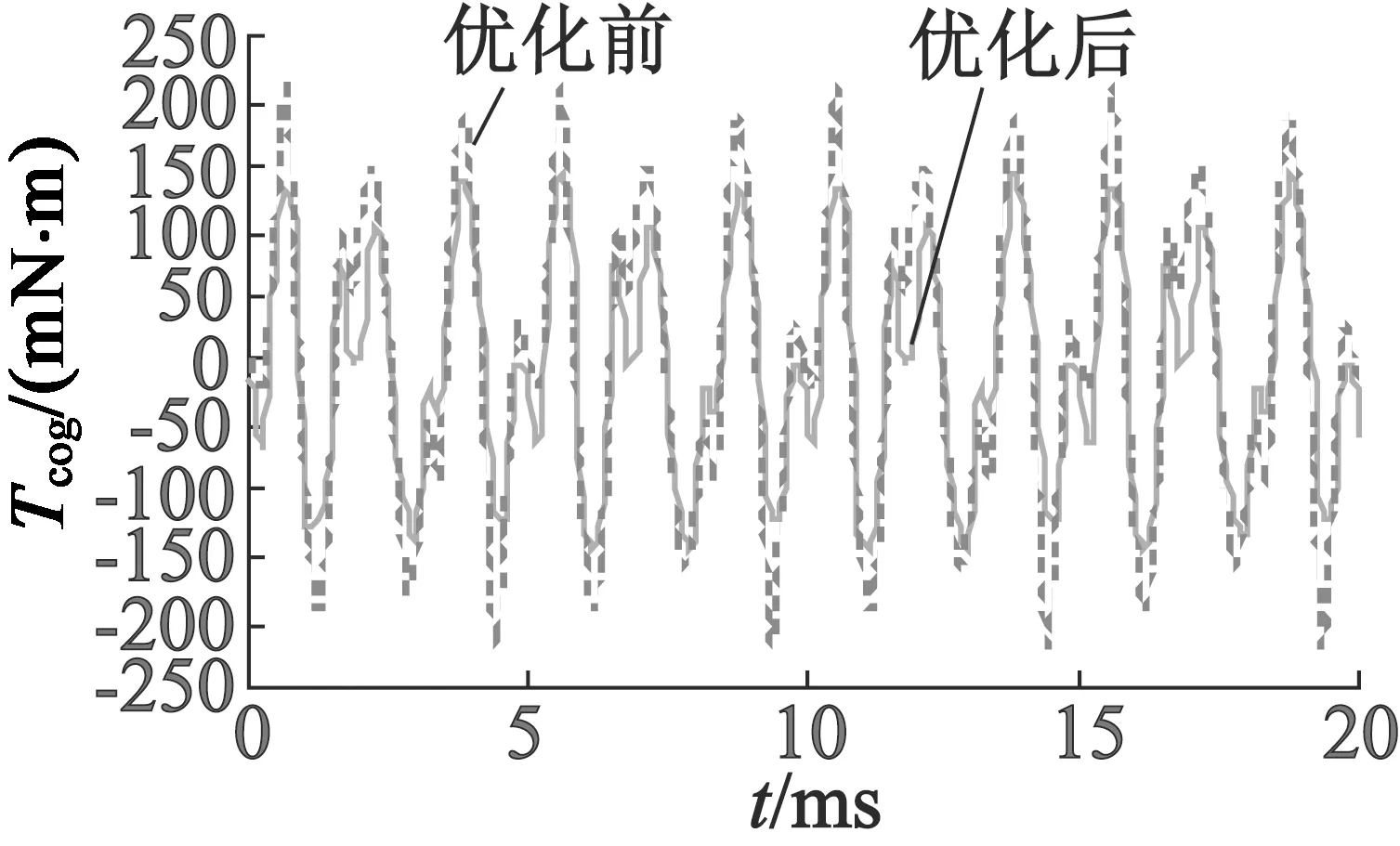
图15 参数优化前后齿槽转矩对比

图16 空载反电动势谐波分布对比
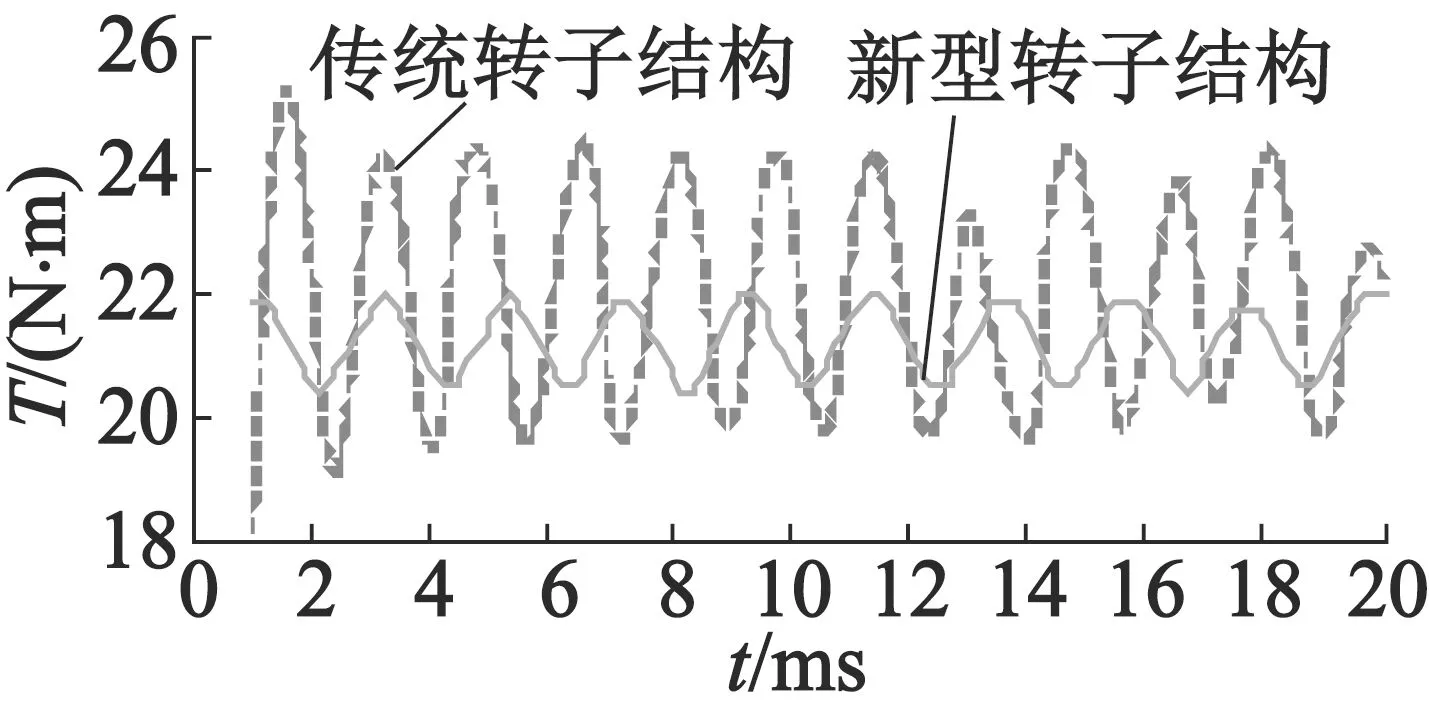
图17 输出转矩对比图
从图17中不难看出,采用新型转子结构的永磁电机,其输出转矩脉动明显较小,该结果说明新型永磁同步电机转子结构可以有效降低转矩脉动。
5 结 语
本文研究了一种降低转矩脉动的内置式永磁同步电机转子优化结构,使用Maxwell2D对其特性进行有限元分析,并通过Taguchi法选择重要参数的最佳取值组合,通过与传统“一”形永磁体结构永磁同步电机的对比,得出如下结论:
1) 采用新型转子结构的内置式永磁同步电机相比传统转子结构的永磁同步电机,可以明显减小齿槽转矩,降低气隙磁场和空载反电动势中的谐波成分。
2) 采用新型转子结构的内置式永磁同步电机可以有效降低输出转矩脉动。

