2种时间尺度下稻田蒸散模型比较

李谦 景元书 李轲

摘要：准确估算稻田蒸散量，对于提高稻田灌溉管理精度和水资源利用效率具有重要意义。根据波文比系统与自动气象站实测数据，利用FAO-Penman-Monteith、FAO-17-Penman以及Priestley-Taylor模型对稻田蒸散量进行模拟，探究2种时间尺度上蒸散模型對蒸散量的估算精度差别。结果表明，各模型估算值与波文比计算值的整体变化趋势一致，但逐时、逐日尺度上各模型估算蒸散值与实测值的拟合效率差别明显。逐时尺度上，Priestley-Taylor模型的拟合效率较高，FAO-PM模型次之，FAO-17-Penman模型的最差。但在逐日尺度上，FAO-PM模型和Priestley-Taylor模型的拟合效率均较高，FAO-17-Penman模型的最差。研究结果对于局地地区在不同时间尺度上选取合适蒸散模型具有一定的指导意义。

关键词：稻田;逐时;逐日;蒸散模型

中图分类号：S161.4   文献标志码： A  文章编号：1002-1302（2019）05-0238-06

收稿日期：2016-07-13

基金项目：国家自然科学基金（编号：41575111、41175098）;江苏省第九批“六大人才高峰”高层次人才项目（编号：NY-038）。

作者简介：李 谦（1993—），女，江苏淮安人，硕士研究生，主要从事农业气象、应用气象研究。E-mail：dzng1993@sina.com。

通信作者：景元书，博士，教授，主要研究方向为农业气象与生态环境。E-mail：jingyshu@163.com。

蒸散是SPAC（Soil-Plant-Atmosphere Continuum）系统中水分运动的重要过程[1]。准确估算稻田蒸散量、提高用水效率，对于解决我国不同地区的水资源短缺与采取相应措施精准管理稻田用水至关重要[2]。

20世纪以来，国内外蒸散量的传统测定方法主要分为微气象方法（空气动力学法、波文比-能量平衡法、涡度相关法等）、水文学方法（蒸渗仪法、水量平衡法等[3]）和植物生理学方法（同位素示踪法、热计数法等）这三大类。随着遥感技术的产生与发展，遥感技术开始应用于作物蒸散方面，并为大尺度作物蒸散量的研究开辟了新的道路[4-6]。这些方法所需参数不同，原理各异，在实际应用中都有一定的优势与局限性。其中，波文比-能量平衡法与其他方法相比具有价格便宜、简便易行等优点，在实际应用中可通过改进仪器设备和计算方法将误差降低到10%以下[7]。与此同时，国内外专家与学者也提出了一系列的经验模型。比较具有代表性的有：Penman-Monteith模型、Priestley-Taylor模型、Hargreaves模型、Shuttleworth-Wallace模型、SWAT模型[8]等。

纵观作物蒸散研究的发展历程，传统方法往往侧重于孤立的单一时间尺度，但对于时间尺度转换方法和模型在不同时间尺度应用方面，依然缺乏足够的研究。1983年，Jackson在假设蒸散日际变化与太阳辐照度变化相似的基础上，建立了尺度转化模型[9]。2008年，杨汉波通过水热耦合平衡方程，模拟出了我国位山实验站和俄罗斯西伯利亚Yakutsk实验站中月、旬和日时间尺度上的实际腾发量[10]。2011年，杨秀芹针对南四湖流域FAO Penman-Monteith模型的适用性研究认为，在日、月不同时间尺度上，FAO PM模型的结果值相关性显著[11]。2014年，魏新光在对旱区枣林的蒸腾及其影响因子的关系进行分析研究时发现，蒸散影响因子具有明显的时间变异性和时间尺度效应[12]。尽管近些年的研究方向已初步向时间尺度倾斜，但大多局限于单一模型的升降尺度分析和多种模型相同时间尺度的对比分析，对于不同蒸散模型之间的时间尺度对比却始终没有给予足够的关注。

因此，本研究在田间波文比系统与自动气象站实测数据的基础上，利用FAO-Penman-Monteith、FAO-17-Penman以及Priestley-Taylor模型进行计算与模拟，分析比较逐时、逐日时间尺度上各模型的可靠性，以便在不同时间尺度上选取合适蒸散模型，提高蒸散量估算精度和实际应用的合理性。

1 材料与方法

1.1 试验设计

试验区位于江西省鹰潭市中国科学院红壤生态实验站附近（116°55′E，28°15′N），属于亚热带湿润季风气候。年均降水量1 788.8 mm，年均水面蒸发量1 229.1 mm。年无霜期258 d。试验对象选取晚稻，于2014年6月17日播种，7月10日移栽，11月5日收获。水稻移栽后各类田间管理等同当地大田生产，成熟后期因水稻收割停止灌溉，分析时不予考虑。试验期间的各类气象要素情况见表1。

试验田区布设自动气象站和稻田换位式波文比测量系统。自动气象站仪器型号为美国ONSET公司所产HOBO U30，每30 min对气温、降水量、2 m风速、相对湿度、气压等小气候数据进行观测记录1次。波文比系统由双层空气温湿度传感器（HMP155A）、风速仪（010C-1）、净辐射传感器（NR-Lite）、CR1000数据采集器等组成。每20 min自动采集2 m高度差之间的温湿度梯度1次，由此直接计算、存储波文比并求得蒸散值。

1.2 模型介绍

式中：ET0为作物潜在蒸散（mm/d）;Δ为水汽压曲线斜率;Rn为净辐射[MJ/（m2·d）];G为土壤热通量[MJ/（m2·d）];γ为干湿表方程常数（kPa/℃）;T为距地面2米处空气温度（℃）;U2为距地面2米处风速（m/s）;es为空气温度T下的饱和水汽压（KPa）;ea为空气温度T下的实际水汽压（kPa）。

式中：ET0（FAO-17-PM）为计算得到的日参考作物蒸散量（mm/d）;P0为海平面大气（hPa）;P为本站气压（hPa）;Δ、γ物理意义同公式（1），单位改变为hPa/℃;Rn物理意义同公式（1），单位改变为mm/d。

式中：常数α为无量纲经验修正项，变化范围为1.2～1.3。本研究计算代入值为1.26，即湿润气候条件时α常数值。且Rn为净辐射通量密度（W/m2），G为土壤热通量密度（W/m2）。

1.3 数据预处理

波文比仪数据处理时，剔除极个别由于仪器故障或极端天气引发的异常值。采取线性插值法对2 h内缺失数据进行补充。2 h以外缺失的数据，根据环境因子，建立相关关系进行补充，并采用线性回归分析模拟值与观测值的相关性。

2 模型结果对比

2.1 FAO-Penman-Monteith模型

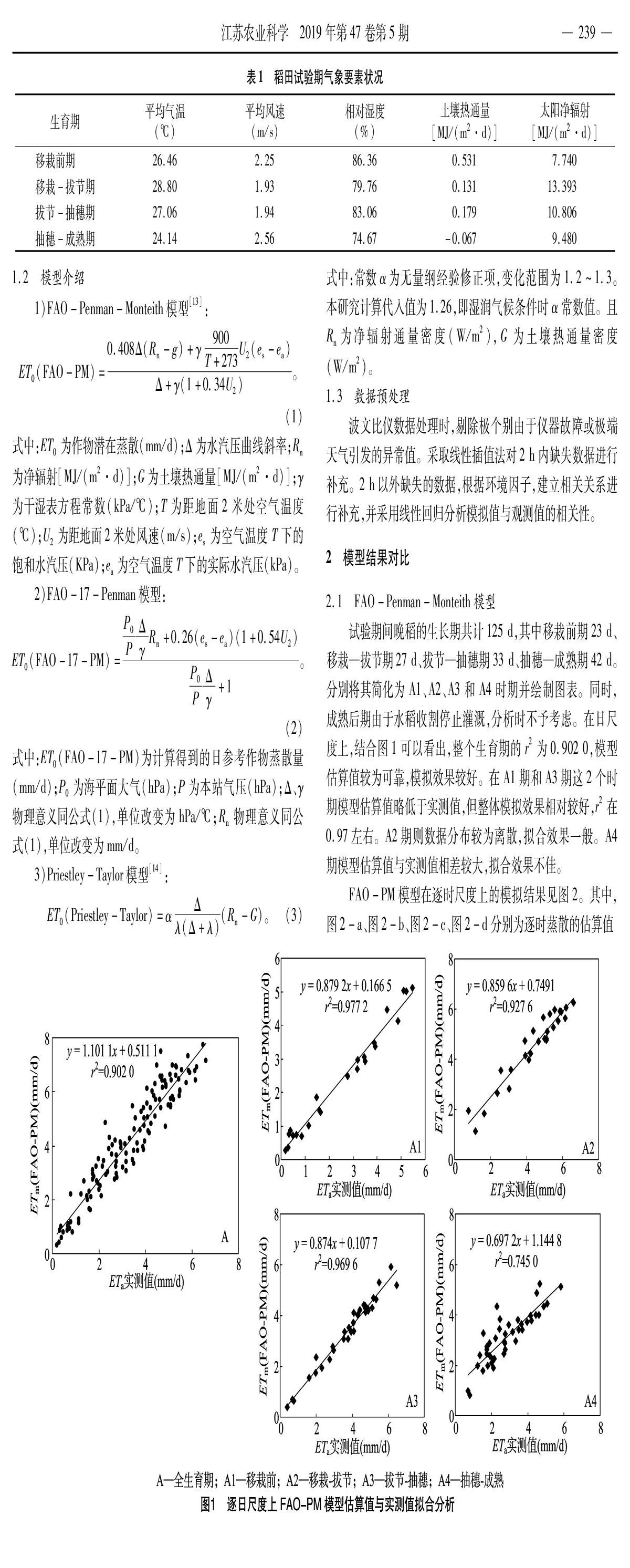
试验期间晚稻的生长期共计125 d，其中移栽前期23 d、移栽—拔节期27 d、拔节—抽穗期33 d、抽穗—成熟期42 d。分别将其简化为A1、A2、A3和A4时期并绘制图表。同时，成熟后期由于水稻收割停止灌溉，分析时不予考虑。在日尺度上，结合图1可以看出，整个生育期的r2为0.902 0，模型估算值较为可靠，模拟效果较好。在A1期和A3期这2个时期模型估算值略低于实测值，但整体模拟效果相对较好，r2在0.97左右。A2期则数据分布较为离散，拟合效果一般。A4期模型估算值与实测值相差较大，拟合效果不佳。

FAO-PM模型在逐时尺度上的模拟结果见图2。其中，图2-a、图2-b、图2-c、图2-d分别为逐时蒸散的估算值

与实测值4个不同时期的拟合情况，图2-e为整个生育期的拟合情况。在时间尺度由逐日降为逐时后，模型的适用性明显降低，各时期的r2下降到0.6～0.7，斜率K升至1.66～219。在实测值高于0.3 mm/h时，估算值和实测值之间的偏差更加明显。风速突变是导致模型适用性降低的一个可能原因。逐时尺度上空气动力项相比于辐射动力项更不稳定，当风速发生突变，可能会导致FAO-PM模型的估算值大幅度偏离实测值。因此，在逐时尺度上，FAO-PM模型并不适合用来估算该地区的作物蒸散。

2.2 FAO-17-Penman模型

模型FAO-17-Penman在逐日尺度上的拟合情况见图3。以B代表全生育期，移栽前期、移栽—拔节期、拔节—抽穗期、抽穗—成熟期分别为B1、B2、B3和B4时期。整个生育期r2为0.864 3，数据离散程度较大，模拟蒸散值与实测蒸散值拟合效果不太理想。但在B1期和B3期，r2在0.97左右，斜率在1.04左右，这2个时期估算值虽然略高于实测值，但拟合程度较高，模拟效果较好。B2期拟合效果相较于B1和B3略差，数据分布也较离散，模拟效果一般;B4期r2为 0.662 7，估算值与实测值相差较大，过高估计了实际蒸散，效果不佳。将逐日尺度上的FAO-PM模型与FAO-17-Penman模型相比较而言，显然FAO-PM模型的精确度更高。

图4为逐时尺度上的不同時期估算值与实测值的拟合情况，可以发现相比于逐日尺度，逐时尺度上FAO-17-PM模型的适用性也明显降低。整个生育期的r2下降，前3个时期的相关系数r2下降到0.7～0.8之间，抽穗—成熟期的r2仅为0.043 8。同时，估算值高出实测值的比例比逐日尺度上高出更多，误差更大。当实测蒸散值高于0.2 mm/h时，模拟值偏离实测值较多。在逐时尺度上，稻田在抽穗期前，使用FAO-17-PM模型能大概反映70%～80%的实际蒸散情况，但是在进入抽穗—成熟期后，该模型不再适合模拟该地区的估算作物蒸散，偏差较大。

2.3 Priestley-Taylor模型

模型Priestley-Taylor在逐日尺度上的拟合情况见图5。以C代表全生育期，移栽前期、移栽—拔节期、拔节—抽穗期、抽穗-成熟期分别为C1、C2、C3和C4时期。从整个生育期来看，r2为0.940 9，数据在1 ∶ 1线左右分布较均匀，表明估算蒸散值与实测蒸散值拟合效果很好，模型估算值较为可靠。在移栽前期（C1期）和拔节—抽穗期（C3期），r2均高于0.97，斜率K接近1，模型的相关性甚至要优于全生育期。即使是模拟效果相对不佳的C2与C4期，也要优于同尺度的FAO-17-PM模型和FAO-PM模型。

逐时尺度上Priestley-Taylor模型见图6，降尺度后模型适用性提高。4个不同生育期的r2均达 0.98 以上，表明在逐时的时间尺度上，Priestley-Taylor模型的估算效果较好，可以反映实际情况的98%以上，模型估算值与实测值极为接近。斜率K在0.97～1.05之间，相对偏差较小。实际蒸散量的范围在0.4 mm/h以下时，估算值与实测值的重合度较高，在蒸散量超过0.4 mm/h时，模拟值略高于实测值。总的来说，在逐时尺度上，相比于FAO-17-PM模型和FAO-PM模型，Priestley-Taylor模型的模拟效果更好，能很好地反映当地稻田的实时蒸散发状况。

2.4 模型对比

将FAO-PM模型和FAO-17-PM模型的估算值进行对比，结果见表2。

逐日尺度上，FAO-PM模型全生育期的估算累积值与实测累积值的相对偏差仅为0.26%，移栽前期与拔节—抽穗期的相对偏差都为负值，说明这2个时期模型低估了实际蒸散，而移栽—拔节期与抽穗—成熟期的相对偏差分别为3.07%和9.88%，说明这2个时期模型高估了实际蒸散。逐日尺度上FAO-17-PM模型各时期的估算累积值都高于实测累积值，全生育期的相对偏差为20.87%。综合来看，2种模型估算蒸散值趋势一致但差异明显，FAO-17-PM模型的估算累积值在各个时期都高于FAO-PM模型累积值，这与龚元石等的研究结果[15]一致。同时，FAO-PM模型相比FAO-17-PM模型拟合效果更优，与实测值更为接近。多数学者认为造成这2个模型估算值之间差异的主要原因是其空气动力项和辐射动力项采用了不同的参数。刘倪等认为在某些地区，FAO-17-PM模型是可以代替FAO-Penman-Monteith对参考作物蒸散量进行计算的，但是需要对风速进行修正，不同的修正式可能结果迥异，因此在气象数据相对完整的情况下使用FAO-PM模型更为合适[16]。逐时尺度上FAO-PM模型和FAO-17-PM模型估算值在各个时期都高于实测值过多，同时2个模型之间差异更加明显。降尺度后FAO-17-PM模型估算值偏移实测值的趋势加大，抽穗—成熟期估算累积值甚至接近实测累积值的8倍，模型适用性大幅度降低。同样FAO-PM模型的适用性也随尺度降低而大幅度下降，模型整体高估了实际蒸散过多，在实测值高于0.3 mm/h时，估算值和实测值之间的偏差更加明显。因而FAO-17-PM模型与FAO-Penman-Monteith模型都不适合用于该地区的逐时蒸散模拟。袁小环等认为PM模型易受到风速变化影响，而时尺度上空气动力项相比于辐射项变化更为剧烈，因而可将风速突变作为PM模型降时间尺度适用性降低的一个可能原因，但具体各时期是否为模型主导因子还需进一步的试验测定[17]。

Priestley-Taylor模型建立在平衡蒸发理论基础上，所需气象资料较少，它与FAO-Penman-Monteith模型、FAO-17-PM模型的主要区别在于，后两者考虑了空气动力项，而前者没有。表2显示了PT模型与其他2种PM模型的模拟差别。逐日尺度上PT模型模拟效果不及FAO-PM模型，但优于FAO-17-PM模型。模型全生育期的蒸散估算累积值与实测累积值的相对偏差为11.72%，在可接受范围内。移栽前期与拔节—抽穗期的相对偏差分别为5.78%和2.80%，r2均高于0.97，估算值与实测值的重合度较高，模型拟合效果很好。综合认为逐日尺度上PT模型的适用性较好，可用于该地区逐日尺度的蒸散监测。时间尺度由逐日降为逐时后，PT模型整体适用性提高。4个生育期r2均达0.98以上，全生育期估算累积值和实测累积值的相对偏差为 7.38%。整体来看，逐时尺度上3种蒸散模型以Priestley-Taylor法的估算结果最优，更适合用于该地区稻田实时蒸散研究。在试验区所处的气候条件，综合2种时间尺度，PT模型较之PM模型，适用性更为稳定，与当地的实际蒸散更为接近，这与米娜等的研究[18]一致。同时许多研究也表明α=1.26 具有广泛性，应用于不同的区域都得到了较为理想的结果[19]。

3 结论

在晚稻整个生长期间，各模型估算值与波文比计算值的整体变化趋势一致。就单一生育期而言，相对湿度较高的移栽前期与拔节—抽穗期拟合效率普遍高于其他時期，模型估算值与实测值也更为接近。初步判断各时期的气象因子是造成各生育时期模拟效果差异的可能原因，但它们对模型的具体影响作用有待进一步研究。

不同时间尺度上各模型估算蒸散值与实测值的的拟合效率差别较大。逐时尺度上按效率比较，Priestley-Taylor模型>FAO-PM模型>FAO-17-PM模型，因此Priestley-Taylor模型的拟合效率最高，最适合用于当地稻田蒸散的实时预测。同样逐日尺度上的拟合效率，FAO-PM模型>Priestley-Taylor模型>FAO-17-PM模型，因此逐日尺度上的蒸散预测以FAO-PM模型为宜。

模型参数的选取和下垫面的性质会对模型精度产生一定的影响。本研究PT模型α的取值为1.26，在试验区所处的湿润气候条件下，能较精确地估算出稻田的蒸散量，特别是在逐时尺度，田间相对湿度较高的移栽前期和拔节—抽穗期，PT模型的优势更为显著。Priestley-Taylor模型与PM模型之间的主要差别在于，前者忽略了空气动力项，而后者没有。风速在小时尺度上的突变是导致逐时尺度下模型FAO-PM与FAO-17-PM整体适用性降低的一个可能原因。同时FAO-PM模型与FAO-17-PM模型相比较，后者考虑到了彭曼模型中一些参数的修正，但显然参数修正反而降低了模型精度，因而FAO-17-PM模型并不适合用于当地的稻田蒸散量模拟。

4 讨论

第一，模型采用的作物系数由FAO提供而非实际测量，有可能对估算值精度产生影响，需要进一步进行田间观测修正。此外蒸散模型的时间尺度效应还会受到冷、暖季的气候条件影响[11]，所以还需将早稻与晚稻数据进行对比研究，以便更深层次了解稻田蒸散的尺度效应。第二，稻田蒸散模型的时间尺度研究，不仅仅局限于小时尺度与日尺度的精度对比，未来更有望走向建立不同时间尺度的转换模型，实现瞬时向日尺度的扩展，以及日尺度向旬或是更大尺度的转换。参考文献：

[1]贾秋洪，景元书，景梽淏. 典型小流域气候变化及其对潜在蒸散量的影响[J]. 中国农村水利水电，2016（1）：1-7，11.

[2]王 东. 栅格蒸散发模型在区域蒸散发时空分布模拟中的应用研究[J]. 水利技术监督，2016，24（2）：53-55.

[3]丁加丽，彭世彰，徐俊增，等. 基于Penman-Monteith方程的节水灌溉稻田蒸散量模型[J]. 农业工程学报，2010，26（4）：31-35.

[4]白玲晓，王 勇，李 兴，等. 作物蒸散量测定与计算方法研究综述[C]. Intelligent Information Technology Application Association.Proceedings of 2011 AASRI Conference on Information Technology and Economic Development（AASRI-ITED 2011 V3），2011：6.

[5]李 琴，陈 曦，包安明，等. 基于SEBS模型干旱区蒸散发量研究[J]. 遥感技术与应用，2014，29（2）：195-201.

[6]Kustas W P，Choudhury B J，Moran M S，et al. Determination of sensible heat flux over sparse canopy using thermal infrared data[J]. Agricultural&Forest Meteorology，1989，44（3/4）：197-216.

[7]强小嫚，蔡焕杰，王 健. 波文比仪与蒸渗仪测定作物蒸发蒸腾量对比[J]. 农业工程学报，2009，25（2）：12-17.

[8]Arnold J，Srinivasan R，Neitsch S，et al. Soil and water assessment tool（SWAT）：global applications[R]. 2009.

[9]Zhang L，Lemeur R. Evaluation of daily evapotranspiration estimates from instantaneous measurements[J]. Agricultural & Forest Meteorology，1995，74（1/2）：139-154.

[10]杨汉波，杨大文，雷志栋，等. 任意时间尺度上的流域水热耦合平衡方程的推导及验证[J]. 水利学报，2008，39（5）：610-617.

[11]杨秀芹，钟平安. 基于两种时间尺度气象资料计算的参考作物蒸散量对比分析[J]. 中国农业气象，2011，32（2）：214-219.

[12]魏新光，陈滇豫，汪 星，等. 山地枣林蒸腾主要影响因子的时间尺度效应[J]. 农业工程学报，2014，30（17）：149-156.

[13]李玉霖，崔建垣，张铜会. 参考作物蒸散量计算方法的比较研究[J]. 中国沙漠，2002，22（4）：372-376.

[14]刘晓英，林而达，刘培军. Priestley-Taylor与Penman法计算参照作物腾发量的结果比较[J]. 农业工程学报，2003，19（1）：32-36.

[15]龚元石. Penman-Monteith公式与FAO-PPP-17 Penman修正式计算参考作物蒸散量的比较[J]. 北京农业大学学报，1995（1）：68-75.

[16]刘 倪，夏 伟，吴晓蔚，等. 几种参考作物蒸散量计算方法的比较[J]. 河北科技大学学报，2009，30（1）：17-24.

[17]袁小环，杨学军，陈 超，等. 基于蒸渗仪实测的参考作物蒸散发模型北京地区适用性评价[J]. 农业工程学报，2014，30（13）：104-110.

[18]米 娜，陳鹏狮，张玉书，等. 几种蒸散模型在玉米农田蒸散量计算中的应用比较[J]. 资源科学，2009，31（9）：1599-1606.

[19]Utset A，Farre I，Martinez-Cob A，et al. Comparing Penman-Monteith and Priestley-Taylor approaches as reference evapotranspiration inputs for modeling maize water-use under Mediterranean conditions[J]. Agricultural Water Management，2004，66（3）：205-219.王乐乐，郑讯涛，张寓涵，等. 总固体浓度对猪粪厌氧消化的影响及菌群结构分析[J]. 江苏农业科学，2019，47（5）：244-248.