平面混凝土框架结构地震损伤机理研究

游励晖 刘 伟 邵长江 李吉林 钱永久

(1. 中铁二院工程集团有限责任公司， 成都 610031；2. 西南交通大学， 成都 610031；3. 中国国家铁路集团有限公司， 北京 100844)

一般认为，梁柱框架结构的地震损伤形态主要是剪切破坏，如建筑的传统分析方法是分析结构底部的剪力需求，并根据结构的抗剪能力进行抗震性能判断。但最新研究表明[1]，结构自重产生的轴力对抗震性能有重要影响，轴力增大在一定程度上导致抗剪能力降低，抗剪性能的下降又导致轴向抗力减少，两者的相互作用最终导致结构承载能力的丧失。

本文认为混凝土结构承载能力的降低源于材料性能的劣化。混凝土的损伤机制主要是各种微裂纹和微空洞的形成、扩展，以至形成宏观裂纹。在材料内部应力进入塑性阶段，产生永久变形的同时，伴随着材料刚度的降低，在宏观上表现为结构变形增大，承载能力降低。因此，损伤的实质是一种不可逆的能量耗散过程，该过程与材料内部微观组织结构的改变相关，反映了物质状态的变化历程。损伤的终极状态是结构形成的架构退出工作并倒塌。因此结构体系在地震作用下的破坏是一个渐进过程，鉴于传统经典弹塑性模型处理刚度降低和断裂力学模型模拟一点上任意开裂的困境，本文认为损伤力学是分析这一历程的有力工具和较好选择。

在激励及边界条件、结构类型已知的情况下，材料的本构方程是影响结构响应的根本原因。本文基于标量损伤变量和能量范数损伤准则，推导了满足热力学第二定律的塑性损伤本构，并根据Drucker-Prager型屈服函数的关联流动准则，推导了相应的塑性参数和一致切线模量。在此基础上，计算混凝土框架梁柱的弹塑性损伤响应，与振动台测试结果进行对比，结果表明，材料损伤表现为拉压的联合作用下材料性能的不断劣化，而梁柱结构的损伤破坏则表现为剪切和轴压联合作用下混凝土柱子的承载力丧失。

1 混凝土塑性损伤本构模型

1.1 损伤本构

损伤材料的Helmholtz比自由能一般设为应变、损伤变量、温度等的函数，考虑到混凝土的拉压异性，实际混凝土材料在循环荷载作用下的损伤是拉压作用的耦合，不考虑作用反向时刚度的恢复系数，刚度降低系数：

d=1-(1-dc)(1-dt)

(1)

式中：dt、dc——拉压状态下的损伤变量。

以Ψ0表示无损状态的自由能，当不考虑温度影响时，混凝土的各向同性损伤的Helmholtz自由能Ψ可表述为应变ε、塑性应力σp、内变量q以及损伤变量d的函数[2-4]。

Ψ(ε,σp,q,d)∶=(1-d)Ψ0(ε)+Ξ(q,σp)

(2)

满足热力学第二定律，则熵产非负，可得本构关系：

(3)

1.2 屈服准则

摩擦型材料的屈服函数为应力张量不变量的标量函数和粘性系数的方程，考虑混凝土材料在压拉作用下的性能差异，用cs(s=c,t分别表示受压和受拉两种受力情况)表示与损伤相关的粘性强度。采用Drucker-Prager型损伤屈服准则，考虑后继屈服的随动硬化效应，以应力不变量的形式表示如下[2]：

(4)

式中：α——待定强度系数。

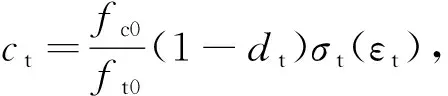
2 损伤变量及损伤准则

损伤变量是物质结构某种不可逆变化的定量表示，是热力学的内变量。损伤变量取决于材料的体积应变和等效累积塑性应变，为计算方便，可以应力或应变形式表示损伤发生的界限值。

(5)

代入自由能表达式，得：

(6)

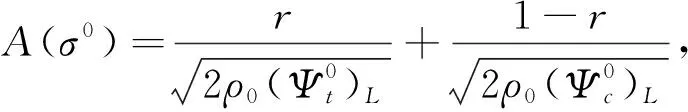
(7)

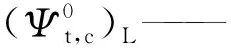
[x]——McAuley函数；

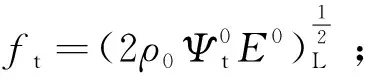
ρ0——初始密度；

E0——初始弹性模量。

代入损伤准则表达式，则有：

(8)

依照Simo的思想[6]，给出式(8)的等效形式：

Fe=G(σe)-G(fs)≤0

(9)

则损伤变量的演化方程表示为：

(10)

由一致性条件，得：

(11)

式中：G(σe)——等效应力的函数，而等效应力为结构当前耗能和材料断裂能有关[7]。

晏殊长期以来得不到公正、合理的评价，受到严重的“污名化”，与大量真相被严重遮蔽或者错误释读有关之外，传统的君子小人、非白即黑以及党争思维方式，也具有相当大的负面影响。

对于抗震结构，可通过粘弹性考虑结构在动力荷载作用下的阻尼效应，此时总应力σT为：

(12)

式中：σv——阻尼应力；

Cs——阻尼参数；

则应力应变的增量关系为：

(13)

(14)

式中：I——单位张量；

Dv——考虑阻尼的损伤张量；

σ0——无损伤应力张量；

3 算例分析

根据上述算法编制了基于ABAQUS的用户材料子程序，通过自定义变量输出得到结构的损伤变量演化曲线，考察结构关键部位在地震激励下及地震结束后的损伤状况，研究结构损伤破坏的物理机制，为混凝土结构的抗震设计提供参考。选取三柱式框架梁的结构为研究对象，其加载及配重情况如图1所示，振动台台面输入地震波如图2所示。

图1 结构加载及配重情况图

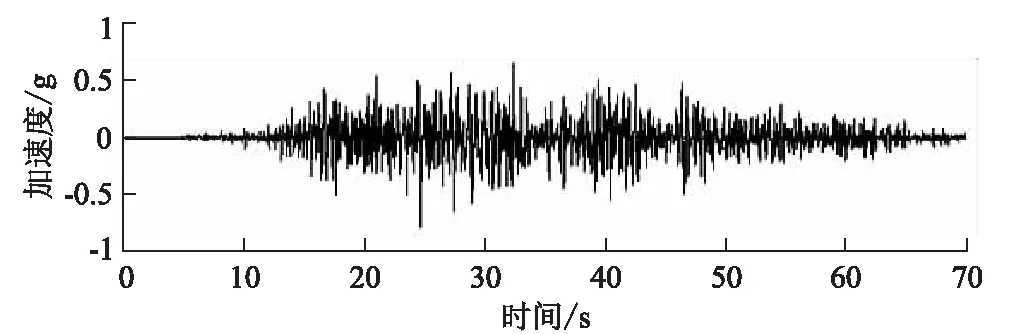
图2 振动台台面地震波

采用上述损伤本构模型，建立有限元模型，模拟混凝土框架模型在地震下的振动行为和损伤模型。计算过程中用平面单元模拟混凝土结构，地震荷载为振动台面的实测加速度时程，主要参数的取值可参见文献[1-2]。

中间柱子顶部损伤如图3所示，其顶部外侧和内部地震损伤演化曲线如图4、图5所示。

图3 中间柱子顶端24.9 s时的损伤状态图

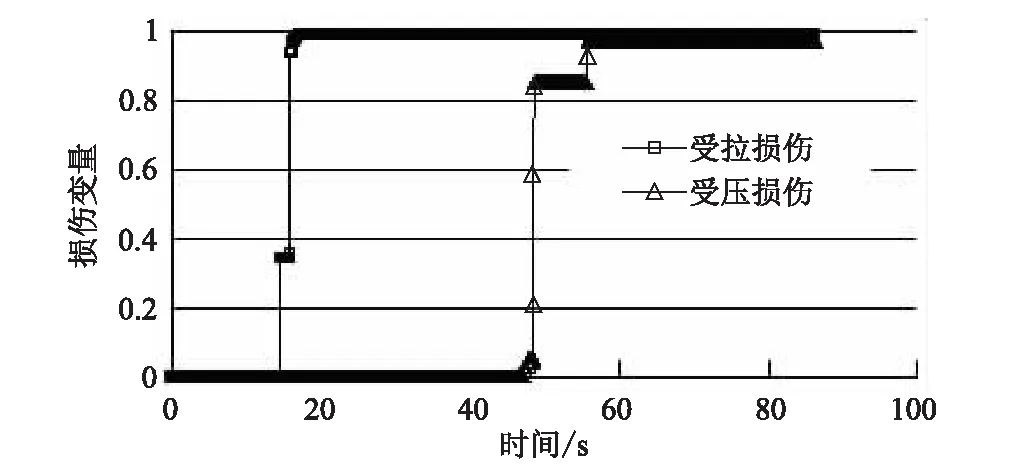
图4 中柱柱顶外侧单元损伤变量演化图

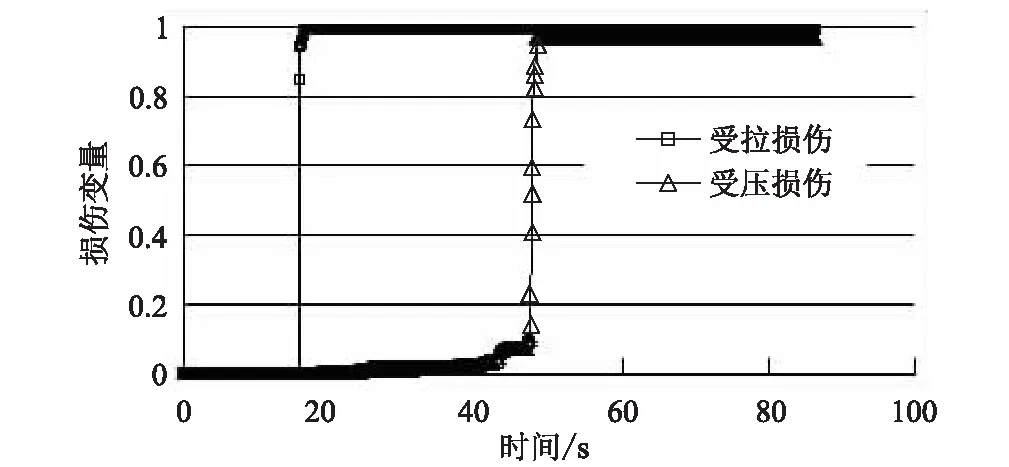
图5 中柱柱顶中间单元损伤变量演化图

4 结论

(1)采用混凝土损伤本构模型模拟混凝土框架结构的损伤机制，能够从本构上反映材料力学性能劣化对结构承载能力降低的影响，在不考虑失稳影响的情况下，可以反映强度特性是结构倒塌影响的物理机制之一。

(2)对于上部较重的混凝土结构体系，重力对结构的倒塌破坏有着重要的影响。高耸结构以及部分大跨度桥梁结构的抗震设计，应考虑响应过程中轴力对承载力降低的影响。

(3)从损伤变量的演化曲线可以看出，结构材料的损伤变量是一个非减量，反映了损伤的累积效应，考虑混凝土材料拉压异性(受拉损伤先于受压损伤出现并迅速发展)，损伤本构适于地震作用下结构响应的模拟分析。