5G NR随机接入信号的规划研究
张建国,韩春娜,杨东来(.华信咨询设计研究院有限公司,浙江杭州3005;.诺基亚上海贝尔股份有限公司,浙江杭州30053)
0 引言
5G NR的随机接入过程与LTE类似,也包括随机接入过程初始化、随机接入资源选择、随机接入信号发射、随机接入响应接收和竞争解决等步骤。其中随机接入资源选择包括选择随机接入信号的前导码、初始发射功率、频率等,随机接入资源选择直接影响了随机接入的成功率。本文接下来主要分析随机接入信号的规划,包括与设计密切相关的PRACH前导格式规划、Ncs规划和根序列规划。
1 随机接入前导序列
随机接入前导(random access preamble)序列由具有零相关区的Zadoff-Chu序列(ZC-ZCZ)产生,而ZCZCZ序列由1个或多个根Zadoff-Chu序列产生。随机接入前导xu,v(n)根据式(1)和式(2)产生。
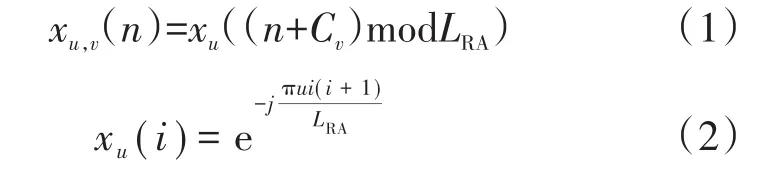
式中:
u——ZC序列的根序列(以下简称根序列),取值是0~837或0~137
LRA——ZC序列的长度,取值是839或139
Cv——ZC序列的循环移位(CS——Cyclic Shift),Cv的数值与限制集合类型、循环移位Ncs等有关
i——取值是0,1,…,LRA-1
ZC序列的长度不同,应用的频率范围(FR——Frequency Range)也不同,LRA=839应用于 FR1(450~6 000 MHz),随机接入前导的子载波间隔ΔfRA是1.25 kHz或者5 kHz;LRA=139应用于FR1(450~6 000 MHz)和FR2(24 250~52 600 MHz),ΔfRA=15×2μkHz,其中μ∈{0,1,2,3}。本文只讨论LRA=839这种情况。
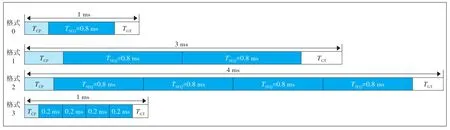
图1 PRACH前导格式
2 PRACH前导格式规划
PRACH在时域上由CP(长度是TCP)、1个或多个随机接入前导(单个随机接入前导的长度是TSEQ)和保护时间(长度是TGT)3部分组成。CP的长度与时延扩展有关,长的CP允许更大的时延扩展,因此可以支持更大的小区半径。单个随机接入前导的长度TSEQ与随机接入前导子载波间隔ΔfRA的关系为TSEQ×ΔfRA=1,总的序列长度影响基站对随机接入前导的接收质量,更长的序列长度意味着基站能够接收更多的能量,从而获得更好的解调性能。保护时间内不发送任何信号,保护时间决定了小区的最大覆盖半径,即小区的最大覆盖半径=c×TGT/2,其中c=3×108m/s。
根据CP、随机接入前导、保护时间以及ΔfRA的不同,PRACH前导格式分为4种,分别是格式0~3,如图1所示。PRACH前导格式规划即根据小区覆盖半径、应用场景等来选择合适的PRACH前导格式。
PRACH前导格式0的长度是1 ms,CP、随机接入前导、保护时间的长度分别是0.103、0.8、0.097 ms,子载波间隔ΔfRA=1.25 kHz,小区的最大覆盖半径是14.53 km。格式0适合于正常半径的小区覆盖,如市区、农村和郊区等环境。
PRACH前导格式1的长度是3 ms,CP、随机接入前导、保护时间的长度分别是0.684、2×0.8=1.6、0.716 ms,子载波间隔ΔfRA=1.25 kHz,小区的最大覆盖半径是107.34 km。格式1的随机接入前导重复2次,在较低的SINR下有较好的接收质量,且CP和保护时间最大,因此适合于大的小区半径,如海面、沙漠等环境。
PRACH前导格式2的长度是4 ms,CP、随机接入前导、保护时间的长度分别是0.153、4×0.8=3.2、0.647 ms,子载波间隔ΔfRA=1.25 kHz,小区的最大覆盖半径是97.11 km。格式2的随机接入前导重复4次,在低的SINR下也有相对较好的接收质量,因此适合于时延扩展小、信号传播损耗大的场景,如深度覆盖等。
PRACH前导格式3的长度是1 ms,CP、随机接入前导、保护时间的长度分别是0.103、4×0.2、0.097 ms,子载波间隔ΔfRA=5 kHz,小区的最大覆盖半径是14.53 km。格式3的子载波间隔较大,对多普勒频移和相位噪声不敏感,因此适合于高速场景。
3 Ncs规划
5G NR的Ncs与随机接入前导的子载波间隔、限制集合的类型有关,如表1所示。Ncs规划即根据小区的最大覆盖半径、限制集合类型、PRACH前导格式等因素选择合适的Ncs配置,以降低小区内随机接入前导发生冲突的概率。
如果不考虑限制集合类型因素,根据小区的最大覆盖半径(假定小区的最大覆盖半径是3 km),确定Ncs配置的过程如下:
a)计算2个循环移位的最小间隔:3 km小区的最大环回时间是3 000/(3×108)×2=20 μs;假定定时误差是 2 μs,多径时延余量是 7 μs;安全余量是 7 μs,则 2个循环移位的最小间隔是20+2+7+7=36 μs。
b)计算Ncs的最小值
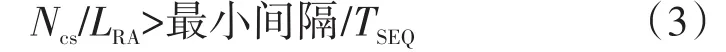
其中,LRA=839;当ΔfRA=1.25 kHz时,TSEQ=800 μs,当ΔfRA=5 kHz,TSEQ=200 μs。根据式(3),可以计算当ΔfRA=1.25 kHz时,Ncs的最小值=「36/800×839⌉=38;当ΔfRA=5 kHz时,Ncs的最小值=「36/200×839⌉=152。
c)查表获得Ncs允许的配置:根据表1,可以看出当ΔfRA=1.25 kHz时,无限制集合、限制集合A和限制集合B允许的最小的Ncs分别是38、38、38,对应的Ncs配置分别是7、5、5。当ΔfRA=5 kHz时,无限制集合、限制集合A允许的最小的Ncs分别是209、152,对应的Ncs配置分别是13、11。
根据以上分析,可以得出以下2个结论:
a)在其他参数相同的条件下,小区的最大覆盖半径越大,Ncs也越大。
b)在其他参数相同的条件下,ΔfRA=5 kHz较ΔfRA=1.25 kHz需要更大的Ncs。
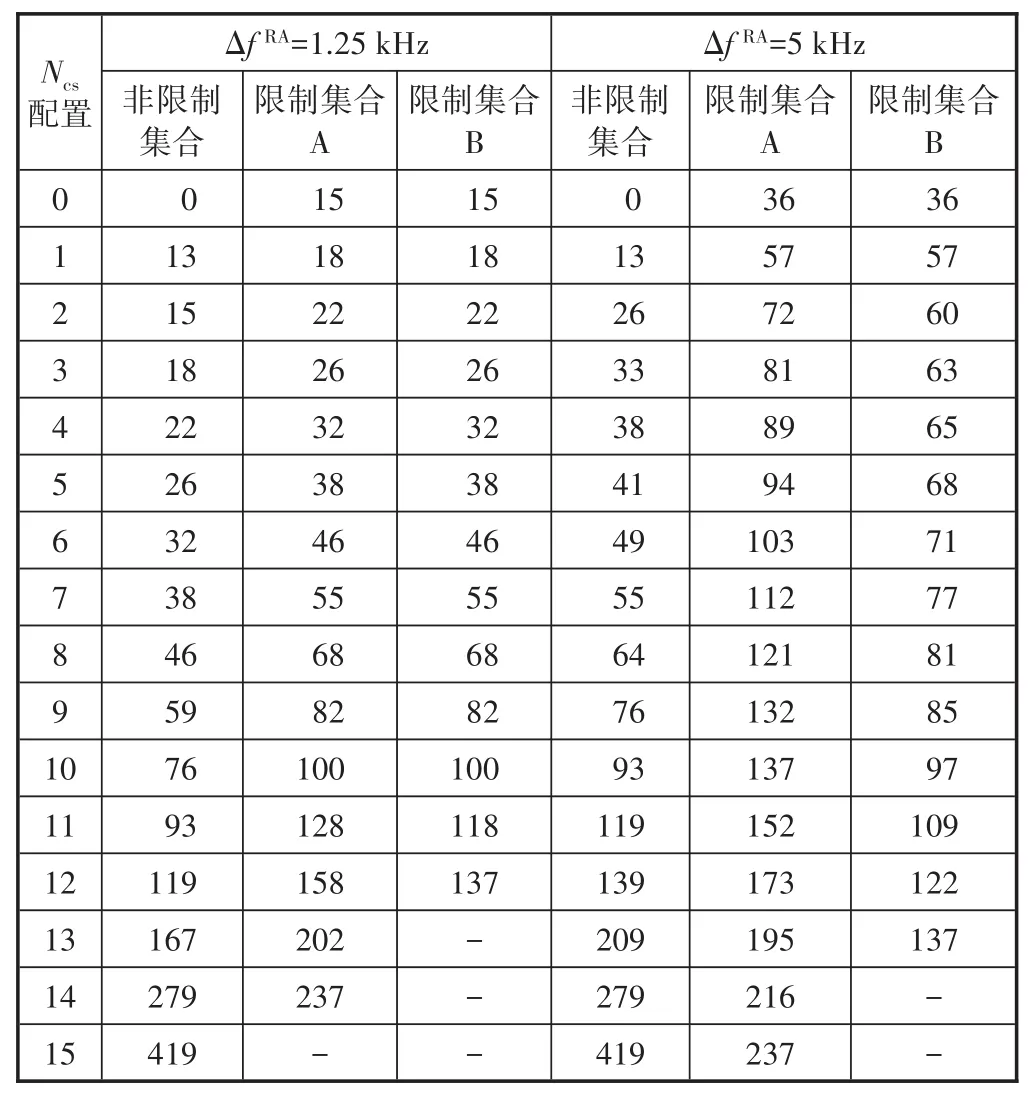
表1 Ncs的配置
4 根序列规划
根据协议,每个PRACH都有64个随机接入前导,这64个随机接入前导首先由某个逻辑根序列索引(该序列索引通过高层参数PRACHRootSequenceIndex发送给UE)对应的根序列通过循环移位的方式得到,并按照可用循环移位Cv的大小进行升序排列,如果PRACHRootSequenceIndex对应的根序列无法产生64个随机接入前导,则逻辑根序列索引加1,其对应的根序列继续产生随机接入前导,如果随机接入前导还不到64个,则逻辑根序列索引继续加1,直至多个连续的逻辑根序列索引对应的根序列产生64个随机接入前导为止。
逻辑根序列索引与根序列u是一对一的映射关系,该映射关系见3GPP TS 38.211协议的表6.3.3.1-3,逻辑根序列索引0~4对应的根序列u分别是129、710、140、699、120。
根序列的规划包括计算逻辑根序列索引的范围和计算每个小区配置的根序列数量2个部分,主要是为相邻小区配置不同的根序列,以便降低小区间随机接入前导发生冲突的概率。由于随机接入前导是通过根序列的循环移位获得的,本文接下来不严格区分循环移位和随机接入前导这2个概念。
4.1 逻辑根序列索引的范围
逻辑根序列索引的范围与限制集合类型有关。5G NR有无限制集合、限制集合A和限制集合B 3种类型,与LTE类似,无限制集合适用于UE移动速度慢的小区,限制集合A和B适用于UE移动速度快的小区。
对于无限制集合,逻辑根序列索引的范围是0~837。
对于限制集合A或B,逻辑根序列索引的范围与Ncs的配置有关,可以通过以下步骤计算限制集合A和B的逻辑根序列索引的范围。
a)根据逻辑根序列索引,通过查找3GPP TS 36.211协议的表6.3.3.1-3得到根序列u,根据式(4)计算出q,q是满足条件的最小非负整数。
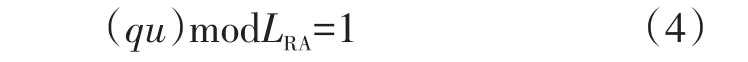
b)根据q,通过式(5)计算出du。
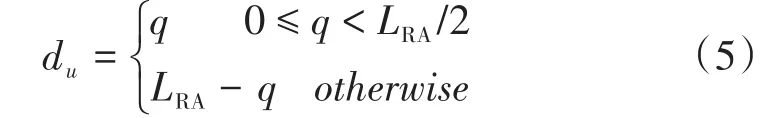
c)对于限制集合A,如果du满足式(6),则该逻辑根序列索引对应的根序列u有可用的随机接入前导,如果du不满足式(6),则该根序列u没有可用的随机接入前导。
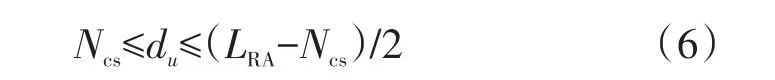
d)对于限制集合B,如果du满足式(7),则该逻辑根序列索引对应的根序列u有可用的随机接入前导,如果du不满足式(7),则该逻辑根序列索引对应的根序列u没有可用的随机接入前导。
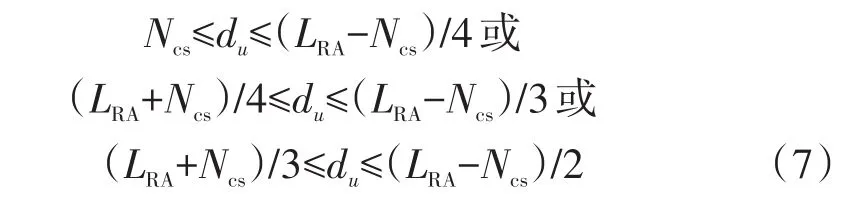
以ΔfRA=1.25 kHz为例来演示限制集合A可用的逻辑根序列索引的计算过程。
假设Ncs的配置是0,则Ncs=15,假设逻辑根序列索引是0,查表可知逻辑根序列索引0对应的根序列u是129,满足式(4)的q是826,根据式(5)计算du=13,du=13不满足式(6),因此,逻辑根序列索引0对应的根序列129不能用于限制集合A。令逻辑根序列索引依次取值1~837,可以发现当逻辑根序列索引是1~23、820~837时,计算得到的du都不满足式(6),当逻辑根序列索引是24~819时,计算得到的du均满足式(6)。因此,当Ncs=15时,可用的逻辑根序列索引的范围是24~819。
依次类推,可以计算当ΔfRA=1.25 kHz、Ncs配置是1~15时,限制集合A可用的逻辑根序列索引的范围。同理,可以计算出当ΔfRA=5 kHz、Ncs配置是0~15时,限制集合A可用的逻辑根序列索引的范围。
依次类推,可以计算当ΔfRA=1.25 kHz和ΔfRA=5 kHz,限制集合B可用的逻辑根序列索引的范围,由于公式(7)中的du在Ncs和(LRA-Ncs)/2之间是不连续的,可用的逻辑根序列索引在0~837是不连续的,限于篇幅,本文不再给出限制集合B可用的逻辑根序列索引的范围。无限制集合、限制集合A可用的逻辑根序列索引的范围如表2所示。
根据表2,可以得出以下结论:对于限制集合A,随着Ncs的增加,可用的逻辑根序列索引的数量逐渐减少,该结论对限制集合B同样适用。
4.2 每个小区配置的根序列数量
由于每个小区的随机接入前导是64个,通过表2获得逻辑根序列索引的范围后,还要计算出每个根序列产生的随机接入前导数量,进而计算出每个小区需要配置的逻辑根序列索引的数量,以确保相邻小区使用不同的随机接入前导,降低小区间随机接入前导发生冲突的概率。
计算每个根序列u产生的随机接入前导数量的步骤如下。
a)对于无限制集合,循环移位Cv通过式(8)产生。
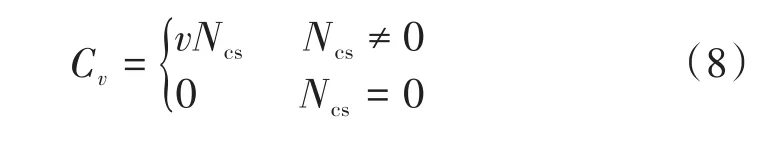
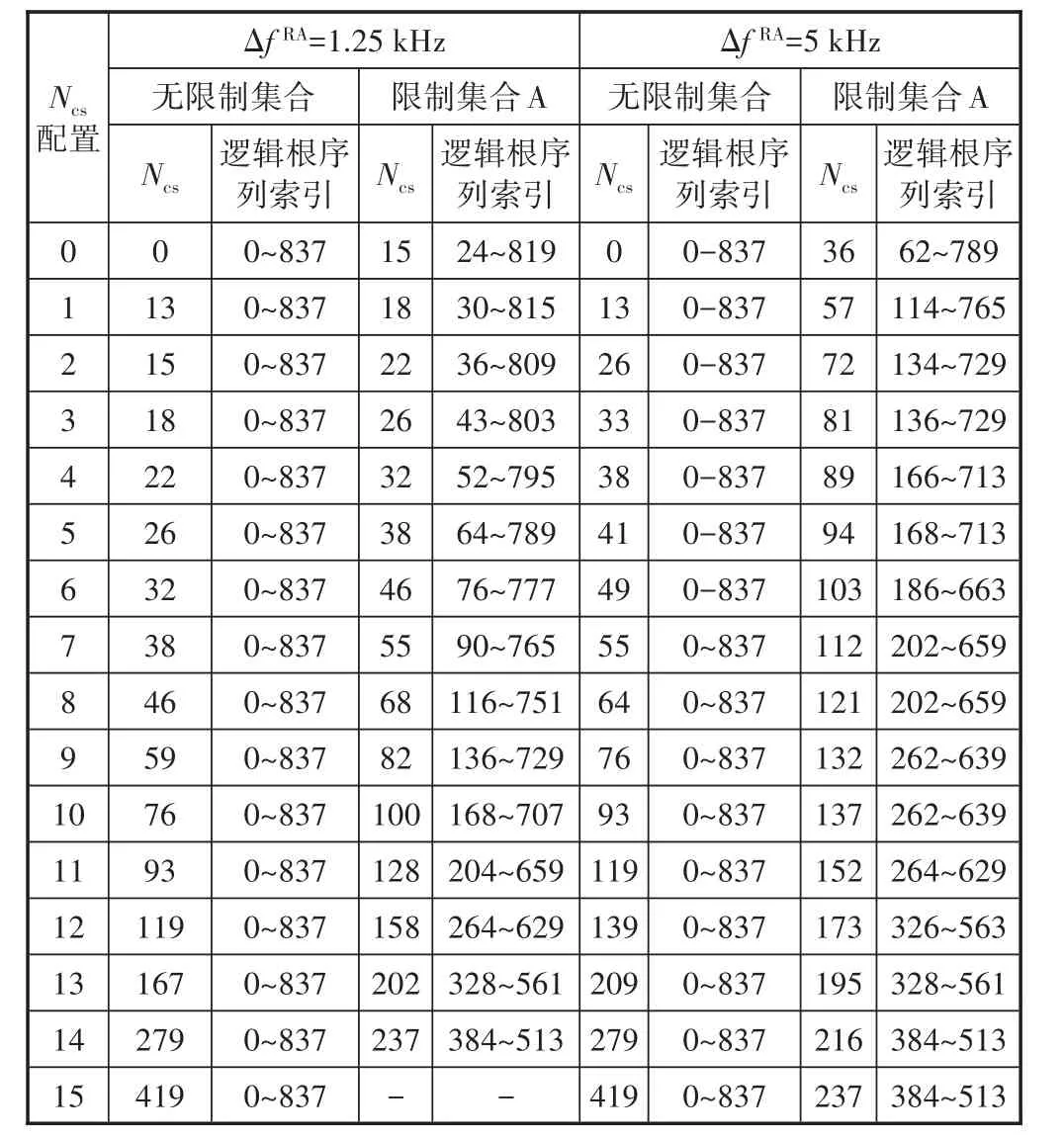
表2 无限制集合、限制集合A可用的逻辑根序列索引的范围
其中,当Ncs≠0时,v=0,1,…,⌊LRA/Ncs」-1。根据式(8),可以计算出1个根序列u产生的循环移位有⌊LRA/Ncs」个。当Ncs=13时,可产生⌊839/13」=64个循环移位,每个小区只需要配置1个逻辑根序列索引即可获得64个随机接入前导。而当Ncs=59时,可产生⌊839/59」=14个循环移位,每个小区需要配置5个连续的逻辑根序列索引才能获得64个随机接入前导。
b)对于限制集合A,循环移位Cv通过式(9)产生。
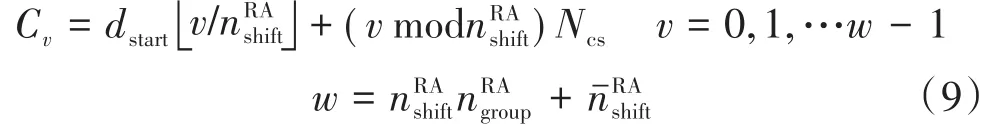
假定Ncs=15,逻辑根序列索引176产生的循环移位共计有2×7=14个,Cv分别是0、15、30、45、60、75、90,341、356、371、386、401、416、434,Cv的组间间隔是251,Cv的组内间隔是15;逻辑根序列索引178产生的循环移位共计有1×6=6个,Cv分别是0、15、30、45、60、75,Cv的组内间隔是15;逻辑根序列索引182产生的循环移位共计有2×7=14个,Cv分别是0、15、30、45、60、75、90,321、336、351、366、381、396、411,Cv的组间间隔是231,Cv组内间隔是15。
假定Ncs=55,逻辑根序列索引176产生的循环移位共计有2×2=4个,Cv分别是0、55、346、401,Cv的组间间隔是291,Cv的组内间隔是55;逻辑根序列索引178产生的循环移位共计有2×1=2个,Cv分别是0、158,Cv的组间间隔是158;逻辑根序列索引182产生的循环移位共计有3×1=3个,Cv分别是0、257、514,Cv的组间间隔是257。
c)对于限制集合B,循环移位Cv通过式(10)获得。
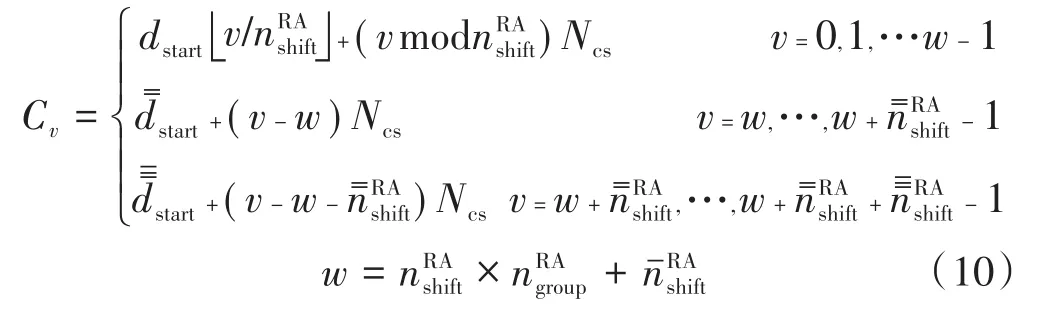
对于限制集合B,根序列u产生的循环移位分为3部分,第1部分有个组,每组有个循环移位,共计有个循环移位;第2部分有个循环移位;第3部分有个循环移位。需要注意的是,多数情况下,和都是 0,只有在(LRA+Ncs)/4≤du≤2LRA/7时,和才有可能都是非 0 的正整数。
假定Ncs=15,逻辑根序列索引364对应的根序列u是58,满足式(4)的q是217,对应的du=217,产生的循环移位共有4×1+1+1=6个,第1部分有4个循环移位,Cv分别是0、44、88、132,Cv的组间间隔是44;第2部分有1个循环移位,Cv是364;第3部分有1个循环移位,Cv是 596。
假定Ncs=15,逻辑根序列索引329对应的根序列是614,满足式(4)的q是220,对应的du=220,产生的循环移位共有3×2+0+0=6个,第1部分有6个循环移位,Cv分别是0、15,71、86,142、157,Cv的组间间隔是66,Cv的组内间隔是15;第2部分和第3部分产生的循环移位个数是0。
根据以上的分析,可以得出以下结论:
a)对于无限制集合、限制集合A和B,随着Ncs的逐渐增大,每个根序列产生的循环移位逐渐减少,为了保证每个小区有64个随机接入前导,需要的根序列的数量随之逐渐增加。
b)对于无限制集合,如果Ncs相同,每个根序列u产生的循环移位的数量也相同。
c)如果Ncs相同或者接近,限制集合A和B产生的循环移位的数量明显少于无限制集合,因此,对于限制集合A和B,每个小区需要分配更多的根序列以产生64个随机接入前导。
d)对于限制集合A和B,循环移位Cv的组内间隔是Ncs,循环移位Cv的组间间隔明显大于Ncs;另外,在其他参数相同的条件下,不同的根序列u产生的循环移位的数量并不相同。
根据结论c),在小区的最大覆盖半径相同的情况下,相对于无限制集合,限制集合A和B需要更多的根序列以保证每个小区有64个随机接入前导,增加根序列后会导致实施的复杂性增加。为了减少复杂度,建议限制集合A和B选择的Ncs,小于根据小区的最大覆盖半径计算得出的Ncs,由于Cv的组间间隔明显大于Ncs,当UE选择的循环移位不在同一个组时,即使Ncs较小,随机接入前导也不会发生冲突。
5 结束语
根据前面的分析,可以发现随机接入信号的PRACH前导格式、Ncs配置、逻辑根序列索引的范围、每个小区配置的根序列数量这几个参数是互相影响的,在规划过程中,要根据实际的网络结构,合理设置随机接入信号的参数,既要降低小区内及小区间的随机接入前导发生冲突的概率,又要尽量减少每个小区的根序列数量,以减少实施的复杂度。

