双站跟踪模式下“嫦娥4号”中继星定轨仿真分析

曹建峰，陈 略，董卫华，段建锋，韩松涛，张 宇

（1.航天飞行动力学技术重点实验室，北京100094；2.北京航天飞行控制中心，北京100094）

引 言

中国探月工程的测控任务采用S 频段统一测控（Unified S-Band，USB）与甚长基线干涉系统（Very Long Baseline Interferometry，VLBI）。“嫦娥 1 号”“嫦娥2 号”任务的测控采用S 频段[1-2]，其后的探测任务则采用X 频段（Unified X-Band，UXB），该频段的测量数据受电离层延迟影响较小。测量频段的提升以及数据处理技术的进步，使得测量数据与轨道计算的精度得到大幅提升[3]。探测任务中，探测器在近地飞行阶段主要由USB/UXB 完成测轨工作，地月转移段后期及环月阶段的测轨由USB/UXB 与VLBI 分系统共同完成。进入使命轨道阶段后，为节省测控资源，测轨则主要由USB/UXB完成，VLBI分系统在轨控前后等关键弧段参与跟踪，以保证测轨精度[2,4]。因而，在使命轨道阶段，探测器的轨道精度相对于在轨测试阶段略有下降。

中国深空网从探月工程二期着手建设，兼顾月球与未来的火星探测任务，初步建成喀什深空站（35 m）、佳木斯深空站（66 m）。探月三期，又补充了南美深空站（35 m），将深空探测测控覆盖率提升至90%[5]。中国深空网亦具备干涉测量跟踪与处理能力，该技术在“嫦娥3号”任务中首次成功运用，并在随后的“嫦娥5 号”试验飞行器进行了连续验证[6-7]。

当前月球探测任务由3 个深空站（喀什、佳木斯、南美）提供支持。受限于星载应答机数量，虽然同一时间多个深空站可共视探测器，但仅能使用1个测站开展上行测轨工作，获取的观测数据类型包括测距、测速和测角。在VLBI 系统不参与跟踪情况下，单站跟踪模式获取的轨道精度受到制约，尤其对于地月平动点探测任务，单站单天的跟踪数据进行轨道解算极易发散。

“嫦娥4 号”中继卫星，又名“鹊桥”（Magpie Bridge），于2018 年5 月发射，使命任务阶段沿地月L2 平动点的Halo 轨道飞行，以完成“嫦娥4 号”着陆器和月球车的地月中继通信支持。基于深空站每日例行的测距、测速测量，以及每周1 次的VLBI 跟踪测量，利用多天连续跟踪数据，“鹊桥”可以实现百米量级的轨道精度，有效完成了在轨运控支持。

先前平动点探测器数据的定轨分析表明，制约轨道精度的一个重要因素是观测几何，通过联合VLBI测量可以有效提升定轨精度[8-9]。轨道解算中，动力学模型误差虽然也在一定程度上影响轨道精度，但相对于观测几何影响较小，比如光压模型10%的误差对10 天的轨道预报影响小于1 km，对于定轨精度的影响大约在百米左右。因此，在现有测控模式下，提高轨道精度的重要途径是UXB与VLBI系统的同时投入跟踪，并尽可能增加有效跟踪弧段。

论文基于现有的深空站资源，对“鹊桥”卫星的测轨能力进行分析，提出利用双站跟踪模式完成测控工作的方式，分析了不同跟踪条件下，双站跟踪模式可能实现的轨道精度，为后续探测任务的实施提供技术依据。

1 观测几何分析

地月L2 平动点近似位于地月连线，距离月球约6.5 万km，绕该平动点的Halo 轨道周期大约为15天[10-11]。为完整地分析对于该类型轨道的观测几何条件，进行为期30天的轨道积分，覆盖大约2个轨道周期。

选取“鹊桥”2018 年6 月20 日的任务轨道，进行30天星历积分，并计算3个深空站的可视弧段，考虑5°的高度截止角，统计每个测站每天跟踪的弧段（图1）与跟踪弧长（图2）。每个深空站都具备每天对“鹊桥”进行7～16 h 的连续跟踪条件。佳木斯与喀什的纬度相当，因而每天可视弧长相近，南美站由于位处南半球，每天可视弧长存在明显的差异。

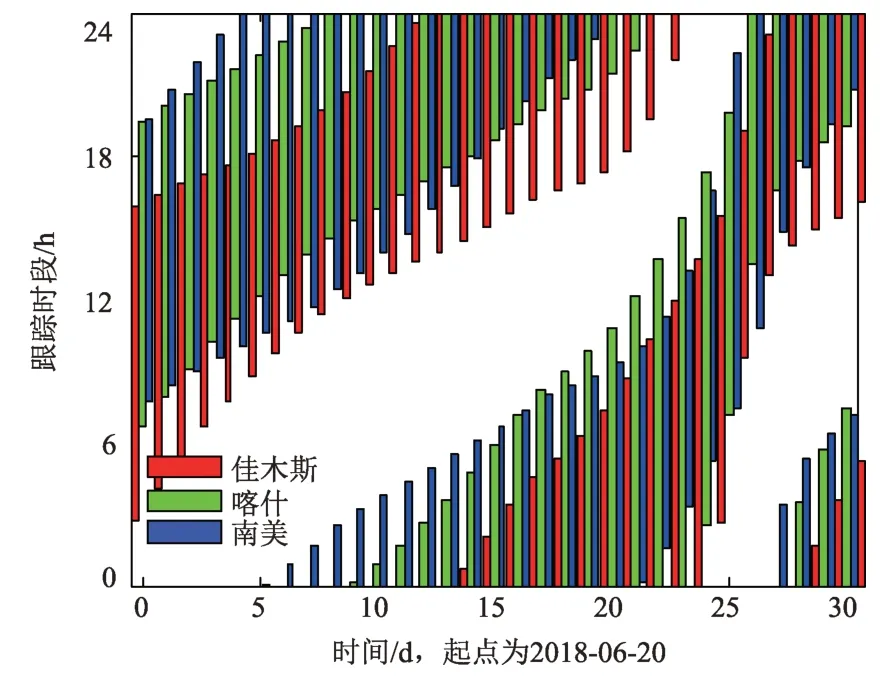
图1 深空站跟踪弧段统计Fig.1 Scheme of tracking arcs for deep space stations

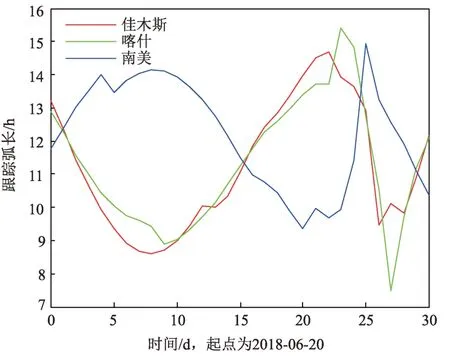
图2 深空站每日跟踪弧长统计Fig.2 Statistics of daily tracking arc length

本文着重于分析双站跟踪模式下的测定轨能力，因此考察跟踪弧段的基本要求为双站共视。图3给出了每日双站共视条件的跟踪弧长，每天最短的共视弧长超过5 h，最长共视弧段约12 h。由于3个深空站的经度与纬度的差异，深空站俩俩共视的弧长差异显著。根据使命轨道阶段的测量安排，每次跟踪弧长为4 h 左右，各种组合的双站观测都可以满足该测控弧长需求。

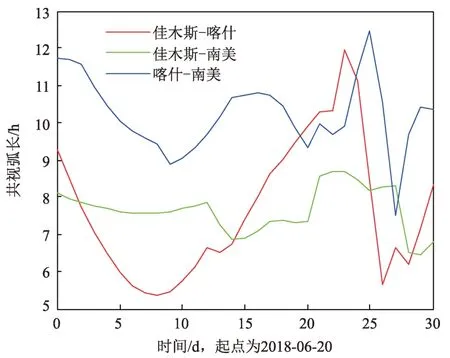
图3 双站共视弧长统计Fig.3 Statistics of tracking arcs for bi-stations

2 观测模型比较

地基站跟踪航天器所获取的测距、测速，以及时延、时延率数据，具有不同的物理意义，对轨道计算精度的贡献也各有差异。

1）测距数据。包括伪码测距、侧音测距，都是描述的无线电信号自测站上行至星载应答机后，再转发下行至地面站，反映的是信号在链路（测站-卫星-测站）的传播距离。对于深空探测器，需要注意采用质心动力学时，测距的观测方程可以表示为[12-13]

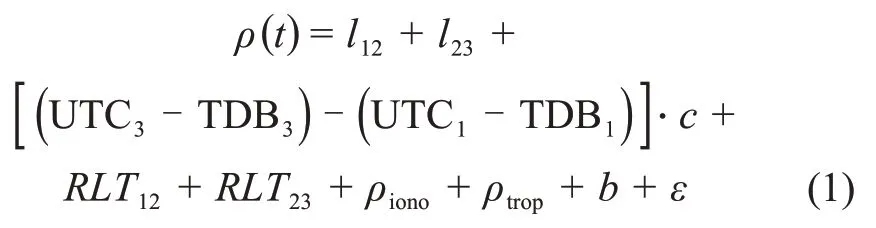
其中：l表示几何距离，下标1，3分别表示上行站和下行站，2 表示星载应答机；TDB为质心动力学时；UTC 为协调世界时；c为光速；RLT表示引力延迟；ρiono为对流层延迟；b表示测量系统误差；ε表示测量噪声。

对于三程测距，仅需将上下行测站设置为相同测站，公式中的项(UTC3- TDB3)-(UTC1- TDB1)可以设置为0。

2）时延观测模型。甚长基线干涉测量是对2 个测站接收到的航天器同一波前信号进行相关处理的一项超高分辨率的天文观测技术，本质反映的是信号到达两个测站的距离之差，时延观测方程可以表示为

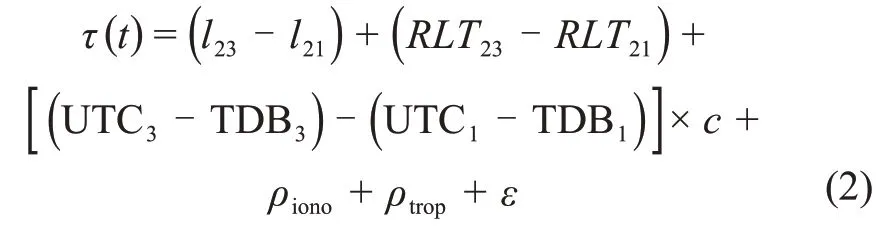
其中，下标1，3分别表示参考站和从站。

3）测速与时延率观测模型。测速和时延率的观测模型可以通过对测距和时延进行差分获取，其观测方程可以表示为

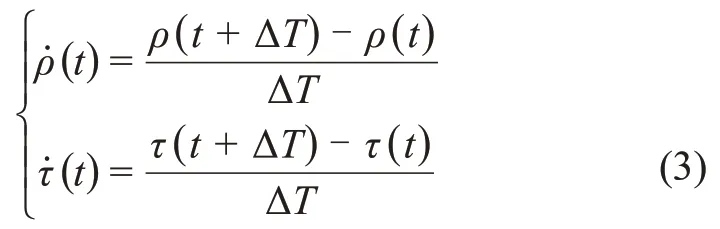
其中，ΔT表示积分周期。

根据测距、测速、时延、时延率的观测方程，测速是测距在时间尺度上的差分，时延则是距离在基线间的差分。因而，对于地月平动点这种速度变化缓慢的轨道，其测速观测对轨道约束有限，轨道计算更需依赖测距与时延数据。

3 仿真分析

考虑到长期在轨管理期间，测控系统不会同时投入3 个深空站对中继星开展跟踪测量，本节仅选取2个深空站进行测定轨能力分析，比较不同跟踪条件下定轨精度。

结合当前深空站数据质量，表1给出了分析采用的动力学模型参数设置，仿真考虑测距数据的随机误差为1 m，测速数据的噪声为0.2 mm/s，测距数据考虑100 m 的系统性误差，VLBI 时延数据的噪声水平为2 ns，不考虑系统误差。实际任务中，VLBI 测量会通过射电源的标校，消除大部分设备延迟影响。

表1 轨道力模型设置Table 1 Setting of dynamical models

3.1 单站测定轨分析

单站跟踪模式下，测站仅能获取双程测距与测速数据。实际数据处理表明，利用单站数据轨道计算极易发散，这是因为探测器与测站相对位置关系变化缓慢，探测器轨道演化、地球公转以及测站随地球的自转在观测数据中的反映极易被测量误差掩盖，即观测数据对轨道变化不敏感，这是环绕型探测不会面临的问题。

使用仿真数据分析结果为：使用单站单天数据，如果不考虑轨道信息的先验约束，轨道迭代发散；考虑轨道先验约束，则轨道精度很大程度上受限于先验轨道的协方差信息（表2）；使用2天以上的数据，可以在不解算测距数据系统误差的前提下进行轨道改进，轨道精度大约比测距数据的系统误差低1 个量级。

表2 单站数据定轨精度Table 2 Orbital accuracy using single station data

3.2 双站测距、测速定轨分析

星上携带1个应答机，因而双站跟踪模式下也仅允许1个测站发射上行信号，多个测站一同接收卫星转发的下行信号，获取双程、三程测距与测速数据。利用双站的测距、测速数据融合解算卫星轨道。

首先分析单天数据，考虑到单天数据迭代解算易发散的事实，分别使用4 h、8 h、12 h 的数据定轨，定轨考虑解算测距数据系统差与不解算2种设置。测量数据不可避免地存在系统性偏差，但对于单天数据，由于观测几何较差，不宜在定轨中解算系统差。即使观测弧段达到12 h，解算系统差的轨道精度远不及不解算的精度（表3）。

表3 单天USB数据定轨精度Table 3 Orbital accuracy using single-day USB data

对于更长弧段的双站测距、测速数据，考虑2～10天的情况，同样分为系统差的解算与不解算2种设置。对于不解算系统差的情况，测距数据的系统差成为影响精度的主要因素，其定轨精度一直稳定在千米量级。2 天以上的跟踪数据可以考虑系统误差的解算，随着跟踪弧段的增加，轨道精度逐步提升。当跟踪弧段达到5天时，仿真定轨精度已经小于动力学模型误差带来的影响，即该情况下有必要考虑动力学模型误差对定轨计算的影响（见表4）。

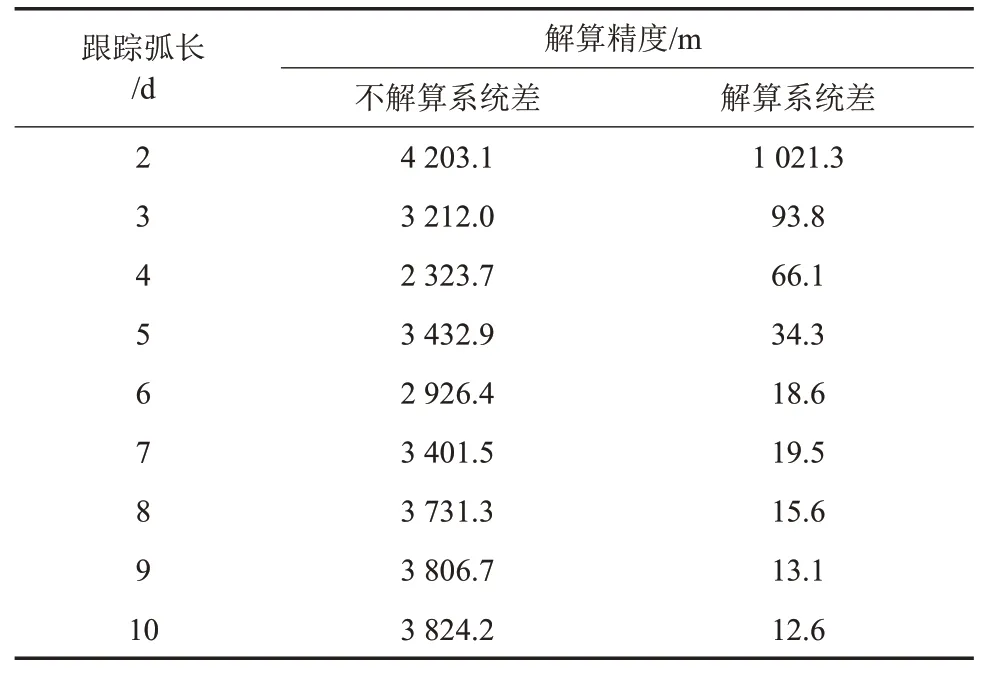
表4 多天USB数据定轨精度统计Table 4 Orbital accuracy using multi-day USB data

3.3 双站测距、测速与VLBI测量定轨分析

双站跟踪模式下，可以获取双程、三程测距、测速以及时延、时延率数据，定轨计算所需的跟踪弧长需求大幅下降。利用单天2/4/6/8/12 h 的跟踪数据分别进行定轨，考虑系统差解算与不解算2组策略，计算结果见表5。在不解算测距数据系统差的情况下，系统差成为制约轨道精度的主要因素，观测弧长的增加并不会显著改善轨道精度；解算系统差的算例中，随着跟踪时间的增加，系统差解算的准确性提高，跟踪弧段达到6 h，系统差解算与仿真设置的偏差小于0.5 m，跟踪弧段的进一步增加，对轨道改进提升有限。

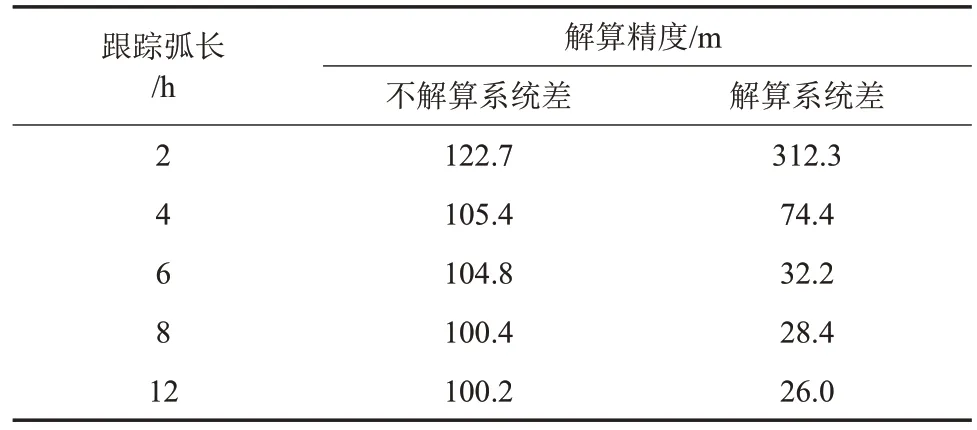
表5 单天双站跟踪模式下定轨精度统计Table 5 Statistics of orbital accuracy using single-day double stations tracking data

当跟踪弧段达到6 h 后，轨道解算精度已经达到30 m，小于动力学模型误差带来的误差影响，因此，需要进一步考虑动力学模型的误差对轨道计算的影响。对6 h 以上的跟踪数据，进行光压系数的解算，表6给出了相应的轨道解算精度，其中1～3组结果采用单天连续跟踪，第4～5组包括2天跟踪数据，每天跟踪6/8 h，第6～7 组包括3 天跟踪数据，每天跟踪6/8 h。使用单天的数据，弧段的增加会显著改善轨道；多天跟踪条件下，当天数增加到3天时，轨道解算精度趋于稳定，为35 m（1σ）左右。

表6 双站跟踪模式下定轨精度统计Table 6 Statistics of orbital accuracy using double stations tracking data

需要指出的是，上述分析考虑的各类测量误差包括系统误差和随机误差，其中系统误差为常值偏差，随机误差为白噪声，为正态分布。实际跟踪试验中，由于跟踪设备周围环境的变化，VLBI 测量射电源标校误差，传播介质延迟修正不精确等，跟踪获取的测量数据的误差并非严格意义上的上述仿真采用的误差设置，因此实测数据的处理精度会较仿真精度有一定降低。

4 结 论

“鹊桥”位于地月L2 平动点的Halo 轨道运行，解算稳定的轨道需要长时间的跟踪数据，而高精度轨道则必须依赖USB/UXB 与VLBI 数据的联合使用。深空站具备同时开展测距、测速以及时延、时延率跟踪的能力。双站联测条件下，深空站可以同时获取测距、测速以及VLBI测量数据。本文就双站联测模式进行了仿真分析，得出如下结论。

1）每个深空站可以对“鹊桥”进行7～16 h的跟踪。若考虑双站共视约束，每天仍可进行5～12 h 的连续跟踪。

2）利用双站单天跟踪数据进行定轨，当跟踪弧段小于6 h时，可以不进行系统差解算；当跟踪弧长大于6 h时，系统差的解算更有利于轨道精度提升。

3）双站跟踪模式下，当跟踪时长超过2 天时，建议在轨道解算的同时估计动力学参数，该条件下，动力学模型的误差已经成为影响轨道精度的重要因素。使用长于3天的双站联测数据，有望实现优于百米的定轨精度。