同步优化失效概率与建设成本的天然气管网布局流程

安金钰 刘 鹏 安建博

贵州大学土木工程学院

0 引言

天然气长输管网的优化设计通常需要考虑4个方面的内容：气量和气压、气质安全、可靠性（保证事故时的气量）和经济性[1-5]。管网规划设计阶段一般以初选的管网布局为前提，以管网的建设费和管理运行费为目标函数，将满足压力和流量的能量方程作为约束条件，应用各种智能算法求解管径和水头损失[6-10]。随着全球环保力度的加大，管网的运行费不仅包括管网的管理费用，运行期间由于各种失效导致的风险损失费用也越来越不容忽视[11-12]。风险损失费用通常只针对已建管网进行分析计算，以期减少管网运行阶段所造成的不必要损失，如人员伤亡、建筑物破坏和环境污染等。由于风险存在的主要原因是管网所处地理位置及其周边环境，地理位置的确定取决于管网布局的设计，因而在管网布局规划阶段就应考虑失效造成的风险损失[13]。

目前管网布局优化仅仅以路径最短或建设成本最小[14-16]为目标函数，几乎没有在规划阶段考虑失效概率[17]的布局优化方法。虽然张圣柱曾讨论过这一问题[18]，但解决问题的思路与应用动态规划所得到的结论都有可能不符合工程实际。为此，笔者提出了一种可在管网布局规划阶段实现失效概率和建设成本同步优化的布局优化流程，并通过实例验证了其实用性和高效性。

1 失效概率的BP神经网络预测模型

利用案例中所经过区域已建成某管网中的60条管道的失效概率对BP神经网络预测模型进行训练和评价，其失效概率是通过故障树模型计算得到的。由于管道失效概率与引起失效的各基本事件因素有关，且为非线性函数，对于求解这种非线性函数，BP神经网络是一种高效的求解算法。失效概率的基本事件通常包括92个，训练的预测模型简化了输入变量，使其变量仅为电阻率、含水率、pH值和自然电位（-V）4个土壤成分值，以便提高管网布局规划阶段的效率。预测模型的训练和评价是基于Matlab R2015b建立。通过BP神经网络预测模型建立失效概率与土壤成分的关系，具体的模型建立步骤如图1所示。

图1 BP神经网络预测模型建立步骤图

1.1 创建神经网络

60条管道的土壤成分数据和失效概率值保存在failure_data.mat文件夹中，该文件包含2个变量矩阵：Soil为40行4列的土壤成分数据，Probability为40行失效概率数据。为了保证普遍性，采用随机法产生训练集和测试集，即可随机产生45个样品训练集和15个测试集。由于产生训练集（测试集）的随机性，每次运行所得结果均略有不同。

1.2 性能评价

通过计算预测值和真实值的偏差情况，可对网络的泛化能力进行评价。选用的2个评价指标为相对误差（Ei）和决定系数（R），其计算公式如下：式中表示第i条管道的预测值；yi(1,2,…,n)表示第i条管道的真实值；n表示管道数；l表示神经元隐含层数目。

相对误差越小，表明模型的性能越好。决定系数的范围在[0,1]内，越接近1，表明模型的性能越好；反之，越接近0，表明模型的性能越差。通过程序计算可知，BP预测模型的相对误差为5.24×10-4，决定系数为0.957 94。

某次运行结果如图2所示。结果表明此BP神经网络预测模型的失效概率预测结果与应用故障树计算方法所得的失效概率值很接近，从而证明所建立的BP神经网络模型能较好地实现失效概率的预测。

2 同步优化布局流程

基于管网的初始布局及对其预测所得的待优化管网失效概率，应用所提出的管网布局优化流程可获得失效概率和建设成本同步优化的管网布局。具体的优化流程如图3所示。

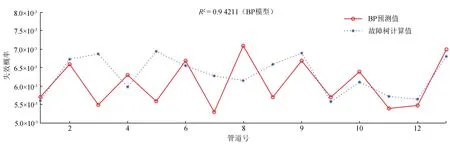
图2 测试集失效概率预测结果图

1）基于相近区域或类似区域已建管网的失效概率数据，训练BP神经网络，详见前文所述。

2）通过地理信息系统（GPS）或设置测试点获取1）中管网和待优化管网的土壤成分数据。

3）基于1）和2）获取的基础数据和已训练好的BP神经网络预测待优化管网的失效概率。

4）根据管网初始敷设路径所经过的区域确定其建设成本。

5）对失效概率和建设成本分别进行归一化，以便对两者进行综合。

6）失效概率和建设成本归一化后，其两者的乘积为得分。

7）将得分作为管网的边权值，利用最小生成树算法得出最优布局。

8）将得分最小的优化布局与最短路径、失效概率最小布局和建设成本最小布局进行对比分析，最终依据决策者和项目的侧重方向确定最优布局。

图3 管网优化布局流程图

2.1 建设成本

天然气长输管网的建设成本主要取决于材料费，其中钢材价格比例最大。为便于分析计算，基于2016年4月管材X80的钢材价格（6 800 元/t）确定管道经过不同区域时所需的建设成本。假定所用的管道均为同一管径，即单位长度建设成本只与经过的区域类型有关，此假设对笔者提出的布局优化问题不会产生任何影响。由于不同地区同一区域内管道的建设成本存在差异，所以选取的是某一地区的建设成本，具体建设成本如表1所示。

确定管道建设成本后，分别对管道建设成本和失效概率进行归一化处理，应用极差的标准化处理公式，即

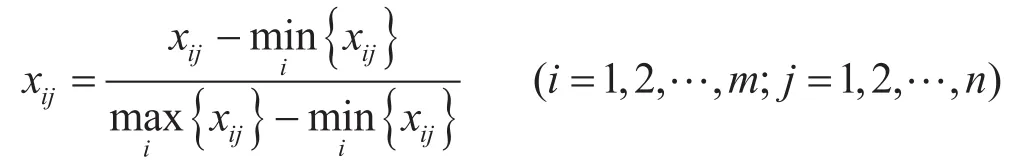
式中xij表示每条管道的建设成本或失效概率；i和j分别表示管道的节点号。

经过极差标准化处理后所得的新数据xij'，其极大值为1，极小值为0，其余的数值均在0与1之间。

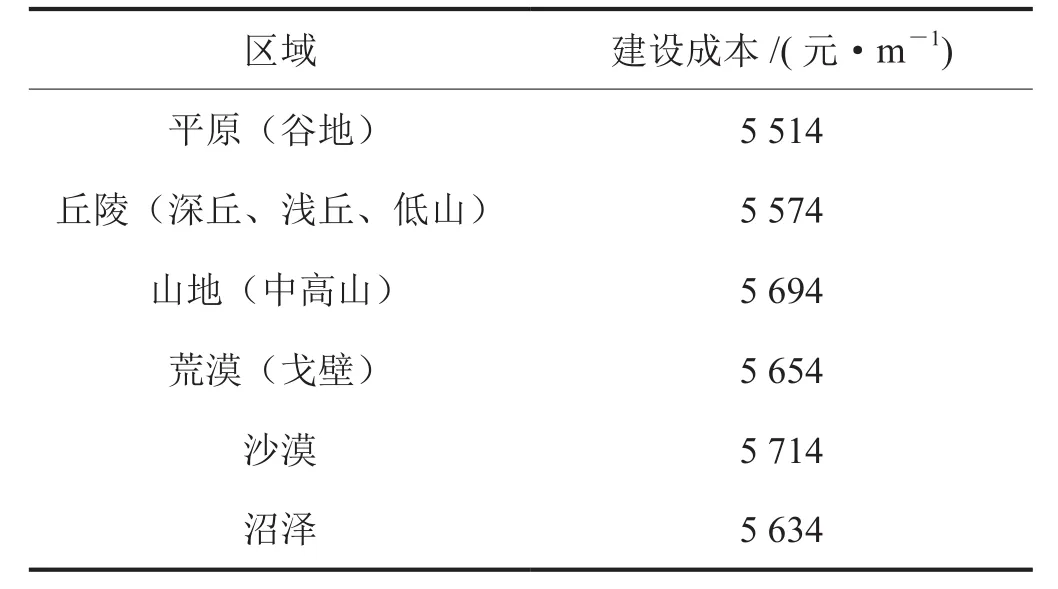
表1 天然气长输管道经过不同区域的建设成本表

2.2 最小生成树算法

运用动态规划求解所得的优化路线不一定符合实际，因为网格内可能包括建筑物或特殊地形障碍物，若求解的优化路线的坐标刚好处在某地下建筑物或其他无法敷设的区域，则所得的优化路线无法在实际中实施。最小生成树算法应用的前提是基于待优化管网已勘察确定可行的管网敷设路径。因此所得的优化布局相对于运用智能优化算法获得的优化布局更为准确[19]。

3 案例分析

以某油气长输管道为应用实例，管网的基础数据（土壤成分和管长）如表2所示，其初始敷设路线如图4所示。

基于预测的失效概率和管网的建设成本，将两者归一化后所得数值分别作为边权值，应用最小生成数算法，可得失效概率最小和建设成本最小的优化布局，此案例失效概率最小的优化布局如图5所示。另外，将长度和两者归一化后所得数值的乘积作为边权值，可得失效概率和建设成本同步优化的管网布局，即得分最小的优化布局图（图6），其建设成本最小和最短路径的优化布局与得分最小的优化布局相同。此案例得分最小的优化布局其建设成本最小，失效概率却并非最小，但也是最为接近最小失效概率的管网布局。因而此案例所得到的得分最小布局尽管未能实现失效概率和建设成本同步最小，但可以实现同步最优。

表2 管网的基础数据表

图4 管网初始可敷设路线图

图5 失效概率最小的管网优化布局图

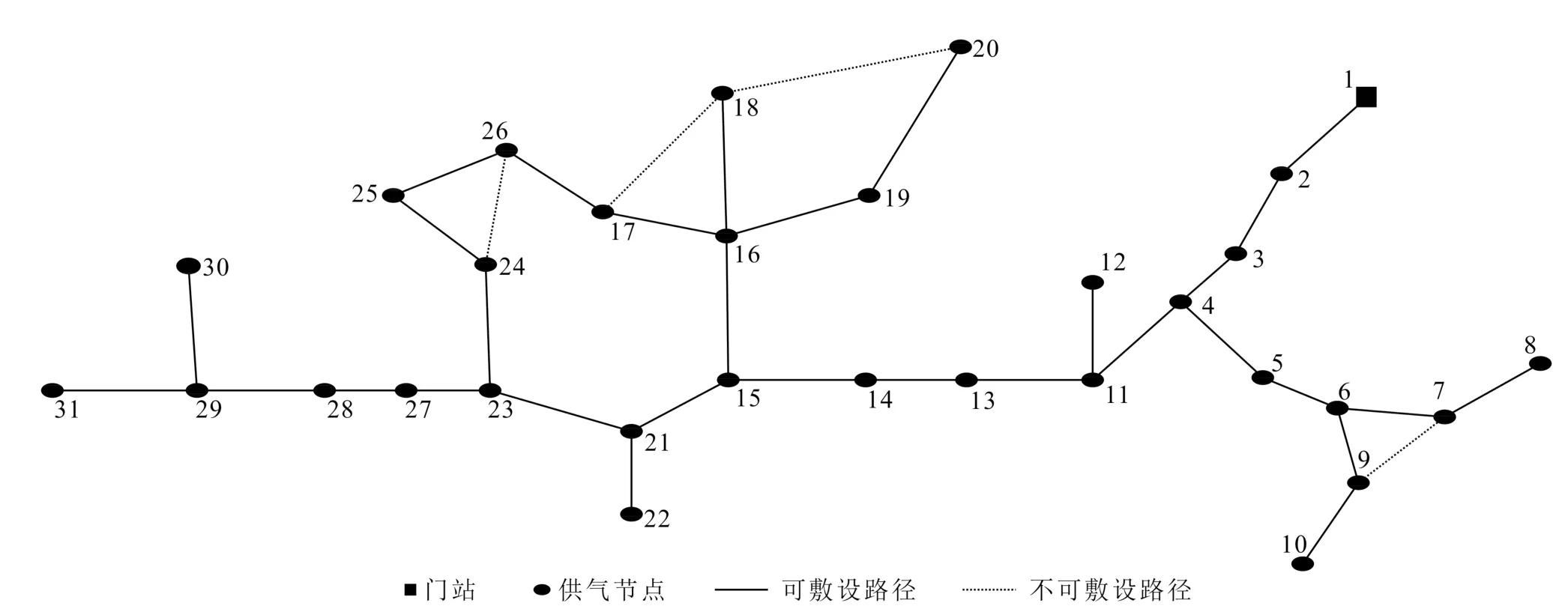
图6 得分最小的管网优化布局图

笔者尝试将其应用于另一案例，结果显示得分最小优化布局的失效概率为最小失效概率，建设成本最接近最短路径的最小建设成本，其优化布局与建设成本最小和管长最小的优化布局均不同，但与最小失效概率的布局相同，且管长最小和建设成本最小两者的优化布局相同。因此，得分最小的优化布局可以实现使失效概率和建设成本在管网规划布局阶段实现同步优化的目的。上述4种优化布局的最短路径、失效概率、建设成本和得分的汇总结果如表3所示。表3中所得结果均为归一化后的无量纲数值，便于进行对比分析。

由上述案例的优化布局图和归一化数值表可知：得分最小、建设成本最小和路径最短的3种优化布局结果可能相同（图6），失效概率最小的优化布局如图5所示，案例中得分最小的优化布局的失效概率和建设成本两者虽然不能同时达到最小，但可以使其中的一个因素达到最小，另外一个因素最接近最小，以使最终的优化布局实现失效概率和建设成本的同步最优。

表3 两案例4种优化布局的失效概率和建设成本归一化数值表

4 结论

1）传统的最短路径布局仅仅能实现建设成本费用最少的目的，并不能使失效概率最小。

2）提出的布局优化流程可在管网建设布局规划初期将失效概率及其建设成本进行综合分析。若所敷设的管网经过城区、重要交通要道、工业园区、人口密集地区或是某些特殊敏感地段，由于失效造成的损失巨大或是根据决策者的需求可选用失效概率最小的优化布局，相反，若所敷设的管网经过的地区人口稀疏，失效造成的损失可以接受，则可侧重考虑建设成本，选取建设成本即路径最短的优化布局。

3）所采用的建设成本可根据建设管网所处的地区及其建设年限进行对应调整，使其建设成本更加符合实际工程，另外对应的用于训练神经网络的失效概率既可通过故障树分析获取也可通过其他风险评价技术获取，均会对优化流程及其优化结果起到优化的效果。