孔喉结构对致密气微尺度渗流特征的影响

张烈辉 刘香禺 赵玉龙 周 源 单保超

1.“ 油气藏地质及开发工程”国家重点实验室•西南石油大学 2. 中国石油西南油气田公司勘探开发研究院3. 煤燃烧国家重点实验室•华中科技大学

0 引言

目前，对于致密气藏的渗流机理通常根据低渗透气藏的开发理论或实验方法来加以模拟和研究，但传统的数值模拟方法和宏观实验手段无法捕捉气体在致密储层中的微尺度流动特征；同时，微纳米级孔喉是致密储层储集和运移流体的主要空间与通道，而关于孔喉结构对致密气微尺度渗流特征影响的研究却较少。为了克服宏观方法的局限性，采用介观尺度的格子Boltzmann方法（LBM）对致密气的微观渗流进行模拟，进而研究孔喉结构对渗流特征的影响，不失为一种有效的方法。由于格子Boltzmann方法具有介观特性且并行性好，在致密砂岩气、页岩气和煤层气等非常规天然气的微尺度渗流机理研究中得到了应用。吴子森等[1]结合四参数随机生长法，采用LBGK-D2Q9模型研究了致密气的微尺度效应。王华龙等[2]考虑气体在多孔介质中的微尺度效应，将多孔介质等效为相互平行的圆柱体，将单通道LBM模型拓展并应用到孔隙群里气体渗流的数值模拟，为LBM深入研究气体在多孔介质中的渗流问题奠定了基础。任岚等[3]、姚军等[4]采用LBGK-D2Q9模型对页岩气藏微纳米孔隙中甲烷气体的流动进行了模拟研究，得到了不同温度、压力和孔道直径对页岩气微尺度流动的影响规律。张烈辉等[5]基于表征体元尺度的LBM模型，考虑滑脱效应，对页岩气在储层中的流动进行了数值模拟研究，研究结果表明页岩气在有机质中的流速略大于无机质中的流速。Fathi等[6]采用LBM模拟了二维Poiseuille流动，对Klinkenberg滑移理论进行了修正，并提出了双重滑脱模型。现有的文献报道通常针对平直管道或随机生成的多孔介质展开研究，未能体现出孔喉结构差异对气体微尺度渗流的影响。为此，笔者从致密气藏实际的温度、压力及储层孔喉特征尺寸出发，研究致密气的流态及采用LBM模拟致密气流动的合理性，然后考虑微尺度效应、滑脱效应等因素的影响，基于LBGK-D2Q9模型建立了致密气流动模型，进而针对平直通道开展流动模拟计算，将模拟结果与解析解、数值解的计算结果进行对比以验证模型的正确性，在此基础上，研究了孔喉结构对致密气微尺度渗流特征的影响。

1 致密气流动特征

Nelson[7]指出致密砂岩储层孔喉直径介于30～2 000 nm；邹才能等[8]、杨智等[9]通过大量实验数据总结出致密砂岩储层孔喉直径介于40～700 nm。在微纳米尺度，克努森数（Kn）是气体流动的特征参数，定义为分子平均自由程与流动通道特征长度的比值[10]，即

式中λ表示分子平均自由程，m；H表示流动通道特征长度，m。

分子平均自由程的计算式[11]为：

式中m表示分子质量，kg，考虑致密气为单组分甲烷，取值为2.658×10-26kg；ρg表示气体密度，kg/m3，本文采用美国国家标准与技术研究院（National Institute of Standards and Technology，简称为NIST）化学数据库中数据；d表示分子直径，m，取值为0.414×10-9m。

根据Kn可以将气体流态划分为以下4种：连续流、滑脱流、过渡流和分子自由流[12]。当流态为连续流和滑脱流时，流体流动均遵循Navier-Stokes方程，其中流态为滑脱流时需要对边界进行滑移修正处理；流态为过渡流时，连续介质假设不再成立，相应的基于该假设的传统计算流体力学方法（CFD）无法模拟对应尺度下流体的流动；对于分子自由流，通常需要采用分子动力学方法（MD）进行模拟。

为明确致密气在地层条件下的流态，绘制了不同温度（293.15 K、373.15 K）、压力（介于1～70 MPa）和储层孔喉直径（30 nm、1 000 nm、2 000 nm）下致密气的Kn变化曲线（图1）。从图1可以看出，当压力大于3 MPa时，Kn均小于10-1，气体流态为滑脱流和弱连续流，出现过渡流的概率较低。由于LBM是求解Navier-Stokes方程组的一种特殊离散方法。因此，采用LBM模拟致密气的微尺度流动是可行的。

图1 致密气流态划分图版

2 微尺度流动模型的建立

2.1 物理模型

常见的喉道类型概括为以下4种：孔隙的缩小部分、可变断面的收缩部分、片状或弯片状喉道及管束状喉道[13]。为了便于研究孔喉结构对致密气流动的影响，对物理模型进行如下简化，考虑孔隙为二维平直通道，将喉道抽象为规则方形凸起，如图2所示。

图2 孔喉结构简化示意图

2.2 格子Boltzmann模型

1992年，Qian等[14]提出了格子Boltzmann方法的基本模型——DdQm模型，得到了广泛应用。在模拟单相单组分的二维流动时，通常采用九速离散的LBGK-D2Q9模型（图3）。不考虑外加作用力时，LBGK-D2Q9模型的演化方程如式（3）所示。在LBM中所有物理量的单位为格子空间单位，均无量纲。

图3 描述致密气微观流动的格子Boltzmann模型示意图

式中f表示粒子分布函数；下标i表示离散速度方向，i=0,1,…,8； 表示格子空间中某位置；表示不同离散速度方向格子速度；δt表示格子空间时间步长；t表示格子空间时间；τ表示无因次松弛时间；上标eq表示平衡态。

在LBGK-D2Q9模型中，平衡态分布函数表示为：

其中

式中ρ表示格子空间宏观密度；wi表示权重系数；c表示格子速度； 表示格子空间宏观速度；cs表示格子声速；δx表示格子空间中的网格间距，一般其取值与δt数值相等，此时c=1。

格子空间宏观密度ρ和宏观速度 分别表示为：

对于LBGK-D2Q9模型，格子速度 和权重系数wi分别取值为：

在格子Boltzmann模型中，运动黏度作如下处理可使得模型在计算时具有二阶精度[15]，即

式中 表示格子空间运动黏度。

同时，对于单组分单相流体，格子空间中压力p与密度、格子声速的关系式为：

2.3 边界条件

对于微尺度流动问题，边界条件起着极为重要的作用。与宏观模拟方法不同，在LBM中边界条件设置的对象为分布函数。对微尺度通道入口和出口采用Guo等[16]提出的非平衡外推格式，上下壁面采用反弹与镜面反射组合格式（BSR）[17]以实现对滑移边界条件的处理。

对于二维平直通道内流动（图3），气体在进出口压差作用下，沿x轴正方向流动。以左侧x=0位置处网格节点为例，在迁移步后未知的分布函数为f1、f5、f8，采用非平衡外推格式，其边界处分布函数可以表示为平衡态和非平衡态两部分之和，即

式中上标neq表示非平衡态；下标i=1,5,8。

对于压力驱动的微尺度流动，进口位置处压力已知，而速度未知。在非平衡外推格式中，未知的平衡态分布函数采用入口处压力以及相邻节点的速度进行求解，即

对于非平衡态部分，使用相邻流体节点处的非平衡态分布函数近似处理，即

为了实现对壁面滑移的模拟，上下壁面采用BSR边界条件处理格式。由于采用Half-Way类型的反弹格式可使粒子运动图像清晰，计算精度高于标准反弹格式[10]。因此采用Half-Way类型的BSR边界条件处理格式。以下边界为例，迁移步后未知的分布函数为f2、f5、f6，此时可得

前人的研究中组合系数r多为定值[1,18-19]，但是根据Guo等[20]的研究结论，为消除数值离散效应，组合系数r应遵循如下选取规则，即

式中A1、A2分别表示与气固相互作用有关的系数；N表示网格数。

Guo等[21]在广义二阶滑移边界条件中给出A1、A2的计算式为：

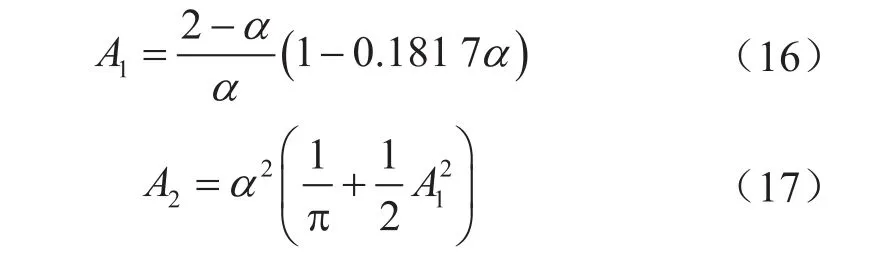
式中α表示切向动量调节系数，一般取值为1[4,22]。

显然，组合系数r不仅依赖于气体与壁面之间的相互作用系数A1、A2，也与Kn和网格数相关。

2.4 无因次松弛时间的选取

无因次松弛时间τ与Kn之间的关系确定是LBM模拟气体微尺度流动的一个基本问题，其中Kn是流动特征控制参数，τ与Kn之间的关系式[10]为：

实际上，气体在微纳米尺度空间中流动时还受到Knudsen层的影响。由于固体壁面的存在使得靠近壁面的气体分子平均自由程被截断，表现出不同于远离壁面的气体分子的运动特征，受到影响的这部分气体层则称为Knudsen层。Knudsen层的存在使得其气体分子平均自由程减小，当流动通道的特征长度远大于Knudsen层厚度时，Knudsen层对流体流动的影响不明显；但随着流动通道孔径减小，Knudsen层的厚度与通道特征长度的比值增加，其对流体流动的影响增大，表现出了不同于在常规大尺度通道中流动的特征，即微尺度效应。当气体流态为滑脱流时，分子之间的碰撞概率仍大于分子与壁面碰撞的概率，但Knudsen层的存在使得气体在边界的流动出现滑脱现象[23]。本文采用Guo等[24]提出的方法，将Knudsen层的影响考虑为使整个流动区域的气体分子平均自由程减小，此时无因次松弛时间τ和Kn的关系式为：

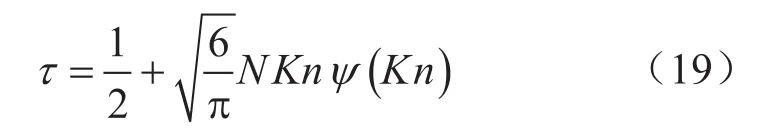
式中 表示平均分子自由程修正函数。

反映了孔隙壁面对气体分子运动过程的截断作用，其表达式为：

考虑到本文研究的微尺度渗流通道为变截面通道，流动通道的特征长度及Kn在不同位置会存在差异，因此式（19）中的网格数N和Kn均为局部参数。相应Kn根据下式进行计算，即

式中下标out代表通道出口中心位置。

3 模型验证

基于二维平板流动，假设入口处压力为pin，出口处压力为pout，将不同工况下本文模型的模拟结果分别与解析解及本文参考文献[25]中数值解的计算结果进行对比，以验证本文模型的正确性。

3.1 解析解验证

进出口压力分别设定为pin=1.01、pout=1.00，在运动黏度 分别取0.20、0.30的情况下，不考虑边界Knudsen层的影响，采用无滑移LBGK-D2Q9模型模拟流体流动。模拟中网格划分为Nx×Ny=300×100，计算得到出口处y方向的速度（Ux）剖面，并与解析解计算结果进行对比，结果显示两者具有很好的一致性（图4）。

图4 不同工况下本文模型数值解与解析解计算的速度剖面图

3.2 数值解验证

为进一步验证模型的正确性，采用本文模型模拟了Kn为0.019 4和0.194 0两种情况下出口处y方向的无因次速度剖面以及沿程无因次压力偏移量，并与本文参考文献[25]中采用DSMC、IP方法计算得到的结果进行对比。结果显示在不同Kn条件下，本文模型计算得到的出口处y方向的无因次速度剖面与DSMC、IP方法的计算结果吻合程度均较高（图5）；沿程无因次压力偏移量与采用DSMC、IP方法计算的结果虽存在少许差异，但整体趋势相符（图6）。

图5 不同Kn下DSMC、IP方法及本文模型计算的无因次速度剖面对比图

4 结果分析

图6 不同Kn下DSMC、IP方法及本文模型计算的沿程无因次压力偏移量结果对比图

在微尺度流动中，Kn是主控因素[22]，因此本文直接给定出口处Kn为0.019 4；采用压差驱动，定进口压力pin为1.1，出口压力pout为1.0，模拟时间步为100 000步以保证流动达到稳定状态。模拟计算中，网格数Nx为400、Ny为102，对直孔隙（对应孔喉比为5∶5）及孔喉比分别为5∶4、5∶3、5∶2和5∶1情况下的速度和压力分布以及相关参数进行分析。

4.1 Kn分布

由于沿程压力及孔喉比的变化，在不同位置处Kn的大小也存在差异。如图7所示，相比于沿程压力变化对Kn的影响，孔喉比的影响程度更大，在喉道处Kn将成倍增加；当孔喉比一定时，Kn沿喉道呈缓慢上升的趋势，且孔喉比越大，Kn上升的趋势越明显。

图7 不同孔喉比下沿程Kn分布图

4.2 压力分布

如图8所示，在孔喉比为5∶5时气体压力呈近线性分布；而存在喉道时，近线性压力分布规律被打破，气体在接近喉道进口处形成相对高压区，在离开喉道后形成相对低压区，且孔喉比越大，压力越低；在喉道位置处气体压力下降明显，在喉道两侧气体压力降低于喉道内，并且随着孔喉比的增加，喉道两侧气体压力变化越来越平缓。由于喉道的存在所导致的强非线性压力分布在一定程度上降低了气体流动动力，从而阻碍了气体的流动。

图8 不同孔喉比下孔道中心位置处压力沿程变化图

图9 不同孔喉比下喉道内压力降占比结果统计图

4.3 速度分布

如图10所示，当孔喉比大于1时，由于喉道结构的存在，气体流动的横截面积减小，导致喉道内外气体的流速存在明显差异，气体流速在喉道末端位置处出现最大值，这是遵循质量守恒定律的必然结果。如图11所示，在不同孔喉比下出口处y方向的速度分布剖面依然呈现为中间高、两边低的趋势，并且边界滑移速度随着孔喉比的增加而下降。总的来说，随着孔喉比增加，不同位置处的流速均较大程度地降低，从而导致流量降低。

图10 不同孔喉比下孔道中心位置处沿程速度变化曲线图

图11 不同孔喉比下出口处速度剖面图

5 结论

1）当压力介于3～70 MPa、温度介于293.15～373.15 K时，致密气藏中Kn小于0.1，气体流态为滑脱流和弱连续流，采用考虑微尺度效应和边界滑移效应的LBGK-D2Q9模型进行致密气流动的模拟是合理的。

2）本文模型的模拟结果与解析解及文献中DSMC、IP方法等数值解的计算结果吻合程度均较高，证实本文模型可靠。

3）流动通道的特征长度对Kn的影响远大于压力变化对其产生的影响，当孔喉比一定时，Kn沿喉道呈缓慢上升的趋势，且孔喉比越大，Kn上升的趋势越显著。

4）喉道的存在使得孔隙中压力的非线性分布特征显著，且压力降主要位于喉道内，同时孔喉比越大，喉道内的压降幅度越大。

5）压力的非线性分布使得气体的流动速度显著降低，从而降低了流动通道内气体的质量流量。