移动网格环境下的资源调度研究

摘 要：本文结合移动网格自身的特点，构建与其相适应的网络模型。同时，对资源决策过程中具体采用的调度优化算法进行研究，将基本微粒群算法进行离散化编码，在迭代的过程中引入变异算子以及遗传算子。经仿真，该算法不仅能提高微粒群整体向最优解逼进的速度，更可协助避免陷入局部收敛，对大规模求解的计算效果优越。

关键词：移动网格 资源调度 微粒群算法（PSO）

中图分类号：TN929.5文献标识码：A文章编号：1003-9082（2019）08-000-02

引言

目前，移动网格系统中重点会对移动设备进行通信接口和通信资源本身进行研究[1]。在移动网格中，用户与网络资源需要保持实时的、动态的连接，每个移动设备可看作为一个网格节点，又要解决它自身的缺陷：如频繁移动，带宽小，电池容量不足等问题。可见，如何高效地组织这些移动资源成为网格资源管理的关键问题之一。

一、移动网格的网络模型

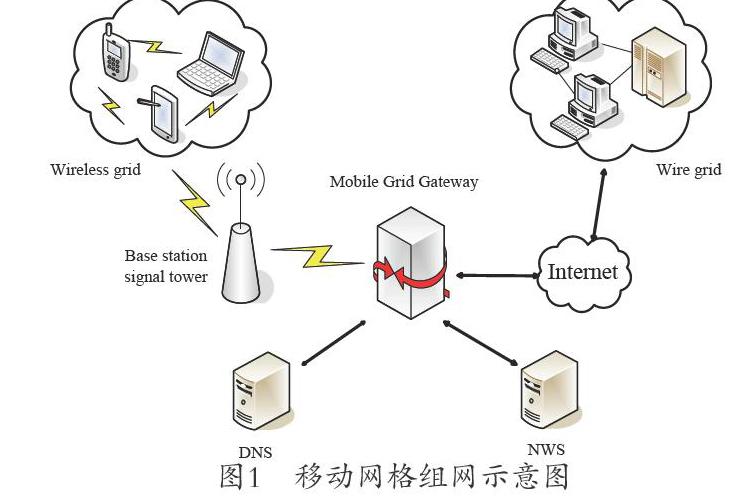
移动网格建立在有线网格的框架之上，由无线网格、网关、有线网格这三部分构成。其内部的资源管理服务机制是基于移动代理的分层模型，用移动资源代理实时地对资源进行监测和分配这样可增强系统的可扩展性，提高执行效率。

此外，在移动网格的网关中需要对资源代理执行监控，同时还要根据执行策略进行任务策略的选择，具体功能包括通信接口、信息采集、任务划分以及调度决策。信息采集作为关键的一个部分，用于收集和发布网格系统各节点的状态信息;NWS是一个分布式监控系统，主要用于实时跟踪网络资源和状况，提供网络性能预判功能。收集到的网格资源相关信息会定期反饋到调度决策模块，以供调度决策模块执行相应调度策略。

在移动网格运行的过程中，其中一个重要环节就是资源调度，具体地，根据系统吞吐量、资源利用率、用户需求等多种因素来选择最佳的任务分配方案。传统的资源调度常常只着重考虑任务在资源上的执行时间，而移动网格中更多的约束限制决定了其任务调度将更加复杂化，在选择调度算法时，要实时地从网格系统中监测最新的移动节点资源状况和位置变动等信息，更新路由表，把通信因素对性能的影响作为分析的重点。

二、移动网格资源调度算法

1.问题假定

在移动网格中，资源调度是把移动网格中提交的作业分割成许多子任务，根据子任务在不同移动节点上的执行的吞吐量和资源利用率不同，来选择最佳的作业分配方案，使任务完成时间最小。不同的作业调度算法可能拥有不同的调度目标，比如考虑服务质量优先、网络跨度优先、资源负载优先 [2]等，这里对移动网格中的资源调度问题作以下几个假定：

1.1同一时刻下，一台节点设备仅能执行一个任务，该任务不会被其他设备抢占。

1.2一个用户提交的任务被划分为许多任务，任务相互之间不具备必然的依赖关系，并且不会发生数据交互。

1.3实时获得未来一段时间内系统的预测信息，在资源节点故障或其所有者离开了网格系统的情况下，原来分配到该资源节点上的任务会被重新进行资源调度和分配。

资源调度采用以下数学模型进行搭建：

任务集合表示为，资源集合表示为，其中N小于等于M。获取资源和任务的属性信息矩阵：

任务在资源上的预期执行时间：

任务到资源上执行所需的通信时间、数据传输时间以及结果返回所用的时间之和，统称为通信时延：

寻求优化调度的目标就是求得这样一种映射方案，使总的时间损耗T最小，以获得最高效的系统性能。

2.基本微粒群算法

微粒群算法具有公认的诸多优点，比如计算简单、所需个体数目少等，尤其是在求解复杂问题时，其优越性表现地更为突显 [3-4]。其中，一个可行解可看作成“微粒”，每一个微粒会通过跟踪多个最优解来对自己进行更新，包括每个微粒自身寻找的个体最优解、种群整体当前寻找到的全局最优解。微粒采用以下方式来更新速度和位置：

3.改进的PSO资源调度算法

本文对PSO算法进行优化，改进的算法流程图如下所示：

3.1初始微粒种群，计算各微粒的适应度

设置基本参数，随机离散编码生成微粒群，每个微粒包含以下参数：

位置向量：，表示为把第个资源节点分配用为执行第个任务，的范围小于搜索空间N。

飞行速度：，表示第个任务下一次迭代所选择的资源节点与当前分配的资源节点之间存在的偏离，初始时的速度取值范围可以界于（-N+1）与（N-1）之间，并且取整。

适应值：将第个微粒当前的位置表示为，将微粒群中适应值最优的那个微粒所处的位置定义为，计算适应值。

以上参数按序存放用于表征一个微粒，主要是便于执行迭代和参数的更新，如下表所示：

假设初始化产生的微粒群的微粒数目表示为D，则微粒群可用二维数组表示，大小相应地就是D*（3*M+1），在迭代中不断更新该数组，慢慢逼进全局的最优解。

3.2采用遗传选择、随机交叉、线性衰减的惯性因子进行迭代

将适应度较低的部分微粒进入下一代，将其他适应度较大的微粒执行遗传选择以及随机的交叉，然后更新微粒：当交叉后微粒的适应度低于之前，则不改变原始位置，如果对之前更优，则对个人最优解进行更新。

此外，考虑到惯性因子具有以下特点：w值越大，越对局部最小点的跳出有利;w值越小，则可以加快算法进行收敛。为此，采用线性衰减的w进行改进：

（3）对微粒的速度、位移，不断更新个体最优解以及全局最优解

（4）判定收敛条件

设置迭代的总次数，达到此次数时算法终止，输出最优方案;否则重新回到步骤（2），继续执行迭代。

三、实验分析

采用该带有遗传因子和交叉因子的PSO算法与基本PSO算法进行比较进行仿真，模拟了在8个移动网格节点上来执行10-50个服务任务。设置初始种群为40，迭代次数为100，c1=c2=1.8，false=0.9， false=0.2。兩种算法下分配效率随任务数增加所产生的影响，如图所示：

由仿真图可以直观地发现，改进的PSO调度算法在任务数量变大的情况下调度效率更优越。分析其原因，任务数量越大，基本PSO算法容易陷入局部最优，使得向全局最优执行搜索的进度变得较慢。改进的算法则因为使用了遗传因子、随机交叉以及变化的惯性因子，会更加明显可以扩大搜索范围。此外，由于每一次迭代交叉具有随机性，任务调度的完成时间整体上具有随着任务量的增大而增加的趋势，但同时也呈现有一定幅度的波动。

结语

本文重点是分析了移动网格系统的特征，把传统网格资源调度模型应用其中。为了满足移动节点资源调度的复杂性，这里全面地考虑了影响分配方案的因素，然后采用改进的PSO算法来加快搜索的收敛速度，在更短的时间内获得更优的分配方案，在应对大规模移动网格中的动态资源管理问题上效果显著。

参考文献

[1]PHAN T，HUANG L，DULAN C. Challenge： integrating mobile wireless devices into the computational grid[C] //Proc of the 8thACM International Conference on Mobile Computing and Networking. New York ：ACM Press， 2002： 271-278.

[2]都志辉，陈渝，刘鹏.网格计算[M].北京：清华大学出版社，2002.

[3]Kennedy J，EberhartR C. Particle swarm optimization[C]//Proc. IEEE International Conference on Neural Networks.Pis-cataway，NJ，1995

[4]曾建潮，介婧，崔志华.微粒群算法[M].北京：科学出版社， 2004： 10-15.

作者简介;朱丹丹，（1987.5-）女，安徽省亳州市人，研究方向：通信与信息系统。