盾构掘进施工对既有基坑影响的理论分析

卢卓，魏焕卫

(山东建筑大学土木工程学院，山东济南250101)

0 引言

城市地铁区间施工方法以盾构法施工为主，盾构规划路线不可避免的邻近既有建筑结构，包括地下建筑、桩基、基坑、地下管廊管线等。盾构法施工会扰动土层，从而对周围环境产生影响，严重时会影响生活。针对盾构掘进对周围环境的影响这一课题，张琼方等[1]基于Mindlin解计算出盾构产生的附加应力，利用Winkler地基梁，进行叠加得到已建隧道总变形；王涛等[2]运用圆孔扩张—剪切理论，推导了盾构掘进中土体损失产生的附加应力；赵玉勃等[3]基于Mindlin应力解分析了在正面推力和盾壳摩阻力双重影响下附加应力的分布；武崇福等[4]推导了既有上部荷载下盾构正面推力，盾壳摩擦力和刀盘摩擦力的影响；张润峰等[5]推导计算了盾构的正面推力、盾壳摩阻力、土体损失对邻近桩基的附加应力影响；徐林[6]研究盾构隧道开挖对建筑物桩基的影响，分析不同影响因素对建筑物桩基础的影响变化规律。曾英俊[7]在实际工程的基础上分析盾构掘进对既有基坑的影响；殷榕鹏[8]考虑开挖过程挤土压力及摩擦软化效应影响，对既有隧道因新建隧道的施工所产生的的内力的影响进行研究。

文章基于盾构掘进施工实际工况，研究了盾构掘进施工产生的附加应力对邻近既有基坑的影响，利用Mindlin应力解[9]推导盾构正面推力和盾壳摩擦力产生作用在接触面上的附加应力；采用Sagaseta解[10]推导土体损失产生的附加应力，结合三者得到对基坑作用附加应力解答，并与工程实测数据进行对比。

1 盾构掘进附加应力的计算

1.1 盾构掘进对支护结构影响的力学模型及假定

盾构掘进过程是一个考虑时间、空间因素的过程，受扰动土体与盾构间的作用十分复杂。根据盾构掘进施工对周围土体影响的因素不同，可分为正面附加推力、盾壳侧摩阻力和土体损失3个主要因素作用产生的影响，如图1所示。为反映盾构掘进中主要因素对邻近既有基坑的附加应力的影响，作如下假定:

(1)假定土体为均匀各向同性的弹性半无限空间体，不考虑盾构和基坑开挖后边界条件的改变；

(2)假定正面推力为圆形均布荷载，盾壳摩阻力沿掘进方向分布，且分布均匀。

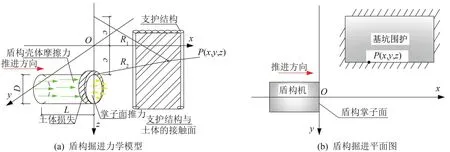
图1 盾构掘进示意图

1.2 掌子面推力、盾壳侧摩阻力土体损失的取值计算

1.2.1 掌子面附加推力fs的取值

赵玉勃等[3]和吴崇福等[4]仅将正面推力fs取为定值进行计算，不能完全表示对地层影响的盾构正面推力。王洪新[11]在挤土效应等的影响下提出刀盘附加接触应力求解公式，由式(1)表示为

式中:Δp′为开口的切入挤压力，kPa，取10～25 kPa；Eu为不排水弹性模量，kPa；ν为掘进速度，cm/min；w为刀盘转速，rad/min；k为闭口部分幅数，个；D为刀盘直径，m；ξ为刀盘开口率，%；μ为泊松比。

1.2.2 盾壳摩阻力fm的取值

赵玉勃等[3]和吴崇福等[4]将fm取为定值，但盾壳摩阻力依据地层土体等条件的不同摩擦力并不相同，朱合华等[12]在考虑自重和周围土体压力下进行简化，提出求解公式由式(2)表示为

式中:u为摩阻力系数；φ为土体的内摩擦角，°；γ为土体重度，kN/m3；c为盾构顶部埋深，m；W为盾构单位长度自重，kN/m；Pv、Ph分别为土体自重和侧向土压力，kPa；H为盾构轴线埋深，H=c+D/2，m。

砂和砂砾中的动态摩阻力系数取为0.3～0.4，而将黏土中的动态摩阻力系数取为0.2～0.3[13]。

1.2.3 土体损失Vloss的取值

盾构实际开挖面一般要比盾构机实际尺寸大，实际开挖面与盾壳间的间隙可以视为土体损失。土体损失计算模型有许多种，魏纲[14]在Lee等[15]提出的内切圆的模型基础上推导后，得到统一的土体损失模型，如图2所示，在这一模型基础上进行土体损失的计算。土体损失Vloss由式(3)表示为

式中:g=αGP+U3D+ω，其中GP为开挖面与盾构机间的几何空隙，m；α为空隙注浆折减系数，取值见文献[14] ；U3D为盾构前的土体三维弹塑性变形，假设土体为弹性半无限空间体，U3D=0；ω为施工因素，取值见文献[15] 。

图2 内切圆模型图

1.3 正面附加推力产生附加应力的计算

基于Mindlin应力解[9]，在盾构掘进正面推力的圆面上进行积分，求解得到正面推力fs引起支护结构与土体接触面上任一点P(x，y，z)的附加应力，如图1所示，垂直作用在支护结构上的附加应力σy1的解析解由式(4)表示为

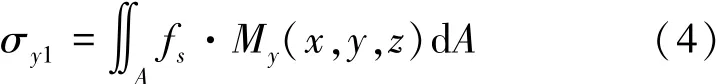
式中:My(x，y，z)为y向的应力影响系数；A为面积微元。

在Mindlin应力解中，应力可以表示为作用力与其应力影响系数My(x，y，z)乘积。My(x，y，z)由式(5)表示为

式中:c0为作用力点的埋深，m；x、y分别为所求点距作用点的x、y向间距，m；z为所求点的深度，m；R1、R2分别为计算点至力作用点的距离和计算点至力作用点沿xOy面对称点的距离，m，如图1所示，R1=

在盾构掌子面的圆域上运用数值积分的方法进行积分。依据实际积分条件，将直角坐标转换为极坐标，如图3所示。具体转换关系由式(6)表示为

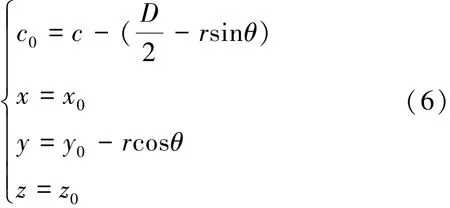
式中:x0、y0、z0分别为x、y、z坐标转换后的值；r为积分半径，m；θ为积分角。

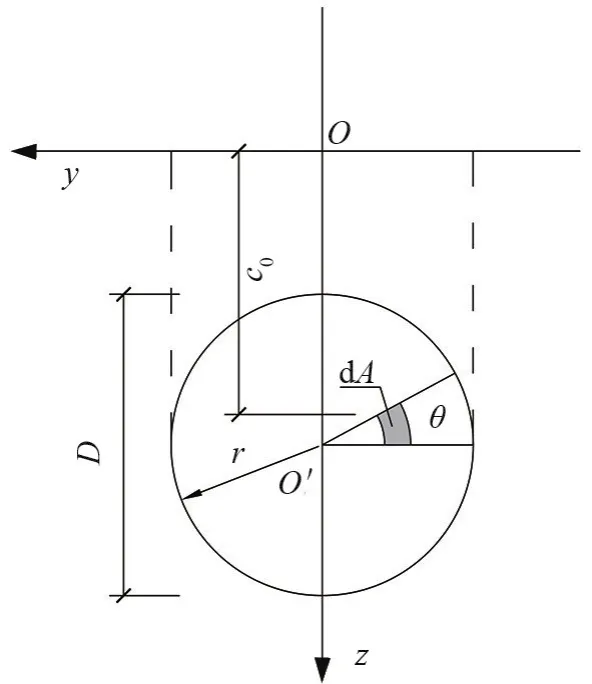
图3 圆面积分示意图

将坐标转化关系(6)带入式(4)中进行数值积分，得到式(7)为

式中:Fy1为掘进正面力作用在接触面上的附加荷载，kN/m，；σy1为作用在接触面上的附加应力，kPa；Aij为微元面积，m2；d为支护结构计算长度，m；k为划分份数。

利用式(7)可得到正面推力作用在支护结构上沿深度方向的附加线荷载。

1.4 盾壳侧摩阻力产生的附加应力的计算

基于Mindlin应力解[9]，在盾壳的侧摩阻力的圆柱侧面上进行积分，求得盾壳侧摩阻力fm引起支护结构与土体接触面上任一点P(x，y，z)的附加应力，如图4所示。垂直作用在支护结构上的附加应力σy2的解析解由式(8)表示为

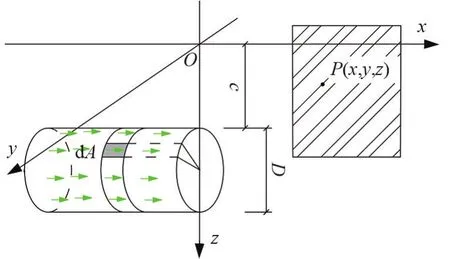
图4 盾壳积分示意图

同样，采用数值积分的方式进行积分。依据实际情况对坐标系进行转化，如图4所示。转化关系由式(9)表示为

将坐标轴转化关系(9)带入式(4)中进行数值积分，得到式(10)为

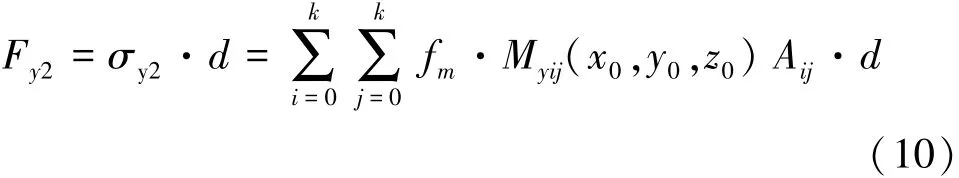
式中:Fy2为盾壳摩阻力fm作用在接触面的附加荷载，kN/m；σy2为作用在接触面上的附加应力，kPa。

利用式(10)可得到盾壳摩阻力fm作用在支护结构上沿深度方向附加线荷载。

1.5 土体损失产生的附加应力的计算

张润峰等[5]为避免镜像法的复杂，在 Pinto等[16]推导盾构土体损失引起地层位移解的基础上，利用弹性力学公式求解盾构施工土体损失对桩基础产生的附加应力解析解。

通过Sagaseta等[10]推导的某点产生的土体损失为基础，推导求解适用于作用在接触面上的点P(x，y，z)的三向解析解，如图5所示。

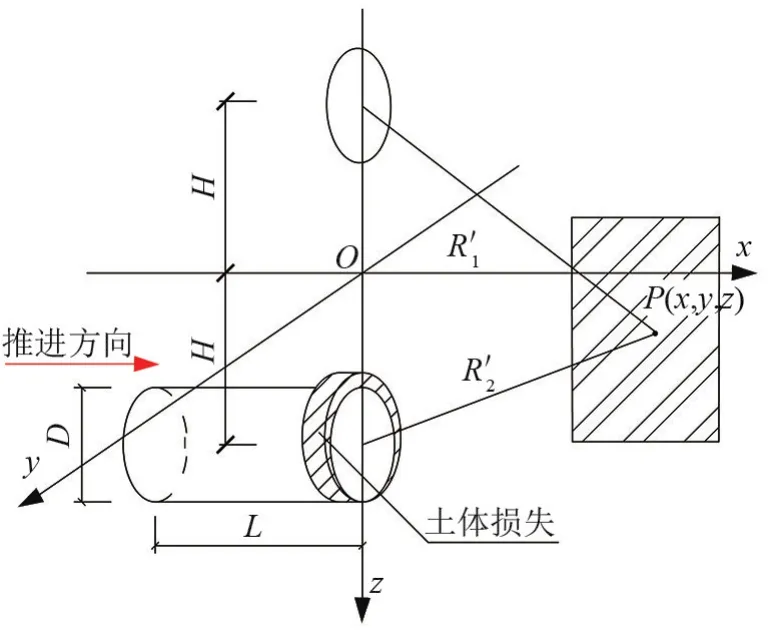
图5 土体损失示意图

计算点P的位移分量由时式(11)表示为

式中:sx、sy、sz分别为计算点P的x、y、z向的位移分量，m；R′1、R′2分别为计算点至力作用点的距离和计算点至力作用点沿xOy面对称点的距离，m。R′1、R′2由式(12)表示为

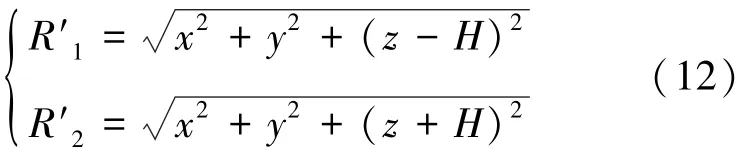
对计算的三向变形sx、sy、sz进行微分，带入广义胡克定律并沿盾构积分得到式(13)为

式中:Fy3为土体损失作用在接触面上的附加应力，kN/m；G为剪切模量，MPa；E为弹性模量，MPa；d为土体与支护结构的接触面上的计算长度，m；σy3为作用在接触面上的附加应力，kPa。

利用式(13)可得到土体损失作用在支护结构上沿深度方向的附加线荷载。

2 盾构掘进施工附加应力对既有基坑影响分析

基坑支护结构与单桩或桩基[5-6，17]不同，桩基是土中的基础构件，土中x、y、z三向附加荷载都会使单桩产生位移，而基坑支护主要受垂直于基坑内部的荷载(即y方向的荷载)的影响，而x、z方向荷载影响不大。当盾构在支护结构一侧施工时，只考虑y方向的附加荷载Fy对支护结构的影响。作用于支护结构上的计算长度附加荷载Fy由式(14)表示为Fy=Fy1+Fy2+Fy3(14)

2.1 算例概况

张冬梅等[18]对黄浦江观光行人隧道出入口竖井基坑一侧盾构施工的监测数据进行了分析整理。盾构外径为6.2 m，盾构衬砌管片壁厚为0.35 m，管片纵向长度为1 m，机身长度为8 m，盾构隧道顶部标高距地表18.13 m，竖井基坑与规划盾构路线最近距离为3 m；端头井基坑开挖深度为22 m，当开挖到15.5 m时，因盾构的掘进而停止开挖；围护结构为地下连续墙墙厚为0.8 m，深为37 m。钢管支撑型号为X609，厚为11 mm；标准段、端头井分别设置六道、七道支撑；平面设置间距约为3 m，如图6所示。土体的物理学参数见表1。

图6 施工平面图/mm

表1 土体的物理力学参数表

根据实际工程确定相关计算参数的取值，盾构掘进的掘进速度为 0.35 cm/min，刀盘转速为0.2 rad/min，闭口部分幅数为 4，掌子面压力为388 kPa，侧摩阻力为57 kPa，泊松比为0.3，土层加权重度为18.4 kN/m2，加权内粘聚力为11.33 kPa，加权摩擦角为23°。利用推导的解析解进行计算分析并与实测数据进行对比。

2.2 盾构掘进对既有基坑附加应力影响分析

2.2.1 支护结构的附加应力实测对比分析

取深度-20 m进行计算和比较。盾构掘进所产生的作用在支护结构上的附加荷载与实测土压力进行比较，如图7所示。图7中nD为支护结构接触面计算点与掌子面x方向水平距离，如图1所示。

沿盾构掘进方向，当x＞0时，实测数据与计算数值相比差别较小，随盾构的掘进，作用在支护结构上的附加荷载增加，数值计算在x=0.25D时，达到最大值，随之开始减小；实测数据在盾构恰好经过时，达到最大值。0＜x＜0.5D时，实测数据与计算数值的附加应力具有差异，这是由于进行数值计算时，Mindlin应力解和Sagaseta解均假设土体为线弹性体，而实际土体为非线弹性体，与实际情况差别较大，土体受盾构正面推力产生的挤压作用和侧摩阻力产生的剪切作用，导致土体发生变形。上海黄浦江地区以软土为主，在盾构掘进产生的附加应力的扰动影响下，只能恢复少部分弹性部分的变形。

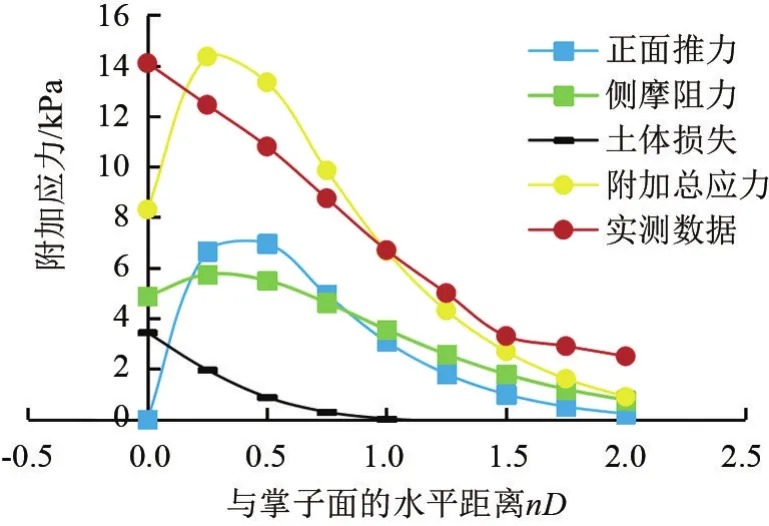
图7 土压力对比图

x＞1.0D时，fm＞fs，fm为支护结构的主要影响因素；0.25D＜x＜0.75D时，fs＞fm，fs为支护结构的主要影响因素，fm与fs的大小都随水平距离的减小而增加，fm初始值＞fs初始值，但fm增加速度比fs慢，靠近掌子面位置fs＞fm。土体损失产生的附加应力自1.0D开始增加，随距离的减小而增大。x=0时位于掌子面位置，土体损失产生的附加应力为3.2 kPa，对支护结构的影响发挥次要作用。附加总应力在2.0D处影响开始由0增加，到0.25D增加到最大值，由于0.25D后，fs减小到0，fm减小，总应力随之减小。

正面推力为圆面荷载，对土体以挤压作用为主，x=0时，附加应力为0，随距离的增加先增加后减小；摩阻力为盾壳圆柱面荷载，对土体以剪切作用为主，产生的附加应力随距离的增大，先增加后减小；侧摩阻力与正面推力对土体的作用不同，从而附加荷载曲线不同。

计算值与实测数据进行比较，计算值的最大值出现在0到0.5D之间，实测数据的最大值出现在掌子面位置，数值上二者相差不大；沿掘进方向，在掌子面前计算结果与实测数据的附加应力最大值差别不大，可按照计算最大值进行验算。

2.2.2 正面推力与侧摩阻力产生的附加荷载

正面推力和侧摩擦力产生的附加应力，如图8所示。正面推力与侧摩擦力产生的附加应力最大值出现在盾构轴线 -21 m处，沿深度方向，向上下两侧逐渐减小。

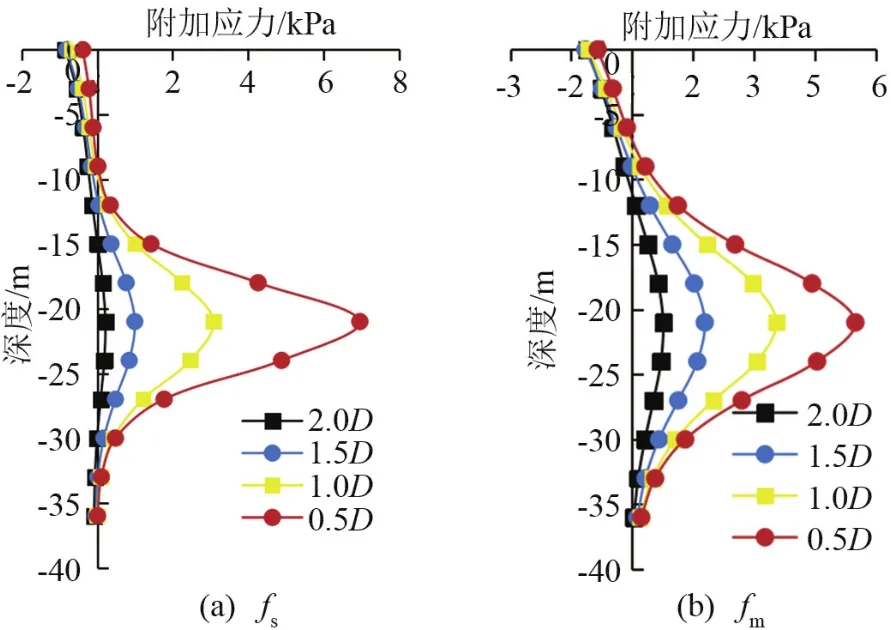
图8 正面推力和侧摩擦力附加应力图

正面推力产生的附加应力fs比侧摩阻力产生的附加应力fm减小速度要快；由2.0D到0.5D，fs变化幅度较大，fm变化幅度小；在0.5D处fs的最大值大于fm的最大值，此时fs对基坑支护结构的影响发挥主要作用，x＞1.0D时，fs的最大值小于fm的最大值，此时fm发挥主要作用。

2.2.3 土体损失产生的附加荷载

土体损失产生作用在支护结构上的附加荷载，如图9所示。土体损失产生的附加应力的最大值在盾构轴线位置-21 m处。x＜1.0D时，盾构掘进引起土体损失扰动，周围土体的附加应力开始增大，在盾构轴线深度处增加最为明显，附加应力值沿深度方向向上两侧减小，减小速度很快。与fs和fm在数值上相比较，数值较小不发挥主要作用。

图9 土体损失附加应力图

2.3 支护结构的变形增量分析

x=0.5D时，荷载增量较明显，按0.5D位置处计算支护结构的侧移增量。将计算结果与实测结果进行对比，如图10所示，计算结果比实测结果数值上要小，基坑在深度为15.5 m处暂停开挖，开挖完成部分设多道支撑，上部变形增量较小，随支护结构的深度增加，侧移增量先增加，后减小，支护结构底端变形增量减小为0。

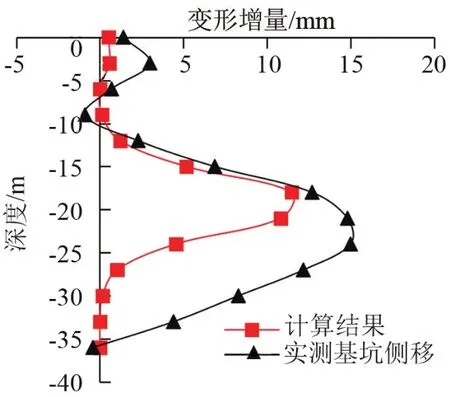
图10 侧移对比图

对比分析解析解计算结果与实测结果，发现二者的变化趋势规律相似。解析解计算结果在-18～-22 m某处达到最大值，此时盾构掘进产生的附加荷载最大，对支护结构的影响最明显，在 -25 m处地下连续墙的变形增量减小，并随深度增加趋近于0；实测结果中板桩墙的变形增量在 -25 m处达到最大值，后开始减小，在 -36 m处减小至0。基坑在深度-15.5 m处暂停开挖，开挖面以上设多道钢管支撑，可以有效限制地下连续墙的变形，从而15.5 m以上位置变形增量小；15.5 m以下盾构施工的附加荷载增大，过盾构轴线(-21 m)后附加荷载开始减小，支护结构的变形增量随盾构施工的附加荷载先增加后减小。

计算结果与实测数据规律相同，证明通过所推导的公式进行计算，可以反映盾构支护结构的侧移变化规律。

3 结论

基于Mindlin应力解，推导盾构正面推力和盾壳摩擦力产生作用在接触面上附加应力，并基于Sagaseta基本解推导了盾构掘进过程土体损失产生的附加应力，并通过实测数据与计算结果进行对比，得到如下结论:

(1)随盾构掘进靠近支护结构接触面计算点，支护结构所受的附加应力也在不断增大；当盾构不断远离计算位置时，附加应力在减小。沿盾构掘进方向公式求解计算的附加应力值与实测数据在掌子面前(x＞0)相似度较高，在盾构掘进掌子面距支护结构距离x=0.25D位置，支护结构受盾构掘进影响产生的附加应力较大，导致支护结构产生的挠曲变形增大，支护结构最危险、最不利。

(2)沿掘进方向，在掌子面前可按计算值进行计算，0.25D后附加应力开始减小，附加应力最大值与实测最大值差别不大，可按计算值附加应力最大值对支护结构进行验算。在实际工程中，支护结构受盾构掘进影响而产生的土压力以及变形量的变化较明显，应采取基坑停工，坑内堆土等方式保证基坑的安全。

(3)支护结构接触面计算点与与掌子面的水平间距x＞1.0D时，盾壳摩擦力产生的附加应力fm为支护结构的主要影响因素；计算位置与掌子面的水平间距0.25D＜x＜0.75D时，正面推力产生的附加应力fs为支护结构的主要影响因素；土体损失产生的附加应力自1.0D开始增加，＞1.0D时其值很小可以忽略不计，土体损失产生的附加应力对支护结构的影响发挥次要作用。