2019年高考数学命题①——仅以高考数学(理Ⅱ)卷为例谈论素养导向下的数学命题——可谓言之“既”预

李红庆 刘中维 郑月姣

(1.海南华侨中学 570206；2.湖北省天门中学 431700)

2019年6月7日下午5时，本年度高考数学考试结束.人们通过互联网浏览国家考试中心命制的几份高考数学试题，发现“中国高考命题正在实现从能力立意到素养导向的历史性转变.”[1]伏案桌前，面对本年度高考数学试题，重温文[1]，脑中迅速跳出如下观感：2019年高考数学命题，可谓言之“既”预.“考核目标从常规性的问题解决技能到创造性的探究能力；考查情境从学科知识化到真实情境化；试题条件从结构良好到结构不良；试题要素从单一因素到复合因素；”[1]……几份试题虽有个性，但共性都在于淋漓尽致地诠释文[1]的含义，为了鞭辟入里地谈论素养导向下的高考数学命题，本文仅以2019年普通高等学校招生全国统一考试理科数学(全国Ⅱ卷)[2]为例，讨论素养导向下的高考数学命题.

1 真实情境——由表及里 返璞归真

文[2]中第4、5、13、16、18题都以现代科学、现实生活和中华民族传统文化的真实情境为背景：无论是嫦娥四号探测器成功实现人类历史上首次月球背面软着陆的高科技重大成就，或是再常见不过的演讲原始评分规则、高铁经停正点率和乒乓球比赛规则的小事情，还是中国悠久的金石文化的代表之一印信中，呈现的南北朝时期的官员独孤信的印信形状问题，其实这些背景都是表面现象,命题的意图都是考查考生能否透过现象看本质,是否养成了“用数学的眼光观察现实世界,用数学思维分析现实世界,用数学语言表达现实世界.”[3]的好习惯，因此，考生必须返璞归真，回到数学的本质上思考问题，明确试题是在考查哪个数学的核心素养，以及怎样找到问题的切入点，才能披沙拣金.

案例1文[2]中第4题：2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆，我国航天事业取得又一重大成就.实现月球背面软着陆需要解决的一个关键技术问题是地面与探测器的通讯联系.为了解决这个问题，发射了嫦娥四号中继星“鹊桥”，鹊桥沿着围绕地月拉格朗日L2点的轨道运行，L2点是平衡点，位于地月连线的延长线上.设地球质量为M1，月球质量为M2，地月距离为R，L2点到月球的距离为r，根据牛顿运动定律和万有引力定律，r满足方程

案例2文[2]中第16题：中国有悠久的金石文化，印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多面体围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1.则该半正多面体共有个面，其棱长为________.

图1

图2

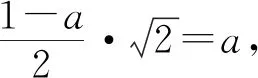
文[1]指出：“素养导向的高考命题注重情境化试题的考查.”，这对今后的课堂教学与考试评价起到很好的导向作用.情境活动是学科素养的载体，它包括现实的生活实践和学术探究情境活动.在课堂教学和平时的考试中，要有意识采用源于生活、社会的真实情境，考查和培养学生发现、提出、分析和解决实际情境中数学问题的能力，把单纯的解题教学转变为注重培养学生的科学态度和科学方法，养成用数学方法思考并解决实际情境问题的数学思维习惯，“将做题转变为做人、做事.”[1]，联系社会，唤起学生的责任担当意识与敢于创新的民族精神.

2 理性思维——交相辉映 相得益彰

素养导向注重对理性思维的考查，“要求学生以严谨的理性思维、严肃的科学态度去思考每一个实际问题.”[1]，文[2]中第12、20、22、23题就是针对科学思维考查设置的经典试题.“科学的理性思维是对客观的事物本质的属性以及潜在的规律和相互之间的关系的一种认知方式，这种方式必须建立在实际的事实之上去构建相应的模型，从而理解抽象化的概念，”[1]，这样题目的设计意图就是培养学生的科学思维能力，并通过逻辑思维推理和基本活动经验来养成创新思维习惯和品质.

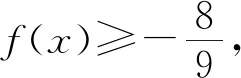
图3

案例4文[2]第22题：在极坐标系中，O为极点，点M(ρ0,θ0)(ρ0>0)在曲线C：ρ=4sinθ上，直线l过点A(4,0)且与OM垂直，垂足为P.

(2)当M在C上运动且P在线段OM上时，求点P轨迹的极坐标方程.

图4

设l上任一点Q的极坐标为(ρ,θ)，

由于|OQ|cos∠QOP=|OA|cosθ0=|OP|，

即得l的极坐标方程是

(2)设动点P(ρ,θ)，则|OP|=|OA|cosθ，

即ρ=4cosθ，

又点P在线段OM上，则0≤ρ≤ρ0，

即得点P轨迹的极坐标方程为

素养导向的高考数学试题命题，需要凭借试题这个载体来考查数学学科的核心素养，上述两例中都通过函数图象和方程图象的直观想象来确定函数的单调性和极角θ的取值范围，除了直观外，理性思维还体现在求动点轨迹方程常用的思维习惯和轨迹的完备性与纯粹性，求参量取值范围的充分性与必要性.

3 科学探究—— 传承创新 包容开放

“素养导向的高考命题注重科学探究能力的考查.研究开发探究型、开放型试题，发挥各种题型的组合功能，拓展考生思维空间.”[1]，文[2]中第21题基于传统常规思维与创新思维结合，也兼顾了探究能力的包容与开放，可以按常规思维的思路选择设直线QP或QG的方程为主线的常规思维的探究方式，也可以用创新思维拓展思路，选择设直线PG的方程为主线创新思维的探究方式，还可以同时兼顾常规思维与创新思维，设直线QP和PG的方程，同时从两条主线展开探究，当然这类问题的探究，也可以按逆向思维方式选择数学方法，把演绎推理转化为分析法、同一法或反证法：先假设PQ⊥PG′，由Q，E，G三点共线，推导出点G′和G是同一点.增加条件QP⊥PG不成立，推导出Q，E，G三点不共线.应该说，基于当前基础教育现状而言，这个试题的确是有一定的难度，准确说是有较高的灵活度，是近10年少有的考查科学探究与创新的好试题，下面简单介绍按创新思维主线探究几种解法的要点，统一设P(x1,y1)，Q(-x1,-y1)，E(x1,0)，G(x2,y2)，QG的中点为M(x0,y0) .

(1)求C的方程，并说明C是什么曲线;

(2)过坐标原点的直线交C于P，Q两点，点P在第一象限，PE⊥x轴，垂足为E，连结QE并延长交C于点G.

①证明：△PQG是直角三角形；②求△PQG的面积最大值.

主线1设直线QG的方程为x=my+x1，因点Q在其上，

即得直线QP的方程为2x-my=0，

即得kQP·kPG=-1，①问得证.

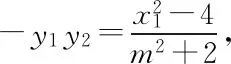
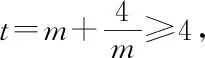
主线2设直线PG的方程为

y=vx+n(v<0)，

即得(2v2+1)x2+4vnx+2n2-4=0，

在②中，令kQP=k(k>0)，

当k∈(0,1)时，S′(k)>0，S(k)在(0,1)上递增；

当k∈(1,+∞)时，S′(k)<0，S(k)在(1,+∞)上递减，

主线3设直线QP为y=kx，直线PG为y-kx1=v(x-x1)，

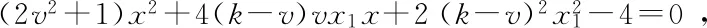
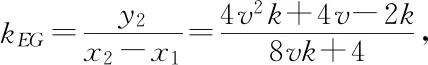
因为v≠k，所以kv=-1，即①问得证.

其实按此主线探究，设kPG=v，kQP=k，

直线OM的方程为y=vx，

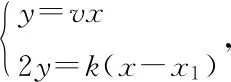
依题意，k>0，即得kv=-1.

由相似三角形性质，得

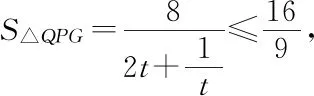
主线4设直线QP的方程为y=kx，

直线PG′的方程为x=-ky+x1+k2x1，

其中直线PG′与C相交于P，G′两点，G′(x′2,y′2)，

=0，

直线QG的方程为2y=k(x-x1)，

依韦达定理，得

所以x′2=x2，y′2=y2，点G′与G是同一点，即①问得证.

以上简单列举了几种创新探究方法和数学思想探究方法，按上述列举的切入的主线，还可以产生更多的科学探究成果.此题设计为优秀学生的科学探究提供了广阔的思维空间，可谓“海阔凭鱼跃，天高任鸟飞”， 突显了探究性试题的传承创新、包容开放的新景象.试题“从学生已有的知识结构出发，推陈出新，考查学生的创新能力与合作创新的学习意识.”[1]，这样的高考试题可以促成中学数学课堂中教师讲授为主的教学向主题研讨式学习的方向转向，纠正课堂教学中学生主体缺失的现象，找回围绕数学问题开展研讨性探究教学的自信，摈弃课堂逐题讲解和海量刷题训练的习惯，让课堂回归到教师主导引领下学生主动参与的研讨式学习上来.

结束语

恢复高考已经40余年了，从挑选精英的选拔考试逐步走向了大众化的“水平”考试，高考数学的命题环境也发生了很大变化，社会、考生家庭都寄予了很高的期望，也形成了很大的压力，特别是5G网络时代各公众号、社交群更是聚集了洪荒之力，命题者面临着巨大压力，面对着千万个望子成龙、望女成凤的考生家长，面对着“服务于” 基础教育的教育产业和培训机构的利益集团，命题者如履薄冰，稍不留神就会伤到千万个望子成龙、望女成凤的考生家长的愿望，动了利益集团的奶酪，引来了一片吐槽声,社会舆论还会有迅速走向民粹主义的可能，还有多少人能记住初心，能辩证理解试题的难与活，知道高考是选拔性的考试，它需要的是可靠的信度、效度，较好的区分度和灵活度，如果有一、两道试题稍微有一点难度和灵活性，就全盘否定命题者的辛劳付出与科学设计，那么科教兴国的梦想还能成真吗？作为教育工作者，需要理解与支持国家考试中心2019年命制的几份数学试题，用理性专业的眼光和辩证科学的态度，客观、公正地评价2019年高考数学试题，希望命题人继续在这条改革创新大路上坚定地走下去，并且把步子迈的更大一点，为国家出好题、把好关、选拔好人才.