关注价值导向 突出知识本质体现思维广度与深度 引导教学——2019年中考数学(北京卷)试题解析

王亮亮

(北京教育考试院 100083)

1 引言

2019年中考数学试卷延续了2015-2018年“稳中有变，变中求新”的特点，在全面考查基础知识的基础之上，扩大选材范围，突出对支撑学科体系重点知识的考查，关注价值导向，突出知识本质，体现思维广度与深度.以考查数学思维为核心，注重知识整体性与知识之间内在联系的考查，加强对数学知识形成与发展过程及灵活运用的考查.

试卷延续了“立德树人，引导教学，服务学生发展”的理念.试卷选材大气，将社会主义核心价值观和数学之美自然地融入试题中，让学生在解答过程中感受民族自豪感，体会数学之美.试题立意，以核心概念为抓手，以培养数学能力为目标，考查学生对知识本质的理解，从数学的角度思考问题和运用数学知识解决实际问题，让学生在数学的学习中有获得感，引导教学回归知识本质，关注数学思维，做到学以致用.试题设问方式易于学生入手，层次分明，适度综合，体现应用，让不同水平的学生都有充分发挥的空间.

2 试题解析

2.1 关注育人功能 体现积极导向

数学试卷选取合适的素材，将社会主义核心价值观自然融入到试题中，发挥试题的育人功能.如第21题，以国家创新指数排名为背景，着重考查学生读取、分析数据，获取信息的能力，让学生感受到我国的创新发展水平以及中国创新在世界中的位置.同时，让学生在数据分析与推断的过程中，了解党和国家提出“决胜全面建成小康社会”奋斗目标和“加快建设创新型国家”战略任务的意义，体现出了国家创新在国家经济发展中的重要地位.

2.2 关注四基要求 体现数学基础

《义务教育数学课程标准(2011版)》指出：“通过义务教育阶段的数学学习，学生能获得适应社会生活和进一步发展所必需的数学的基础知识、基本技能、基本思想、基本活动经验.”试题的命制注重对数与代数、图形与几何、统计与概率等基础知识的考查，在考查的过程中，突出对基础知识、基本技能、基本思想和基本活动经验的考查.

例1在矩形ABCD中，M，N，P，Q分别为边AB，BC，CD，DA上的点(不与端点重合).对于任意矩形ABCD，下面四个结论中，

①存在无数个四边形MNPQ是平行四边形；

②存在无数个四边形MNPQ是矩形；

③存在无数个四边形MNPQ是菱形；

④至少存在一个四边形MNPQ是正方形.

所有正确结论的序号是____.

解析此题考查特殊平行四边形(矩形、菱形和正方形)之间的关系.题目设计体现出了对知识掌握的整体性要求，不要把知识割裂开来看，而是从整体上看知识之间的联系性，这样才能深刻理解并掌握基础知识.

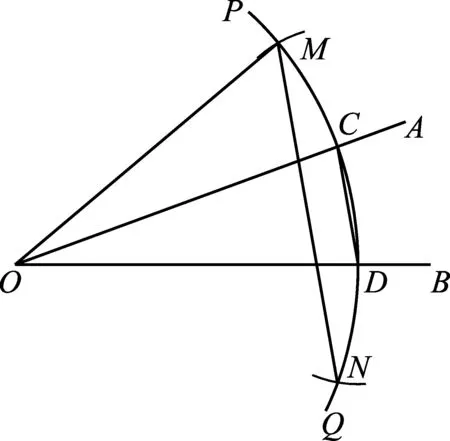
例2已知锐角∠AOB.如图，

(1)在射线OA上取一点C，以点O为圆心，OC长为半径作PQ，交射线OB于点D，连接CD；

(2)分别以点C，D为圆心，CD长为半径作弧，交PQ于点M，N；

(3)连接OM，MN.

根据以上作图过程及所作图形，下列结论中错误的是

(A)∠COM=∠COD;

(B)若OM=MN，则∠AOB=20°;

(C)MN∥CD;

(D)MN=3CD.

解析题目设计延续了2018年试题的特点，不仅要让学生掌握技能操作的程序和步骤，还要理解其中蕴含的数学原理，考查尺规作图中的逻辑推理.

2.3 关注教学过程 体现数学本质

数学教学的重要目标之一是让学生亲身经历数学知识形成、发展和应用的过程，积累数学活动经验，理解知识本质，感悟数学思想.今年数学试题的设计关注数学学习的完整过程，将学生日常学习活动经验浓缩于试题中，在学习过程中理解知识本质.

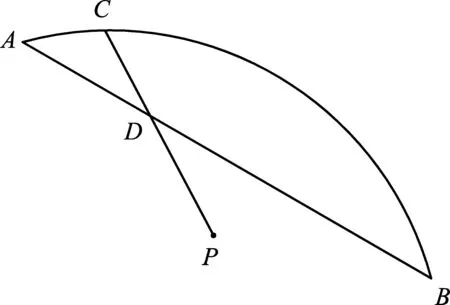
小腾根据学习函数的经验，对线段PC，PD，AD的长度之间的关系进行了探究.

下面是小腾的探究过程，请补充完整:

(1)对于点C在AB上的不同位置，画图、测量，得到了线段PC，PD，AD的长度的几组值，如下表：

位置1位置2位置3位置4位置5位置6位置7位置8PC/cm3.443.303.072.702.252.252.642.83PD/cm3.442.692.001.360.961.132.002.83AD/cm0.000.781.542.303.014.005.116.00

在PC，PD，AD的长度这三个量中，确定________的长度是自变量，________的长度和________的长度都是这个自变量的函数；

(2)在同一平面直角坐标系xOy中，画出(1)中所确定的函数的图象；

(3)结合函数图象，解决问题：当PC=2PD时，AD的长度约为________cm.

解析试题以函数学习的全过程为背景，考查函数概念，学生在研究几何图形中的各元素之间关系的过程中，首先根据动点C的不同位置，经历画图、测量、列表的过程，分析量与量之间的关系，判断自变量和因变量，确定函数关系；再经历描点和画函数图象的过程，探究变量之间的关系；最后利用建立的函数模型解决问题.引导教学关注积极地数学活动，关注知识本质，通过直观地操作活动和多层次地思维活动，从感性认识上升到理性认识，并加深理性认识.通过此试题的设置，在引导教学关注数学活动的基础上，引导教学更加关注函数的主线与本质.函数是研究运动与变化的数学模型，它来源于实际又服务于实际，紧密联系实际，从实际中抽象出函数的有关概念，又运用函数解决实际问题，这是贯穿于函数的主线.对于函数的本质要把握好两个实质：两个变量互相联系，对于自变量确定的每一个确定的值，对应的函数值都唯一确定.

2.4 关注思维品质 体现思维广度与深度

数学思维是学生数学素养的重要体现，试题通过对数学思维的广度与深度的考查，考查学生认识数学、理解数学、感悟数学的思维过程.

(1)依题意补全图1；

(2)求证：∠OMP=∠OPN；

(3)点M关于点H的对称点为Q，连接QP.写出一个OP的值，使得对于任意的点M总有ON=QP，并证明.

图1

备用图

解析本题主要从运动与变化的角度，结合函数图象，考查学生从特殊到一般、从直观到抽象、从感性到理性的思维过程.如第27题，第一次设计探究条件型问题，学生需要探寻问题成立的条件，考查学生在经历猜想、尝试等数学活动中，发现、提出问题，分析、解决问题.试题关注学生在解决一个综合性问题的过程中，既有操作、猜想发现和提出问题，又有演绎、证明分析和解决问题，考查学生的思维广度与深度.另外，该题取材于课本中的基本图形，通过从运动变化和图形变换的角度进行再设计，挖掘了教材中知识的内在联系，用综合的方法把知识串在一起，发挥了教材促进学生思维发展的功能，同时丰富的试题背景，提供给学生多角度思考问题的机会，提供给学生展示自我的舞台.试题难度设置适中，来源于教材，站位又高于教材，让老师思考题目与教材试题的相互关系.

2.5 关注实践能力 体现应用价值

现实生活中蕴含着大量与数量有关的问题，通过建立数学模型用数学的方法予以解决，体现了数学的应用价值.今年数学试卷扩大试题选材范围，加强与学生生活实际的联系，注重考查知识的运用和实践，考查了学生做事能力.

例5小云想用7天的时间背诵若干首诗词，背诵计划如下：

①将诗词分成4组，第i组有xi首，i=1，2，3，4；

②对于第i组诗词，第i天背诵第一遍，第(i+1)天背诵第二遍，第(i+3)天背诵第三遍，三遍后完成背诵，其它天无需背诵，i=1，2，3，4；

第1天第2天第3天第4天第5天第6天第7天第1组x1x1x1第2组x2x2x2第3组第4组x4x4x4

③每天最多背诵14首，最少背诵4首.

解答下列问题：

(1)填入x3补全上表；

(2)若x1=4，x2=3，x3=4，则x4的所有可能取值为________；

(3)7天后，小云背诵的诗词最多为________首.

解析试题以背诵诗词为背景，考查学生探求解决实际问题的最优方案的能力，体现学生运用所学知识分析解决实际问题的能力.

北京市中考数学学科的改革还在不断地进行探索与完善之中，文章若有不妥之处，请批评指正.