创设真实情境 突出学科特点 落实“五育”要求*——数学高考加强体美劳考查

任子朝 赵 轩

(教育部考试中心 100084)

1 问题的提出

在2018年9月的全国教育大会上， 习近平总书记提出要努力构建德智体美劳全面培养的教育体系，形成更高水平的人才培养体系.习近平总书记指出，“要树立健康第一的教育理念，开齐开足体育课，帮助学生在体育锻炼中享受乐趣、增强体质、健全人格、锤炼意志.要全面加强和改进学校美育，坚持以美育人、以文化人，提高学生审美和人文素养.要在学生中弘扬劳动精神，教育引导学生崇尚劳动、尊重劳动，懂得劳动最光荣、劳动最崇高、劳动最伟大、劳动最美丽的道理，长大后能够辛勤劳动、诚实劳动、创造性劳动.”[1]中共中央、国务院印发的《中国教育现代化2035》提出，增强综合素质，树立健康第一的教育理念，全面强化学校体育工作，全面加强和改进学校美育，弘扬劳动精神，强化实践动手能力、合作能力、创新能力的培养.[2]

构建德智体美劳全面培养的教育体系包括两个重要内容，一是构建教育大目标，二是构建教育大体系.全国教育大会已经勾勒出我国教育的大目标，而构建教育大体系则需要教育全方位的共同努力，包括教育各环节的运行方式、运行规则，各方面的相互关联、相互作用、相互协调的建制.构建全员育人、全程育人的教育体系，评价是教育体系的重要组成部分，学生评价是最终的落脚点，更关乎教育的出发点.习近平总书记指出，要深化教育体制改革，健全立德树人落实机制，扭转不科学的教育评价导向，从根本上解决教育评价指挥棒问题.[1]2019年高考数学科积极落实全教会的要求，加强体美劳方面的引导.明确考查目标，探索体现体美劳导向的试题的命制规律，创新考查形式，提高体美劳在评价中的比重，充分发挥评价的激励和指导功能，促进教育目标的实现.

2 明确体美劳的考查目标

在高考中融入体美劳要求的试题，主要是引导学生增强审美能力、培养健康意识和劳动观念，更多地是发挥考试的积极导向作用，引导学生去感悟、去体验，并不是直接地考查学生体美劳的发展水平，即考生的体育运动水平、艺术素养和劳动技能的高低.要将音、体、美、劳等课程通过试题素材融入考查过程，在发展学生智育的同时，加强对审美能力和修养、健康观念和意识、劳动精神和实践等方面的考查，唤醒学生对生活中真善美的认识、理解和尊重，引导教育教学破除“唯智”的不良倾向，夯实学生全面成长的基础，促进学生思想道德素养、科学文化素养、人文和审美素养、健康和劳动素养的全面提升.对体美劳的考查要掌握适度的原则，要遵循教育规律、学生的学习规律、认知成长规律和考试测量的规律.

3 发挥学科特点，落实体美劳的考查要求

将体美劳的要求融入高考试题，要贯穿试题素材的选取、情境的构造、问题的提出等试题设计的各个环节进行，要进一步明确数学学科在融合德智体美劳方面，特别是体美劳方面的结合点和结合的形式，创新题目形式，选准设问角度，明确考查要求，制定评价标准.

(1)彰显改革开放以来的建设成就，增强学生的民族自信心和自豪感.设置真实的问题情境，以体验式试题融入五育要求，以理性思维为主线考查解决问题能力.

高考要落实“立德树人”根本任务，要使数学试卷不仅成为选拔的有效手段，更成为育人的重要途径和载体.要把高考内容与国家经济社会发展、科学技术进步、生产生活实际、发展阶段特点紧密联系起来，通过考查学生灵活运用所学知识分析解决实际问题的能力，认识我国在社会主义建设中的成就，增强学生的民族自信心和自豪感.

例1(2019年Ⅱ卷理科第4题)

2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆，我国航天事业取得又一重大成就. 实现月球背面软着陆需要解决的一个关键技术问题是地面与探测器的通讯联系. 为解决这个问题，发射了嫦娥四号中继星“鹊桥”，鹊桥沿着围绕地月拉格朗日L2点的轨道运行.L2点是平衡点，位于地月连线的延长线上. 设地球质量为M1，月球质量为M2，地月距离为R，L2点到月球的距离为r，根据牛顿运动定律和万有引力定律，r满足方程：

例2(2019年Ⅱ卷文科第14题、理科第13题)

我国高铁发展迅速，技术先进.经统计，在经停某站的高铁列车中，有10个车次的正点率为0.97，有20个车次的正点率为0.98，有10个车次的正点率为0.99，则经停该站高铁列车所有车次的平均正点率的估计值为.

例2以国人为之骄傲的高铁列车为背景，设计一道蕴含基本统计思想的试题，考查考生对统计中用样本估计总体的思想的理解，以及对用样本数字特征估计总体数字特征的方法的掌握与运用.试题注重基础，计算量较小，在考查知识的同时能够激发学生的民族自豪感，爱国情怀，同时引导考生热爱数学，增强数学应用意识.

(2)提升学生的健康意识和审美意识，引导学生弘扬劳动精神.命制情境化试题，使考生置身其中，主动解决问题.在体育方面，首先要树立“健康第一”的教育理念，设置真实的体育比赛的场景，让学生在利用数学知识解决体育问题的过程中，体会体育的意义和价值，力图把学生吸引到体育场、健身房、大自然中去锻炼身体，强健体魄，让学生在体育锻炼中享受乐趣、增强体质、健全人格、锤炼意志.在美育方面，坚持以美育人、以文化人，通过试题展示现实世界中蕴含的数学美，提髙学生审美和人文素养.在劳育方面，要通过试题的情境设置，让学生真正懂得“劳动最光荣、最崇髙、最伟大、最美丽”的道理，通过体会劳动实践情境让他们去体验、去感悟.

例3(2019年Ⅰ卷理科第15题)

甲、乙两队进行篮球决赛，采取七场四胜制(当一队赢得四场胜利时，该队获胜，决赛结束).根据前期比赛成绩，甲队的主客场安排依次为“主主客客主客主”.设甲队主场取胜的概率为0.6，客场取胜的概率为0.5，且各场比赛结果相互独立，则甲队以4:1获胜的概率是.

例3以为篮球比赛的赛制为背景设计概率问题，考查随机事件概率的性质与计算.篮球运动是学生熟悉和热爱的体育运动，篮球比赛也是大家喜爱的体育竞技项目，比赛的规则是我国职业篮球联赛的实用规则，增强了试题的真实性、趣味性.体育比赛的结果具有不确定性，自然地就能够产生各种概率问题，这些问题既是学生熟悉的问题，也是学生感兴趣的问题.学生可通过所学的概率知识和方法得到答案，通过对本问题的解答，使学生感受概率的魅力和概率统计知识在实际问题中的应用.引导学生热爱篮球、热爱体育.

例4(2019年Ⅱ卷理科第18题)

11分制乒乓球比赛，每赢一球得1分，当某局打成10:10平后，每球交换发球权，先多得2分的一方获胜，该局比赛结束. 甲、乙两位同学进行单打比赛，假设甲发球时甲得分的概率为0.5，乙发球时甲得分的概率为0.4，各球的结果相互独立. 在某局双方10:10平后，甲先发球，两人又打了X个球该局比赛结束.

(1)求P(X=2)；

(2)求事件“X=4且甲获胜”的概率.

乒乓球堪称中国“国球”，中国运动员的乒乓球水平在世界范围内名列前茅，屡夺冠军.例4以乒乓球本身为背景，设计一个随机变量X，通过X的不同取值来表示不同事件，计算事件的概率.试题设计新颖，巧妙地将概率问题融入乒乓球比赛中，试题运算简单，重在对概率问题的分析与理解，在考查考生对概率知识掌握程度的同时，展现了概率的应用领域.对概率与统计知识的教育与教学具有很好的导向作用.试题背景是考生熟悉和引以自豪的乒乓球，会产生一种自然的亲切感和自豪感，激发学生参与体育运动的热情.

例5(2019年Ⅰ卷文、理科第4题)

A．165cm B．175cm C．185cm D．190cm

例5以古希腊著名雕塑断臂维纳斯为背景，以人体长度结构符合黄金分割比例为基本背景，设计了身高估算的问题.解答试题需要的基本知识和基本技能是考生熟悉的，试题背景贴近考生生活实际，解题思路多样，给广大考生提供了一次很好的几何审美的学习机会，提供了黄金分割比的研究机会，有助于激发学生学习数学的兴趣.同时也能使学生亲身体验到美、感受到美，是对美育引导的一次探索.

例6(2019年Ⅲ卷文、理科第16题)

学生到工厂劳动实践，利用3D打印技术制作模型.该模型为长方体ABCD-A1B1C1D1挖去四棱锥O-EFGH后所得的几何体，如图,其中O为长方体的中心，E，F，G，H分别为所在棱的中点，AB=BC=6cm，AA1=4cm.3D打印所用原料密度为0.9g/cm3.不考虑打印损耗，制作该模型所需原料的质量为g.

例6的设计源于实际的科学教育实践内容，以3D打印为背景，用学生熟悉的长方体和四棱锥作为基本模型，编制了一个计算空间几何体的体积以及计算模型所需原料质量的问题.3D打印是先编制程序，再利用3D打印机将材料直接打印成所设计的模型.近些年，3D打印发展方兴未艾，具有良好的应用前景.题目通过情境的创设，引导学生更多接触先进科学技术的前沿知识，在学科实践中学习科学技术，这样能激发学生学习的兴趣，开阔学生学习的视野，从而实现五育并举全面发展的教育目的.

(3)吸收中国优秀传统文化和科学发明、发现的素材，结合数学知识和原理编拟试题，体现古代劳动人民的智慧和成果.使学生认识到劳动创造人类、劳动创造世界、劳动创造美好生活的意义，树立劳动光荣、劳动致富的观点，培养热爱劳动的良好习惯，锻炼吃苦耐劳的精神，为人生发展奠定坚实的基础.

例7(2019年Ⅱ卷文、理科第16题)

中国有悠久的金石文化，印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1.则该半正多面体共有个面，其棱长为.

图1

图2

例7融入了中国悠久的金石文化，赋以几何体真实背景，有助于帮助考生对这个全新几何体进行认识.在这个问题的解决过程中，考生要借助几何体的对称性，不仅使学生感受到数学的对称美，更感受到这种美对于解决问题的真实力量.题目侧重于在真实情境下对知识的理解和应用，对中学立体几何的教学有积极的引导作用.

例8(2019年Ⅰ卷理科第6题)

我国古代典籍《周易》用“卦”描述万物的变化. 每一“重卦”由从下到上排列的6个爻组成，爻分为阳爻“——”和阴爻“- -”，右图就是一重卦. 在所有重卦中随机取一重卦，则该重卦恰有3个阳爻的概率是

例8是以我国古代典籍《周易》中的“重卦”为情境设计的简单古典概率计算问题，有利于考生运用所学的知识解决问题.试题考查了概率与计算，引导考生关注生活中的数学问题，增强数学的应用意识.同时试题内容引自我国经典的典籍，引导考生热爱我国传统文化，学习我国传统文化.通过本题的求解，使考生体会到概率的运用，以及体会到我国传统文化的博大精深.

(4)注意学科间的渗透和交叉，增加具有自然科学和社会人文学科背景的试题，促进学科间的融合以及核心素养的有效考查.加强实验操作和社会实践能力的考查和引导，培养学生的实践能力.

例9(2019年Ⅲ卷文、理科第17题)

为了解甲、乙两种离子在小鼠体内的残留程度，进行如下试验：将200只小鼠随机分成A，B两组，每组100只，其中A组小鼠给服甲离子溶液，B组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图：

甲离子残留百分比直方图

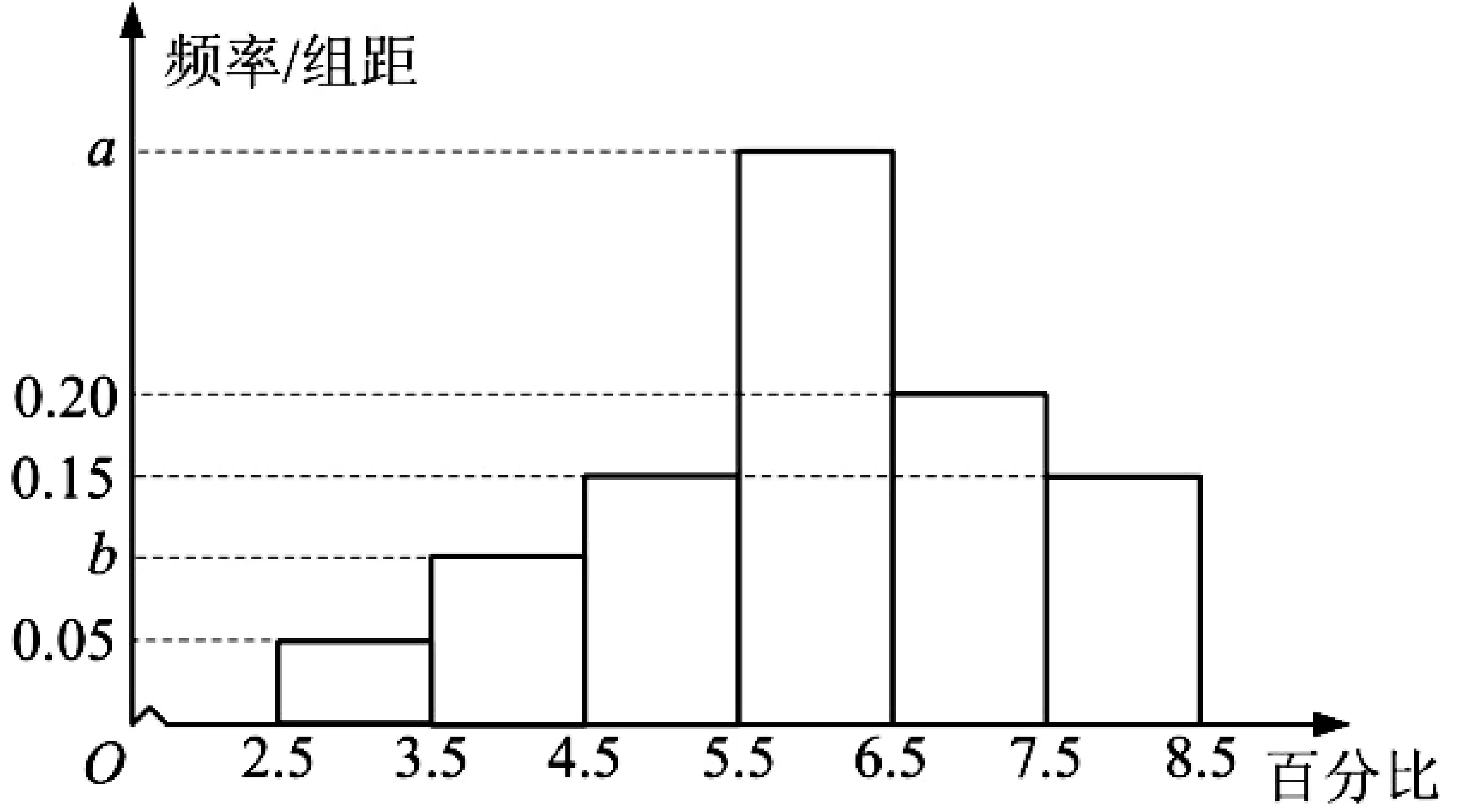
乙离子残留百分比直方图

记C为事件：“乙离子残留在体内的百分比不低于5.5”，根据直方图得到P(C)的估计值为0.70.

(1)求乙离子残留百分比直方图中a，b的值；

(2)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).

例9以考生熟悉的素材，编制了一个分析和处理数据的问题.为了了解甲、乙两种离子在人或动物体内的残留程度，以及评估残留程度的差异，需要安排实验并获得样本数据，然后分析数据并做出结论.试题着重于对实验数据的分析和处理上，考查的内容属于考试大纲的基本要求，设计的问题具有现实意义和统计意义，展示了统计学知识在生物实验中的具体应用.考生通过对试题的作答，可以体会到数据及数据处理的问题在学习生活中无处不在，进一步体会到数学与统计学在其他学科中的应用价值，有利于统计学的教学改革.

(5)体现数学在解决体美劳问题中的价值和作用.试题不是穿靴戴帽，不是生搬硬套，而是有一定的价值、一定的挑战性，学生必须经过深入思考才能解决问题.

高中数学中的许多知识内容与体美劳问题都具有紧密的联系，如三角函数，函数极值，概率与统计等.可以通过多种考查方式与展现形式将这些知识内容与相关的实际问题相结合，如应用函数工具描述运动规律；应用相关系数分析各种因素与运动成绩的相关性；应用排列、组合知识和方法安排比赛；应用概率、分布列、事件独立性、条件概率预测比赛获胜的概率；应用数学期望、方差分析运动员的运动成绩；应用函数极值计算材料最省、用料最少、效益最大问题；应用统计图表展示劳动生产率、劳动成果统计；应用一元线性回归模型预测社会、经济未来发展趋势；应用2×2列联表进行生产因素的独立性检验等.

(6)确保背景公平.在涉及体育的试题中，力图选取公众喜欢的项目和在我国比较普及的项目，避免冷僻的体育运动和规则复杂的项目.美育方面体现对美的表现和对美的欣赏，避免雕塑、绘画、作曲、演唱等专业的知识和特殊的技巧.对劳动观念的考查重在引导和教育，避免专门的劳动技能和复杂的劳动操作.

4 结语

高考是我国的基本教育制度，是立德树人落实机制的关键环节和重要组成部分.在高考中，德智体美劳五育之间，互为依托，互相影响，相辅相成，密不可分，五育共同服务于立德树人这个根本目标.实现五育并举不仅是基于培养社会主义建设者和接班人的需要，同时也更是培养健康美好的社会主义公民个体的需要.在高考命题中，要通过试题情境的设置、真实问题的提出、利用学科知识解决问题的过程，达到五育并举，助力德智体美劳全面发展目标实现.