滚塑烘箱内空气和模具温度分布均匀性的仿真研究

刘学军,江 辉

(1.北京工商大学材料与机械工程学院，北京 100048；2.温岭市旭日滚塑科技有限公司，浙江 温岭 317511)

0 前言

以往大部分对滚塑工艺加热阶段的理论研究的重点都是放在模具与其中的物料和空气混合物及熔融塑料之间的换热机理上，试图建立一个准确的数值仿真模型来模拟滚塑模具的壁面温度以及模具内部空气的温度[1-4]，从而为滚塑工艺过程的最优化控制提供理论依据。在这些研究里一般是将模具的外壁面设置为第三类热边界条件，给出烘箱内的温度以及烘箱内加热介质与模具的表面传热系数。这样处理所得的数值仿真区域不用包括模具以外的空间，因此也不用考虑滚塑烘箱的具体结构和模具在烘箱内的运动情况，从而简化了问题。

但上述传热模型无法研究某些实际的滚塑工艺问题。例如，在滚塑加热阶段经常会出现模具表面温度分布均匀性较差的情况，从而使得模具内某些地方的物料过热，某些地方的物料却又熔融不彻底，从而破坏了塑料制品的强度和表面品质[5]。由于滚塑烘箱内空气和模具表面的温度分布均匀性与烘箱和模具的结构大小、进气道的形状以及模具的运动情况等因素都有关系，因此需要建立一个与上述不同的传热模型来进行这方面的理论研究。

彭伟等[6]采用FLUENT软件对滚塑烘箱内的速度场和温度场进行了数值模拟，并根据计算结果对热气流的流入方向提出了改进方案以提高加热效率。但该文献在对计算结果的分析过程中更多的是关注模具周围热气流的温度分布的均匀性，而没有定量地研究模具表面温度分布的均匀性。刘学军[7]79通过数值仿真研究了滑梯形滚塑模具表面温度分布的均匀性与进风温度、速度以及进风口和回风口的周向位置间的关系。并采用温度的标准偏差来定量地表征模具表面温度分布的均匀性，温度标准偏差越小表明温度分布的均匀性越好。但在该文献的传热模型里，进风速度的方向总是与进风口垂直，这与实际情况有一定的差异。另外该文献也没有研究模具表面温度分布的均匀性与模具尺寸间的关系。为了更好地进行滚塑工艺过程的优化控制，在烘箱的进气道里一般还安装了可转动的叶片，称为调整叶片，可以像导流板一样用来改变进风的方向。关于叶片的转角对滚塑烘箱内空气和模具表面的温度分布均匀性的影响，迄今为止还未见任何文献有这方面的研究。

本文应用FLUENT软件通过数值仿真首先研究不同的叶片转角组合对滚塑烘箱内部空气的温度分布均匀性的影响，然后研究不同的叶片转角组合对滚塑模具的表面温度分布均匀性的影响，并定量地研究调整叶片转角对改善上述温度分布均匀性的有效程度。最后研究在某个特定的叶片转角组合情形下滚塑模具表面温度分布的均匀性随模具长度的变化规律。这些研究可为滚塑烘箱和模具的结构设计以及工艺参数的优化设置提供理论依据。

1 传热模型

如图1所示为滚塑烘箱、模具、叶片、进气道以及风机的横截面形状。该图还显示了烘箱进风口和回风口的位置。风机将被加热的高温空气通过进气道吹入烘箱内部区域以加热滚塑模具，通过调整安装在进气道里的叶片的转角可以改变进入烘箱里热空气的流动方向和模式。滚塑加热过程开始后，模具以12 r/min的均匀转速绕着烘箱的轴线逆时针转动。已知烘箱的内径为3.5 m、进风温度为350 ℃、进风速度为20 m/s并与水平方向成45 °夹角，烘箱内部空气和模具表面的初始温度均为27 ℃。

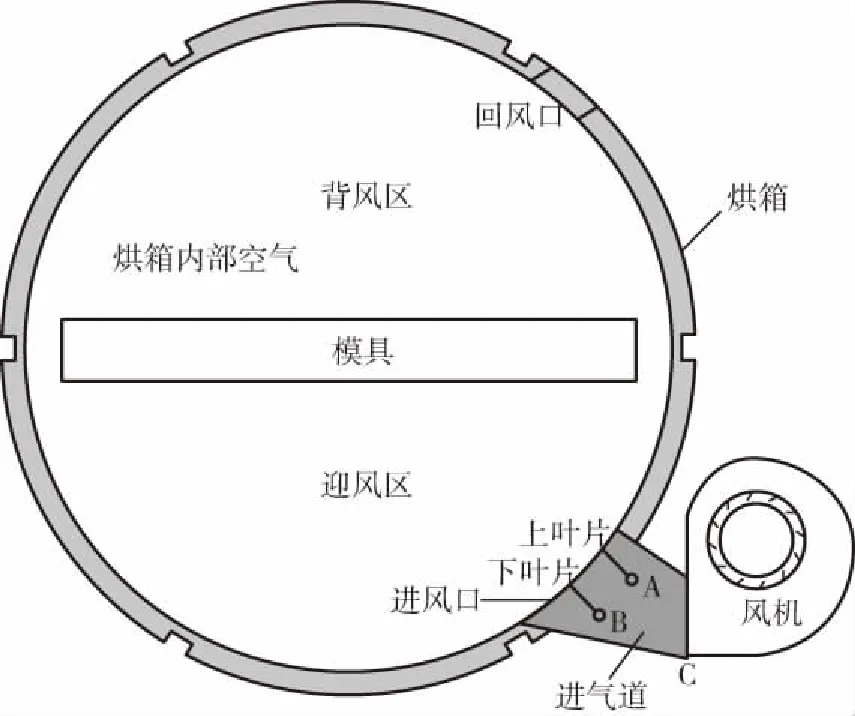
图1 滚塑烘箱、模具、叶片、进气道和风机的结构Fig.1 Structure of rotational molding oven, mould, vanes, inlet and fan

计算时长定为5 s，即模具在烘箱内完成绕轴线转动一周所花费的时间。虽然5 s的计算时长远远不能覆盖整个滚塑工艺的加热阶段，但本文的目的不是为了计算烘箱内空气和模具表面在滚塑加热过程中真实的温度标准偏差，而是为了比较在各个不同的叶片转角组合情形下烘箱内空气和模具的温度标准偏差的相对大小，从而获得最佳的叶片转角组合情形。因此只要在所有的叶片转角组合情形下，用来比较温度标准偏差的依据是一致的，即都是比较模具完整转过一周时的温度标准偏差，那么由仿真结果所得的最佳叶片转角组合就可以使烘箱内空气和模具表面的温度分布最均匀。

上、下叶片的横截面形状都是扁长的矩形，其纵向长度均为230 mm、厚度均为10 mm。上叶片转动中心A与进气道入口下端点C的水平间距为282 mm，与其竖直间距为408 mm；下叶片转动中心B与其水平间距为471 mm，与其竖直间距为225 mm。由于结构的限制，这2个叶片的转角只能在0 °～40 °的范围内，该转角是指叶片的纵向与水平方向间的夹角。

为简化计算，不考虑整个结构轴向尺寸的影响，即这是一个非稳态的二维不可压缩空气的流动与传热问题。本文将通过FLUENT软件采用k-ε两方程湍流模型[8]对其进行数值仿真。另外假设烘箱和进气道的内壁面以及模具和叶片的外表面都是绝热的。这个假设与实际情况间肯定是有差异的，但它只会影响表面温度标准偏差的绝对值大小，而不会影响在各个叶片转角组合情形下的温度标准偏差间相对比较的结果，即不会影响本文研究结论的准确性。

本文建立了2种传热理论模型—无模具模型和有模具模型。在无模具模型里，图1所示的模具是不存在的，通过改变上、下叶片的转角来分别计算在5 s时烘箱内部空气的温度标准偏差，从而得到最佳的叶片转角组合情形。其仿真区域为烘箱内部空气以及排除叶片外的进气道内部空气。无模具模型的核心思想是假设只要烘箱内部空气的温度分布比较均匀，就可以使得放置其中的模具表面的温度分布也比较均匀。这种模型的优点是计算简单，仿真计算量较小。在有模具模型里，需要考虑模具的形状大小和转动情况，通过改变上、下叶片的转角来分别计算在5 s时模具表面温度的标准偏差以获得最佳的叶片转角组合情形。其仿真区域为排除模具外的烘箱内部空气以及排除叶片外的进气道内部空气。由于在仿真计算过程中，模具是转动的，因此该仿真区域是随时间变化的。在该模型里，以模具为界把烘箱内部区域分成迎风区和背风区，迎风区就是正对进风口的模具表面与烘箱内壁面所形成的空气区域，而除此之外的烘箱内另一侧空气区域就是背风区。

为了衡量通过调整叶片转角来改善温度分布均匀性的有效程度有多大，本文定义了一个称为叶片调整有效率的指标，其计算公式如式(1)所示：

(1)

式中η——叶片调整有效率，%

Smin——在最佳叶片组合情形的温度标准偏差，即温度标准偏差的最小值，℃

S0——当叶片不存在时的温度标准偏差，℃

叶片调整有效率越大，说明调整叶片转角可以越显著地改善温度分布的均匀性。为得到叶片调整有效率，还要采用上述2种传热模型分别计算当进气道里没有安装叶片时烘箱内空气和模具表面在5 s时的温度标准偏差。关于温度标准偏差的定义公式详见文献[7]81。

2 数值计算结果及分析

2.1 采用无模具模型的仿真结果

图2分别表示了当上叶片的转角为0 °、10 °、20 °、30 °、40 °时，烘箱内部空气温度的标准偏差随下叶片转角的变化规律。可以看出，当上、下叶片的转角均为0 °时，温度标准偏差最小，即当上、下叶片都设置为水平方向时，烘箱内部空气的温度分布最均匀。而当上叶片转角为0 °且下叶片转角为40 °时，温度标准偏差最大，即此时烘箱内部空气的温度分布最不均匀。

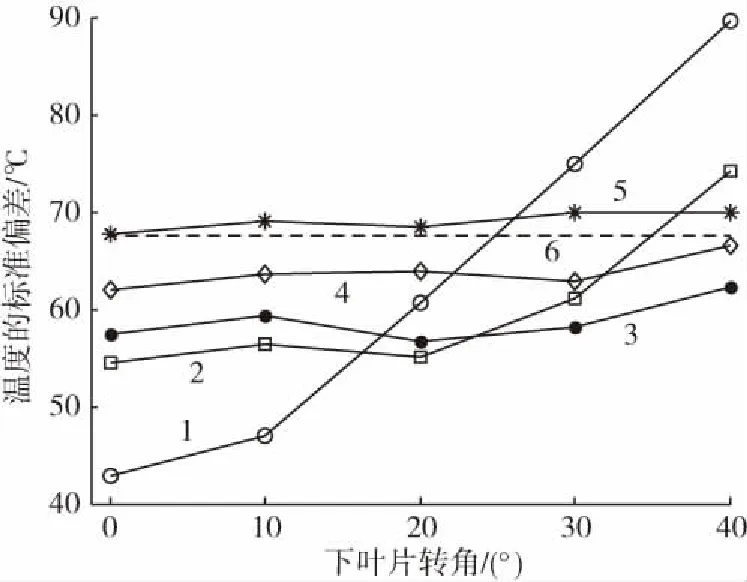
上叶片转角：1—0 ° 2—10 ° 3—20 °4—30 ° 5—40 ° 6—无叶片情形图2 烘箱内部空气温度的标准偏差随下叶片转角的变化曲线Fig.2 Variation of standard deviation of air temperature inside oven with the angle of lower vane

烘箱回风口处的空气压力低于烘箱内部的空气压力，因此回风口对烘箱内部的热空气具有一定的抽吸作用。当上叶片转角为0 °且下叶片转角为40 °时,上、下叶片之间形成了一个类似喷嘴一样的通道，将进气道内的热空气以高速沿斜上方向挤压进入烘箱内部。这股高速气流很容易被处于烘箱右上侧的回风口抽吸走，这种流动模式会将大部分的热空气都导引到烘箱右侧的较小区域里，从而造成在该区域里空气温度较高。而进入烘箱左侧的较大区域里的热空气比较少，造成在该区域里空气温度较低。因此整个烘箱内空气温度分布的均匀性就很差。当上、下叶片的转角都为0 °时，就可以利用这2个水平的叶片将进气道里的热空气尽可能多的向烘箱左侧区域导引，从而改善了烘箱内空气温度分布的均匀性。图3(a)和3(b)分别显示了上述2种情形在5 s时烘箱内部空气的温度分布。可以看出，在上、下叶片转角均为0 °的情形，烘箱左侧空气温度的最低值比上叶片转角为0 °且下叶片转角为40 °的情形要高得多，另外具有最低温度的空气分布范围也比该情形要小。

(a) 上叶片转角为0 °，下叶片转角为40 ° (b) 上、下叶片转角均为0 °图3 5 s时2种情形下烘箱内部空气的温度分布Fig.3 Temperature distribution of air inside oven in two cases when time is 5 s

另外值得注意的是随着上叶片转角的增大，烘箱内部空气温度的标准偏差随下叶片转角的变化曲线变得越来越平坦。当上叶片转角为40 °时，在0 °～40 °的范围内调整下叶片转角对改善烘箱内空气温度分布的均匀性几乎没有效果。这是因为当上叶片转角为40 °时，无论下叶片调整到该范围内的哪个角度，下叶片分别与进气道下壁面和上叶片之间形成的2个通道都不会对即将进入烘箱的热空气产生明显的挤压作用，因此对烘箱内部空气的流动状态影响较小，故几乎不会改变其温度标准偏差的大小。

图2中的虚线表示当进气道里没有安装调整叶片时，烘箱内部空气温度的标准偏差。可以看出在总共25种叶片转角组合情形中只有7种情形的内部空气温度标准偏差大于无叶片时的情形。根据式(1)可以计算出叶片调整有效率为36.5 %，这说明通过调整叶片的转角可以显著改善烘箱内部空气温度分布的均匀性。另外可以看出无叶片时烘箱内部空气温度的标准偏差与上叶片转角为40 °且下叶片转角为0 °的情形几乎相等，这说明在该叶片转角组合情形，叶片的存在对烘箱内部的空气流动状态几乎没有影响。

2.2 采用有模具模型的仿真结果

图4、图5分别给出了长度为2 m和3 m的模具，采用有模具模型计算所得的模具表面温度的标准偏差随叶片转角的变化规律。从图4可以看出，对于2 m长的模具，在上叶片转角为0 °且下叶片转角为20 °的情形，模具表面温度的标准偏差最小，即此时模具表面的温度分布最均匀。显然这与图2所示的最佳叶片转角组合情形是不一样的。这说明使得烘箱内部空气的温度分布最均匀一般不能使得模具表面的温度分布最均匀。虽然采用无模具模型得出的最佳叶片转角组合情形与采用有模具模型得出的结果有一定的偏差，但从图4也可以看出，即使按照前者的结果来设置上、下叶片的转角，所得的模具表面温度分布的均匀性也好过大部分的叶片转角组合情形。考虑到无模具模型的仿真计算量比有模具模型的小很多，因此无模具模型的仿真结果也有一定的参考价值，或者说无模具模型的计算方法也有一定的实际应用意义。

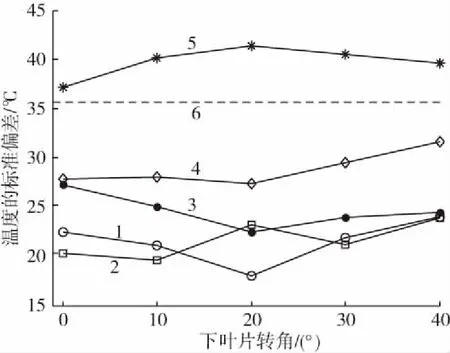
上叶片转角：1—0 ° 2—10 ° 3—20 ° 4—30 °5—40 ° 6—无叶片情形图4 2 m长模具表面温度的标准偏差随下叶片转角的变化Fig.4 Variation of standard deviation of temperature at 2 m long mould wall with the angle of lower vane

图4中的虚线表示当进气道里没有安装调整叶片时，2 m长模具表面温度的标准偏差。可以看出除了上叶片转角为40 °之外的其他转角组合情形，其模具表面温度的标准偏差都比无叶片情形的要小。按公式(1)计算所得的叶片调整有效率为50 %。这说明通过调整叶片的转角可以大大改善2 m长模具的表面温度分布的均匀性。另外可以看出无叶片时模具表面温度的标准偏差与上叶片转角为40 °且下叶片转角为0 °时的情形很接近，这说明在该叶片转角组合情形，叶片的存在对烘箱内部空气的流动状态影响很小，这一点与上述无模具模型的仿真结果是相似的。

从图5可以看出，对于3 m长的模具，在上叶片转角为40 °且下叶片转角为10 °的情形，模具表面温度的标准偏差最小，即此时模具表面的温度分布最均匀。这与图2和图4所示的最佳叶片转角组合情形都不一样。从图5还可看出，3 m长模具表面温度的标准偏差随叶片转角的变化幅度比图4所示2 m长模具的要小很多。按公式(1)算出的3 m长模具的叶片调整有效率仅为14.2 %，也远小于2 m长模具的叶片调整有效率。这是因为较长的模具在转动时对烘箱内部空气的搅动作用更加强烈，这使得通过调整叶片转角所造成的进气方向的改变对烘箱内空气流动状态的影响不再显著。因此当模具的长度与烘箱的内径之比大于0.85时，通过调整叶片的转角来改善模具表面温度分布的均匀性就意义不大。

对比图4和图5可以看出，如果不采用调整叶片，3 m长模具的表面温度分布比2 m长模具的更均匀。但采用调整叶片后，在所得的最佳转角组合情形下，3 m长模具的表面温度分布就不如2 m长模具的均匀。

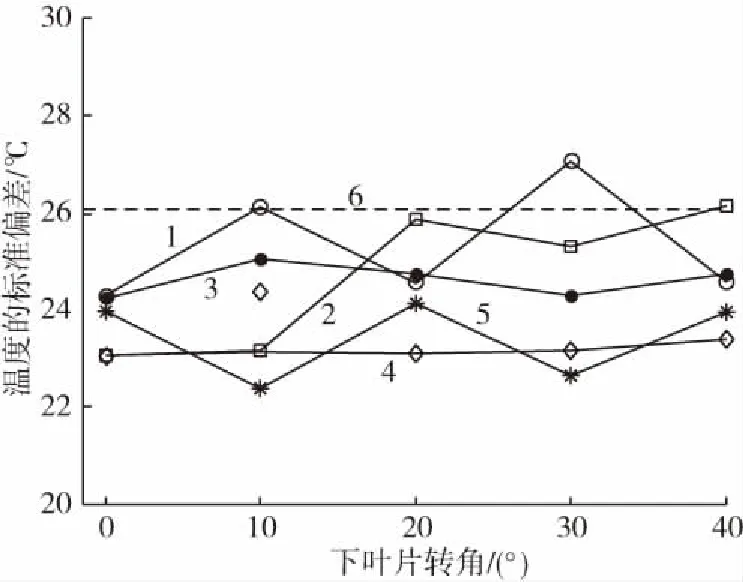
上叶片转角：1—0 ° 2—10 ° 3—20 ° 4—30 °5—40 ° 6—无叶片情形图5 3 m长模具表面温度的标准偏差随下叶片转角的变化Fig.5 Variation of standard deviation of temperature at 3 m long mould wall with the angle of lower vane

2.3 模具长度对模具表面温度均匀性的影响

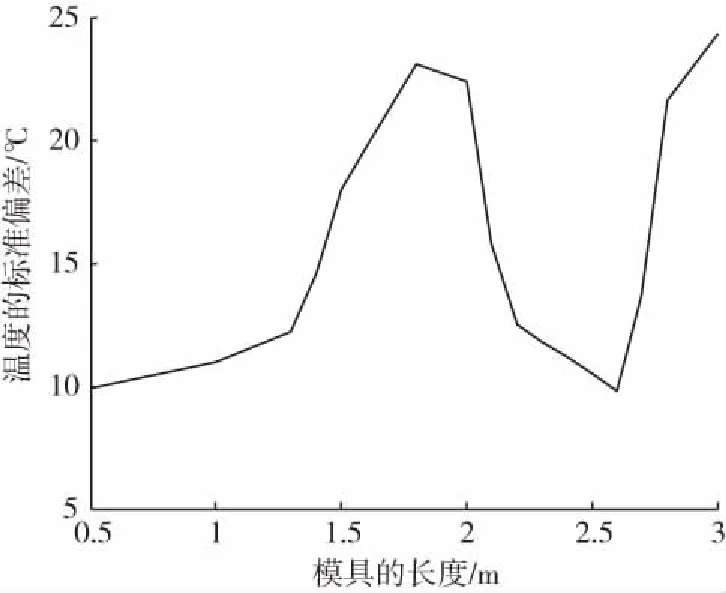
图6 当上、下叶片转角均为0 °时，模具表面温度的标准偏差随模具长度的变化Fig.6 Variation of standard deviation of temperature at mould wall with length of mould when both angles of upper and lower vanes are 0 °

图6显示了在上、下叶片转角均为0 °的情形模具表面温度的标准偏差随模具长度的变化规律。可以看出，模具表面温度的标准偏差是随着模具长度的减小而呈先快速减小然后增大最后再减小的趋势。当模具的长度小于1.3 m时，模具表面温度的标准偏差随其长度的减小而减小的速率变得越来越缓慢，即模具表面的温度分布慢慢趋于均匀。另外当模具的长度为2.6 m时，其表面温度分布也很均匀。

长度为3 m的模具虽然对烘箱内部空气的搅动程度很强烈，但由于模具端部与烘箱内壁面的间距较小，致使迎风区的热空气与背风区的冷空气很难彼此混合，因此模具表面温度分布的均匀性较差。随着模具的缩短，模具端部与烘箱内壁面的间距开始变大，内部空气在迎风区和背风区之间的流动和相互混合变得比较畅通，从而改善了模具表面温度分布的均匀性，使得模具表面温度的标准偏差开始减小。但另一方面随着模具变短，模具的转动对内部空气的扰动程度也会变得越来越弱，而这对改善模具表面温度分布的均匀性是不利的。当模具的长度减小到一定程度，模具扰动变弱对模具表面温度均匀性的不利影响要超过空气在迎风区和背风区之间流动混合畅通所带来的有利影响，从而使得模具表面温度的标准偏差又开始增大。当模具的长度继续减小到一定程度，模具转动对内部空气的扰动以及内部空气在迎风区和背风区之间的流动混合对模具表面温度分布的均匀性都不再有明显的影响。此时主要是由于模具的表面积越来越小，才使得模具表面温度的标准偏差又开始变小。

从图6可以看出，当上、下叶片转角均为0 °时，在模具长度为1.8 m和3 m处分别有2个温度标准偏差的高点，即在这2个模具长度，模具表面温度分布的均匀性最差。当模具长度为1.8 m时，叶片调整有效率比较高，所以还可以通过调整叶片的转角来有效地改善模具表面温度分布的均匀性。但是当模具长度为3 m时，如上所述叶片调整有效率比较低，即此时通过调整叶片的转角来改善模具表面温度均匀性的效果就不再明显。因此对于模具长度与烘箱内径之比大于0.85的情形，更多地需要通过其他的措施来改善模具表面温度分布的均匀性，如增大烘箱的进风速度[7]82或优化设计烘箱的结构。

3 结论

(1)在上、下叶片都设置为水平方向的情形，烘箱内部空气的温度分布最均匀；

(2)对于2 m长的模具，上叶片转角为0 °且下叶片转角为20 °时，模具表面的温度分布最均匀；对于3 m长的模具，上叶片转角为40 °且下叶片转角为10 °时，模具表面的温度分布最均匀；

(3)3 m长模具的叶片调整有效率远小于2 m长模具的叶片调整有效率；在模具长度与烘箱内径之比大于0.85的情形，通过调整叶片转角来改善模具表面温度分布的均匀性的效果不再显著；

(4)对于内径为3.5 m的圆筒形烘箱，在上、下叶片都设置为水平方向的情形，当模具的长度为1.8 m和3 m时，其表面温度分布的均匀性都很差。