次线性期望空间下广义ND序列的强大数定律

钟豪媛，吴群英

(桂林理工大学 理学院,广西 桂林 541006)

0 引言及引理

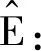
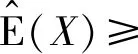
从定义中得出,对于所有的X,Y∈有

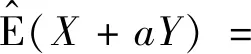
定义2令⊂,一个函数V:→[0,1]被称为容度,如果

1)V(∅)=0,V(Ω)=1;

2)V(A)≤V(B),∀A⊂B,A,B∈。

如果对于所有的A,B∈,有V(A∪B)≤V(A)+V(B),则称V具有次可加性,在次线性期望空间可产生上容度和下容度(,v),记Ac是A的补集,定义

根据定义, 则有

v(A)≤(A), ∀A∈。

如果I(A)∈,则有

(A)=

如果f≤I(A)≤g,g,f∈,则有

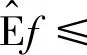
(1)

v(A∪B)≤v(A)+(B)和

定义3定义Choquet积分为

定义4*为

2) 如果I(A)≤g,g∈,那么*(A)≤进一步,如果是可数次可加的,那么

3)当I(A)≤g∈时,*是最大的满足*(A)≤的可数次可加的容度。

定义5(广义ND)在次线性期望空间下随机变量序列{Xn,n≥1}被称为上(相应的下)广义ND序列,如果存在常数K≥1,使得下式成立,

其中, 非负函数gi∈Cl,Lip(Rn),i=1,2,…,是非降(或非增)的。若序列既是上广义ND序列又是下广义ND序列,则称该序列是广义ND序列。

引理1[4]对于X∈, 如果那么|X|< ∞, a.s., 即(|X|=∞)=0。

引理2(Borel-Cantelli引理)假设{An,n≥1}是中的一列事件,V是可数次可加的容度,如果那么V(An, i.o.)=0, 其中

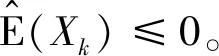
1 主要结果

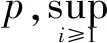
(2)

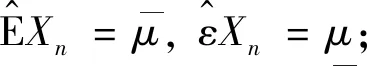
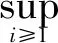
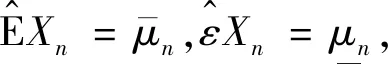
2 主要结果证明

证明过程中用到的c表示与n无关的正常数, 在不同的地方可表示不同的值。 定义an≪bn表示存在c>0, 使得对充分大的n都有an≤cbn。

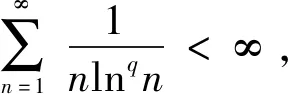
因为

所以要证明式(2)只需要证明

(4)

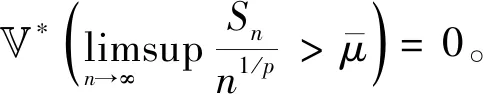
(5)

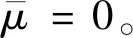
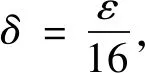
因为

先证明对于不同取值范围的p，有

(7)

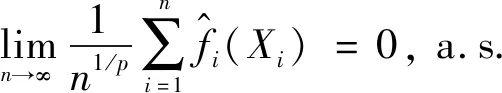
(8)

成立。

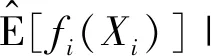
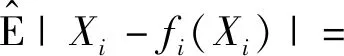
所以

(9)

令g(x)∈Cl,Lip(R)，使得对于所有的x,有0≤g(x)≤1,当|x|≤μ,g(x)=1; 当|x|>1,g(x)=0，则有

(10)

所以有

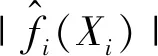
以及

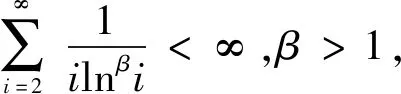
(11)

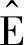
又根据引理1,有

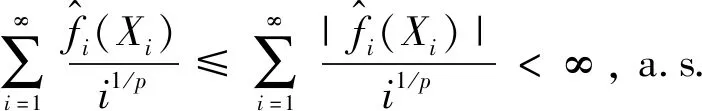
(12)

根据Kronecker引理和式(11)、(12),则式(7)和式(8)成立。

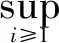
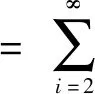
(13)

即可得到式(8)成立。 根据式(10)和Cr不等式得到

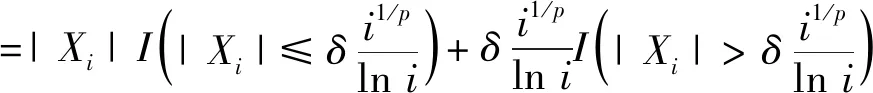
进一步,有

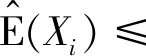
所以有

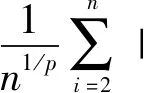
:=I+II。

(14)

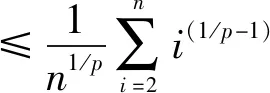
(15)

由Markov不等式得

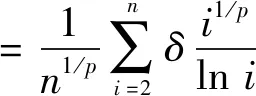
(16)

根据式(15)、(16)得到式(7)成立。

对式(6)左右两边取上极限,又根据式(7)和式(8),则有

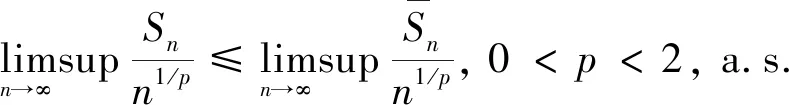
(17)

(18)

即可。

下面证明式(18)。

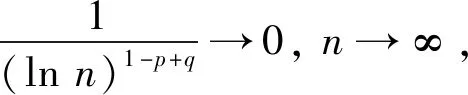
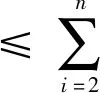
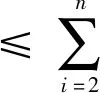
(19)

又因为

(20)

=exp(-2lnn)。

而

由于{Xn,n≥1}是广义ND序列,则{-Xn,n≥1}也是广义ND序列,因此{-Xn,n≥1}也满足定理1的假设条件,以-Xn代入式(4)得

整理得到式(4)。结合式(4)、(5),即证明了(2)成立。

则可推出

(21)

类似的,可令Zi=μi-Xi,则

继而可推出

(22)

根据式(21)、(22)，可得式(3)成立。