集成GA-PSO方法的转子系统多点不平衡量识别*

张茹鑫， 温广瑞,2， 张志芬， 徐 斌

(1.西安交通大学机械工程学院 西安，710049) (2.新疆大学机械工程学院 乌鲁木齐，830046)

引 言

振动问题是大型旋转机械面临的主要问题，而转子不平衡则是产生振动的重要原因[1]。经典影响系数动平衡方法要求转子多次试重启车来确定合理的平衡配重，平衡效率较低，操作代价高昂[2]。自20世纪70年代以来，国内外大量学者致力于开展不平衡量识别研究以实现无试重动平衡。文献[3-4]采用基于达朗贝尔原理的牛顿-欧拉公式建立转子系统运动方程，获得转子理论不平衡响应，与实测振动信号对比从而实现不平衡量大小和相位识别。文献[5]利用转子轴心轨迹作为评判标准，采用转子有限元模型获得系统响应，并将遗传算法与模拟退火相结合作为一种新的寻优算法，进行不平衡位置、质量和相位识别。Sudhakar等[6]通过建立转子有限元模型，采用等效载荷法识别转子实际不平衡量，极大地提高了动平衡效率。李晓丰等[7]通过对转子系统进行模态分析，结合影响系数法实现转子无试重动平衡。Sanches等[8]结合Guyan缩减方法和相关性分析，利用李雅普诺夫方程在时域识别不平衡参数。上述研究方法只进行不平衡量大小和相位识别，忽略位置信息；或者只在单点位置进行不平衡量识别，无法满足实际转子系统多轴系、多点、多面和多角度考虑的综合需求[9]。

智能优化算法相对传统优化算法，为解决多项式复杂程度的非确定(non-deterministic polynomial, 简称NP)问题提供了一条全新的途径，近年来成为国内外学者关注的研究热点[10]，在系统控制、人工智能、模式识别和生产调度等领域得到了迅速推广和应用[11]。笔者尝试利用智能优化算法，与传统转子动力学结合，正反问题角度相结合实现转子多点不平衡量的准确识别，对于后续缩短现场动平衡时间，提高动平衡效率，减少平衡过程启停机等方面具有重要的意义。

基于遗传算法良好的全局寻优能力和粒子群算法局部寻优的特性，笔者结合二者优势，将其集成应用于转子多点不平衡量识别，实现转子多点不平衡量数目、位置、质量和相位信息的全面识别，并通过实验验证了该方法的有效性和实用性，为现场精准动平衡提供指导。

1 基本思想

基于模型的处理方法是将测量振动信号与模型相结合，对系统状态进行评估的方法，定量获得系统的状态信息[12]。笔者采用此方法对转子系统进行不平衡量识别，通过建立转子系统模型，获得转子系统理论不平衡响应，并与实测振动信号进行对比，利用智能优化算法获得转子不平衡量信息。由于需对整个转子系统多节点不平衡量同时进行识别，每个不平衡量信息又包括不平衡数目、位置、质量和相位，整个转子系统待识别目标较多，直接使用智能优化算法难以实现。因此，将多点不平衡量识别过程分为两步，先进行不平衡量数目识别，再进行位置等其他信息识别，识别流程如图1所示。

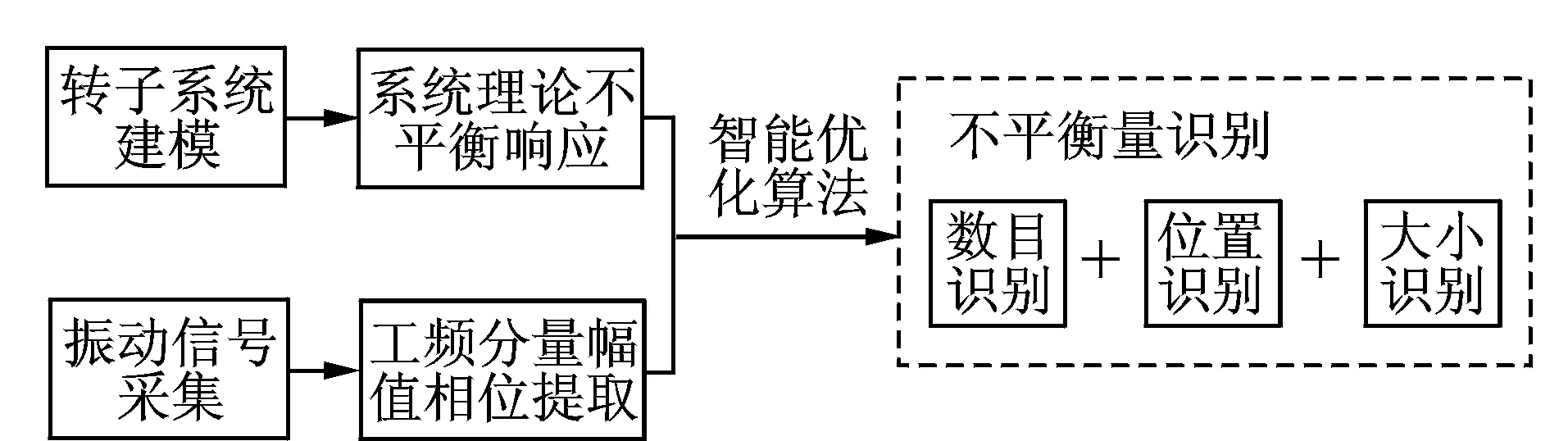
图1 转子不平衡量识别流程图Fig.1 Flow chart of rotor unbalance identification

2 算法原理及方法

转子多点不平衡量识别过程主要包括实测信号工频分量提取、系统理论响应求解和不平衡量识别3部分，识别部分又包括数目识别和其他信息识别两方面。转子不平衡信号工频分量幅值和相位的提取，可通过比值校正快速傅里叶变换(fast Fourier translation，简称FFT)进行[13]，本方法关键之处在于转子建模、理论响应求解以及后续基于优化算法的准确识别。

2.1 转子建模及理论响应求解

工程实际中广泛采用转子离散质量模型对转子进行建模，并求取转子不平衡响应。常用的方法包括传递矩阵法和有限元法[14-15]等。其中，Riccati传递矩阵法保留了传递矩阵法的所有优点，数值稳定、精确度高，理论计算结果与现场实测值较接近，且占用内存小、计算速度快。

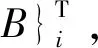
设构件所受外力为Ff和Fe，则构件两端截面矢量关系为

(1)

其中：Ti为第i个构件的传递矩阵。

通过转子系统划分各构件长度l、质量m、弹性模量E，泊松比ν、截面影响系数a和轴承刚度、阻尼等信息，利用文献[15]中的方法可计算出Ti，Ff和Fe。上述参数皆为转子系统固有参数，可通过相应测量获取。

引入Riccati变换

fi=Siei+Pi

(2)

式(2)建立了同一截面状态参数间的关系，同式(1)联立求解，可得到Si，Pi和ei的递推公式。根据左端界面的边界条件fi=0，ei≠0和右侧边界条件fn+1=0，即可递推出各截面状态矢量ei，即转子不平衡响应。

2.2 基于GA的不平衡数目识别

基于获取的转子理论响应，采用智能优化算法对比分析实测振动信号，寻求一组不平衡量，使理论响应与实测信号尽可能一致。由于该过程需优化参数较多，故将不平衡识别分为两部分，首先进行不平衡量数目识别。

目标函数合理选取与否将直接影响寻优结果，进行不平衡数目识别时，需直接对转子系统所有节点进行优化，若只采用传统的残余振动平方和作为目标函数，不能得到较好的识别结果。基于上述原因，笔者尝试引入正则化思想构造新的目标函数。

2.2.1 正则化目标函数构造

不平衡量识别是一个逆问题的求解过程，由于逆问题的病态特性，对逆问题的直接求解一般被认为是不适定的[16]，正则化方法是处理逆问题中经常使用的一种方法[17]。正则化核心是对最小化经验误差函数添加约束，使得优化过程倾向于选择满足约束的方向，最终得到满足一定条件的最优解。L1范数正则化通过向目标函数中添加L1范数，使寻优结果满足稀疏化的条件。

本研究涉及的转子系统若划分N个节点，则不平衡量存在的节点数目远小于N，即大部分节点处不平衡量很小或为零。若用一个1×N的向量U表示转子不平衡量分布情况，则向量U为一个稀疏向量。考虑在传统目标函数即残余振动平方和最小的基础上增加L1正则项，形成新的目标函数，得到不平衡量稀疏性的结果

(3)

其中：U为转子不平衡量向量；xr为转子系统实测振动信号；f(U)为系统理论不平衡响应；λ为正则化因子。

因不平衡量分布情况复杂，故此处所选正则化因子非传统常数正则化因子，通过不平衡振动和节点位置有关的函数式(4)来确定

λ=C/K(xr)/h(n)

(4)

其中：C为常数；xr为转子系统实测振动信号；K(xr)为关于xr的二次函数；N为节点位置；h(n)为关于节点位置n的函数。

h(n)函数可看作惩罚因子，对于同一不平衡量，若其位置距离轴承越近，h(n)值越大，目标函数值则越小，从而避免识别结果集中在转子距离轴承最远的节点位置，是一种无量纲参数。以节点数N=14为例，h(n)函数如图2所示。

图2 h(n)函数示意图Fig.2 Function image of h(n)

2.2.2 基于遗传算法的不平衡量数目识别

转子不平衡量识别是一个复杂的非线性规划问题，目前常用的智能优化算法包括遗传算法和蚁群算法等，并已成功应用于多类学科的优化领域[2,18-19]。遗传算法使用随机搜索技术，具有很好的全局搜索能力，能够以较大的概率实现最优解的搜寻，且同时使用多个搜索点的搜索信息，并行处理能力强，鲁棒性好。笔者选择遗传算法作为不平衡量数目识别部分的优化算法。

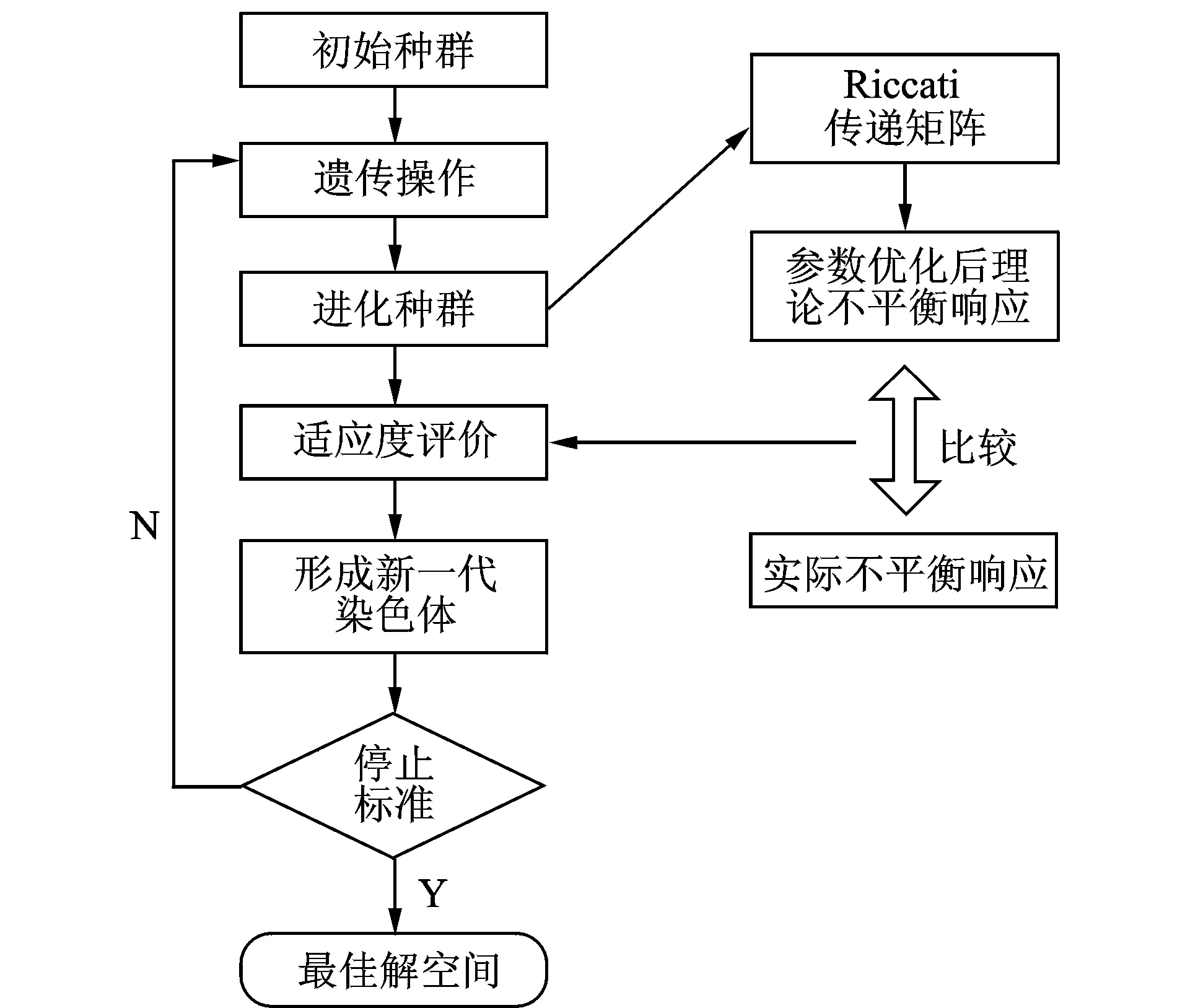
图3 GA识别不平衡量数目流程图Fig.3 Flow chart of unbalanced number identification by GA

采用二进制编码方式，采用式(3)所示的正则化目标函数作为适应度函数进行不平衡量数目识别，识别流程如图3所示。识别过程中忽略振动相位信息，只保留振动幅值信息，在保证识别结果正确率的同时简化计算过程，提高计算效率。

2.3 不平衡其他信息识别

采用GA完成不平衡量数目识别后，将最优向量的非零元素数目保留，作为转子系统不平衡数目。在此基础上进行不平衡位置和大小识别。粒子群算法是一种常用的智能优化算法[20-21]，采用群体解的合作机制来迭代产生最优解，需调节参数较少，具有良好的局部寻优能力，收敛速度快。相比GA算法识别时间更短，局部寻优精度更高。笔者选用PSO进行不平衡位置大小识别，流程如图4所示。

图4 PSO算法识别不平衡量位置大小流程图Fig.4 Flow chart of rotor unbalanced location and mass identification by PSO

不平衡位置和大小识别通过两步完成。首先进行不平衡量位置识别，忽略相位信息，通过识别0°方向等效不平衡量位置，确定实际不平衡量位置，位置确定后则进行下一步质量和相位识别。由于PSO算法对种群初始状态比较敏感[22]，故初值的选取对优化结果较为重要。不平衡量识别过程中，由于不平衡量越大，振动信息越丰富、越易识别，因此使用PSO进行优化时，初值选取并非直接优化变量的整个范围，而是根据不平衡量识别的特点，适当缩小初值选取范围，进而采用节点理论响应与实测信号之差平方和作为目标函数进行识别。仿真数据和实验数据表明，参数调整后能很好地提高识别准确率。

3 仿真数据分析

3.1 转子实验台模型

用于分析研究的转子-轴承系统模型如图5所示，划分为13个轴段，14个节点，转子的两端由滑动轴承支承，轴上分布2个转盘。转子系统结构信息如表1所示。结构参数通过直接测量转子系统获得，轴承参数通过查阅相关文献获得。

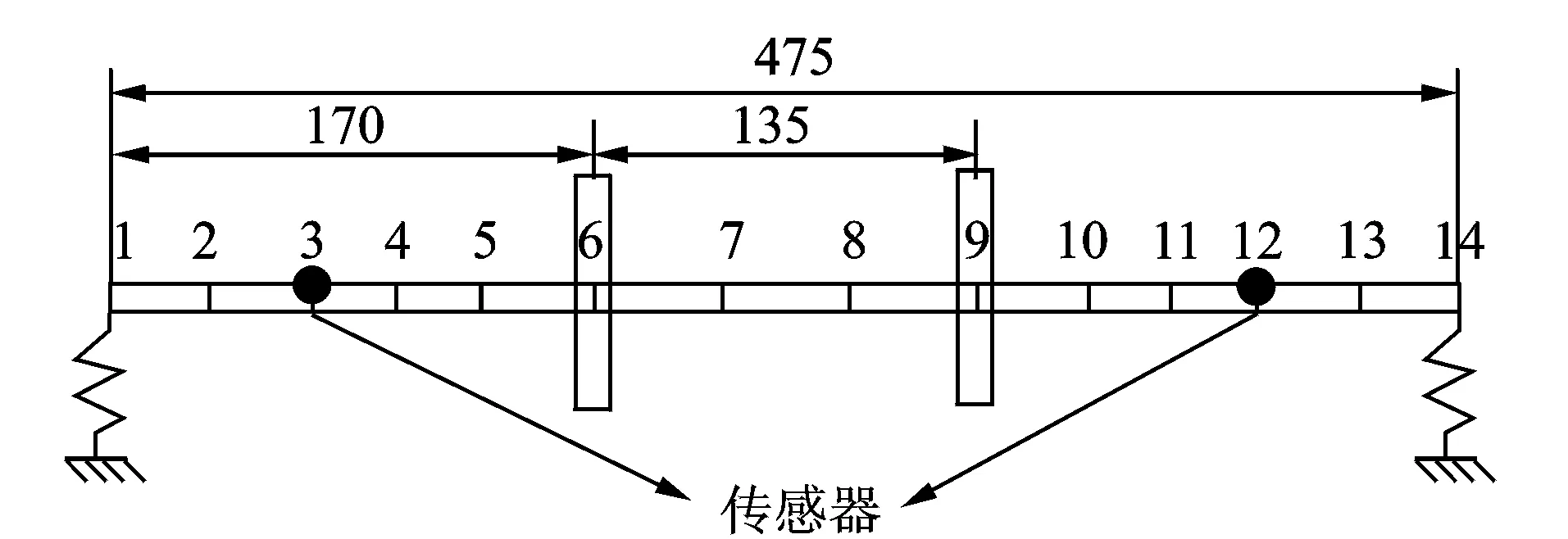
图5 转子系统模型(单位：mm)Fig.5 Rotor system model (unit: mm)

3.2 不平衡量识别

采用Riccati传递矩阵计算转子不平衡响应后,利用遗传算法进行不平衡量数目识别。采用二进制编码，个体长度为2，种群大小为50，收敛标准为最大进化代数。由于本研究方法主要依靠遗传算法的全局搜索能力，故选择单点交叉和多点交叉相结合的交叉操作及较大的变异幅度，分别设为0.7和0.08。设置不同数目、大小和相位的不平衡量，数目识别结果如表2所示(表中“，”前后节点位置、不平衡质量和不平衡相位一一对应)。可以看出，添加正则化项的遗传算法可以准确识别转子3种情况下不平衡量数目。

不平衡数目确定后，采用粒子群算法进行不平衡量位置和大小识别。种群个数选择100，不平衡质量优化范围为0～100 g·mm，初值采用直接优化变量的整个范围和缩小优化范围至0～45 g·mm的识别结果对比如表3所示。可以看出，通过适当缩小粒子群算法初始化范围，极大地提高了位置识别准确度。初值改进后的粒子群算法对单点不平衡量和双点不平衡量位置都可准确识别，对于三点不平衡量，可对其分布具有良好的估计。后续位置和大小识别将对初值改进前后的粒子群算法进一步对比。

表1 转子系统结构信息Tab.1 Rotor system information

表2 模拟数据不平衡数目识别结果

Tab.2 Unbalanced number identification of simulation data

节点位置不平衡质量/(g·mm)不平衡相位/(°)识别数目620 01650 451680 9015,735,350,9025,750,500,9025,780,80 0,9026,7,935,35,350,45,9036,7,950,50,500,45,9036,7,980,80,800,45,903

不平衡位置确定后进行不平衡质量和相位信息识别。因三点不平衡位置识别并非完全准确，故只进行单点不平衡量和两点不平衡量识别。初值改进前后单点不平衡量识结果如图8，9所示。识别误差如表5所示。上述图别结果如图6和7所示。识别误差如表4所示。初值改进前后两点不平衡量识别表证明，对于单点不平衡量，初值改进前后两种粒子群算法识别结果相差不大，都较为准确，故后续对于单点不平衡量不再进行初值改进效果对比，仅采用初值改进后粒子群算法进行识别。对于两点不平衡量，初值改进后质量和相位识别结果正确率都有较大提高，获得较为理想的识别结果。

图6 初值改进前模拟数据单点不平衡量识别结果(单位：g·mm)Fig.6 1 unbalance identification of simulated data based on original initial value (unit: g·mm)

表3 模拟数据不平衡位置识别结果Tab.3 Unbalanced location identification of simulation data

表4 模拟数据单点不平衡量识别结果及误差

Tab.4 The error of single unbalance identification of simulated data

序号节点位置不平衡质量/(g·mm)不平衡相位/(°)初值改进前识别质量/(g·mm)初值改进前识别相位/(°)初值改进后识别质量/(g·mm)初值改进后识别相位/(°)1620020360.9620359.802650455045.265045.003680908091.678089.95平均识别误差/%00.5400.05

表5 模拟数据两点不平衡量识别结果及误差

Tab.5 The error of 2 unbalances identification of simulated data

序号节点位置不平衡质量/(g·mm)不平衡相位/(°)初值改进前识别质量/(g·mm)初值改进前识别相位/(°)初值改进后识别质量/(g·mm)初值改进后识别相位/(°)1535021.8741.8332.7110.377359027.6857.3030.0285.372550078.2437.2450.074.0397509015.05131.7846.9989.953580068.3313.1874.8410.947809067.7380.2169.4185.94平均识别误差/%35.7916.347.773.16

图7 初值改进后模拟数据单点不平衡量识别结果(单位：g·mm)Fig.7 1 unbalance identification of simulated data based on improved initial value(unit: g·mm)

4 实验验证

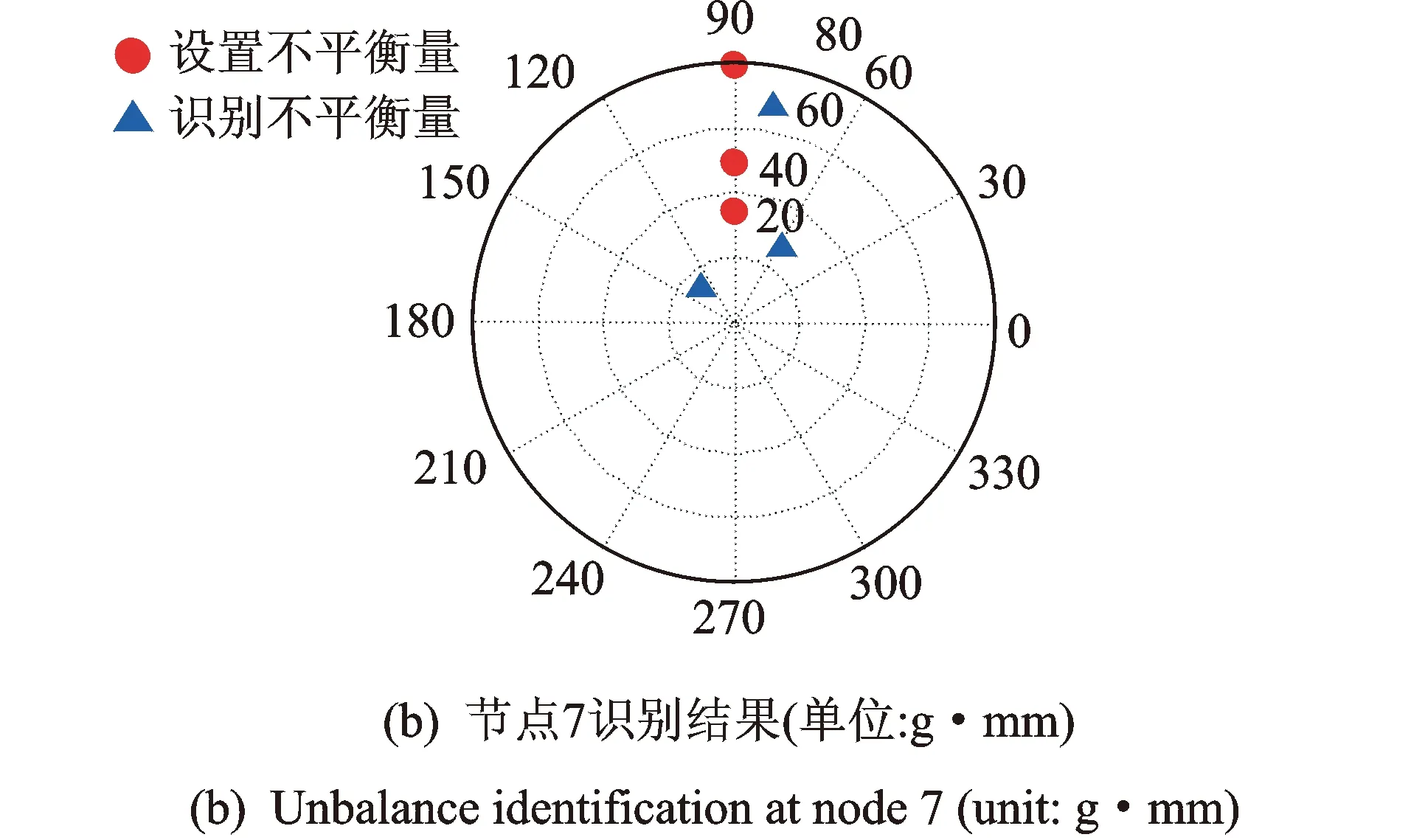
图8 初值改进前模拟数据两点不平衡量识别结果Fig.8 2 unbalances identification of simulated data based on original initial value

图9 初值改进后模拟数据两点不平衡量识别结果Fig.9 2 unbalances identification of simulated data based on improved initial value

图10 转子实验台Fig.10 The rotor test rig

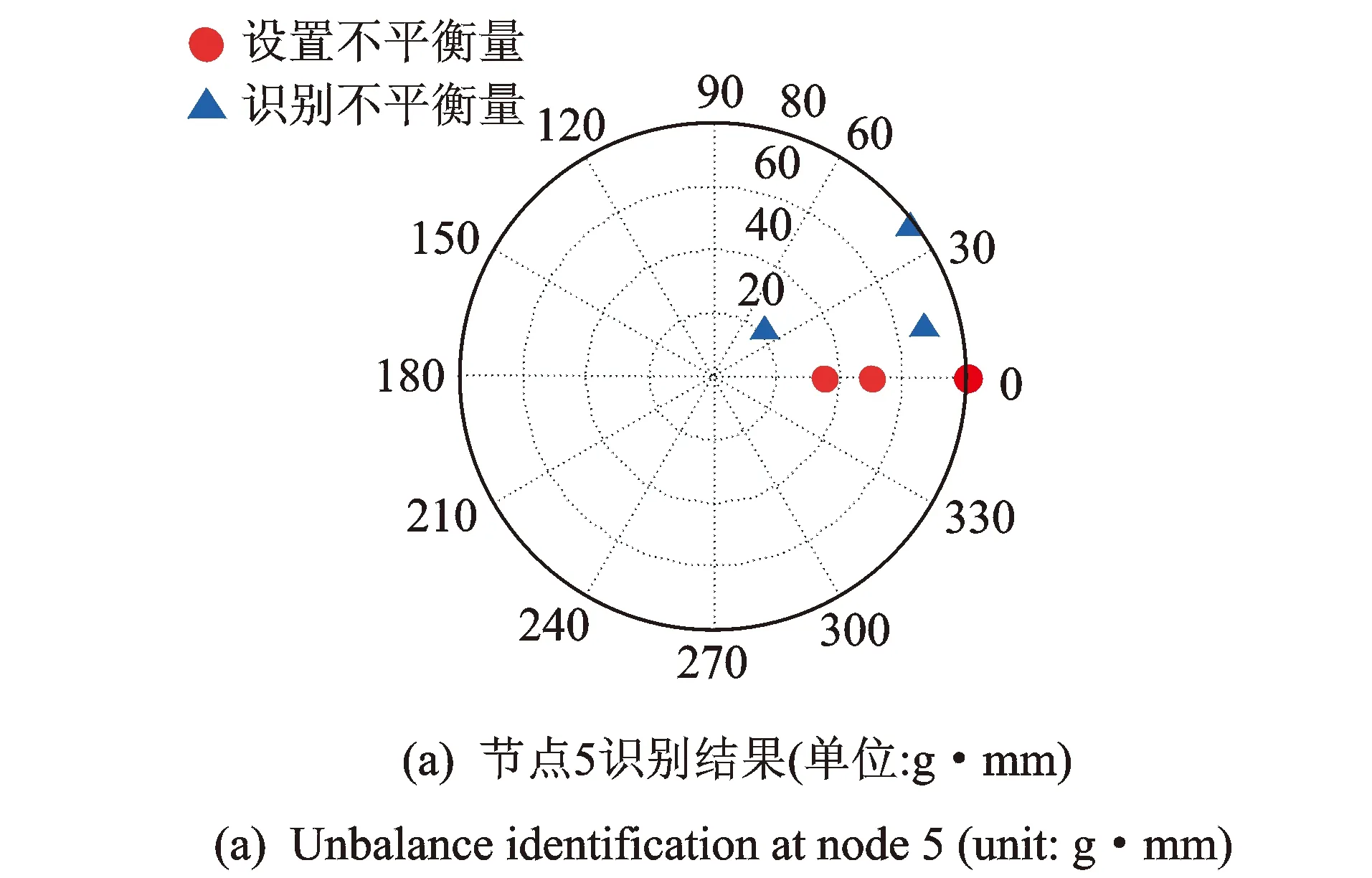
图11 实验数据单点不平衡量识别结果(单位:g)Fig.11 1 unbalance identification of experimental data (unit:g)

转子实验台如图10所示，传感器支架固定2个相互垂直的电涡流传感器，用以测量轴承附近转子径向振动，结构参数和转子模型一致。经过模型数值计算，该转子系统的第1, 2阶临界转速分别为1 608 r/min(实测为1 640 r/min)和7 098 r/min。

系统模型表明转子实验台两个转盘分别位于节点6和节点9，故在上述节点处设计不平衡量，通过在转盘不同方位添加配重块实现多种不平衡量设置。将多次实验结果表示在一张图中，单点不平衡量数目和位置识别结果如表6所示。质量和相位识别结果如图11所示。识别误差如表7所示。两点不平衡量数目和位置识别结果如表8所示。初值改进前后质量和相位识别结果如图12，13所示。识别误差如表9所示。

图12 初值改进前实验数据两点不平衡量识别结果Fig.12 2 unbalances identification of experimental data based on original initial value

表6～9结果表明，基于GA-PSO的不平衡量识别方法对于单点不平衡量识别效果良好，数目和位置识别完全正确，平均质量识别误差为11%左右，相位识别误差不超过1%。对于两点不平衡量，初值改进前后识别结果有较大差别，改进后转子不平衡量位置识别正确率大幅提高，位置识别完全准确，平均质量识别误差为12%左右，相位误差为3%左右，质量识别正确率提高了53.50%，相位识别正确率提高40.79%。

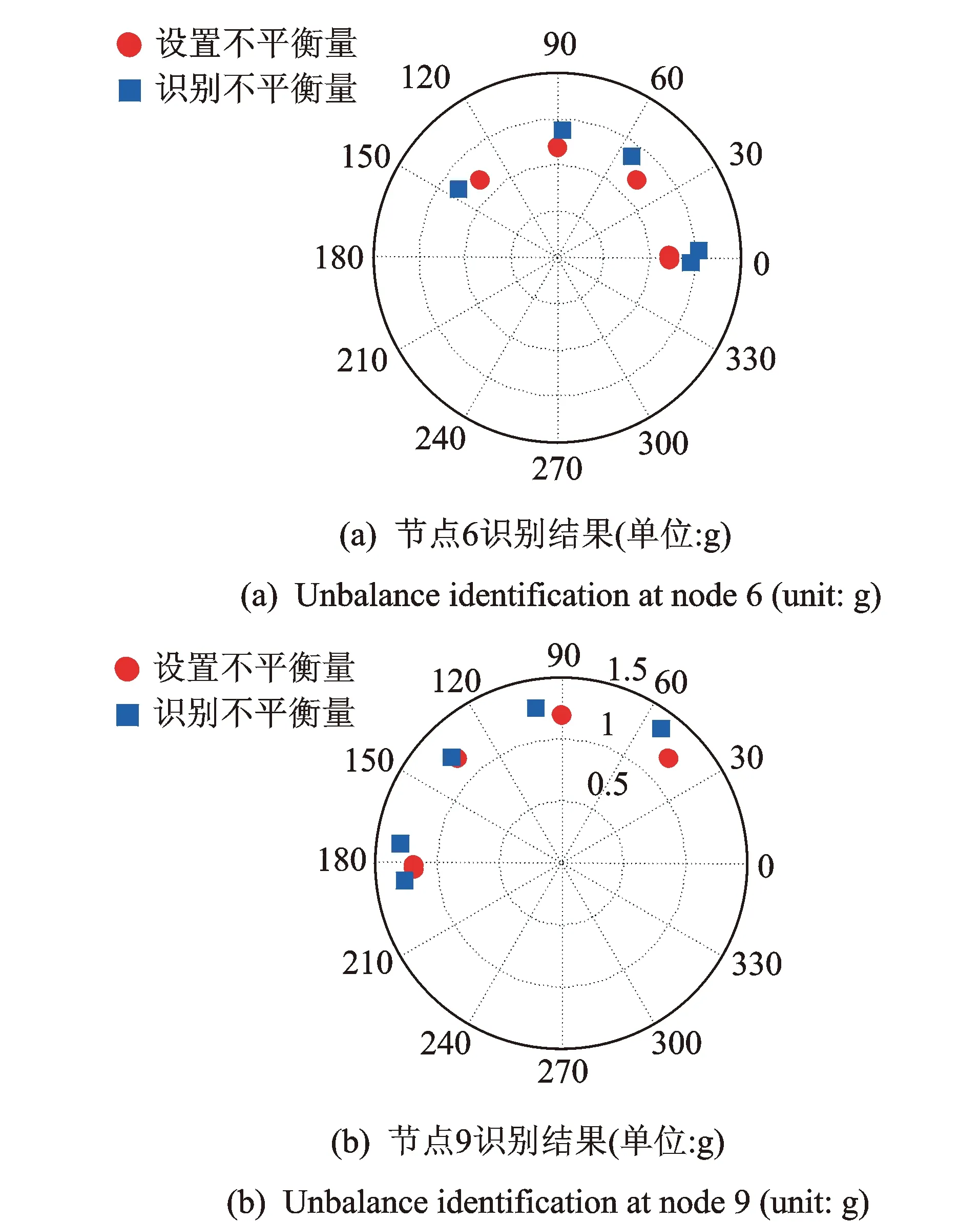
图13 初值改进后实验数据两点不平衡量识别结果Fig.13 2 unbalances identification of experimental data based on improved initial value

表6 实验数据单点不平衡量数目和位置识别结果

Tab.6 Unbalanced number and location identification of 1 unbalance of experimental data

序号节点位置不平衡质量/g不平衡相位/(°)识别数目识别位置160.8016261.631516361.2016461.24516561.29016661.213516761.218016861.222516961.2270161061.231516

表7 实验数据单点不平衡量结果及误差Tab.7 The error of single unbalance identification of experimental data

表8 实验数据两点不平衡量数目位置识别结果Tab.8 Unbalanced number and location identification of 2 unbalances of experimental data

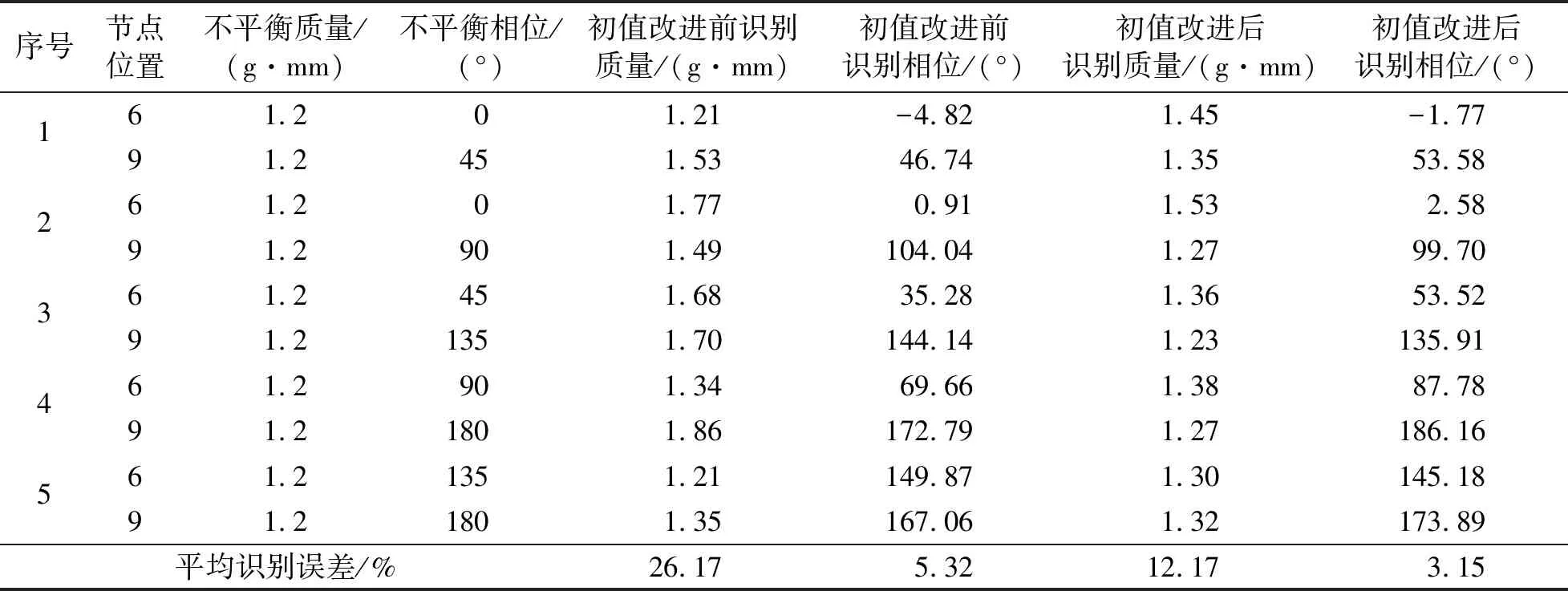
表9 实验数据两点不平衡量结果及误差Tab.9 The error of 2 unbalances identification of experimental data

从图11，13结果可发现，与理论值相比，识别结果整体偏大。分析原因，可能是由于转子模型简化引起的误差，从而造成识别有所偏差。综上，基于遗传算法和粒子群的不平衡量识别方法对转子多点不平衡量具有较好的识别效果，即使在某些复杂工况下识别结果出现偏差，但仍可对不平衡量进行良好的估计，且在现场动平衡中，相比质量信息，相位信息更加重要，因此该方法可对现场无试重动平衡提供精确的指导。

5 结 论

1) 对于转子系统单点和两点不平衡量，基于GA-PSO的方法能够准确识别其数目、位置、质量和相位信息。

2) 对于转子系统多点不平衡量，基于GA-PSO的方法能够准确识别其数目，并对其位置进行良好的预估，为后续动平衡或转子维护做准备。

3) 实验结果表明，基于GA-PSO的方法识别出的转子系统不平衡量与实际存在的不平衡量相吻合，验证了该方法的有效性，后续可进一步应用于转子系统在线不平衡的预估与无试重现场动平衡。