调频步进信号目标抽取快速算法研究

杨 磊 郭鹏程 罗丁利

(西安电子工程研究所 西安 710100)

0 引言

调频步进信号是一种重要的距离高分辨率雷达信号，它通过发射一串载频线性跳变的脉冲，再对回波进行IFFT处理来获得合成距离高分辨的效果。调频步进信号是合成宽带信号，它将宽带信号在频域分解成多个窄带信号，通过多个窄带信号的收发来获取合成的宽带信息，可以在获得高分率的同时降低对数字信号处理机的瞬时带宽的要求，系统易于工程实现。

在调频步进雷达体制中，目标冗余是一个特殊的问题。因此需要采用目标抽取算法来消除目标冗余。目标冗余是指IFFT细化后的距离范围与当前回波采样值所表示的距离范围不是简单的一一对应关系，有一些多余的信息。要得到真实的距离信息,就必须精确地按照一定的顺序,从所有采样点的IFFT结果中选取某些点，去掉冗余信息，组成完备的一维距离像，这就是调频步进雷达的目标抽取算法。

1 目标抽取算法

冗余分为两种：距离失配冗余和过采样冗余[1]，其中距离失配冗余与单个脉冲距离分辨率rT，单点不模糊距离rI有关；而过采样冗余主要由单个脉冲距离分辨率rT，单个脉冲距离精度rs决定。

1.1 距离失配冗余

单个脉冲的距离分辨率由其信号带宽B决定，即rτ=C/(2·B)，其中C为光速。步进频的信号的分辨率由其合成带宽决定，即rb=C/(2·N·Δf)，N为合成信号的脉冲个数[2]。则一个采样点的距离范围为rI=rb·N=C/(2·Δf)。rτ与rl的比值为rτ/rI=Δf/B。通常，步进频率信号需要满足条件：Δf/B<1，它表示一个采样单元中的有效距离小于可表示的距离范围，所以会有rI-rτ的区域无效(即冗余)，此时的高分辨结果包含了全部目标的信息，但是由于距离失配，会造成目标的距离测不准，必须通过去冗余算法获得真实的距离。

图1是上述情况下3组相邻采样点IFFT后的结果示意图。由图1可以看出，每组采样点的IFFT结果有rI-rτ的无效区域，需要采用一定的目标抽取算法，提取出每个采样点中目标所占的有效区域，即将图1中的1、2、3、4提取出来续接获得真实的一维距离像。

图1 相邻采样点IFFT后示意图

1.2 过采样冗余

理论上，采样周期Ts只要等于信号发射脉宽τ，就可以获得完整的一维距离像，但是由于实际中回波的展宽，会使得有一定概率采不到回波的最大值，造成幅度损失。所以通常会使Ts≤τ/3 ，从而降低采样损失[2]。但提高采样率会使同一个目标的回波出现在多个相邻的采样点，在合成距离像拼接时产生虚假目标的现象，所以需要有效的目标抽取算法来去除虚假目标。

目前，常用的目标抽取算法主要有如下两种：

1)舍弃法

图2 舍弃法原理图

舍弃法原理如图2所示，设共有M个采样点，IFFT后可以得到N个数据，从而得到一个大小为N×M的矩阵。对于其中第m个采样点，取出其中第Pm到第Qm点之间的Wm个数据(图2中的阴影部分)，作为当前采样点的提取点迹，再将每个采样点所取的数据进行拼接，即得到目标的一维距离像。关于Pm和Qm的取值由下式决定：

①对于第0个采样点，设P0=0，则W0=Trunc(rs/Δr)，Q0=P0+W0-1。

②对于第m个采样点，有Pm=(Qm-1+1)ModN

(1)

Qm=(Pm+Wm-1)Mod(N)

式(1)中，Trunc表示截断运算；Mod表示取余运算；Δr=C/(2NΔf)为雷达的最小分辨距离单元。

运算简单是舍弃法的最大优点。舍弃法是将当前IFFT结果有效区域的起始部分作为距离信息保留下来，但是对于采样周期小于信号脉宽的情况，此时目标刚刚进入当前采样点，并未获得幅度的最大值，所以该方法提取出的目标的信噪比较低，不利于后续的检测，这是舍弃法最主要的缺点。

2)同距离选大法

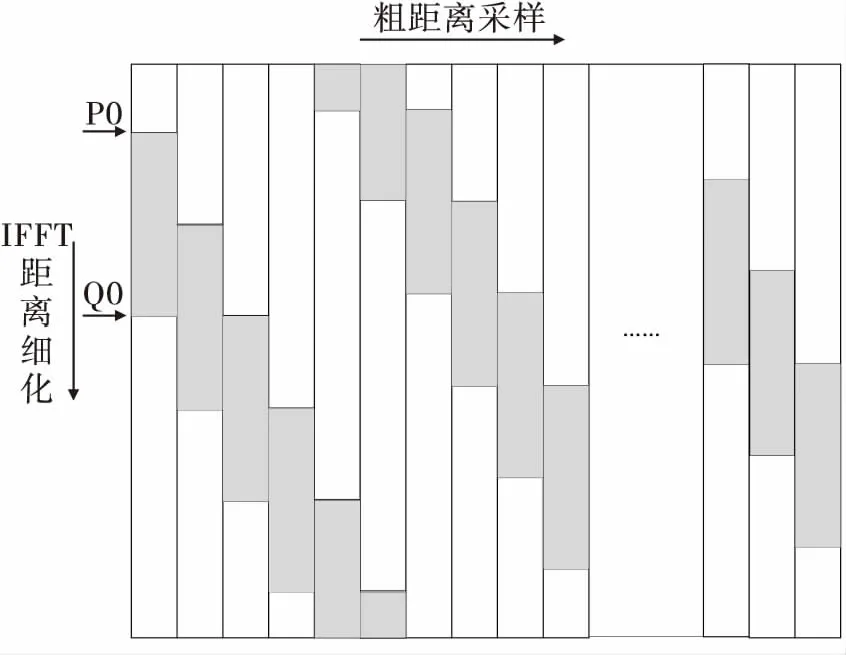
图3 选大法原理

同距离选大法从每个采样点中取出与脉宽τ相对应的距离范围，由于采样率大于信号的脉宽τ，所以相邻采样点会有部分重叠区域。同距离选大法将相邻的采样点提取的结果进行同距离比较，取出幅度较大的点作为提取结果。依照式(1)确定第m个采样点IFFT结果的提取起始点Pm，但是提取的数据个数不为Wm，而是由式(2)确定

(2)

如图3所示，阴影部分为每个采样点选取的数据，可见相邻的两个采样点之间有重合部分，重合的点数为Xm-Wm。对于重合部分的数据，取出幅度较大的作为输出。同距离选大法在静目标条件下，可以很好地得到目标抽取结果，能获得目标幅度的最大值。但是计算量较大，且在有距离走动时会出现伪峰[4]。

2 改进的抽取算法

传统的目标抽取算法首先需要对起始采样点(即第0个采样点)的位置做出标定，然后从起始位置顺次拼接各个采样点中的有效信息[5]，这种处理方法在工程中需要消耗较多的时间资源，而实际上我们仅仅关心波门内目标的回波信息，并不需要做全程拼像，基于以上问题，本文提出一种局部快速目标抽取算法，如图4所示，在一帧数据中，先确定目标的大概位置，再在目标所在大概位置的前后划定一个搜索区域，在该区域内选取最大值作为目标所在的细距离点。根据目标所在的位置以及距离细化程度确定该粗距离采样点上抽取范围的起始点以及终点，再向前和向后进行抽取，将抽取后的距离范围进行拼接，从而得到一维距离像。

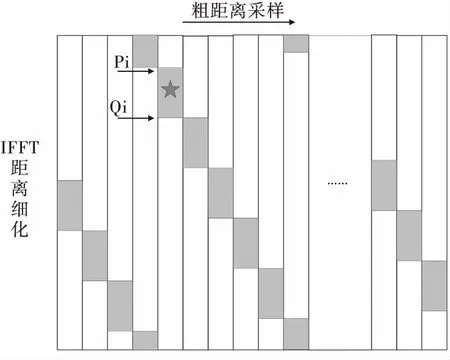
图4 改进算法的原理图

关于目标支撑区的起始点和终止点的选取，可以根据不同的任务需求来进行设置。首先，在对目标距离像进行抽取之前，一般需要对IFFT后的二维平面做恒虚警处理，去除干扰的噪声和杂波分量，仅保留目标的散射点回波。针对地面感兴趣的车辆目标，其回波距离像的支撑区长度一般不超过10m，且相邻散射点的间隔不超过5m，所以，根据一些先验知识，可以将拼像的长度设置为77个多普勒单元，距离维聚类的门限设置为15个多普勒单元。

抽取算法的流程如图5所示，具体步骤为：

图5 抽取算法的流程图

1)在波门内搜索回波幅度最大的散射点所在的位置，确定最大值所在的采样点R和多普勒C，记该点为A(R,C)，以A为中心，向两侧搜素，当出现新的幅度大于0的点Q时，判断该点的多普勒和A点的多普勒差D，若差小于设定的聚类门限T，则认为该点与A同属同一个目标，然后以该点为起点在向前搜索，直到当连续T个点都没有回波出现或长度超出了拼像的距离窗长度L时，停止向前搜索；

2)后向的搜索处理流程与前向相同；

3)拼像结束后，将找到的点及其对应的过采样点从原始的IFFT二维平面中删除，然后开始拼下一个目标的距离像。

该方法避免了寻找拼像起点的步骤，且不需要对全距离段的距离像进行处理，同时，算法采用聚类的方式确定目标距离像的起始和终止位置，可以保证拼到目标完整的距离像，又可以将两个距离像进行区分。

3 仿真与分析

如图6(a)为某调频步进体制雷达单帧回波的IFFT二维平面，波门宽度为60个采样点，数据经过恒虚警检测处理后，仅剩余两个目标的回波，图6(b)为目标回波区域的局部放大。两个目标的径向距离相差6m，即20个多普勒单元，拼像的距离窗长选择77个多普勒单元，聚类的门限设置为15个多普勒单元。

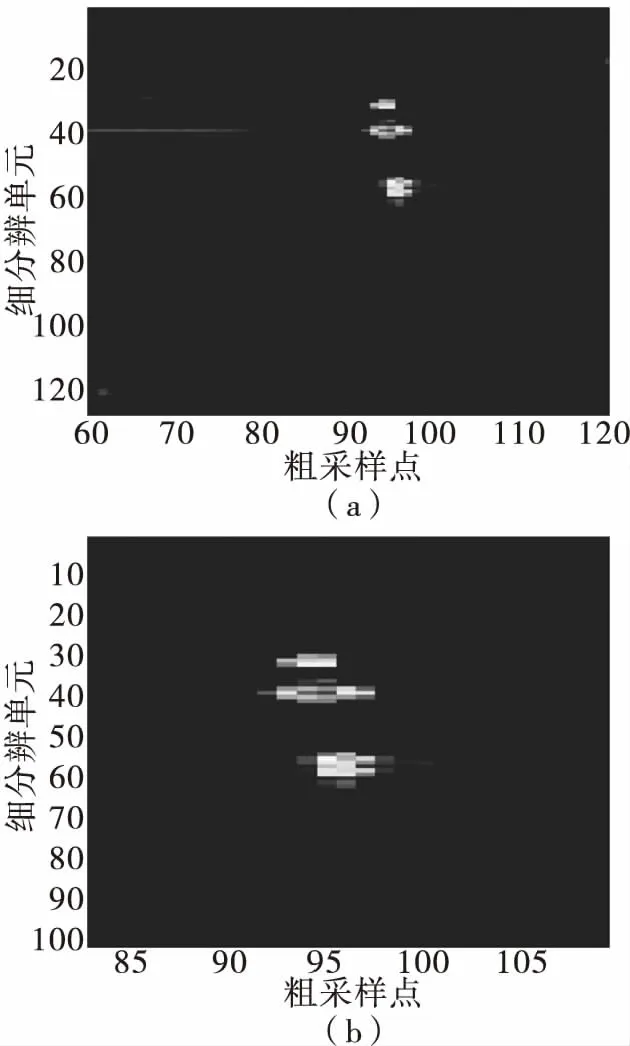
图6 雷达单帧回波的IFFT二维平面

如图7所示，如果不采用聚类的拼像算法，会将两个目标拼到同一幅距离像中，用本文所提算法，则可以将两个目标的距离像分别提取出来，拼像的结果分别如图8(a)和图8(b)所示。

图7 不采用聚类的拼像结果

图8 采用聚类的拼像结果

同时，由于采用了去除过采样点的处理，避免了再次搜索最大值时，目标一的过采样点对目标二的影响。

4 结束语

传统的目标抽取算法首先需要对起始采样点的位置做出标定，然后从起始位置顺次拼接各个采样点中的有效信息，这种处理方法在工程中需要消耗较多的时间资源，利用本文所提出的目标抽取算法则不需要寻找起始采样点，同时，由于聚类的算法可以自动地确定目标支撑区的起点和终点，并将径向上存在一定距离的两个目标区分开来。仿真实验验证了算法的有效性。