二元非结构肥效模型构建及其田间试验验证*

章明清 李 娟 章赞德 许文江 姚建族

（1 福建省农业科学院土壤肥料研究所，福州 350013）（2 大田县农田建设与土壤肥料技术推广站，福建大田 366100）（3 福建省亚热带植物研究所，福建厦门 361000）（4 福建省永春县农业技术推广站，福建永春 362600）

多项式肥效模型是实现农作物计量施肥的主要技术手段［1-4］。但在施肥实践中，这种基于多项式函数形式构建的经验肥效模型，因建模成功率偏低，严重制约了推荐施肥的精确性和模型的实用价值。就常用的二次多项式肥效模型而言，典型一元肥效模型比例仅占60%左右，典型二元肥效模型则仅有40.2%［5-6］，而典型三元肥效模型比例更低至23.6%［7］。即使采用蒙特卡洛建模法［8］，二元和三元二次多项式典型肥效模型的比例也仅有56.7%和37.3%。针对多项式肥效模型在应用中存在的问题，国内外学者在肥效模型选择及其适用性［9-11］、试验设计与参数估计方法［8,12-13］、类特征肥效模型构建［14-16］及非典型式推荐施肥优化方法［8］等方面进行了深入研究，提出了诸多改进措施，但对模型设定本身是否合理及其改进方法至今仍然鲜见研究报道，相关问题长期未能得到较好解决。研究表明，模型设定偏误［2］及由此引起的多重共线性和异方差［17-19］等问题是导致二次多项式肥效模型建模成功率偏低的重要原因。为此，作者构建了水稻一元非结构肥效模型［20］，克服了二次多项式肥效模型存在的上述缺陷，提高了肥效模型的适用性和建模成功率。本研究在此基础上，根据植物营养元素功能不可相互替代的原理，构建二元非结构肥效模型，并进行田间试验验证，旨在提高二元肥效模型的适用性，为计量施肥和推荐施肥专家系统研发提供理论模型依据。

1 材料与方法

1.1 水稻二因素田间肥效试验设计

2017年分别在福建省永春县、平和县和大田县等水稻产区设置了氮磷、氮钾、磷钾二因素田间肥效试验，选择普通铁聚水耕人为土和普通简育水耕人为土等福建稻田主要土壤类型作为供试土壤。供试水稻均为当地大面积种植的杂交早稻和杂交单季稻良种。

每个试验实施前，按规范方法采集一个混合基础土样。用常规方法［21］测定供试土壤主要理化性状（表1），其中，pH为电位法，有机质为重铬酸钾容量法，碱解氮为碱解扩散法，有效磷（Olsen-P）为0.5 mol·L-1碳酸氢钠提取—钼锑抗比色法，速效钾为1 mol·L-1乙酸铵提取—火焰光度计测定法。

试验设计选用二因素五水平回归最优设计，共9个处理。其中，氮磷二因素试验的各处理为：（1）N0P0，（2）N0P1，（3）N1P0，（4）N1P1，（5）N0.25P0.25，（6）N0.25P0.75，（7）N0.75P0.25，（8）N0.75P0.75，（9）N0.5P0.5，氮钾、磷钾二因素试验的9个处理设计与此类似，下标为施肥量比例，处理（4）为试验设计的最高施肥量，各试验点最高施肥量见表1。

试验采用三次重复，随机区组排列，小区面积20 m2。试验所用氮肥选择尿素（N46%），磷肥选择过磷酸钙（P2O512%），钾肥用氯化钾（K2O 60%），试验地均不施有机肥。化肥分基肥和追肥施用，其中，磷肥全部做基肥施用；氮肥在基肥、分蘖肥和穗肥中各占总用量的50%、35%和15%；钾肥在基肥和穗肥中各占50%，分蘖期不施钾肥。供试水稻收获时，各小区单收单称，分别记录稻谷和稻草鲜重产量及其晒干产量。试验区四周保留1 m宽以上保护行。除施肥外，其他田间管理措施与大田生产一致。

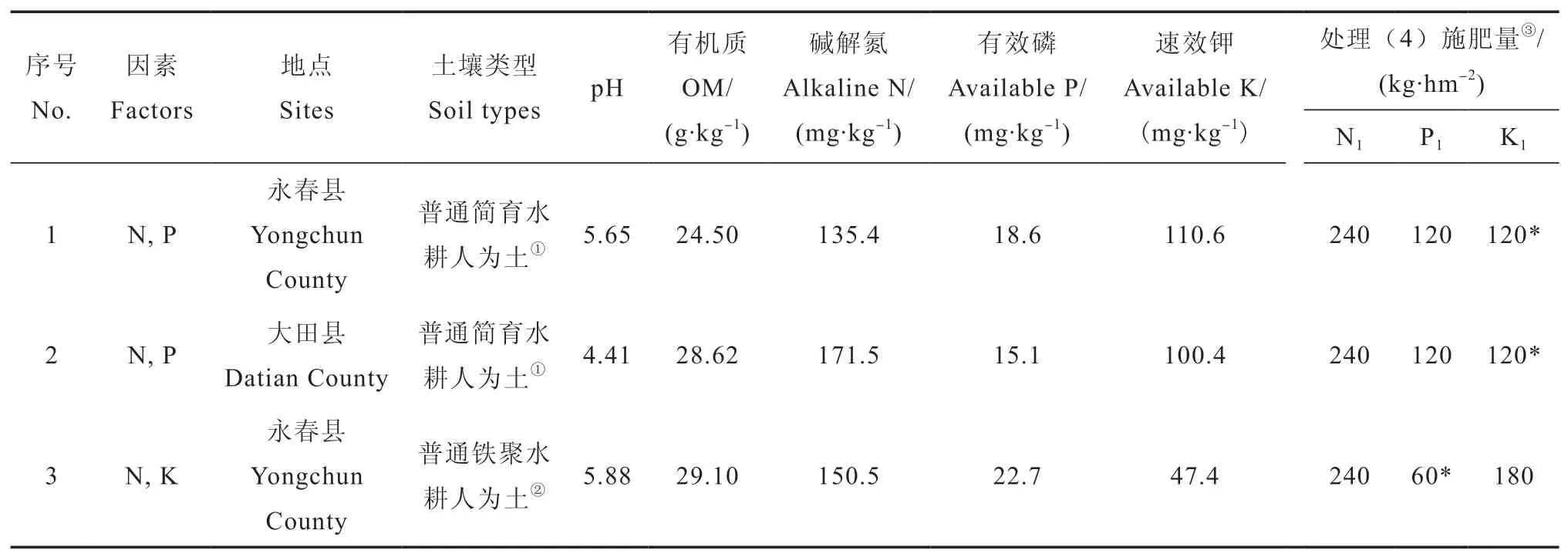
表1 水稻二元肥效试验供试土壤主要理化性状及其处理（4）施肥量Table 1 Main physical and chemical properties of the test soil in the experiments on rice and fertilizer application rate in the 4th treatment

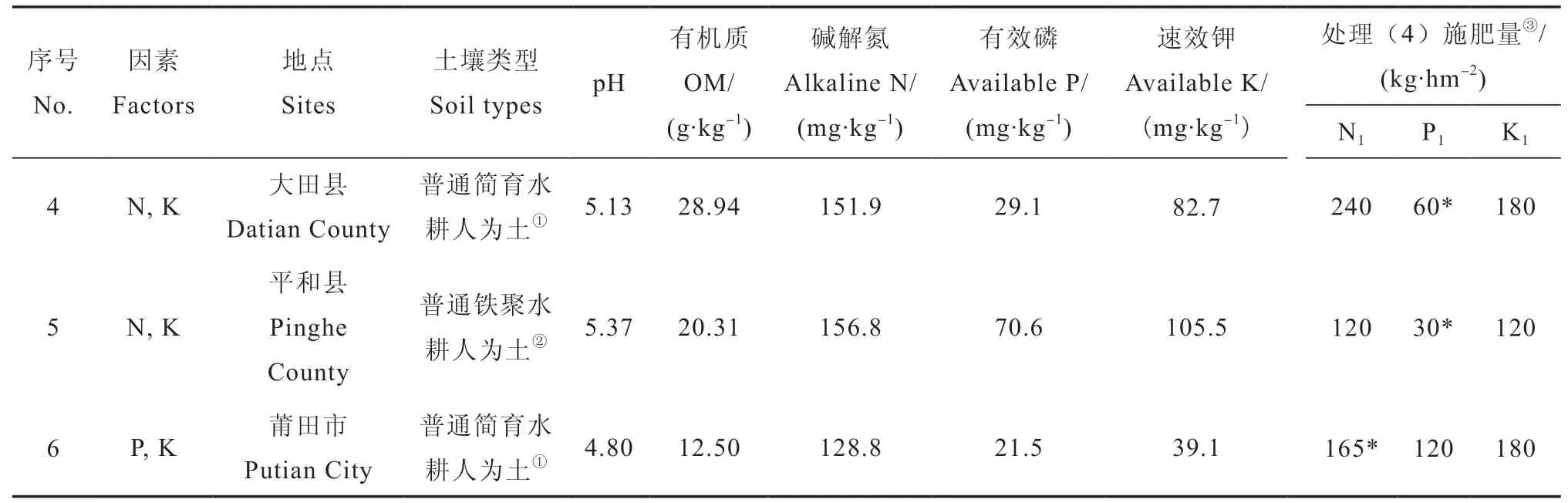
续表

1.2 旱作二因素田间肥效试验资料的收集整理

为了更全面地验证二元非结构肥效模型的适用性，本文引用作者在国际植物营养研究所合作项目中完成的7个氮、磷、钾的二因素田间肥效试验结果。试验的供试作物包括花生、马铃薯和毛豆等，试验内容、供试作物、设置地点、供试土壤类型和基础土样主要理化性状见表2。其中，1999年在莆田市秀屿区完成的花生磷钾肥效试验采用二因素重复D-饱和最优设计，共12个处理，其他6个试验均采用二因素3×3设计。田间试验方案和样品采集方法与水稻试验大致相同，不再赘述。此外，本研究引用李仁岗编著的《肥料效应函数》［22］在第20、22、102、126页提供的中国北方冬小麦和夏玉米的4个完整氮磷肥效试验资料，探讨新模型的建模效果，本文试验点编号分别为第14、15、16、17号。

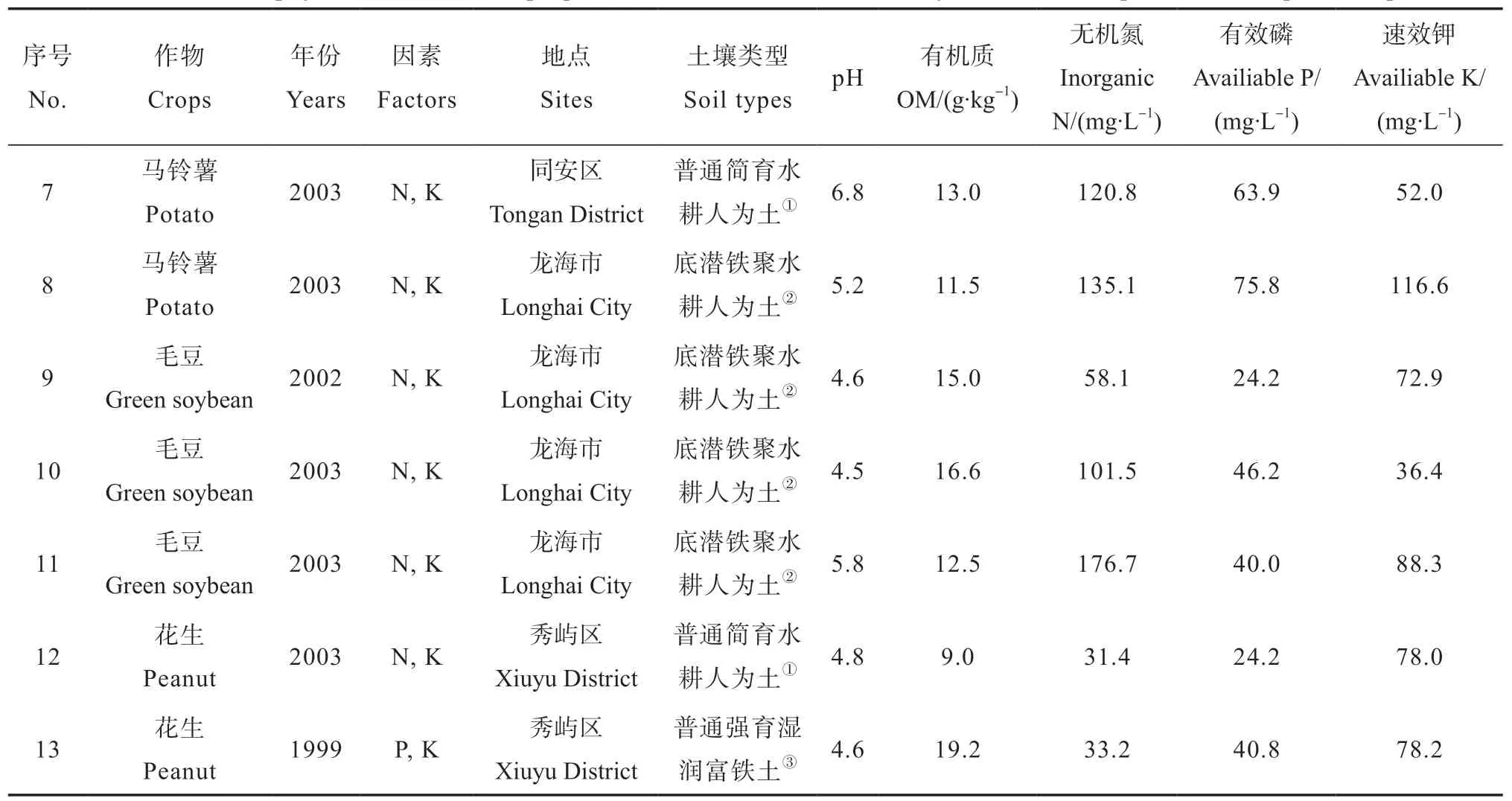
表2 旱作物二元肥效试验及其供试土壤主要理化性状1）Table 2 Main physical and chemical properties of the test soil in the binary fertilization experiments on upland crops

1.3 数据整理方法

二元二次多项式肥效模型采用普通最小二乘法回归建模，二元非结构肥效模型则采用非线性最小二乘法进行模型参数估计。在计算机上的具体实现则使用MATLABR2015b 软件的regress功能函数进行二元二次多项式肥效模型的回归建模，使用nlinfit功能函数进行二元非结构肥效模型参数估计和统计检验，具体数学原理和软件使用方法参见相关专著［23］。文中图形采用该软件编程绘制。

1.4 二元非结构肥效模型的构建

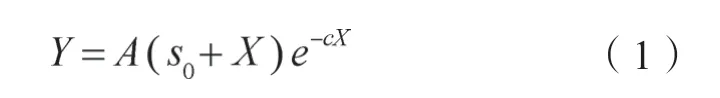
近年来，Zhang等［20］根据施用单位养分的稻谷增产量随施肥量的增加呈现指数规律下降的事实，构建了一元非结构肥效模型：式中，Y为稻谷产量，X为施肥量，s0为土壤供肥当量（即由土壤提供的相当于所施肥料的养分数量），单位均为kg·hm-2；c为施肥对产量的效应系数；A表示施肥量X=0时土壤肥力与稻谷产量之间的转换系数。

在式（1）的一元非结构肥效模型中，当施肥量和土壤供肥当量均为零时，作物产量必等于零。因此，根据植物营养元素功能不可相互替代的原理，二元非结构肥效模型可由两个一元非结构模型相乘而得，即：式中，s1、s2分别表示供试土壤氮磷钾中两种元素养分的供肥当量（kg·hm-2）。为使土壤当季养分供应当量与施肥量具有加和性，其值大小以N、P2O5、K2O养分形态计量；c1、c2分别表示两种养分元素的增产效应系数；A=A1×A2，表示两种养分施用量均为零时，土壤肥力与作物产量之间的转换系数，其他代数符号的含义与式（1）相同。

分析表明，式（2）模型在施肥量范围内存在一个产量峰值，该峰值对应的施肥量即为最高产量施肥量。因此，令式（2）的作物产量Y分别对X1、X2施肥量的导数等于零，得到最高产量施肥量计算式，令式（2）的作物产量Y分别对X1、X2施肥量的导数等于农产品和肥料价格倒数比，得到经济产量施肥量计算式，即：

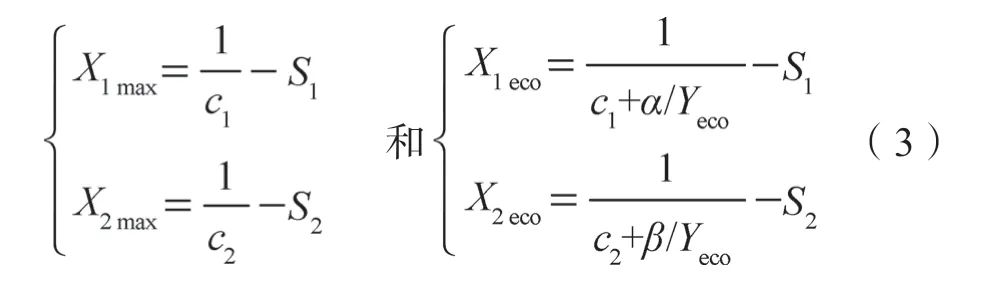
式中，α= PX1/PY，β =PX2/PY，PX1、PX2和PY分别表示每千克的X1、X2养分和农产品的市场价格。式中Yeco表示经济产量。经验表明，肥效模型计算所得最高产量和经济产量一般差异很小，Yeco可以用最高产量Ymax代替。也可以采用数学上的迭代算法得到经济施肥量的精确计算结果，一般迭代计算3～5次即可。

2 结 果

2.1 二元二次多项式肥效模型的田间试验资料拟合效果

水稻和旱作物的氮磷、氮钾和磷钾二因素田间肥效试验的施肥量及其产量结果见表3。利用常用的二元二次多项式肥效模型，即：对表3的水稻二元肥效试验结果，应用普通最小二乘法进行回归建模（表4），然后对各肥效模型进行典型性判别分析［23］。6个水稻二元二次多项式肥效模型的统计显著性指标F值和拟合优度R2等均达到显著水平。但是，仅有第6号早稻磷钾肥试验点建立的肥效模型属于典型式，可用于推荐施肥。在1号至5号试验点中，二元二次多项式肥效模型的一次项系数或二次项系数符号出现异常，不符合作物施肥效应的一般规律，肥效模型均属于系数符号不合理的非典型式。

对表3的第7号至13号试验点的马铃薯、毛豆和花生的7个二元肥效试验结果，以及冬小麦和夏玉米的4个氮磷二元肥效试验资料［22］，用相同方法回归建模和典型性判别（表4）。结果表明，在第7号至17号试验点的11个试验中，二元二次多项式肥效模型均能通过显著性检验，但第13号和第17号试验点建立的肥效模型均属于推荐施肥量外推的非典型式，丧失了推荐施肥的可靠性。

因此，在17个试验资料中，二元二次多项式典型肥效模型仅有10个，占试验点总数的58.8%，非典型肥效模型比例则占41.2%。

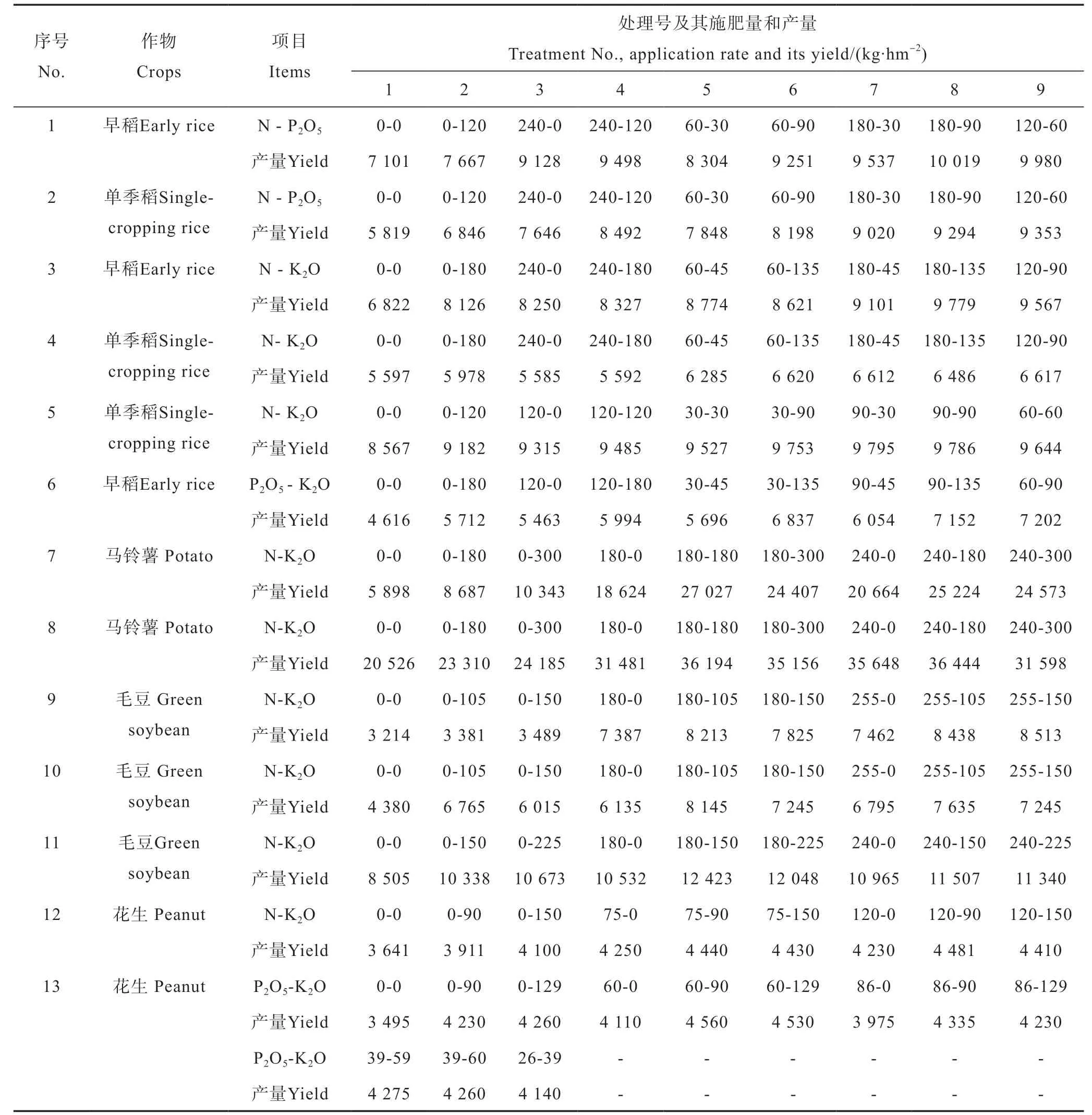
表3 水稻和旱作物氮磷、氮钾、磷钾二因素田间肥效试验施肥量和产量Table 3 Application rates and yields of rice and upland crops in the NP, NK and PK binary fertilizer experiments

2.2 二元非结构肥效模型的田间试验资料拟合效果

对式（2）的二元非结构肥效模型，应用表3的6个水稻肥效试验结果和非线性最小二乘法回归建模和典型性判别［22］。表5的1号至6号试验点结果显示，6个试验点的二元非结构肥效模型统计显著性指标F值和拟合优度R2同样均达到统计显著水平。与表4的相关指标相比，应用二元非结构肥效模型拟合这6个试验点的肥效试验结果，均能得到典型肥效模型，明显提高了田间试验的建模成功率。

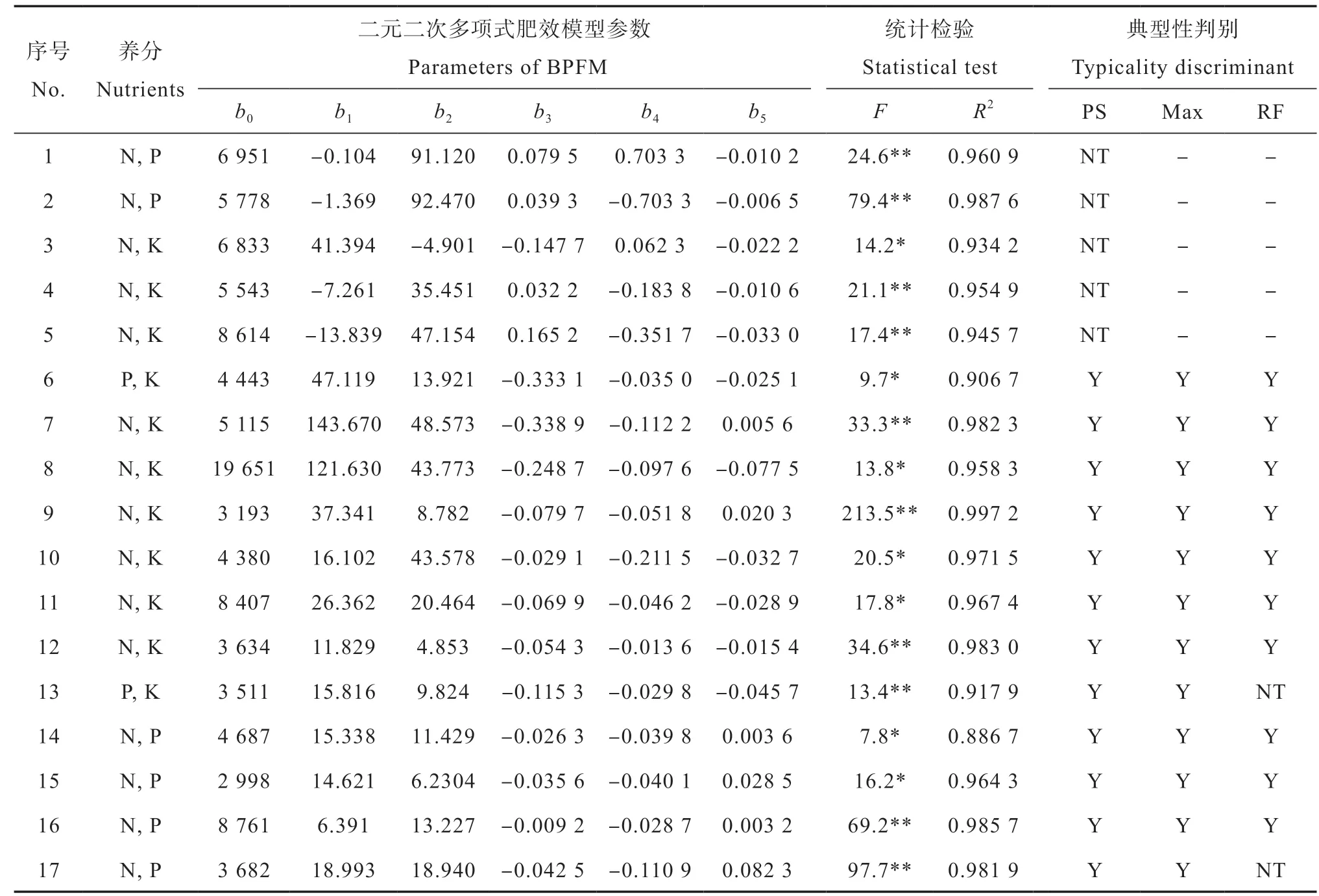
表4 二元二次多项式肥效模型对供试作物二元肥效试验资料的拟合效果Table 4 Fitting of crop responses with the binary quadratic polynomial fertilizer response model (BPFM) in the binary fertilization experiments

对表3的马铃薯、毛豆和花生的7个二元肥效试验结果，以及4个冬小麦和夏玉米氮磷二元肥效试验资料，应用相同方法建立二元非结构肥效模型，并进行典型性判别。表5的第7号至17号试验点的结果表明，尽管这11个试验当初是为建立二次多项式肥效模型而设计的典型肥效试验，二元二次多项式肥效模型能通过显著性检验或得到典型式的试验点，二元非结构肥效模型同样能够得到相同的建模结论；第13号和第17号试验点建立的二元非结构肥效模型与二元二次多项式模型一样，均属于推荐施肥量外推的非典型式。

因此，在1 7 个二元肥效试验结果中，二元非结构肥效模型的典型式有1 5个，占试验点总数的88.2%，非典型肥效模型比例仅占11.8%。新模型建模成功率较二次多项式肥效模型提高了2 9.4 个百分点，明显改善了肥效模型的适用性。

2.3 二元肥效模型推荐施肥量及其相关性

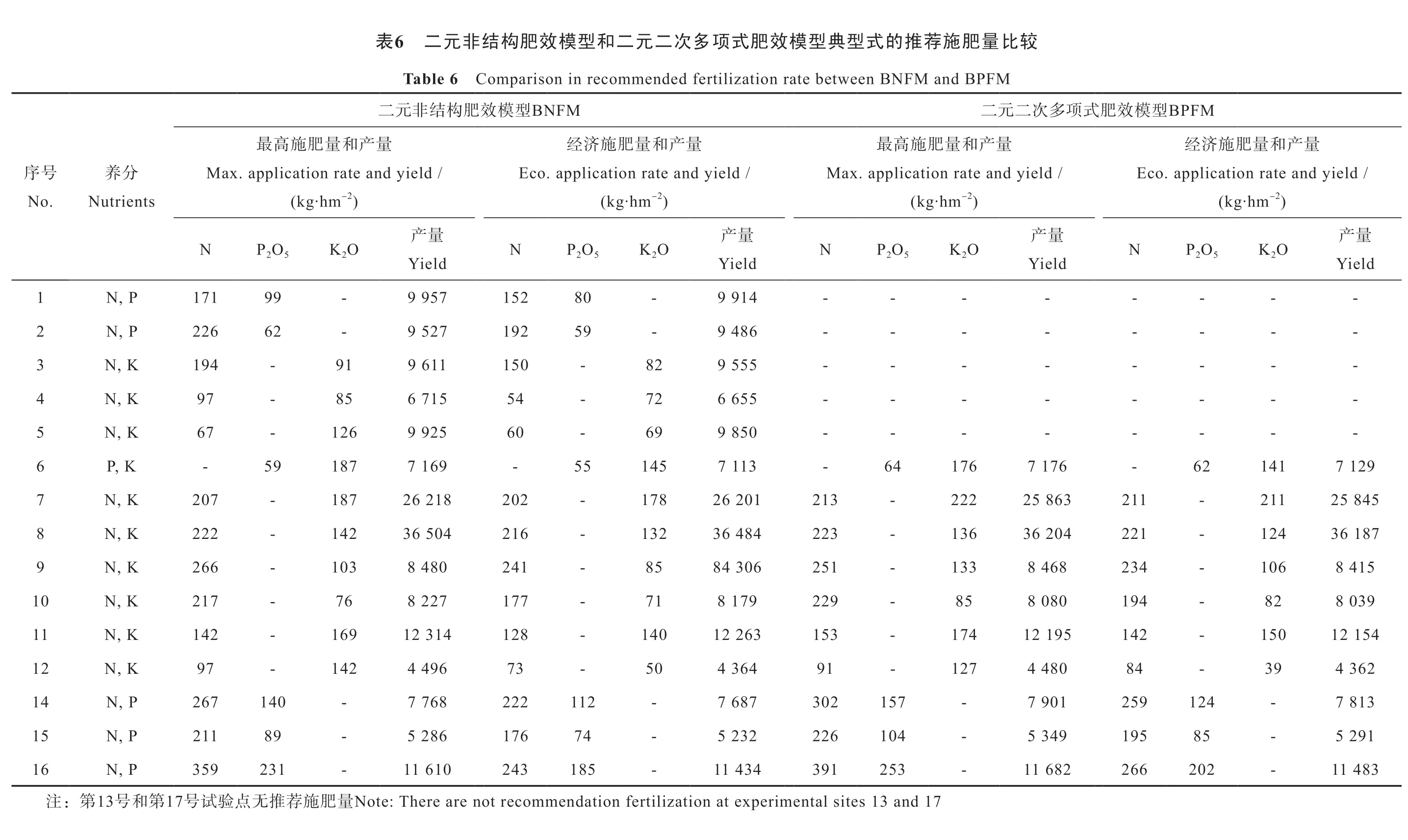
依据N4.3 yuan·kg-1、P2O55 yuan·kg-1、K2O 5 yuan·kg-1和农产品2 yuan·kg-1的市场均价，应用式（3）分别计算表5的典型二元非结构肥效模型相应试验点的推荐施肥量，同时，用边际产量导数法分别计算表4中典型二元二次多项式肥效模型试验点的推荐施肥（表6）。结果表明，典型二元非结构肥效模的最高施肥量和经济施肥量的推荐结果均在试验设计的施肥量范围内，未出现异常情况。

为比较两种模型在推荐施肥量上的差异，对表6中两种模型均能得到典型式的10个试验点得到的氮、磷、钾推荐施肥量绘制成图，并进行线性回归分析。表明两种模型推荐的最高施肥量之间以及经济施肥之间均存在极显著的线性正相关关系（图1）。回归方程的一次项系数分别仅有0.915 3和0.916 1，表明当二次多项式模型推荐的最高施肥量或经济施肥量每增加1 kg时，非结构肥效模型的相应推荐施肥分别仅增加0.915 3 kg和0.916 1 kg，较好地解决了二次多项式模型推荐施肥量普遍偏高的问题［1,11］。

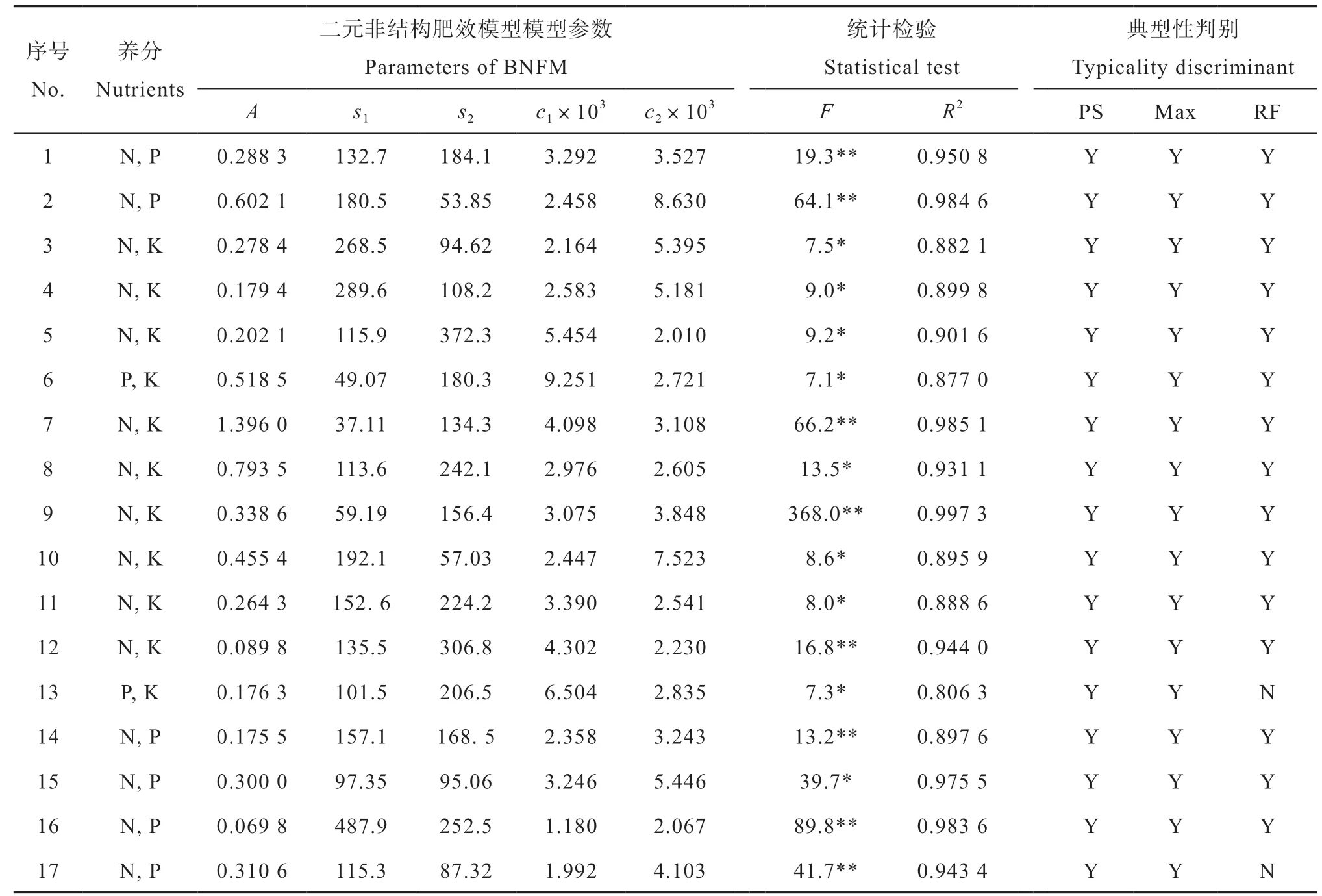
表5 二元非结构肥效模型对供试作物二元肥效试验资料的拟合效果Table 5 Fitting of crop responses with the binary non-structural fertilizer response model (BNFM) in the binary fertilization experiments

3 讨 论

3.1 二元二次多项式肥效模型的局限性

肥料效应函数法是我国测土配方施肥技术的一个重要分支体系。在过去四十年里，在多项式肥效模型选择及其适用性、试验设计与参数估计方法、类特征肥效模型构建方法以及非典型式推荐施肥优化方法等方面的研究和应用取得重要进展［1-2］。但不可否认的是，该法对田间肥效试验结果的建模成功率明显偏低，并且长期未能得到有效解决，以至于不少人对肥效模型的实用价值丧失信心。本研究在水稻田间试验实施前，作者曾考虑到试验目的是希望得到反映施肥量与水稻产量关系全貌的肥效函数曲面，因而，试验设计选用二因素五水平回归设计。虽然该设计在理论上具有5个施肥水平，且各施肥水平均匀分布在试验施肥量范围内，有利于控制效应曲面的形状，但是，试验结果用于建立二元二次多项式肥效模型的效果仍然不理想，在6个试验中仅有一个试验点能得到典型肥效模型。究其原因，肥效模型设定本身的合理性和可靠性这个核心问题长期未被触及，更鲜见提出改进建议。

MFPB型模效量产和量肥施济经/ dleiy dna etar noitacilppa .ocE 2-)mh·gk(量产O K OP N 2 5 2 dleiY--------------------921 7 141 26-548 52 112-112 781 63 421-122 514 8 601-432 930 8 28-491 451 21 051-241 263 4 93-48 318 7-421 952 192 5-58 591 384 11-202 662肥式6较比量肥施荐推的式型典型模效肥式项多次二元二和型模效肥构结非元二表MFPB dna MFNB neewteb etar noitazilitref dednemmocer ni nosirapmoC6 elbaT项多次二元二MFNB型模效肥构结非元二量产和量肥施高最量产和量肥施济经量产和量肥施高最/ dleiy dna etar noitacilppa .xaM/ dleiy dna etar noitacilppa .ocE/ dleiy dna etar noitacilppa .xaM 222---)mh·gk()mh·gk()mh·gk(量产量产量产O K OP N O K OP N O K OP N 2 5 2 2 5 2 2 5 2 dleiY dleiY dleiY----419 9-08 251 759 9-99 171----684 9-95 291 725 9-26 622----555 9 28-051 116 9 19-491----556 6 27-45 517 6 58-79----058 9 96-06 529 9 621-76 671 7 671 46-311 7 541 55-961 7 781 95-368 52 222-312 102 62 871-202 812 62 781-702 402 63 631-322 484 63 231-612 405 63 241-222 864 8 331-152 603 48 58-142 084 8 301-662 080 8 58-922 971 8 17-771 722 8 67-712 591 21 471-351 362 21 041-821 413 21 961-241 084 4 721-19 463 4 05-37 694 4 241-79 109 7-751 203 786 7-211 222 867 7-041 762 943 5-401 622 232 5-47 671 682 5-98 112 286 11-352 193 434 11-581 342 016 11-132 953 71 dna 31 setis latnemirepxe ta noitazilitref noitadnemmocer ton era erehT :etoN 71量肥施荐推无点验试号分养stneirtuN P ,N P ,N K ,N K ,N K ,N K ,P K ,N K ,N K ,N K ,N K ,N K ,N P ,N P ,N P ,N31第和号第号序.oN123456789011121415161：注

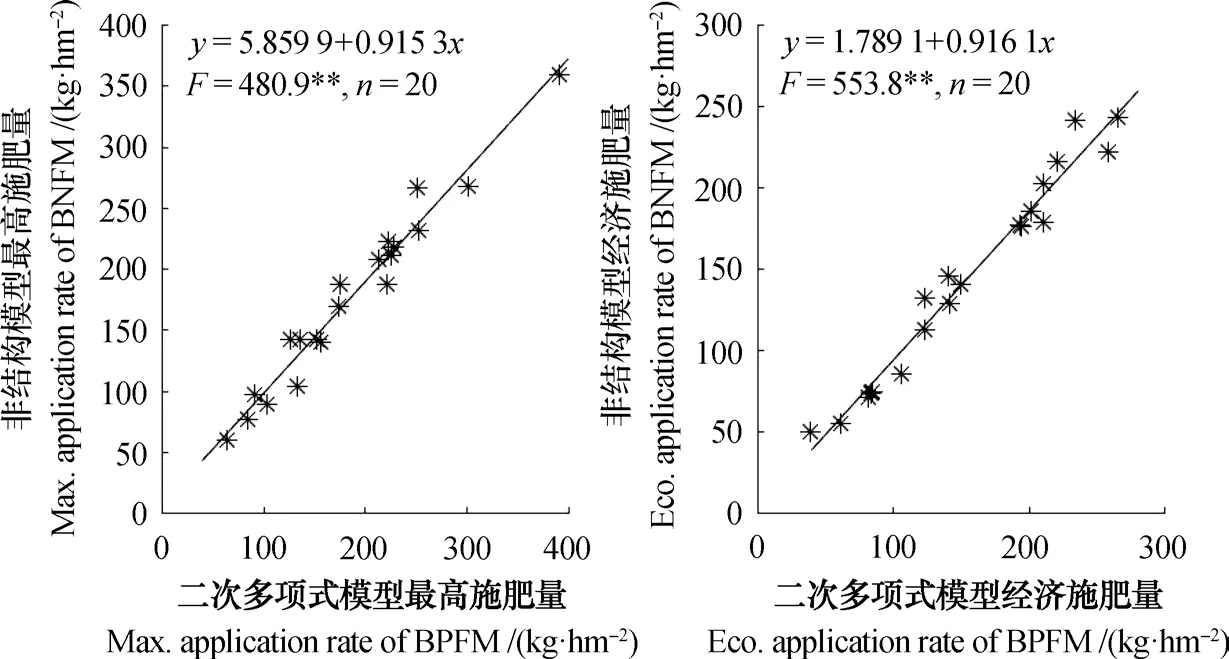
图1 二元非结构肥效模型与二元二次多项式肥效模型推荐施肥量的相关性Fig. 1 Relationship in recommendation fertilization rate between the binary non-structural fertilizer response model (BNFM) and the binary quadratic polynomial fertilizer response model (BPFM)

作者曾对当前广泛使用的经验肥效模型的研究和应用进展进行过总结，发现常用的二次多项式肥效模型存在不符合生产实际的两个缺陷［2］，即：单位养分增产量与施肥量之间的函数关系采用线性模型，导致最高施肥量之前施肥的增产效应与最高施肥量之后施肥的减产效应是对称关系，忽略了当前广泛推广应用的高产耐肥新品种在过量施肥时，产量降低幅度得到较大程度缓解的肥料效应特征，同时，也忽略了土壤对养分的缓冲能力，进而减轻过量施肥对作物产量负效应的作用；其次是二次多项式肥效模型的回归变量间存在强烈的多重共线性［18］和异方差［19］，严重制约了普通最小二乘法回归建模的有效性和统计检验结果的可靠性。因此，模型设定偏误、多重共线性和异方差等因素是导致二次多项式肥效模型建模成功率偏低的重要原因。

3.2 二元非结构肥效模型的适用性

针对多项式统计模型的多重共线性和异方差等问题，现代数理统计学已提出了诸多解决办法［17］。研究表明，主成分回归建模法在克服多重共线性危害［18］、广义可行最小二乘回归建模法在克服异方差危害［19］等方面具有实用价值。但是，这些方法并不能克服模型设定偏误问题，而且，二次多项式肥效模型往往同时存在多重共线性和异方差，如何同时解决这两个问题，目前在统计学上还难以做到。因此，研发新的肥效模型就成为解决相关问题的关键。

本研究在一元非结构肥效模型［20］的基础上，根据植物营养元素功能不可相互替代的原理，建立了式（2）模型。该模型在数学形式上显然不同于二元二次多项式肥效模型，也不同于根系养分吸收机理模型［24］，但模型中的各参数具有明确的肥效含义，应用上也较为简便。借鉴种群生态学对不同类型模型的命名方法［25-26］，将这种介于经验模型和机理模型之间的式（2）模型称为二元非结构肥效模型。新模型较好地克服了二次多项式模型在施肥效应中的对称缺陷，同时，不能直接进行线性化转换，较好地克服了困扰二次多项式肥效模型的多重共线性等问题，是新模型建模成功率明显改善（表5）的主要原因。在推荐施肥量方面，两种模型均能应用到典型肥效模型的试验点，推荐的最高施肥量之间以及经济施肥之间均存在极显著的线性正相关关系，而且新模型的推荐施肥量普遍较低，较好地克服了二次多项式模型推荐施肥量普遍偏高的问题［1,11］。

理论分析表明，对式（2）二元非结构肥效模型的ex项进行泰勒级数展开，即：ex=1+x+G(x),x∈(-∞, +∞)，其中，因式（2）模型的c值在10-3次方级（表5），若仅取前两项，且忽略X1X2的高次项，并令B=(1+c1s1)，C=(1+c2s2)；则式（2）模型可转化为：Y=A结果与二元二次多项式肥效模型具有相同的数学表达式。可见，二元二次多项式肥效模型是二元非结构肥效模型的简化式。当某些试验点的肥效试验结果能够使剩余量G(x)达到足够小时，这两种模型均可能得到很好的拟合效果。表5的建模结果表明，二元二次多项式肥效模型能得到典型式的试验资料，二元非结构肥效模型同样能得到典型肥效模型。但当剩余量G(x)较大时，二元二次多项式肥效模型可能会因过度简化导致拟合效果欠佳，而非结构肥效模型因未进行这种简化而可能仍然具有较好的拟合效果。因此，二元非结构肥效模型具有更宽的适用范围。

4 结 论

模型设定偏误、多重共线性和异方差等问题是导致二元二次多项式肥效模型建模成功率偏低的主要原因，二元非结构肥效模型较好地克服了这些已知局限性，具有更高的拟合精度和更宽的适用范围。