双层悬栅消能率影响因素排序及布置形式研究

贾萍阳，牧振伟，蒋健楠

（1．新疆农业大学水利与土木工程学院，新疆 乌鲁木齐830052；2．江苏省水利勘测设计研究院有限公司，江苏扬州225127）

在同等水力条件下，消力池中布置双层悬栅比布置单层悬栅消能率更高［1］，但双层悬栅的布置参数较单层悬栅多，消能率影响因素增多。双层悬栅的栅条数、栅距、层距是影响消力池消能效果的主要布置参数。由于影响因素多，参数设置有多种组合方案，从而增大了试验量，增加了试验难度，且悬栅因子对于消能率影响呈非正态、非线性分布［2］，因此对于这种多因素、多水平的模型试验采用常规的线性回归方法很难建立其数值模型［3-5］。投影寻踪回归技术（PPR）经过多年的实践与升级［6-10］被证明模拟效果较好，接近客观规律。黄浩等［11］采用投影寻踪回归统计方法，获得了河型影响因素的相对贡献权重值及河型变化规律，通过实例检测证明了PPR技术有效可靠。柏承宇［12］将投影寻踪回归技术应用于电力负荷预测中，结果显示，投影寻踪回归技术可以较好地模拟城市用电量的规律，具有很好的应用前景。李启月等［13］通过对比BP神经网络和投影寻踪回归对光面爆破炮孔利用率的试验成果，发现投影寻踪回归技术更接近实际。吴思等［14］利用投影寻踪回归分析得出影响人工渠道糙率系数的主要影响因素为弗劳德数Fr。但此前少有投影寻踪回归技术针对消力池内双层悬栅消能率进行研究。蒋健楠等［15］已通过模型试验测量得出消力池内布置双层悬栅较未布置悬栅消能率更高，但其对悬栅布置参数与消能率之间的关系尚未研究。笔者在此基础上，利用消力池内双层悬栅模型试验结合PPR技术，研究双层悬栅消能率影响因素排序及建立其PPR数学模型，并得到了消力池中双层悬栅最佳布置型式。

1 物理模型试验设计

1．1 物理模型设计

试验模型如图1所示。模型由水箱、进口引水段、消力池、出口泄水段及量水堰构成，总长约9．3 m。其中消力池前引水段坡比为0．001 5，消力池长120 cm，池宽18 cm，池深d为10 cm，边墙高39．5 cm；悬栅采用矩形栅条，长18 cm，宽1 cm，高2 cm。其中渥奇段布置4根悬栅，此处悬栅高度距离底板均为7 cm；渐变段悬栅栅高h为8．5 cm，水平间距为3．5 cm；消力池内上层悬栅与池底的距离h1为11 cm，下层悬栅与池底的距离h2为7 cm，两层悬栅之间间距b2为4 cm，为便于调整悬栅布置形式，消力池内悬栅采用M形布置。试验时渥奇段及渐变段悬栅为固定条件，只改变消力池内悬栅布置形式。

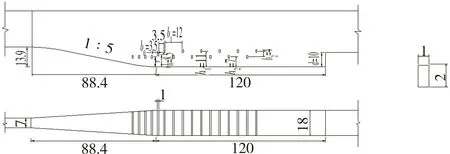
图1 悬栅消力池结构尺寸（单位：cm）

1．2 消能率计算方法

断面水深采用测针测量，测针测量精度为0．1 mm，取断面水位最高处读数与该断面底部读数之差为该断面水深H。流量的测量采用三角形量水堰。消能率计算公式为

其中

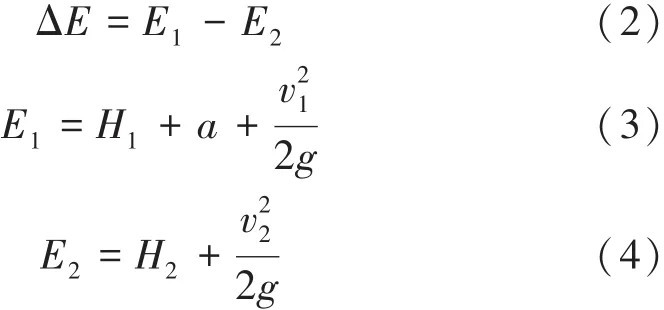
式中：H1、H2分别为来流、出流断面水深，cm；v1、v2分别为来流、出流断面平均流速，cm／s；E1、E2分别为来流、出流断面的能量；ΔE为消力池消耗的能量；a为来流、出流水位差，模型中a＝13．8 cm。

1．3 试验方案设计

试验设定悬栅栅距（cm）、悬栅层距（cm）、悬栅条数（根）3个因素，将每个因素分成5级水平，每组试验只变动一个因素，其他两个因素保持在中水平。共设计15组双层悬栅消能工布置方案，分别在15 000 cm3／s和 13 000 cm3／s两种流量条件下进行试验，具体方案见表1。

表1 悬栅布置方案

2 双层悬栅影响因素排序

2．1 物理模型试验结果分析

极差分析可以直观地反映试验因素对试验结果影响的显著性，极差大说明该因素对试验结果影响显著，为主要因素，反之为次要因素。通过计算模型试验的水力参数，得到在15 000 cm3／s流量条件下的消能率与极差，见表2。只变动层距这一因子时，最大消能率为76．83%，最小消能率为 75．62%，层距的极差为1．21%（最大消能率减去最小消能率），依次计算得出栅距极差为0．72%、栅条数极差为0．97%，极差大小排序为层距、栅条数、栅距。

表2 设计流量与验证流量下消能率与极差

为了增强试验结果的可靠性，在13 000 cm3／s流量条件下重复试验，得到验证流量下极差大小的排序依然是层距、栅条数、栅距。

从试验结果来看，对消能率影响最大的因素是层距，其次是栅条数，栅距对消能率的影响最小。这说明双层悬栅消力池中对水流起到消波稳流作用的主要因素是层距。水流通过悬栅会形成一种特有的绕栅旋涡（见图2），上层悬栅与下层悬栅所形成的旋涡彼此之间相互影响，两股旋涡充分摩擦、剪切，这个过程消耗了大量的水流能量。层距的大小直接影响上下两股旋涡的交互，层距越大，上下旋涡所形成的流场相隔越远，接触摩擦越小。同时上层悬栅与下层悬栅的净间距决定悬栅的相对阻水面积，因此层距对消能率的影响最显著，且适当的层距可以产生理想的消能效果。对消能率影响较为显著的因素是栅条数，栅条数越多，消力池中产生的绕栅旋涡越多，水流因旋涡而消耗的能量越大。栅距对消能率的影响最小，前排悬栅迎拒的水流能量最强，旋涡范围最大，后排悬栅由于池中水流能量沿程下降，所形成的旋涡范围逐渐减小，因此同一层中相邻悬栅的旋涡交互作用不大，对消能率的影响较小。综上所述，双层悬栅消能率影响因素显著性的排序是层距、栅条数、栅距。

图2 消力池内绕栅旋涡数值模拟

2．2 PPR 建模分析

PPR可以进行自然界客观事物规律模拟，对于复杂的水力学模型问题，PPR能快速而简便地从试验数据中寻求客观规律，进行模拟，减少物理试验次数，提高试验效率，避免人工求解非正态、非线性公式，摆脱量纲的束缚，在无人为假定的情况下寻找变量与结果的客观规律。PPR基本思路是将高维数据投影到低维子空间上，改变投影方向，找出能反映高维数据结构和特征的投影图形，再以数值函数来逼近拟合，给出高维数据各个因子的影响作用，便于定性分析其客观规律。设y为消能率，x为变动因子，PPR模型公式为

式中：¯y为试验消能率平均值；MU为数值函数最优个数；βi为数值函数的贡献权重系数；fi为数值函数；ai为i方向的投影值，‖αi‖＝1，i＝1，2，…，MU。

将表2中15组验证流量试验数据导入PPR中建模拟合。参数设置：光滑系数S取0．1（默认值为0．5，值越小，拟合精度越高）；N表示数据组数，共15组试验数据；P为自变量个数，设栅距、层距、栅条数作为自变量，共3个；Q表示目标函数个数，本文目标函数只有消能率，Q取1；投影方向初始值M取5，最终投影方向MU设为3。双层悬栅消能率的PPR数学拟合值、物理模型实测值及误差统计见表3，可见拟合值与实测值十分接近，且15组试验数据的拟合合格率均达到100%，说明PPR建模可以较好地模拟双层悬栅影响因素与消能率之间的规律。根据PPR物理模型数据，双层悬栅消能率影响因素层距、栅距、栅条数的权重值分别为 1．000、0．726、0．807（见表 4），即权重值的大小排序为层距、栅条数、栅距，这与模型试验极差分析双层悬栅消能率得出的结果一致，说明PPR建立的数学模型可靠。PPR在Excel中建立的数值计算模型可以直接作为双层悬栅消能工计算公式，即在Excel中赋予层距、栅距、栅条数参数具体值，可得到对应方案的消能率。

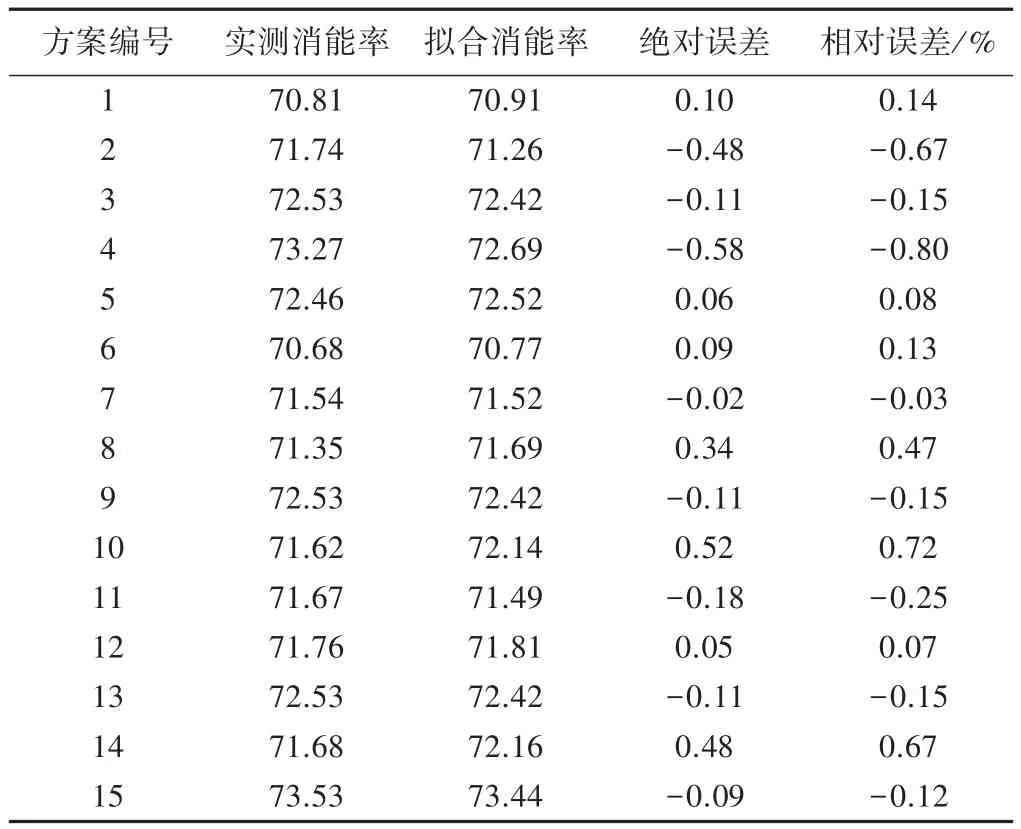
表3 PPR模型拟合结果与物理模型数据对比 %

表4 双层悬栅消能率影响因素权重值

3 双层悬栅布置形式研究

根据悬栅影响因素排序分析，消力池内布设的悬栅根数越多，水流产生的绕栅旋涡越多，消能率越高。但对于该试验模型来说，消力池长度只有120 cm，受消力池长度的限制，悬栅根数的布设同样受到约束。在有限长度的条件下，综合蒋健楠等［16］的试验结论，消力池中布设11根悬栅时最大水深下降幅度最大，所以消力池中悬栅根数定为11根。在消力池内加置11根悬栅的条件下寻找最佳层距与栅距组合。根据表2中试验数据，绘制 15 000 cm3／s与 13 000 cm3／s流量下变动因子与消能率关系图（见图3）。

图3 变动因子与消能率的关系

由图3（a）可以看出：在流量 15 000 cm3／s条件下，保持悬栅根数与栅距不变，只改变层距，层距（为2～5 cm时）越大消能率越高，当层距为5 cm时，消能率达到最大值76．83%，之后随着层距的增大，消能率呈现下降趋势。在流量13 000 cm3／s下，消能率与层距的关系呈现出与流量15 000 cm3／s相似的变化趋势，先上升后下降，当层距为5 cm时，消能率达最大值73．27%。两种流量条件下，层距的改变对于消能率的影响均表现出同样的变化规律，层距（小于5 cm时）越大，消能率越高，上下两股旋涡充分摩擦；当层距为5 cm时，两股旋涡可以最大程度耗散水动能，此时消能率达到最大；当层距大于5 cm时，上下两股绕栅旋涡逐渐远离，消能率降低。

根据图 3（b）可知：在流量 15 000 cm3／s下，当栅距小于12 cm时消能率随着栅距的增大而升高；当栅距为12 cm时，消能率达到最大值75．62%，之后随着栅距的增大而下降。在流量13 000 cm3／s下，随着栅距的增大，消能率同样先上升后下降，在栅距为12 cm时达最大值。

两种流量条件下，栅距的变化对消能率的影响规律相同。层距达到5 cm时即出现消能率峰值，而栅距增大到12 cm时消能率才出现峰值，同样印证前面讨论的层距对消能率的敏感性高于栅距，说明每根悬栅形成的旋涡呈椭圆形，与数值模拟呈现的图像（见图2）吻合。栅距的变化表现为前后旋涡相互影响，当栅距为12 cm时，前后悬栅形成的绕栅旋涡充分摩擦，消耗大量水能；当栅距大于12 cm时，两股旋涡交互影响逐渐弱化。

综上所述，当悬栅数目保持11根、层距为5 cm、栅距为12 cm时，消能率最高，水跃前移，出流平稳，池内流态较好。

4 结 论

（1）模型试验极差分析与PPR数值模拟均得出双层悬栅消能率影响因素的显著性排序为层距、栅条数、栅距，说明层距是影响消能率的关键因素。

（2）PPR在Excel中建立的数值计算模型文件可以保存留用。当Excel中赋予层距、栅距、栅条数参数具体值时，能得到对应方案的消能率，较模型试验观测更快捷。

（3）在下泄流量为 15 000 cm3／s 与 13 000 cm3／s情况下，消力池中栅条数为11根、层距为5 cm、栅距为12 cm时，池中消能率最高，消能效果较好，为双层悬栅最佳布置形式。