点云初始配准的优化求解算法

沈江华,孙殿柱,李延瑞,梁增凯

(1.山东理工大学机械工程学院,255049,山东淄博; 2.西安交通大学机械工程学院,710049,西安)

逆向工程中,物体的表面采样数据一般用于其三维模型重构,故要求实际采样数据必须是完整的。然而,在实际测量过程中,由于受被测物体几何形状及扫描设备的测量范围限制,需要从不同视角对物体进行多次测量,测量结果是多片具有部分重叠区域的局部点云数据,不能为三维重构系统所接受,因而必须采用三维点云配准[1]技术将不同视角下的多片局部点云统一到同一坐标系中以获得完整的物体表面点云数据。点云配准精度直接决定了点云数据反映物体表面特征信息的完整性、准确性,对点云数据的三维重构精度有重要影响。在质量检测、计算机视觉、逆向工程等领域,点云配准技术均有广泛应用[2]。

迭代最近点算法[3](ICP)是一种基于对应点的配准算法,以欧氏距离最小的点作为对应点,通过最小化两个点集中的对应点距离平方和得到两个三维数据集之间的刚性变换。为提高配准中两组点云对应点匹配的正确率,通常需要加入采样点的法矢、曲率等局部几何特征[4-9]。Rusu等提出一种快速点特征直方图(FPFH),用以描述点云数据集中任一采样点邻域的局部几何信息,该算法采用样本一致性方法对初始FPFH特征点进行采样,对于符合要求的特征点予以保留并用于后续配准[6]。Guo等提取深度图像的旋转投影统计(RoSP)特征,根据特征匹配后的对应点使用变换估计方法进行配准[7]。徐思雨等基于裁剪ICP算法对基于特征点匹配的配准结果进行修正,获得了更高的配准精度[8]。孙殿柱等对曲面局部采样点构建泊松曲面,以点-泊松曲面代替点-点作为匹配规则,以采样点在泊松曲面内的最近点作为匹配点,提高了配准过程收敛于全局最优的稳定性[9]。

与ICP算法相比,文献[4-9]算法在一定程度上提高了配准精度,但是由于需要求解采样点法矢、曲率等几何信息,使算法复杂化,无法兼顾配准精度和效率,并且同样对配准初始值较为敏感。为了获得配准初始值,Jung等由点云数据生成多幅深度图像,用二维深度图像配准实现三维点云的初始配准,降低了ICP算法陷入局部最小值的风险[10]。Chanki等将配准问题转化为混合整数线性规划的分支定界问题,所提出的算法[11]能够从两组数据之间的三维特征的假定匹配中找到正确匹配的最大数量,并且以全局最优方式估计变换参数,结果更准确可靠,但是计算效率较低。为了提高配准效率,一些学者利用相机拍摄的场景图像对三维扫描仪的运动轨迹进行跟踪,从而实现点云精确配准[12-13]。Al-Manasir等将相机以任意位置固定在激光扫描仪,因此必须对相机和激光扫描仪坐标系之间的关系进行标定,并且需要根据图像可识别扫描点的对应坐标计算真实的平移变换[12]。王瑞岩等利用计算机视觉的对极几何知识,直接求解相机的相对旋转变换[13],提高了算法的稳健性,但只能用于相机与扫描设备同轴的场合,且对于多视角点云,用该算法计算的旋转变换会存在累积误差。

由于ICP算法具有易于实现且配准精度高的特点,因此将其应用于存在较大重叠区域的点云配准问题的求解是非常合理的,但是ICP算法是基于点的欧氏距离寻找对应点的方法,匹配结果受点云间相对位置影响较大。当点云相对位置相差较大时,极易出现错误匹配,并且配准过程未进一步从匹配结果中筛选出正确的匹配,易导致迭代次数增加,降低配准效率,甚至使配准过程收敛于不理想的局部最优解。

针对上述问题,本文基于增量式运动法重建思想,提出一种结合图像信息的点云初始配准算法,引入相机坐标系,间接建立点云数据间的几何位置关系。在配准过程中,先将三维数据集中空间点与空间点的匹配转化为二维图像集中特征点与特征点的匹配,缩小同名点的匹配范围,然后利用图像对极几何约束重建特征点,恢复待配准点云的初始运动参数并进行优化,进而将初始配准后新的位置作为精确配准迭代过程的初始值,保证ICP算法的配准精度。实验结果表明,基于图像信息的点云初始配准算法对初始位置无严格要求,可使配准过程在初始位置相差较大情况下收敛的稳定性更高,并且在保证配准精度的同时提高了配准过程的收敛速度。

1 增量式稀疏重建

增量式稀疏重建可从不同视角拍摄的图像序列获得所拍摄物体的三维模型[14]。在序列图像重建阶段根据采集的二维场景图信息,计算相机在不同位置拍摄图像时的外参数。设相机在不同拍摄位置的外参数为集合Φ={Mi|i=1,2,…,NC},其中,外参数Mi为3×4维矩阵,NC为图像总数,序列图像经重建所得的物体三维结构记为点集Ω={S(k)|k=1,2,…,NC-1},其中S(k)表示第k次重建新增加的空间点集。

设序列图像为Σ={Ii|i=1,2,…,NC},应用尺度不变特征变换(SIFT)算法[15]检测Σ特征点,并根据对应特征点的特征描述符之间欧氏距离最小原则以及对极几何约束,对图像集Σ中任意相邻两幅图像依次进行特征点匹配,并将特征点匹配结果记为集合Ψ={Ii,i+1|i=1,2,…,NC-1},其中,Ii,i+1表示图像Ii与Ii+1的特征点匹配对集合。增量式稀疏重建是一个迭代计算的过程,首先通过I1和I2的特征点匹配对集合I1,2对模型进行初始化处理,并将重建所得的物体三维结构X(1)、相机外参数M1和M2作为重建阶段的基础;然后每增加一幅图像Ii,就利用Ii已重建的特征点图像坐标与对应的空间坐标解决透视点n的定位问题[16],求解出相机外参数Mi,进而通过三角测量将新图像Ii重建到当前模型Ω中,新扩展的点集为S(i-1)。迭代计算过程中,利用光束法平差[17]非线性优化相机外参数和点坐标,使总误差最小化,避免因相机外参数以及点坐标的误差累积而造成重建结果失真。

如图1所示,增量式稀疏重建算法根据图像Ii、Ii+1特征点信息估计相机外参数Mi、Mi+1,计算结果的准确性依赖于正确的图像特征点匹配对数量,而ICP算法是一种仅利用点云数据自身的三维坐标信息计算待配准点云Q、P之间的变换矩阵R、t,从而实现局部坐标系统一的迭代计算方法。

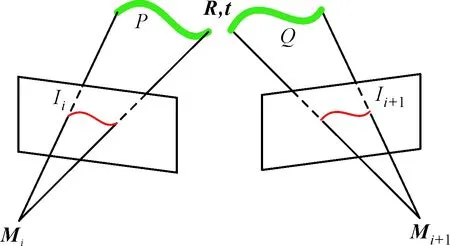
图1 相机定位与ICP配准示意图

ICP算法在目标点云Q中搜索源点云P中任一采样点的最近点时遵循欧氏距离最小原则,对于具有较高重叠度的Q、P,不可避免地存在错误对应点,当采用奇异值分解法(SVD)求解变换矩阵时,由于错误对应点被代入目标函数,计算结果会包含误差。当点云初始位置相差较大时,ICP收敛方向不确定,配准结果也不可靠。由此可知,多视角点云数据配准问题的关键在于不同视角下对应点集的选取,而较好的点云初始位置是基于距离特征进行准确选取对应点集的前提。因此,对于部分重叠的点云,为保证其配准结果的正确性,ICP算法需要较好的初始配准参数。

鉴于现有图像特征点检测与匹配算法能快速获取序列重叠图像的对应特征点,若能将点云从其局部坐标系变换到相机坐标系,便可通过增量式稀疏重建求解变换矩阵,实现点云初始配准。重建过程中不仅会对特征点匹配对进行初次筛选,而且通过光束法平差以全局最优方式估计变换矩阵。

2 相机坐标系下的点云表示

测量物体表面数据时,三维光学扫描仪中的相机与光栅投影装置的相对位置始终保持不变,则相机与光栅投影装置之间存在一个未知且固定的刚性变换。如图2所示,设由扫描仪测量获得的点云所在局部坐标系为oW-xWyWzW,其相机坐标系为oC-xCyCzC,这两个坐标系之间的刚性变换关系记为旋转变换RW和平移变换tW,此刚性变换可通过基于标定物的标定方法求解[12],其理论依据是透视投影原理。若空间中任意一点在两个坐标系中的坐标分别为XW和XC,则采用式(1)可将局部坐标系下的坐标转换到相机坐标系

XC=RWXW+tW

(1)

图2 相机坐标系定位原理图

3 序列图像的相对定位

在对物体进行全方位测量时,需要从多个视角测量物体的各个侧面和局部。通常情况下,三维测量装置的运动信息是未知的,在无任何先验知识的情况下直接获取点云配准参数是较困难的,而将局部坐标系下的点云数据转换到相机坐标系,便可将点云配准问题转化为序列图像定位问题,即估计各站点相机外参数。

相机外参数估计问题,是计算机视觉领域的研究重点,利用三维稀疏重建技术重建序列图像,在恢复场景结构的同时能得到相机外参数。另外,点云配准过程中相机外参数估计问题属于小规模图像的重建问题,计算量小。因此,本文基于增量式稀疏重建思想,采用运动法(SFM)[18-19]求解不同视角下相机的外参数。SFM算法通过对多视角图像序列进行图像特征点的提取与匹配,建立图像特征点与三维重建点对应的映射关系,进而恢复相机外参数并优化。

如图3所示,I1与I2为相机在P1、P2两个位置的拍摄图像,对于欧氏空间中任意一个空间点X在I1与I2上的投影点分别为x1、x2。相机由P1位置运动到P2位置的相对旋转、平移变换分别记为RC、tC,则由对极几何约束可知

(2)

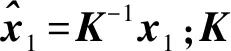
E=[tC]xRC

(3)

其中[tC]x为平移向量tC的反对称矩阵。应用SVD将E分解为如式(3)的形式,获得的tC与真实平移向量之间存在不确定的尺度因子λ。因此,图像信息只能准确计算相机在两个拍摄位置间的相对旋转矩阵。

相机拍摄I1、I2图像时,空间点X在相应两个相机坐标系下的坐标分别记为XC1和XC2,则满足

XC2=RCXC1+λtC

(4)

图3 相机外参数估计原理图

4 点云初始刚性配准

三维测量系统中每一视角下的局部坐标系、相机坐标系以及各测量站点的相机相对位置将点云数据间的位置建立了联系。基于图像信息的点云初始配准算法其实质是确定上述三者之间的变换关系。将局部坐标系下的点云转换到相机坐标系,根据序列图像重建过程中相机外参数估计结果,实现相机坐标系下点云的初始配准。

空间任意点X由三维测量装置得到的两个相应点云的坐标分别为XW1、XW2,则由式(1)可得

(5)

联立式(4)(5),三维测量装置在两测量站点间的刚性变换,即待配准点云间的刚性变换,可表示为

XW2=RXW1+t

(6)

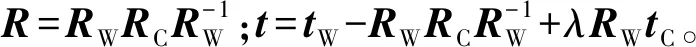
由于λ无法确定,故点云间的平移向量t并不能从图像信息中得到。因此,对式(6)简化得初始配准公式

(7)

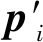
整个初始配准过程如下:通过扫描标定物标定相机坐标系相对于扫描仪坐标系(即点云局部坐标系)的位置变换RW、tW;应用SFM算法实现序列图像的相对定位RCi、tCi;通过RW、tW以及RCi、tCi计算点云初始配准的刚性变换参数,将变换参数作用于源点云对其刚性变换。初始配准流程如图4所示。

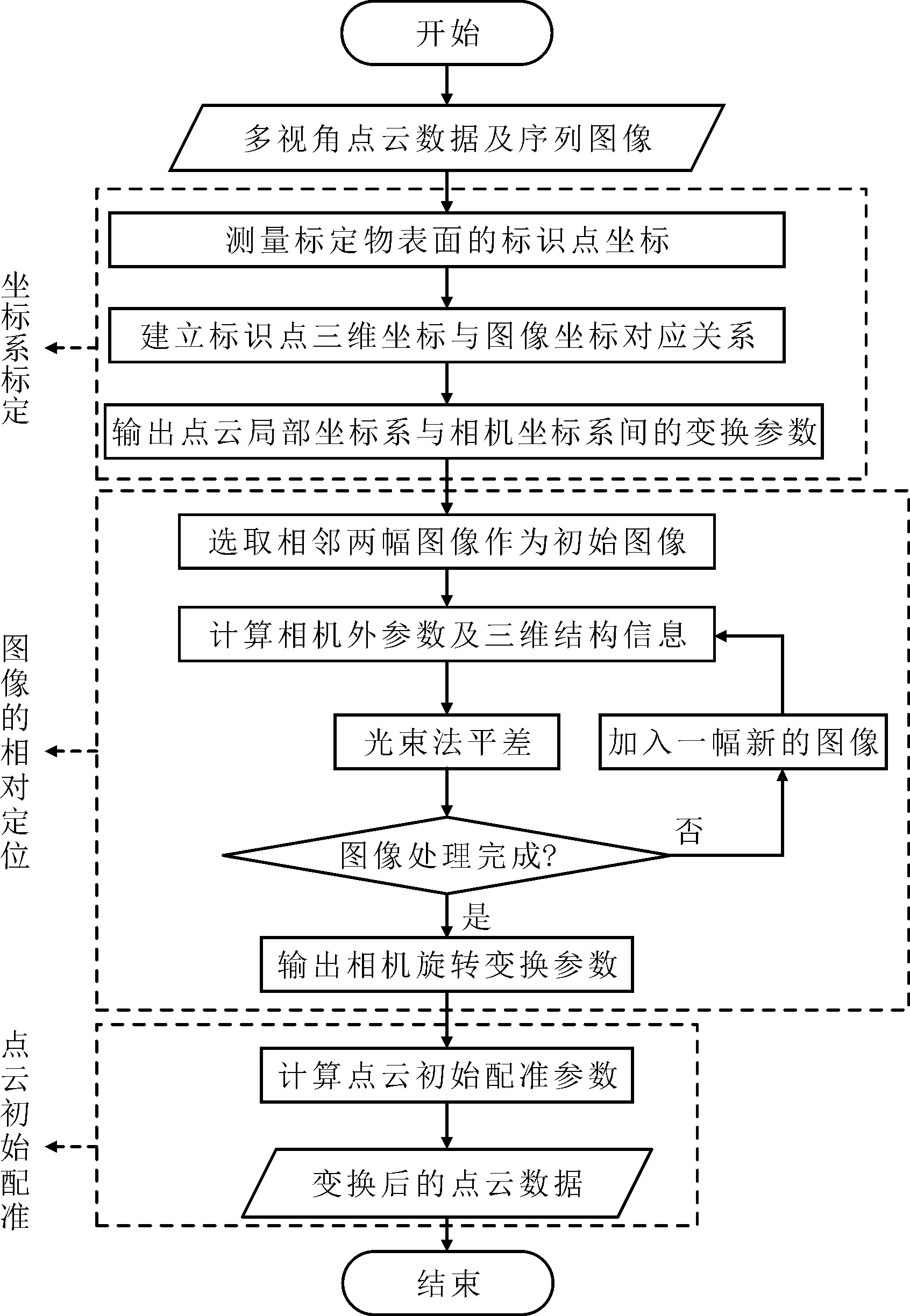
图4 初始配准流程

完成坐标系标定之后,计算点云初始配准参数具体步骤如下。

步骤1初始化相机运动信息和物体三维结构S(1)={XWl|l=1,2,…,n},其中,XWl表示重建得到的空间点坐标矩阵,n为空间点数,Ω={S(1)},Φ={M1,M2},k=2。

步骤2加入新的图像Ik+1,并提取SIFT特征点,对于Ik中的任一特征点在Ik+1中寻找欧氏距离最小和次小的两个特征点,若最小距离和次小距离之间的比值小于给定阈值α时,则认为最小距离对应的特征点是正确的匹配对,将特征点匹配对记为C(k)={Ik,k+1}。

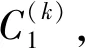
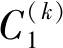
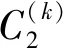
步骤6将S(k)添加到Ω。

步骤7采用光束法平差进行参数优化,并更新点集Ω以及相机外参数集合Φ。

步骤8k值增1。

步骤9重复执行步骤2～8,直至所有图像处理完成。

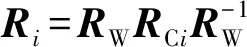
步骤11根据式(7)对点云进行Ri变换,将所得结果作为点云的初始配准结果。

5 实验验证与分析

实验中,移动光栅投影式三维扫描仪在位置A1,A2,…,An处采集被测物体的点云数据和图像,测量示意图如图5所示。为获得较好的视觉效果,实验中均显示的是精简后的点云数据。图6所示是5个视角下采集的Hood模型数据,图6a～图6e点数分别为150 423、156 506、191 188、191 238、177 400。图7为三维扫描仪在采集图6所示数据时拍摄的二维图像。

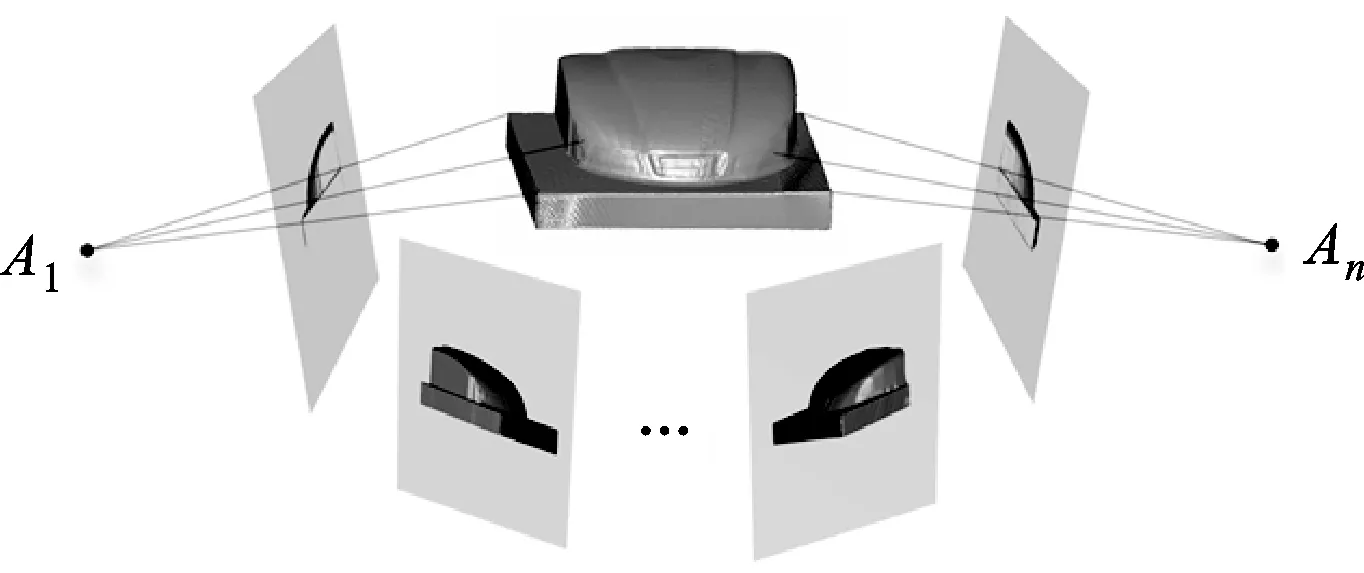
图5 模型数据测量示意图

为了测试初始配准算法的实际效果,以及验证ICP算法性能改善的结果,考虑到待配准点云是部分重叠的,故采用文献[20]中改进的ICP算法进行精确配准,在搜索最近点时,设定距离约束条件保留重叠区域内的点集以满足ICP算法对待配准点云之间存在包含关系的要求。在下文实验部分,称经初始配准算法优化后的ICP算法为SFM-ICP算法。在硬件为Inter(R) Xeon CPU 2.50GHz、内存为2GB、操作系统为Gentoo Linux、测试程序为C++的环境中测试。

(a)视角1

(b)视角2

(c)视角3

(d)视角4

(e)视角5

(a)视角1

(b)视角2

(c)视角3

(d)视角4

(e)视角5

(a)图像特征点初步匹配结果

(b)图像特征点去除误匹配结果图8 图7a与7b图像特征点匹配结果

SFM-ICP算法首先重建图7中5幅图像,计算出全部旋转变换矩阵。图8a、图8b展示了视角1、2对应的图像经SIFT特征点检测与匹配的实际效果,得到154对特征匹配点,实验中α取0.6,去除误匹配共获得23对匹配特征点;将视角1、2的旋转变换矩阵作用在待配准点云上,初始配准的结果如图9所示,两组点云之间仅相差一个平移变换。将当前的结果作为ICP算法的初始位置,进行精确配准,结果如图10所示。根据迭代得到的最近点对点云进行数据融合,并将其作为一组新的点云与下一视角的待配准点云,按照图8～10中视角1和视角2的配准过程完成配准。重复上述过程,直至所有点云配准完毕。表1所示为应用SFM-ICP算法对图6中不同视角下的Hood点云数据依次配准消耗的时间及均方误差。表1中第1组数据是指图6a与图6b中的点云,第2组数据是指第1组数据配准所得的新点云与图6c中的点云,第3组数据为第2组数据配准所得的新点云与图6d中的点云,第4组数据为第3组数据配准所得的新点云与图6e中的点云。Hood配准后的完整数字模型如图11所示。

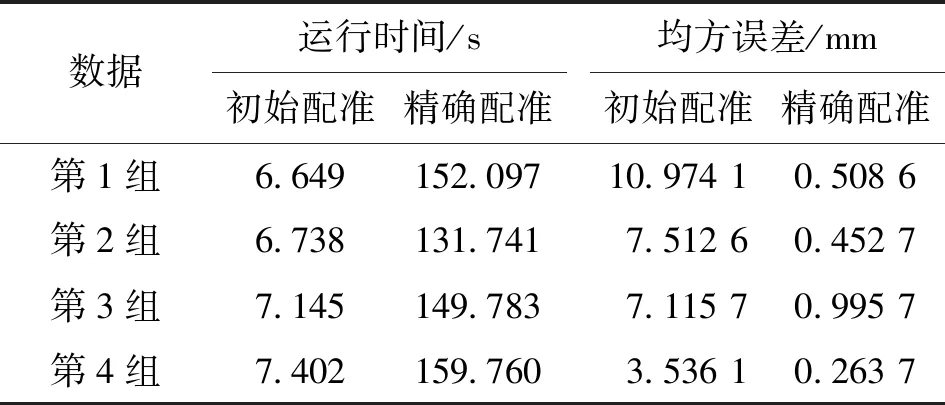
数据运行时间/s初始配准精确配准均方误差/mm初始配准精确配准第1组6.649152.09710.974 10.508 6第2组6.738131.7417.512 60.452 7第3组7.145149.7837.115 70.995 7第4组7.402159.7603.536 10.263 7

图11 Hood完整数字模型

为分析本文算法精度和稳定性,以人脸模型为对象,使用三维扫描仪围绕此模型在0°、40°、60°位置采集3组点云,3组点云的样点数分别为96 217、87 119、89 691;另外,在0°～60°移动轨迹内共拍摄7幅图像。将0°位置的点云分别与40°、60°位置的点云作为配准对象,以经典ICP算法[3]、MaxFS-based算法[11]为对比算法,对人脸模型不同视角的测量数据进行配准。

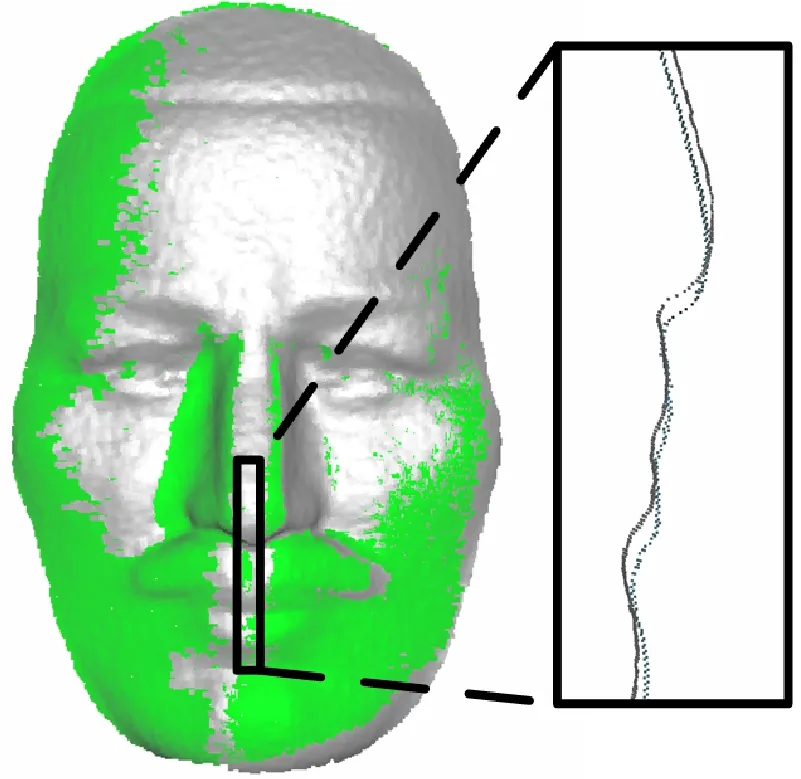
图12、图13分别为人脸模型的0°与40°、0°与60°位置的点云精确配准结果对比图,显示了点云局部位置截面图。此次实验,采用7幅图像对两视角点云的初始配准参数进行全局优化。由图12、图13可知:随着两点云初始位置之间旋转角度的增大,ICP算法配准错误,如图13b所示;MaxFS-based算法与SFM-ICP算法的配准误差仅是略微增大;本文的初始配准算法能够促进ICP算法收敛于全局最优解,提高算法配准精度。

(a)原始数据 (b)ICP

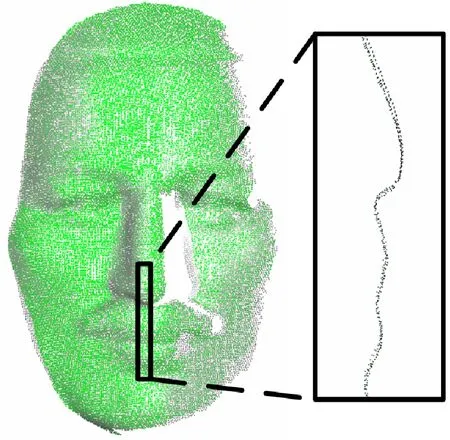
表2列出了图12、图13中3种算法配准结果在配准耗时以及配准误差上的对比。由表2可以看出:与ICP算法相比,SFM-ICP与MaxFS-based算法提高了配准的稳健性,对待配准点云初始位置的依赖性较小;SFM-ICP算法的实际时间复杂度最小,在计算效率以及配准精度方面取得了较好的平衡。

SFM-ICP算法根据二维图像的SIFT特征描述

(a)原始数据 (b)ICP

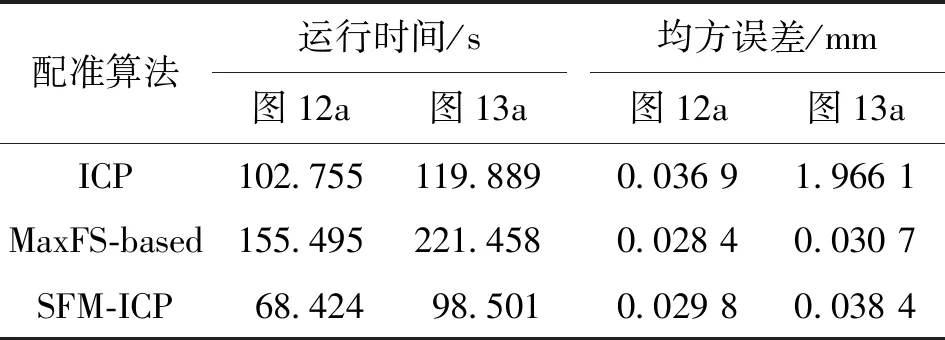
配准算法运行时间/s图12a图13a均方误差/mm图12a图13aICP102.755119.8890.036 91.966 1MaxFS-based155.495221.4580.028 40.030 7SFM-ICP68.42498.5010.029 80.038 4

子建立对应点,通过SFM算法全局优化旋转变换矩阵;MaxFS-based算法根据深度图像的方向直方图特征(SHOT)特征描述子建立对应点,并将配准问题转化为混合整数线性规划的分支定界问题,对旋转、平移变换参数进行全局优化。为对比两种算法达到收敛后的配准精度,以图12a的点云为实验对象,所计算的配准误差如图14所示,可见随着迭代次数的增加,3种算法能达到相同的配准精度。

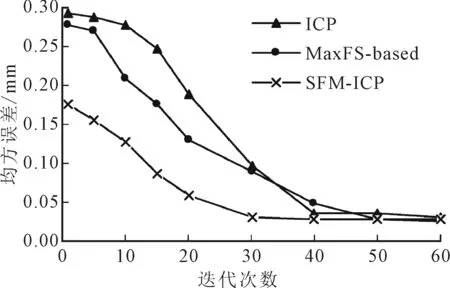
图14 3种算法的人脸模型配准误差比较

对图6中视角1和视角2下的点云数据进行不同程度的均匀精简获得5组新点集,然后保持前一实验所设的参数不变,分别应用3种算法对5组不同点数N的数据逐一配准,统计配准所用时间T,结果如图15所示。实验中,SFM-ICP算法通过重建图7中的5幅图像求解视角1、2的最优旋转矩阵。图16为SFM-ICP算法与ICP、MaxFS-based算法相比配准效率的提高率w,可见SFM-ICP算法可以显著提高配准效率,与ICP、MaxFS-based算法效率相比均提高了30%以上。

图15 3种算法的点云配准时间比较

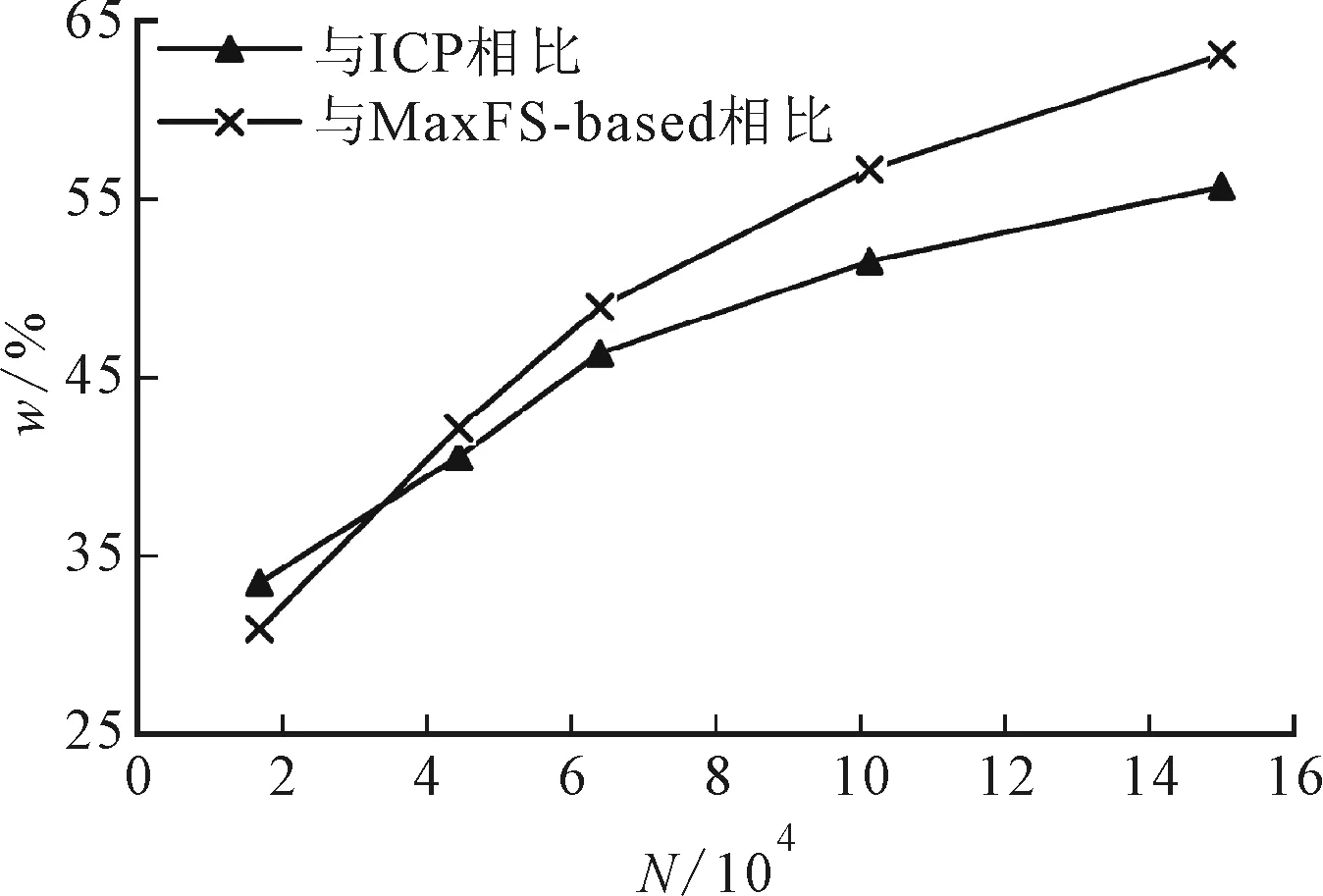
图16 SFM-ICP算法相比其他算法的配准效率提高率

6 结 论

本文基于透视投影原理实现相机在点云局部坐标系中的定位,并通过增量式重建序列图像对相机外参数予以全局优化,进而实现多视角点云初始配准。本文提出的实物表面采样数据的初始配准算法具有以下特点。

(1)可利用相机在不同视角下拍摄的图像间接获得点云间的旋转变换参数,且只需保证相机和光栅投影装置的相对位置固定不变,适用场合更广泛。

(2)基于序列图像特征点运动法重建的点云初始配准过程选取图像特征点作为控制点,根据其特征描述子匹配并筛选对应点,采用光束法平差进行全局优化,能精确求解待配准点云间的旋转变换。

(3)将点云配准问题转化为相机外参数估计问题,通过增量重建二维图像实现点云的初始配准,配准算法对点云初始位置无严格要求,稳健性得到提高。

(4)基于序列图像特征点运动法重建的点云初始配准算法确定的ICP算法初始参数,可明显提高ICP算法的迭代效率,配准效率提高约30%,并且随着点云数据规模的增大,配准效率呈递增趋势。