多项式回归模型系数变点的在线监测

齐培艳,段西发

(太原科技大学 应用科学学院,山西 太原 030024)

0 引言

宏观经济数据, 如商品零售额、居民消费价格指数(CPI)等, 通常会受到经济市场一些突发事件或政府决策的影响而发生变化, 即产生变点。因此,检测变点是否发生变化及何时发生对风险控制及方案决策等至关重要。同时,变点检测也是统计学的一个热点问题, 它把统计控制理论、估计、假设检验和样本抽样方法结合起来[1]。从抽样方法来分,变点检测分为连续抽样检测(即在线监测)和非连续抽样检测(离线检测)。对变点的离线检测发展较为成熟, 参见Sen和Srivastava(1975)[2], Csorgo和Horvah(1997)[3], Perron(2006)[4],Qian 和 Su(2016)[5]及Chen和Hu (2017)[6]等。Samaneh和Diane(2016)[7]指出非平稳数据的变点问题和变点的在线监测问题是变点分析领域未来的研究热点,对变点在线监测的研究主要集中在线性模型,Chu(1996)[8]首次考虑线性回归模型系数变点的监测问题;针对同一问题,Leisch(2000)[9]提出了广义波动监测统计量, Horvath等(2004)[10]基于最小二乘估计残差提出了两类残差累积和监测统计量,而Chen和Tian(2010)[11]在文献[10]的基础上,通过引进一个窗宽参数提出了一种改进的监测方法;Hsu(2007)[12]和Chochola(2008)[13]分别考虑线性回归模型和线性过程的方差变点的在线监测; Schmitz和Steinebach(2010)[14]讨论了多元线性回归模型的系数变点的监测问题。Qi、Tian 和 Duan(2015)[15]考虑位置模型方差变点的监测问题。近年, 对非线性模型变点的监测问题也有所发展, Berkes(2004)[16]讨论GARCH(p,q)过程参数变点的在线监测; Na and Lee(2010)[17]利用波动型监测统计量监测一阶随机系数的自回归模型的系数变点;Qi、Duan和Tian(2017)[18]采用滑动均方CUSUM统计量对非参数回归模型方差变点进行监测。多项式回归模型常用来拟合宏观经济数据,对此模型系数变点的离线检测问题已有研究[19-20],但对其系数变点的在线监测问题尚未见讨论。

本文讨论p阶多项式回归模型系数变点的监测问题。从构造一阶多项式回归模型系数变点的监测统计量出发推导出适用于p阶多项式回归模型系数变点监测的广义波动监测统计量。在无变点的原假设下, 给出监测统计量的渐近分布, 并模拟得到了部分临界值; 在备择假设下,证明其检验的一致性; 定义了停时过程。模拟结果表明本文方法是有效的。最后利用本文方法监测两组宏观经济数据的系数变点。

1 问题描述

假设观测数据Yt由以下模型生成

Yt=μt+εt,t=1,2,…,T,T+1,…，

(1)

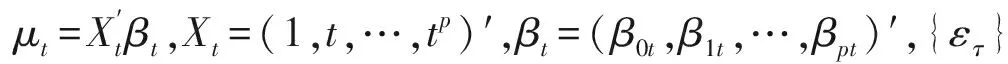
假设1误差序列{ετ}满足泛函中心极限定理,即∀s≥0有

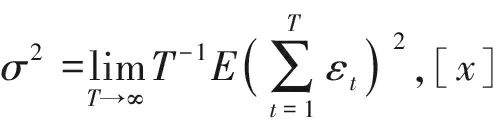
假定由模型(1)生成的序列y1,y2,…在指定时刻1,2,…被连续地观测到。假设已经观测到T个样本且这T个样本无污染, 即系数βt满足如下条件:

假设2βt=β0, 1≤t≤T.

本文在假设2的前提下,从第T+1个样本开始监测系数是否发生改变, 直到监测系统发出警报(出现变点), 或者到第N个样本结束监测(yT+1,…，yN为监测样本), 即连续检验如下假设检验问题:

H0:βt=β0,t=1,2,…,T,T+1,…，

HA:βt=β0,t=1,2,…,T,T+1,…,T+k*-1，

βt=βA,t=T+k*,…,N,β0≠βA，

其中参数β0,βA,变点k*≥1都是未知的。

注1这里设定最大监测样本量为N, 是考虑到实际应用中获取样本的成本因素, 当获取样本比较容易或成本较低时, 可令N=∞.

2 变点监测

本节从一阶多项式回归模型系数变点监测系统的构造出发,进而推导出适用于p阶多项式回归模型的变点监测系统,给出监测统计量原假设下的渐近分布并证明其在备择假设下的一致性。变点监测系统包含监测函数,边界函数和停时(系统发出警报的时刻)。

2.1 一阶多项式回归模型的变点监测

Kuan(1995,1998)[21,19]指出变点的离线检测中, 波动型检验统计量多以经验过程为基础构造, 故本文采取类似思想构造变点监测的波动型统计量。定义如下经验过程:

在无变点原假设下上式可化为

(2)

注意到(2)式中前两项是二次多项式,最后一项服从中心极限定理。若能通过某变换消除前两项,则变换后的经验过程在原假设下服从某一渐近分布。

考虑方程

Y(s)=b1s+b2s2+z(s)h(s)+z(s) ，

分别令s=1及s=u,u为大于1的一常数,则可得

由上述方程组可求得

即

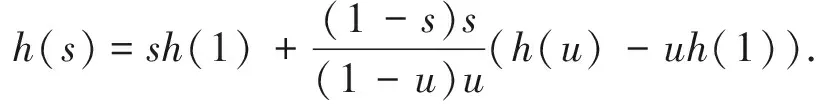
(3)

注2这里取s=1为了计算方便,b1,b2可由任意h(u),h(v) 表示, 其u,v>1,u≠v.

由(3)式可得

注意到上式中不含二次函数h(s), 故对经验过程做类似变换,

在原假设下可得:

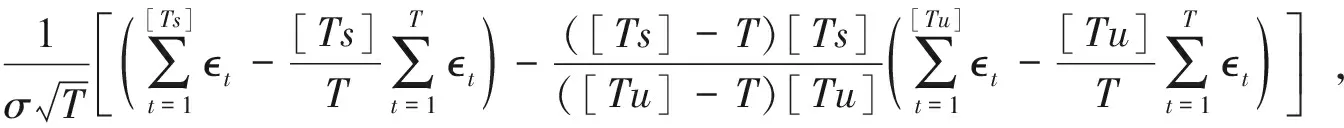
(4)

在备择假设下可得

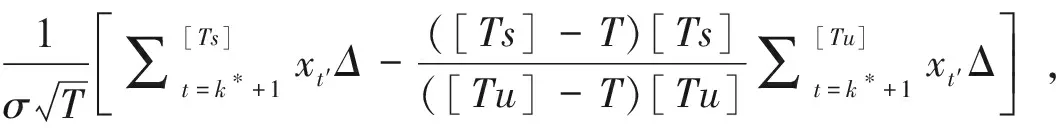
(5)

这里u为已知常数。由式(4)和(5)可知LT,uYT(s)在原假设下收敛于一维纳过程的泛函,在备择假设下可度量系数的变化量, 由此可定义如下监测函数:

(6)

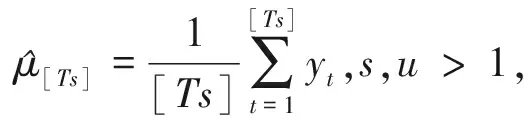
当新样本不断到来时,如果通过不停地对已抽到样本进行离线检测的方法来检验变点是否发生,则随着样本量的增大错报率趋于1,即在原假设成立时,以概率1拒绝原假设。因此需要设定一边界函数来控制错报率,本文边界函数定义为

g1(s)=([Ts]/T)2,1≤s<∞.

对不断到来的新样本计算监测统计量F1T(u,s), 如果存在s∈[1,q)(q=[N/T]), 使得F1T(u,s)>cg1(s),则拒绝原假设, 认为系数在某时刻发生了变化, 否则接受原假设。

由此可定义停时

τ=inf{T+1≤[Ts]≤N:F1T(u,s)>c([Ts]/T)2},

(7)

其中临界值c=c(α)可由以下两式确定

即在原假设下, 停时小于最大监测样本量的概率(错报率)不超过给定的显著水平α;而在备择假设下,当样本量趋于无穷时,以概率1拒绝原假设。

定理1 若假设1和假设2成立,则在原假设H0下有

其中W0(s)=W(s)-sW(1),W0(u)=W(u)-uW(1),s≥1,u>1,W(·)是一维纳过程,λ为定义在[1,q)上的连续函数。

证明

由假设1可得

则由连续映照定理可得定理结论成立。

注3常用的连续函数λ(·)有

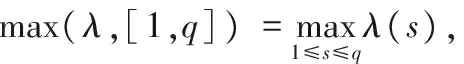
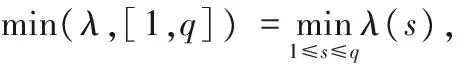
range(λ,[1,q])=max(λ,[1,q])-min(λ,[1,q]),

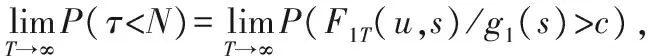
计算临界值c。

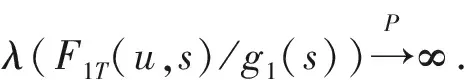
证明令Δ=βA-β0,∀ [Ts]>k*, 当[Tu]>k*时,

推论1 若假设1和假设2成立且βt=β0+Δ(t),t≥k*, 则在备择假设HA下

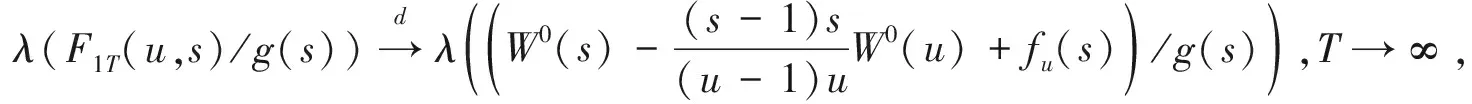
(8)

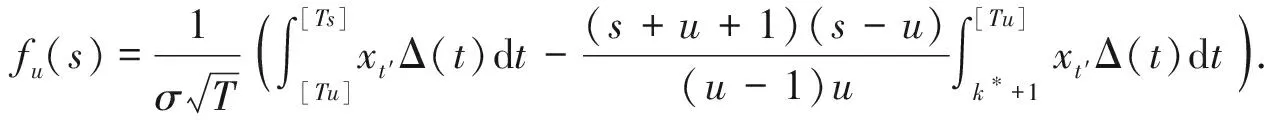
证明与定理2证明类似, 只需注意到

因此

从而可得(8)式。

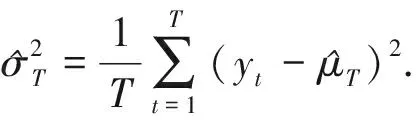
2.2 p(p≥2)阶多项式回归模型的变点监测

与上节类似,对于方程

hp(s)=b1s+b2s2+…+bpsp+bp+1sp+1,

存在一组常数ui>1,i=1,…,p,ui≠uj,i≠j使得b1,…,bp可由hp(1),hp(u1),…,hp(up)表示。

令U=(u1,…,up),则可定义如下监测统计量和边界函数

FpT(U,s)=LT,UYT(s),gp(s)=([Ts]/T)p+1,

则停时可定义为

τ=inf{T+1≤[Ts]≤N:FpT(u,s)>cgp(s)}.

类似地,关于监测统计量有如下定理和推论成立。

定理3 若假设1和2成立, 则在原假设H0下有

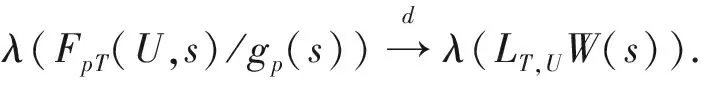
(9)

监测统计量的临界值可由下式计算

定理4 若假设1和假设2成立, 则在备择假设HA下有

推论2若假设1和假设2成立且βt=β0+Δ(t),t≥k*, 则在备择假设HA下

下面给出F2T(u,v,s),F3T(u,v,w,s)及fu,v(s),fu,v,w(s).

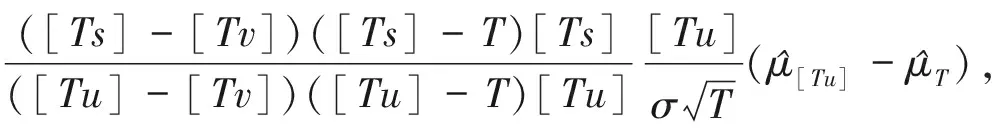
(10)

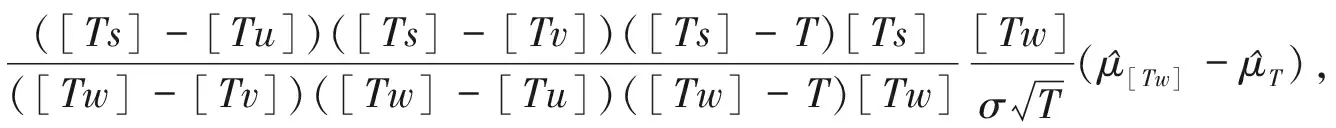
(11)

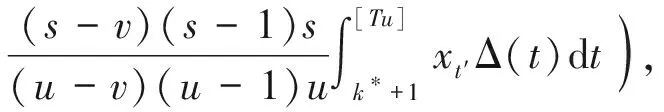
(12)

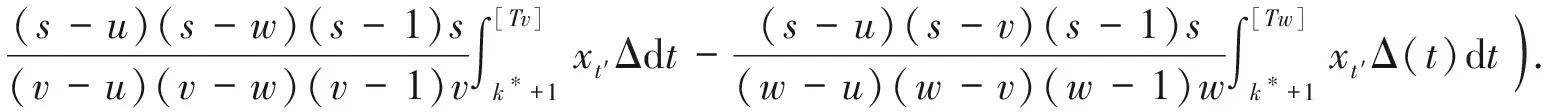
(13)

3 数值模拟及实例分析

3.1 数值模拟

表1 部分临界值

考虑数据由以下模型生成

yt=xt′βt+t,t=0.3t-1+et,et～IIDN(0,1).

考虑p=1 和p=2两种情形下系数变点的监测效果。在α=5%的显著水平下做模拟, 实验重复2 500次。当p=1时, 取历史样本量T=50,100,200, 最大监测样本量N=500,β0=[1,0.2];当p=2时,T=50,100,N=200,β0=[1,0.2,0.003].

表2为无变点原假设下的各监测统计量的经验水平。从表中看出,对线性时间趋势模型(p=1),当历史样本量较大时三种方法的经验水平都发生了扭曲,即都会发生错报。

表2 经验水平(%)

在备择假设下, 首先考虑变点发生时刻及历史样本量对监测效果的影响, 对不同的βA,表3-表4分别给出了p=1和p=2且λ(·)为max(·)时变点监测的检验势及平均延迟。由表可见, 变点发生的时刻对监测效果的影响很大。

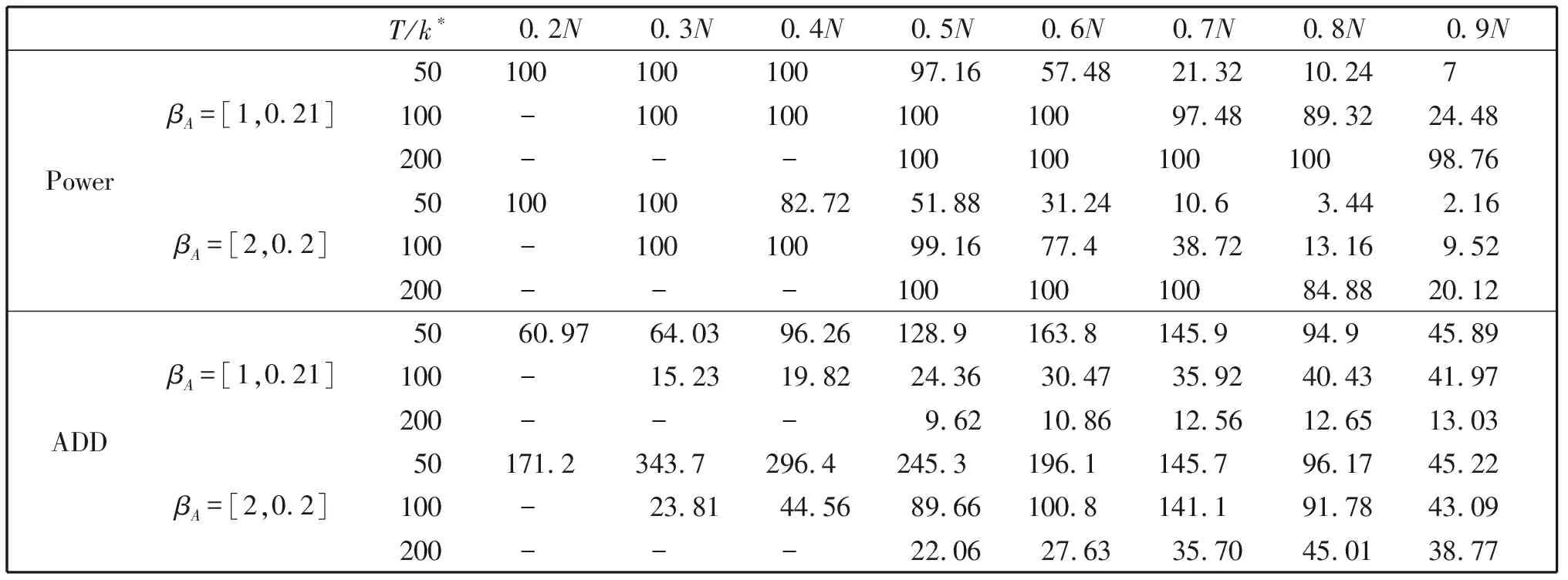
表3 max(F1T/g)的检验势(%)和平均延迟

对一阶多项式回归模型而言, 当变点发生较早时, 即使对较小的历史样本, 检验势也较高,几乎达到1;而当变点发生较晚时, 对解释参数变点和斜率参数变点的监测效果都不理想。 对p=2的情形, 随着变点时刻的推迟检验势明显降低而延迟明显增加,尤其是当历史样本量较小时。对同一变点, 检验势随着历史样本量的增大而增大, 平均延迟则随之缩短。

表4 max(F2T/g)的检验势(%)和平均延迟

下面分别在p=1和p=2两种情形下对本文所提方法max(·),Range(·)和CUSUM 方法的监测效果进行比较。表5给出了T=100时三种方法对一阶多项式回归模型系数变点的检验势和平均延迟。对解释参数变点, 当变点k*≤0.6N时,Range和max方法都能很好地监测到变点,而 CUSUM方法即使对发生较早的变点(k*=0.5N)监测效果也不理想,检验势较低,延迟较长;对斜率参数变点,Range和max方法对≤0.7N的变点监测效果都很好(检验势接近1,延迟很短),而当k*=0.7N时CUSUM 方法的检验势只有31.36%。

此外,从表中不难看出对两类变点,无论变点发生早晚,max方法略优于Range方法(个别情况除外),CUSUM方法的检验势明显低于另外两种方法,平均延迟又明显偏长;而随着变点发生时刻的推迟,三种方法的检验势都降低而平均延迟都增长,尤其是k*=0.9N时,平均延迟几乎达到最大(停时接近最大监测样本量)。三种方法对二次多项式回归模型系数变点监测的检验势和平均延迟见表6,与表5类似,变点发生越晚监测效果越差。对所有变点max方法的监测效果略优于Range,而CUSUM方法监测效果最差。

总之, 对p阶多项式回归模型的系数中的任何参数的变化, 本文方法都可以监测到, 而CUSUM方法对p≥2的多项式回归模型的系数变点几乎监测不到,即使p=1时本文方法也明显优于CUSUM方法。当历史样本量较小时, 本文方法对发生较早的变点监测效果很好, 而发生较晚的变点的监测效果较差。增加历史样本量可以改善监测效果,即提高检验势缩短平均延迟。 此外, 当系数变化较大或几个参数同时发生变化时, 监测效果更好; 对p≥3的多项式回归模型进行变点监测, 可得类似结论,在此不再赘述。

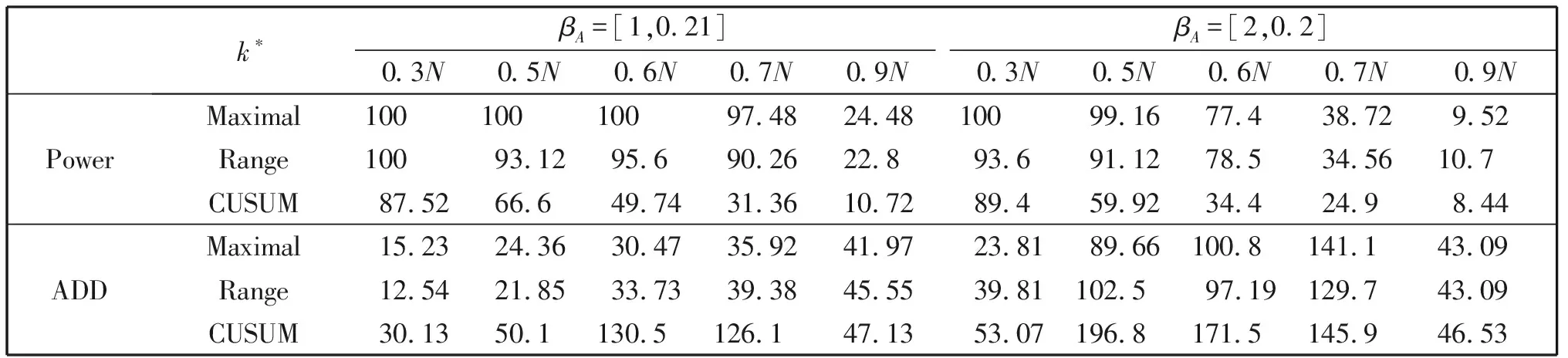
表5 λ(F1T/g)与CUSUM的检验势(%)和平均延迟

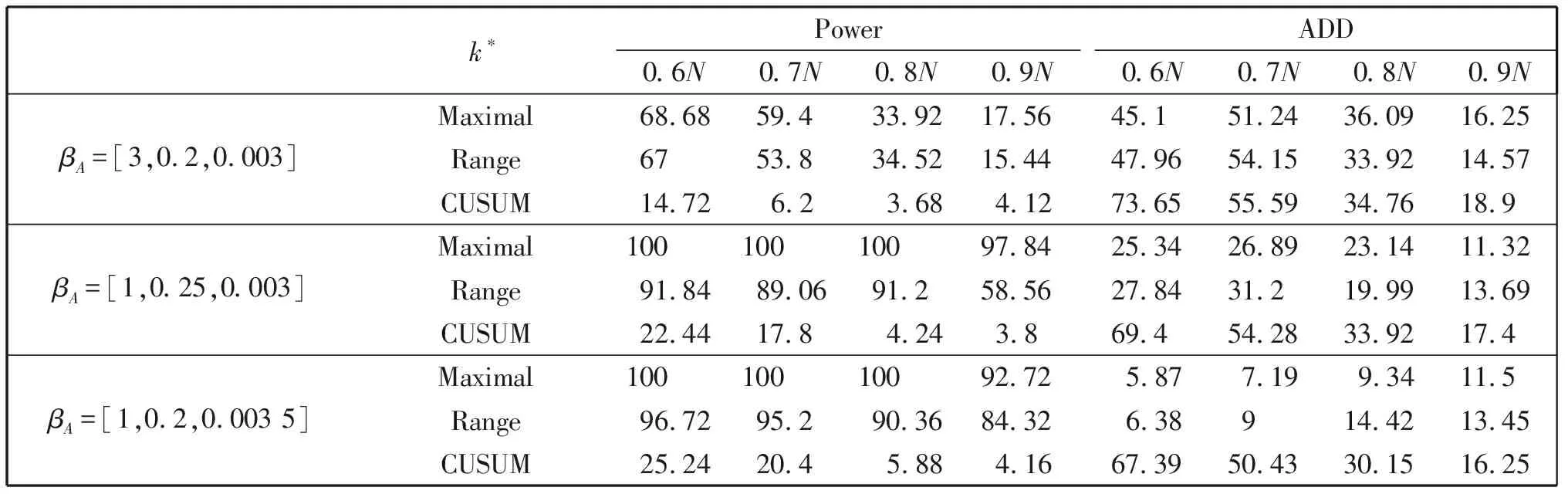
表6 λ(F2T/g)与CUSUM的检验势(%)和平均延迟

3.2 实例分析

本节利用本文方法对两组实际数据的变点进行监测,进而说明本文方法的有效性。

例1 考虑1952年到1983年我国社会商品零售总额, 共32个数据, 对数据进行二阶差分, 差分后数据在区间上均匀波动, 即其二阶差分数据平稳, 故该组数据可由二次多项式趋势模型拟合。取前5个样本作为历史样本,利用统计量max(F2T/g)进行变点监测, 在α=0.05 的检验水平下, 监测过程在t=13 处停止, 说明该组数据在用二次多项式趋势模型拟合时,在第13个数据之前出现了变点。

第13个样本观测值对应于1971年, 而在1971年之前的1968年,我国的商品零售额由往年的逐年增加突然变为减少,数据的变化趋势发生了变化,故而产生变点。

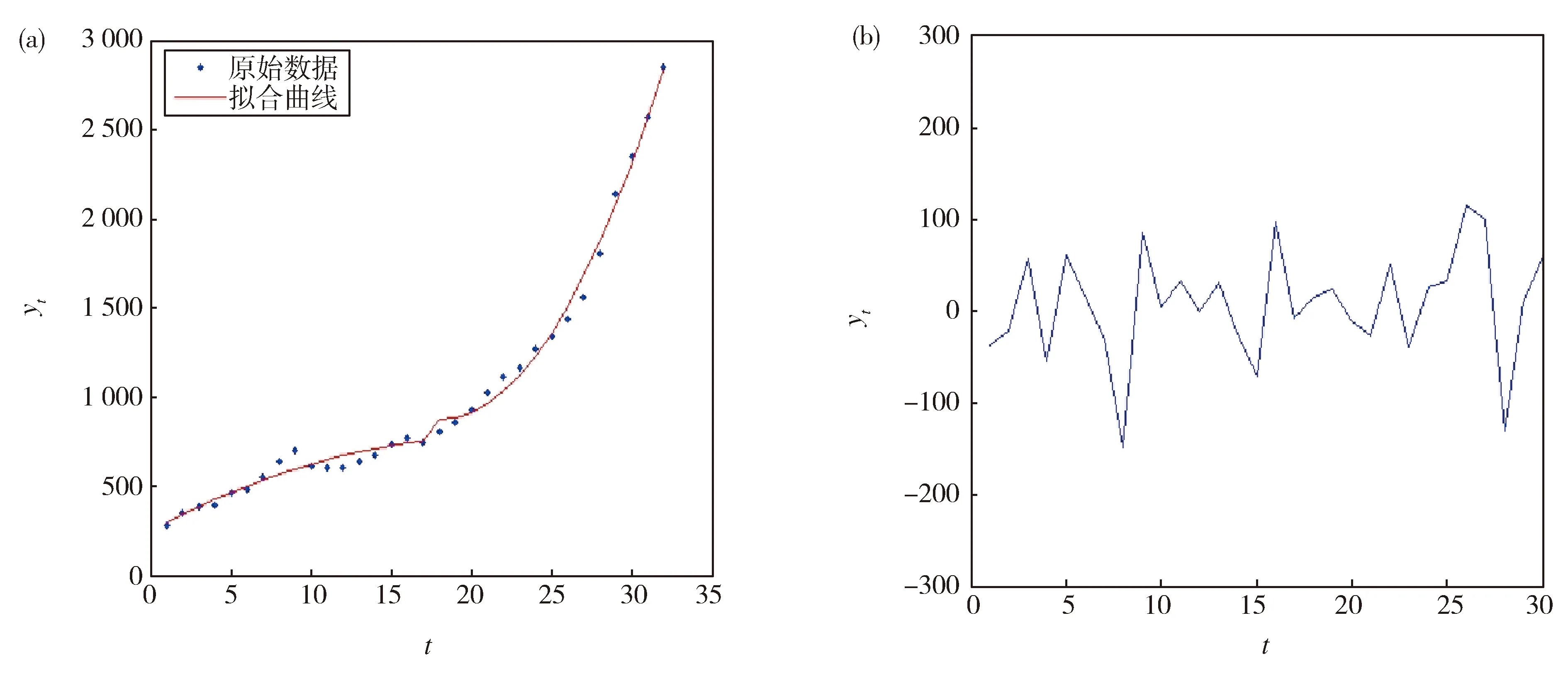
Fig.1 (a)Original data and quadratic polynomial fitting curve of total retail sales；(b)Second difference data图1 (a)社会商品零售总额原始数据和二次多项式拟合曲线；(b)二阶差分数据

例2 本例分析我国2008年1月到2012年3月居民消费价格指数, 共51个数据, 其二阶差分数据呈现平稳态势, 故该组数据可由二次多项式趋势模型拟合。取前10个样本作为历史样本,利用统计量max(F2T/g) 进行变点监测, 在α=0.05的检验水平下, 监测过程在t=26处停止,说明在第26个样本之前存在结构变点。

第26个样本观测值是2010年2月份的居民消费价格指数,在此之前, 受国际金融危机和国内经济增速下滑的影响,从2009年2月起我居民消费价格指数一直保持负增长状态,直到2009年12月才呈现明显的正增长态势。这可能因为我国持续扩大内需的政策有力地拉动了国内需求,一系列的补助政策的落实在一定程度上提升了居民的消费能力。

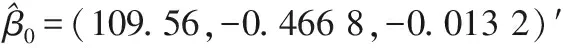
Fig.2 (a)Original data and quadratic polynomial fitting curve of consumer price index；(b)Second difference data图2 (a)居民价格消费指数原始数据和二次多项式拟合曲线；(b)二阶差分数据

4 结论

本文讨论了p阶多项式回归模型的系数变点监测问题。构造了监测函数和边界函数, 定义了停时过程, 推导出监测统计量的渐近零分布, 证明了检验的一致性, 并模拟得到了部分临界值。模拟实验中, 考察了本文方法的有限样本性质, 并将本文方法和CUSUM方法相比较, 结果表明本文方法是有效的而且具有更高的检验势和更短的延迟。最后将本文方法用于两组宏观经济数据的变点监测中, 得到了和文献[19]离线检测一致的结论, 证明本文方法可以很好地监测到变点。