曲射攻顶自寻的反坦克导弹制导控制规律研究*

王 磊

(北京特种机电研究所， 北京 100012)

0 引言

反坦克导弹在多山地区等复杂环境作战时易受其前方障碍物阻挡,为有效规避障碍物, 赵军民[1]研究了用于反坦克导弹飞行避障的弹道规划方法。王爽英[2]针对人因工程学在反坦克导弹武器操控系统的可行性应用,提出了人因学理论的实践、测试和评估方法。基于飞行器制导姿控原理，针对六自由度仿真需要的模型参数很难全部获取的问题，王宝和[3]建立了简化的三自由度弹道模型。吕鸿鹏[4]提出了一种虚拟试验方法,对基于引战配合的弹目交会毁伤概率进行了研究,针对某型反坦克导弹和某典型坦克进行仿真,验证了方法的有效性和正确性。李宏宇[5]等通过改变导航系数和调节滞后时间增大了制导炮弹的制导范围，提高了制导炮弹的制导自由度与初始状态的灵活度，提高了制导炮弹的制导精度。

自寻的反坦克导弹具备曲射攻顶能力后，可攻击坦克顶部薄弱部位，实现命中及毁伤，同时可大大提高战场适应性。

曲射攻顶自寻的反坦克导弹的射程为150 m至2 500 m，为保证在有效射程内始终具备曲射攻顶能力，需根据弹目距离自主实时控制弹道形式。文中在不使用惯导装置与激光测距机的前提下，利用导引头输出的弹目视线角速度和框架角、姿态陀螺仪输出的弹体俯仰角等信息，以及导弹速度和攻角设计值，建立了两种导弹自主估算弹目距离算法，实现了曲射攻顶自寻的反坦克导弹铅垂面内的弹道转弯点自主控制[6-7]。

1 基本假设

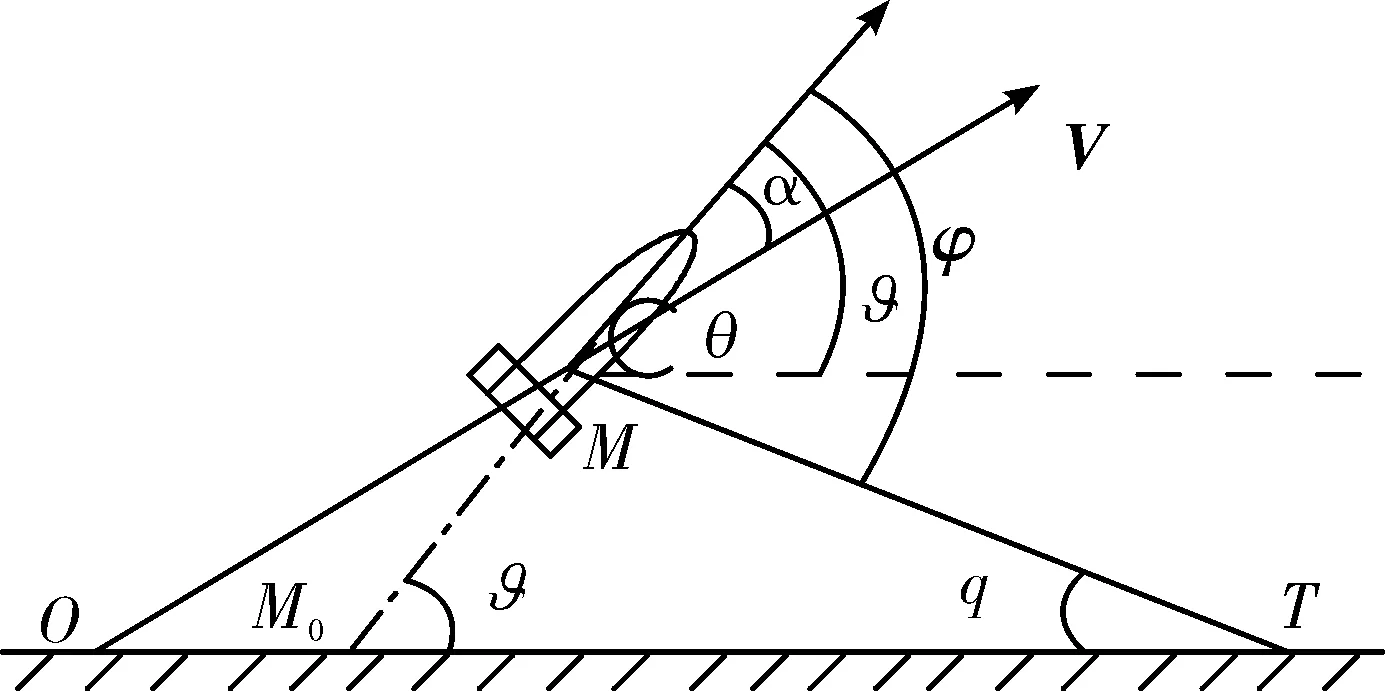
图1 ϑ、φ和q的相互关系图

在导引头锁定目标并稳定跟踪目标状态下，通过导引头框架角及弹体俯仰角能够计算得到弹目视线角q。ϑ、φ和q的相互关系见图1。其中，q=φ-ϑ，α为攻角，θ为弹道倾角。

2 弹目距离估计算法

2.1 弹目视线角估计法

为便于导弹自主估算弹目距离，将弹道上升段近似于直线，由此建立导弹与目标的相对位置关系，如图2所示。

图2 导弹与目标相对位置关系示意图

(1)

将式(1)变形可得各时刻的弹目距离：

(2)

为保证估算精度，选定导弹速度矢量变化平缓期作为估算弹目距离期。弹目视线角估计方法使用作为设计值的导弹速度信息，而这种控制方法虽然简单，但其控制精度却受到温度等因素影响。为研究干扰条件对弹目视线角估计法精度的影响，选定不同温度、风速、海拔高度作为典型干扰条件，仿真结果如图3～图5所示。

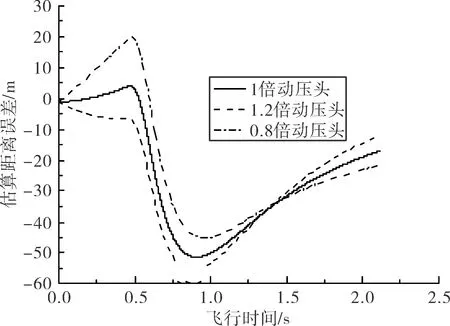
图3 不同温度条件下的估算误差

图4 不同海拔高度条件下的估算误差

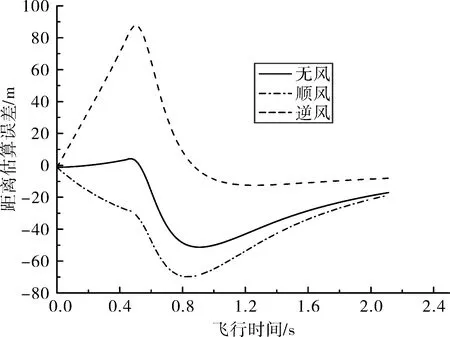
图5 不同纵风风速条件下的估算误差

a)温度

温度主要影响发动机的推力，温度不同时，发动机的推力不同。仿真结果如图3所示。

b)海拔高度

海拔高度将影响发动机推力、导弹速度和动压头，将3种干扰因素等效为动压头变化，仿真结果如图4所示。

c)风速

风速将直接影响导弹飞行速度，因只研究铅垂面内的弹道，所以只仿真纵风对估算精度影响。仿真结果如图5所示。

由图3、图4可见：弹目视线角估计法在估算初期的抗干扰性较强，但随着飞行时间增大，其估算误差逐渐增大；由图5可见：当风速不同时，在估算初始时期，其估算误差随着飞行时间增大，误差增大，但到达一个峰值后，估算误差逐渐减小。

2.2 弹目视线角变化率估计法

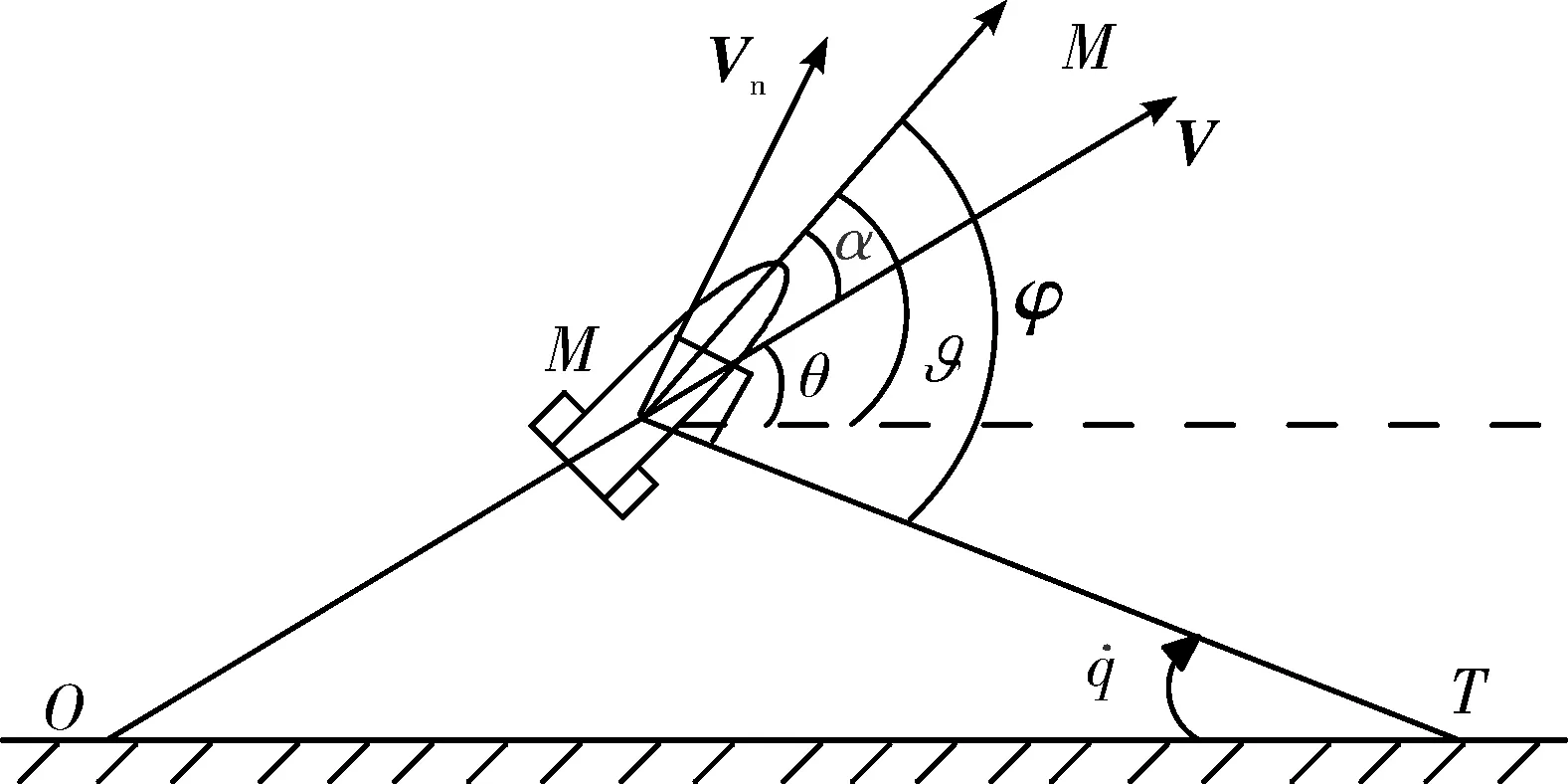
图6 弹目飞行示意图

为研究干扰条件对弹目视线角变化率估计法精度的影响，在与弹目视线角估计法相同的干扰条件下，仿真结果如图7～图9所示。

由图7可见，弹目视线角变化率法在估算初期对温度的抗干扰性较强，随着飞行时间增大，其估算误差呈逐步增大趋势；由图8和图9可见，在估算初期，海拔高和风速对弹目视线角变化率估计法影响较大，随着飞行时间增大，估算误差快速减小。

图7 不同温度条件下的估算误差

图8 不同海拔高度条件下的估算误差

图9 不同纵风风速条件下的估算误差

由数学仿真可见，在相同的干扰条件下，弹目视线角估计法的估算误差变化相对平缓，无发散趋势，且比弹目视线角变化率估计法要小，因此选择弹目视线角估计法估算弹目距离。

3 弹道制导控制规律

为保证导弹实现曲射攻顶，当目标初始距离不同时，图像自寻的反坦克导弹的弹道形式也不同，即铅垂面内的弹道转弯点不同。当目标初始距离较小时，导弹弹道只包含上升段和比例导引段；当目标初始距离较大时，导弹弹道包含上升段、巡飞段和比例导引段[10]。据此设计思想，图像自寻的反坦克导弹弹道控制规律如下：

1)上升段。采用固定弹道倾角爬升，其过载控制指令为：

ayc=kpitch(θc-(ϑ-αz))+gcos(ϑ-αz)

式中：ayc为过载指令，kpictch为与导弹过载能力相关的增益，θc为指定弹道倾角，ϑ为姿态陀螺仪输出值，αz为攻角设计值，gcos(ϑ-αz)为重补指令。

2)平飞段。采用固定弹道倾角飞行，其过载控制指令为：ayc=kθ(θc-(ϑ-αz))+gcos(ϑ-αz)

式中：ayc为过载指令，kθ为与导弹过载能力相关的增益，θc为指定弹道倾角，ϑ为姿态陀螺仪输出值，αz为攻角设计值，gcos(ϑ-αz)为重补指令。

3)比例导引段。采用比例导引制导律，其过载控制指令为：

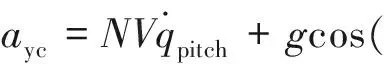
导弹实际工作过程是以剩余飞行时间对应的导弹飞行距离(Dmin)作为弹道转弯点的控制条件。由于导弹上升段按照固定弹道倾角爬升，且飞行速度已知，因此， 导弹转成比例导引的条件是剩余飞行距离(Dmin)大于等于弹目距离:

4 仿真验证

在给定弹体参数条件下，针对不同的目标初始距离(150 m、500 m、1 000 m、1 500 m、2 000 m和2 500 m)，利用弹目视线角估计法估算弹目距离，并按照设计的制导控制规律控制弹道，在以上条件下，对图像自寻的反坦克导弹弹道进行数学仿真，铅垂平面内的弹道仿真结果如图10所示。

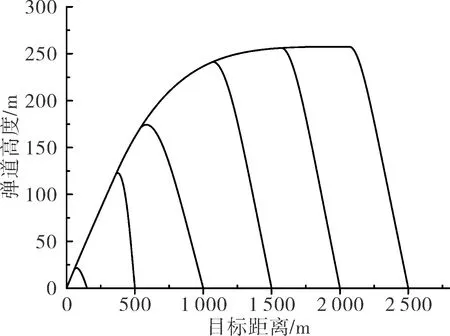
图10 不同射程条件下的弹道曲线

由图10可见，利用弹目视线角估计法估算弹目距离，并将该距离作为弹道控制条件，同时利用建立的制导控制规律控制弹道转弯点，实现了对不同距离目标的自主弹道控制。

5 结论

为降低导弹成本和射手操作负担，在不使用激光测距机等专用测距装置的条件下，提出了基于图像导引头和姿态陀螺测量结果的弹目距离估计的新算法，提出了一种导弹自主计算弹道转弯点的方法，建立了比较可靠的曲射攻顶的制导控制规律数学模型，为“轻型弹、大威力”的总体设计思想提供了理论依据。通过数学仿真验证了弹道控制规律的可行性。