库区滑坡涌浪传播及其与大坝相互作用机理研究
邓成进,党发宁,陈兴周
(1.西安理工大学 岩土工程研究所,陕西 西安 710048;2.中国电建集团 西北勘测设计研究院有限公司,陕西 西安 710065;3.西安科技大学,陕西 西安 710065)
1 研究背景
水库库区存在的滑坡、变形体、崩滑体等不良地质体,在不利因素影响下可能失稳高速滑入水库并产生巨大涌浪,危及大坝及下游安全,因此研究库区滑坡涌浪与大坝作用过程及其机理有着重要意义[1-2]。
库区滑坡滑动过程的滑速和涌浪计算受多种复杂因素影响,经验公式计算成为一种主要的、简便的手段,常用的经验公式有Noda E、潘家铮法、水科院法、美国土木工程学会法等[3]。任兴伟在潘家铮法的基础上提出了改进的经验公式,并用于计算新滩滑坡的初始涌浪高度[4]。水工物理模型试验也是分析库区滑坡涌浪及其作用机理的常用方法,比如李家峡库区1 号滑坡、龙羊峡库区近坝库岸、三峡库区龚家方崩滑体等工程均采用了大尺寸的水工物理模型试验研究滑坡涌浪对大坝安全的影响[5-7]。庞昌俊通过二维滑坡涌浪试验研究和探索了斜坡滑坡涌浪与水平、垂直滑坡涌浪的差异和关系[8];岳书波通过试验研究了滑块在水槽中形成涌浪的形态及衰减规律[9];这些试验总结了一些对滑坡涌浪问题的基本认识。大尺寸水工模型试验要获得完整的试验数据需付出较大的代价,尤其滑体高速滑动所带来涌浪剧烈变化而难以获取准确数据,限制了其推广使用。
由于流体力学Navier-Stokes 方程式求解复杂,当前一般从2 个方面来简化实现滑坡涌浪过程的数值模拟。(1)简化流体力学的方程模型。比如:钟登华等直接采用前述水科院经验公式,用三维可视化动态模拟技术分析了某水库滑坡失稳入库、激起涌浪的全过程[10];周桂云通过自编程序GEO-FLOW 将浅水控制方程应用于模拟滑坡涌浪的传播动态过程[11];黄波林采用基于水波动力学的FAST 软件,通过简化初始涌浪形成过程及涌浪源模型,对三峡库区茅草坡滑坡涌浪灾害、龚家方崩滑体滑坡涌浪进行了模拟和预测[12-13]。(2)采用简化的计算模型,即在二维剖面及小范围的三维水槽中来研究滑坡涌浪。缪吉伦等运用SPH 方法实现了模拟涌浪产生的过程[14-15];Viroulet 等采用二维SPH 法和有限体积法分别计算二维楔形滑坡涌浪规律,并采用水工物理模型试验验证[16];李静等采用SPH 法研究了小范围三维矩形规则水库中涌浪传播过程以及涌浪对大坝坝面的冲击力,分析了滑坡体宽度、入水速度以及库区水深对坝面冲击力的影响[17]。这些简化方法对于研究滑坡涌浪形成、传播过程及机理起到一定的促进作用;但无法考虑高坝大库的实际河谷地形,无法真实模拟滑坡涌浪形成及传播的全过程;尤其对于大范围的高坝库区数值模拟,模拟结果往往存在较大的误差。且很少有考虑下游大坝对库区滑坡涌浪传播的影响,以及滑坡涌浪与大坝相互作用的过程。
随着计算技术的发展,采用有限差分法进行水流、水力学模拟和分析在国内外得到广泛应用[18-19],但滑坡涌浪三维数值模拟的应用仍在探索阶段,其模拟的精度及可信度一直是关注的重点问题。本文建立了某高坝库区3#变形体的三维滑坡涌浪数值模型,并结合水工物理模型试验对其模拟的精度和有效性进行验证,为高坝库区滑坡涌浪数值模拟的应用提供科学依据;并通过数值模拟获得滑坡涌浪形成和传播过程的完整数据,分析和研究滑坡涌浪与大坝相互作用机理。
2 库区滑坡涌浪的水工物理模型试验
某高坝库区3#变形体位于大坝上游约1300 m(图1)。岸坡呈向河床凸出的弧形山梁,走向约NE30°,下游河流流向NE45°左右。岸坡范围为花岗岩体,沟梁相间,沟间为从岸顶到坡脚连续延伸的山梁,3#变形体即位于两沟之间,沟底一般有基岩出露。

图1 3#变形体与建筑物位置示意图
自水库蓄水后3#变形体倾倒变形大,变形条件及成因机制复杂,有必要分析极端情况下整体失稳下滑所产生的涌浪对大坝及下游安全的影响。为分析和研究滑坡涌浪对大坝安全的影响,建立了3#变形体库区滑坡涌浪的水工物理试验模型见图2。

图2 水工物理模型试验
试验过程参照《滑坡涌浪模拟技术规程》[20],模型满足几何相似、水流运动相似和动力相似,遵循佛劳德相似准则。滑体满足几何相似和块体的比重相似,河道和岸坡应满足阻力相似,几何比尺为λL=280,相应流量比尺为压力比尺为λp=λL=280,时间比尺为库区上游有足够的长度,以避免上游反射波较快折回与原生波向下游传递时产生叠加。
由于边坡表部岩体破碎,为方便观测滑体落入水中后的堆积形状,滑块根据试验方量由若干个标准块体堆积组成。滑坡体置于自制滑车上,滑车制成多节铰式,置于滑床上面,滑坡体可随滑车附贴着滑床下滑并取得较高的滑速;试验时由起吊、擒纵装置控制起吊及下放滑车,放置不同高度下滑可获得相应的入水速度。涌浪高度采用中国水科院水力学所研制的DJ800 型水工数据采集系统收集。水工模型试验开展了3#变形体在不同方量、不同滑速、不同水位条件的涌浪试验。试验在沿岸及大坝共布置了6 个涌浪测点(图1),1#—4#测点布置在左岸,基本代表涌浪沿岸传播规律及过程;4#—6#测点布置于坝前,代表涌浪与大坝相互作用过程。在正常蓄水位条件下,当滑体全部入水,滑速为24.6 m/s 时,各测点涌浪高度随时间变化曲线见图3所示。

图3 各测点浪高随时间变化曲线
由图3所示,各测点涌浪高度随时间不断动荡、起伏,在t=160 s 以后开始逐渐衰减趋于平缓。1#测点离落水点最近,其首浪高度最大;由于大坝的阻碍作用,4#测点处首浪高度比2#和3#测点的大,表明首浪高度随着离落水点的距离先减小后增加。坝前4#、5#和6#测点处水面起伏过程基本一致,河床中部(5#测点)首浪高度比两岸坝肩处(4#和6#测点)略小。坝前首浪高度在t=40~60 s 之间将大于坝顶超高,发生漫坝;随后水面反复震荡,在t=150~160 s 之间再次漫坝,此时两岸坝肩处(4#和6#测点)形成的涌浪最高。
3 基于流体动力学的滑坡涌浪数值模拟
3.1 基本理论将水流运动视为不可压缩的黏性流体运动,基于流体动力学采用离散完整的Navier-Stokes 方程式,通过体积分数和面积分数来定义网格中的障碍物,从而矩形网格能够精确地模拟复杂的几何形状。控制方程在描述上与经典方程有所不同,控制方程中含有体积分数和面积分数参数[21]。
Flow3D 采用有限差分法进行数值离散,将模型离散成空间矩形网格,而非常规的四面体或六面体网格,速度和面积分数参数位于矩形网格边界面的中心点上。求解方法采用广义的极小残差算法,其计算收敛速度相对较快,计算精度高,该方法在计算流体力学中得到了广泛的应用。
计算采用VOF 法追踪自由水面[22],引入了流体体积函数αq的概念,用于定义单元内第q 相流体所占体积与单元体积的比值,空气体积函数αq=0,流体内部体积函数αq=1,自由液面的体积函数为αq=0.5,实现了对自由面的追踪。若0<αq<1,则表示该单元为交接面单元。
RNG k-ε湍流模型可以很好地模拟高应变率和流线弯曲程度较大的流动。滑体入库及库区内涌浪相互作用时会导致水面出现巨大的变形、破碎,适合采用RNG k-ε湍流模型计算模拟滑坡涌浪的产生及其传播、作用过程。
3.2 库区三维滑坡涌浪数值模型将3#变形体简化为矩形刚性滑体,模拟在极端情况下整体滑动入水。滑体整体模型顺河向宽220 m,厚度为26 m,落水点水面宽度约为530 m,库区滑坡涌浪三维模型见图4所示。三维模型上游、左右岸及下游大坝采用固壁边界条件。模拟计算时间步△t=1.0 s,总计算时间步为160 s。
滑体滑动和堆积形态受河谷地形、以及水阻力的作用影响,且相互作用机理较为复杂,目前滑坡运动过程和堆积形态的模拟研究尚未有成熟办法[23]。结合水工物理模型试验的滑块速度成果,在FLOW3D 中自定义滑体滑动速度与时间的关系,以控制滑体运动过程,模拟滑体冲击水面及初始涌浪形成过程。
初始涌浪形成及涌浪爬坡过程中,水面发生剧烈变化,翻卷形成巨大的浪花,网格划分的疏密程度对水面变化剧烈区域的计算精度影响较大,但网格划分过于精细会造成数值模拟成本巨大,可能导致计算无法收敛[24]。对于高坝大库滑坡涌浪的三维数值模拟计算,为了提高计算精度,大幅减少网格数量,在水体剧烈运动的区域采用相对精细的网格,与其他区域的各网格块进行搭接。计算模型沿高程及河道分为9 个网格块相链接,滑体附近的河段及中部(正常水位附近范围内)网格适当精细,间距为2.5 m,其他网格间距5.0 m,模型网格化后共有单元约3325 万个,有效单元约1108 万个。
3.3 滑坡涌浪的形成及传播过程分析通过对库区滑坡涌浪整个过程的分析,可将滑坡涌浪形成及传播过程分为三个阶段:①初始涌浪形成及向对岸传播阶段;②沿岸传播阶段;③涌浪与大坝相互作用阶段。初始涌浪形成过程落水点附近水面高程云图见图5所示,在t=21~57 s 各时刻库区水面高程等值线图见图6。

图4 库区滑坡涌浪计算三维模型
(1)初始涌浪形成及向对岸传播阶段。随着滑体滑入水库,滑体挤压水体形成初始涌浪,涌浪由落水点向四周水域传播。在t=5~7 s 时由于滑体高速冲击水面,附近的水体受挤压后水面翻卷,迅速形成巨大浪花,表现为跃冲形态,形成了初始浪高。随着初始涌浪形成,在水面形成了一个以落水点为中心的波峰圈向四周扩散、传播。
(2)沿岸传播阶段。涌浪传播至对岸后,在岸壁阻挡和涌浪推进的双重挤压作用下,左岸附近水域水面呈整体抬升,在岸坡上爬升至最高后水体回落,并与再次形成的波峰相互作用、震荡。在落水点附近水面形成一系列涌浪传播圈,库区水体也随着升起、降落,推动着涌浪继续向坝前传播。在t=33 s 时涌浪传播至坝前水域,坝前水面开始缓慢上升。
(3)涌浪与大坝相互作用阶段。涌浪传播至坝前水域后,由于大坝及库岸阻碍作用,坝前水域的水面继续抬升,并逐渐在两岸坝肩位置形成较高的水面,在t=44 s 时两岸坝肩处水面高程达到坝顶高程2460.00 m;在t=52 s 时左岸坝肩处水面最大高程为2464.10 m,涌浪高度达12.10 m,超过坝顶约4.10 m,水体将漫过坝顶。随后坝前水域水面反复震荡,水体与大坝相互作用、叠加将形成更高的涌浪。
3.4 与水工物理模型试验结果对比分析将各测点处涌浪高度变化与水工物理模型试验结果进行对比见图7。由图7可得出以下规律:①1#—6#测点水工物理模型试验和数值模拟的涌浪高度变化及起伏过程基本一致。其中1#—4#测点处水工物理模型试验和数值模拟的水面起伏变化过程吻合程度较高;而5#、6#测点误差较大,两者吻合程度略有降低,但两者波动相似性依然存在。②各测点水工物理模型试验的首浪高度比数值模拟结果的大,计算存在一定误差。③测点离落水点的距离越远,两种方法得出涌浪高度的差别越小;随着涌浪的传播及能量消耗,后期两种方法得出涌浪高度的差别也越小。
数值模拟采用VOF 法追踪自由水面,网格划分精细程度对模拟涌浪浪花翻滚的清晰度影响较大。当数值模拟网格精细程度越高,就越能清晰的模拟出涌浪浪花翻滚、溅飞的微观形态,其计算的涌浪高度就大,即越接近试验或真实的水面高度。高坝大库三维数值模拟的网格却很难到达一定的精细程度,难以精确模拟滑体高速冲击水面、初始涌浪形成及涌浪传播过程中浪花翻滚的微观形态,因此各测点处数值模拟的首浪高度均比水工物理模型试验的小。随着涌浪传播,涌浪能量损耗之后,后期涌浪浪花高度逐渐减小,此时数值模拟与水工物理模型试验的涌浪高度也基本一致。因此,基于完整的Navier-Stokes 方程,采用有限差分法可实现库区滑坡涌浪的全过程,基本满足精度要求;但初始涌浪形成过程的浪花形态及对岸涌浪爬升等微观形态的模拟尚需采用更精细网格,以及付出更高的计算代价。
数值模拟可直观展示滑坡涌浪传播及其与大坝相互作用的整个过程,且与水工物理模型试验的涌浪高度变化趋势基本一致,数值上有一定误差,可为库区滑坡涌浪灾害预测和研究提供依据。

图7 各监测点数值模拟和模型试验涌浪高度对比
4 坝前涌浪及其作用机理分析
4.1 坝前涌浪高度分析滑坡涌浪传播的整个过程表明,由于大坝及库岸的阻碍,坝前水面先呈整体缓慢抬升,首浪传播至坝前时左岸坝肩处形成的涌浪最高。由4#测点(左岸坝肩)获得的数据表明(图7(d)),在t=44 s 时首浪超过坝顶;随着坝前水体相互作用、震荡,在t=151 s 第5 次波峰时,将形成水面最高。大坝左岸坝肩处在t=38~58 s和t=143~158 s各时刻涌浪形态变化过程分别见图8和图9。
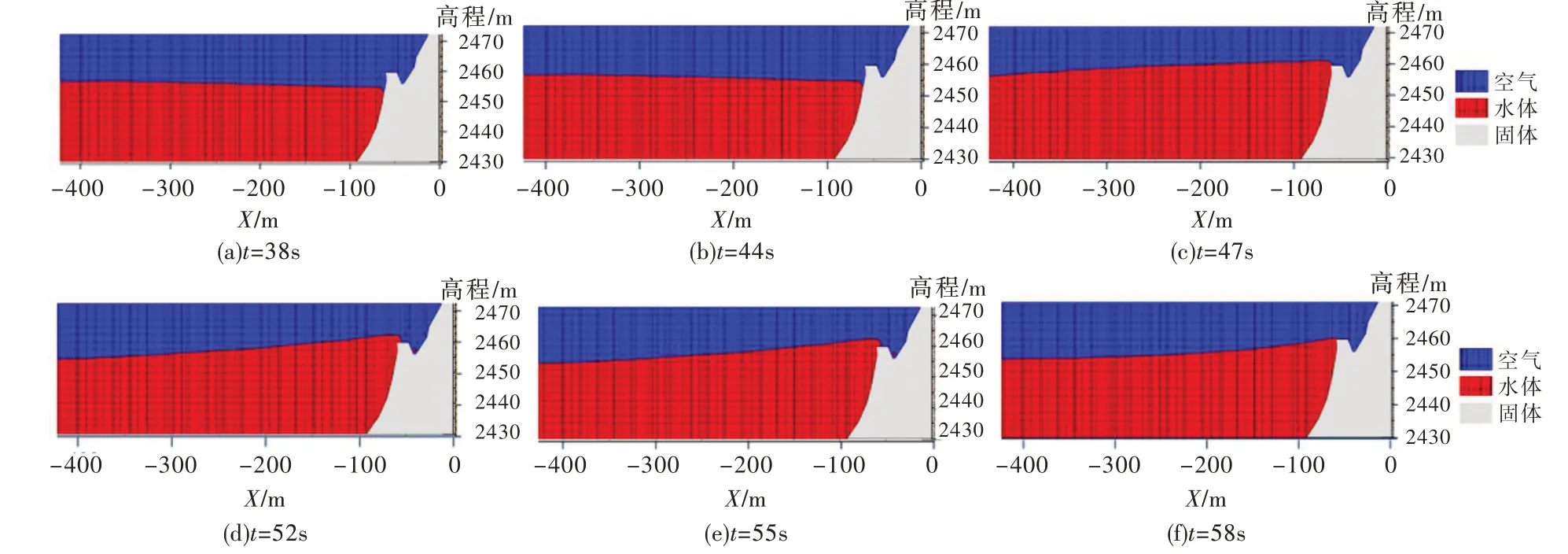
图8 在t=38~57s 各时刻左岸坝肩处水面高程
由图8可知,在t=44 s 时坝前涌浪达到坝顶高程2460.00 m,t=52 s 时达到最大2464.10 m,t=58 s时水面下降回落至坝顶高程,表明首浪可能在t=44~58 s 时左坝肩处缓慢的漫过大坝。
由图9可知,在第5 次波峰来临前,坝前水面形成了巨大落差,在t=148 s 时涌浪迅速冲上坝顶,形成巨大波峰,t=151 s 水面最大高程为2468.36 m,此时超过坝顶高程约8.36 m,比首浪更高。上述分析表明由于库区水面的反复震荡、叠加,坝前第5 次波峰形成的涌浪最高;与柘溪塘岩光(距大坝1550 m)滑坡涌浪的第2 次波峰达到最高的情况类似。

图9 在t=143~158s 各时刻左岸坝肩处剖面水面高程
滑坡涌浪传播至坝前,部分水体将在两岸坝肩处漫过坝顶,随后坝前水面下降,与后期传播至此的波峰相互碰撞,水面反复震荡、叠加将形成更高的涌浪。因此,有必要在坝顶及大坝下游建立避险空间,及时预警。
4.2 滑坡涌浪对坝体水压力作用分析随着滑坡涌浪与大坝相互作用,滑坡涌浪对坝体作用力也不断变化,因此分析坝面水压力变化规律对大坝稳定及应力有着十分重要的意义。大坝承受的水压力由静水压力P 和滑坡涌浪形成的动水压力ΔP 组成,涌浪产生的动水压力ΔP 与涌浪高度η 密切相关,故将各点的动水压力换算为动水头Δh=Δp γ,分析动水头Δh 与涌浪高度η 随时间的变化规律。通过数值模拟获得正常水位以下202 m 深处的坝面动水头及坝前涌浪高度随时间的变化规律,并与水工物理模型试验的监测数据进行对比(图10)。由图10可知,数值模拟和水工物理模型试验得出的动水头随涌浪高度的变化规律基本一致。动水头和涌浪高度的波动性基本一致,随着坝前涌浪高度增加,其动水头也逐渐增加,波峰时涌浪产生的动水头最大。在涌浪波峰、波谷处,动水头与涌浪高度的大小关系有所差别,表现为波峰时Δh <η,而波谷时Δh >η。

图10 动水头Δh 与涌浪高度η 随时间变化曲线
动水头不仅与涌浪高度相关,还与涌浪的波动频率、水深有关。定义波峰时动水头与涌浪高度之间的折减系数为由于模型试验的监测点有限,在数值模拟结果中获取在波峰时(t=45 s、85 s、158 s)折减系数沿大坝高程分布情况见图11。
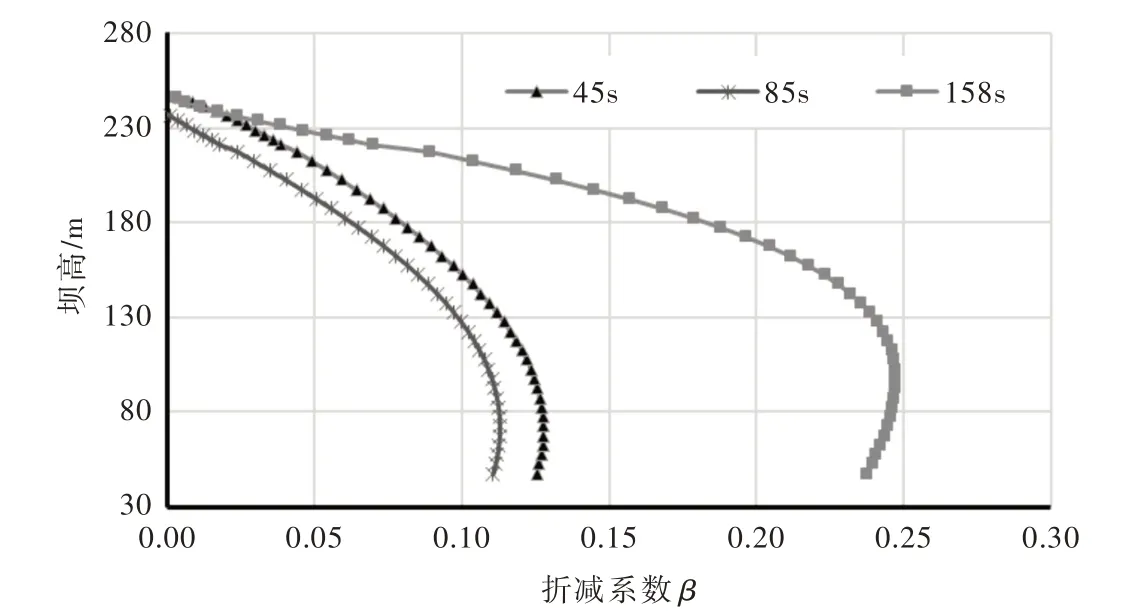
图11 数值模拟计算折减系数随坝高分布情况
由图11可得出以下结论:①在t=158 s 时动水头折减系数最大,而此时涌浪波动相对剧烈(图10(b)),表明涌浪波动频率越高,动水头与涌浪高度之间的相对差值越大,折减系数越大。②折减系数沿高程的分布规律基本一致,折减系数随着高程的降低先增后减,在0.3~0.4 倍坝高位置折减系数最大。③在t=158 s 时,由于涌浪波动频率较高,折减系数增大,其最大值出现的位置也相应抬高。上述分析表明,波峰时涌浪形成的动水头最大,动水头沿高程分布有一定程度折减,因此当直接采用涌浪水面的静水头作为大坝水压力计算时,结果偏于安全。
5 结论
本文以某高坝库区3#变形体整体滑动激起的涌浪为例,建立库区滑坡涌浪三维数值模型,并通过水工物理模型试验对数值模拟结果进行验证,研究了涌浪与大坝相互作用过程,得出以下结论:
(1)数值模拟得出的涌浪高度变化、水面起伏过程与水工物理模型试验的结果基本一致,但数值上有一定误差。随着后期涌浪传播及能量消耗,数值模拟与水工物理模型试验得出的涌浪与大坝相互作用过程及高度基本一致。数值模拟能较好地反映涌浪传播及其与大坝相互作用过程,可作为高坝大库库区滑坡涌浪灾害预测和预警的依据。
(2)滑坡涌浪传播至坝前在t=44~58 s 时两岸坝肩处漫过坝顶。在库区水面反复震荡、叠加作用下,在t=151 s 第5 次波峰时坝前涌浪最高,超过坝顶8.36 m,而后逐渐衰减。从涌浪灾害防治角度看,由于水体反复震荡、叠加而形成的涌浪可能会对下游沿岸和大坝安全造成更大危害。因此,有必要在坝顶及下游采取措施,建立预警系统和避险空间,在极端情况下及时预警、避险,直至涌浪衰减。
(3)高坝大库滑坡涌浪形成的动水头与涌浪高度、波动频率、水深有关。动水头与涌浪高度的波动性基本一致;波动频率越高,其与涌浪高度的差别也越大。波峰时涌浪形成的动水头最大,但动水头沿高程分布有一定程度的折减,折减系数随着高程的降低先增后减。因此当采用静力方法计算分析坝体稳定应力时,其计算结果偏于安全。

