NPTool模拟NaI(Tl)和LaBr3(Ce)闪烁体探测器试验研究

安少康

(核工业二〇三研究所，陕西 咸阳 712000)

Monte Carlo方法作为一种以概率论为指导的数值模拟方法，经过半个多世纪的发展，现在已经成为核物理研究方面的重要工具[1]。NPTool(Nuclear Physics Tool)是一款基于Geant4和Root开发而来的蒙特卡洛模拟和数据分析开源代码，主要用于核物理试验探测器的设计和低能核反应的计算机模拟[2]3。闪烁体探测器是一种辐射探测设备，利用核辐射与透明物质相互作用时，物质会被电离激发进而释放出光子的特性，对辐射进行探测。闪烁体探测器配合相应的光电倍增管和电子学仪器，在辐射探测方面具有灵敏体积大、探测效率高、价格低廉等特点。虽然闪烁体探测器的能量分辨率略差于半导体探测器，但由于其操作简单且环境适应能力强，仍然广泛应用于核物理试验中[3]231。

本试验模拟中，首先对开源的计算机模拟代码NPTool进行二次开发，编写并添加相应的函数库到代码中，使其满足闪烁体探测器的模拟要求；之后，对NaI(Tl)和LaBr3(Ce) 2种经典的闪烁体探测器进行模拟计算，得到这2种闪烁体探测器在不同试验条件下的γ能谱；最后，通过分析γ能谱得到这2种探测器在不同条件下的能量分辨率和探测效率，同时与Saint-Gobain公司的商业化闪烁体探头的测试数据以及前人的试验和模拟结果进行对比，进而说明NPTool可以用于闪烁体探测器的模拟分析。

1 NaI(Tl)与LaBr3(Ce)闪烁体

理想的闪烁体材料应该具有5个特性[4]：1)有能力高效地将粒子或光子的能量转化为可以探测的光；2)转化后的光强应当与粒子或者光子的能量成一定的线性关系；3)材料本身对于出射光应当是透明的，以保证较好的光子收集率；4)材料的荧光衰减时间足够短，从而可以产生较快的脉冲信号；5)材料的光学特性好，可以做成实际可用的探测器。随着材料科学的不断发展，到目前为止，已经被用来做闪烁体探测器并大规模应用于试验的无机闪烁体材料有NaI(Tl)、BGO(Bi4Ge3O12)、CsF、BaF2、CsI、GSO(Gd2SiO5)、LSO(Lu2SiO5)、YAP(Y1Si2O7)、PWO(PbWO4)、CeF3、LaBr3、LaCl3等若干种。这些晶体材料在闪烁体材料的5个特性上各有偏重，因此，可以根据不同的试验目的选用合适的闪烁体材料。

NaI(Tl)是最早被用于核探测试验的无机闪烁体材料之一，其晶体密度较大(3.67 g/cm3)，高原子序数成分多(碘含量85%)，透明系数好，光能产额、发光效率都较高，对射线探测效率也比较高，基本上满足了作为闪烁体探测器所需要的5个特性。在过去的射线探测试验中，NaI(Tl)曾作为表现最好的闪烁体探测器，被广泛应用于各种条件下的核探测试验中[3]242。LaBr3(Ce)则是近年来出现的一种新型无机闪烁体，与NaI(Tl)相比，LaBr3(Ce)闪烁体在大部分情况下表现更加优异，其晶体平均原子序数更高，晶体密度更大(5.29 g/cm3)，光能产额和发光效率更高，荧光衰减时间更短(十几纳秒)，时间和能量分辨率也更好，更适合进行射线探测[5]。所以，自从LaBr3(Ce)闪烁体探测器诞生以来，在涉及射线能量探测的试验中，各种性能更佳的LaBr3(Ce)闪烁体探测器开始逐步取代NaI(Tl)闪烁体探测器，成为了仅次于高纯锗探测器的选择。

本试验选择NaI(Tl)和LaBr3(Ce) 2种闪烁体作为研究对象，模拟2种闪烁体在不同的放射源条件下获取的能谱。通过分析能谱，与已知的试验数据进行对比，从而完成代码的编写和优化，使之可以用于闪烁体探测器的模拟试验。

2 建立基于NPTool代码模型

2.1 NPTool代码

NPTool代码的书写语言是C++，代码从结构上可以分为用户层、应用层和基础层3层，如图1所示[2]4。

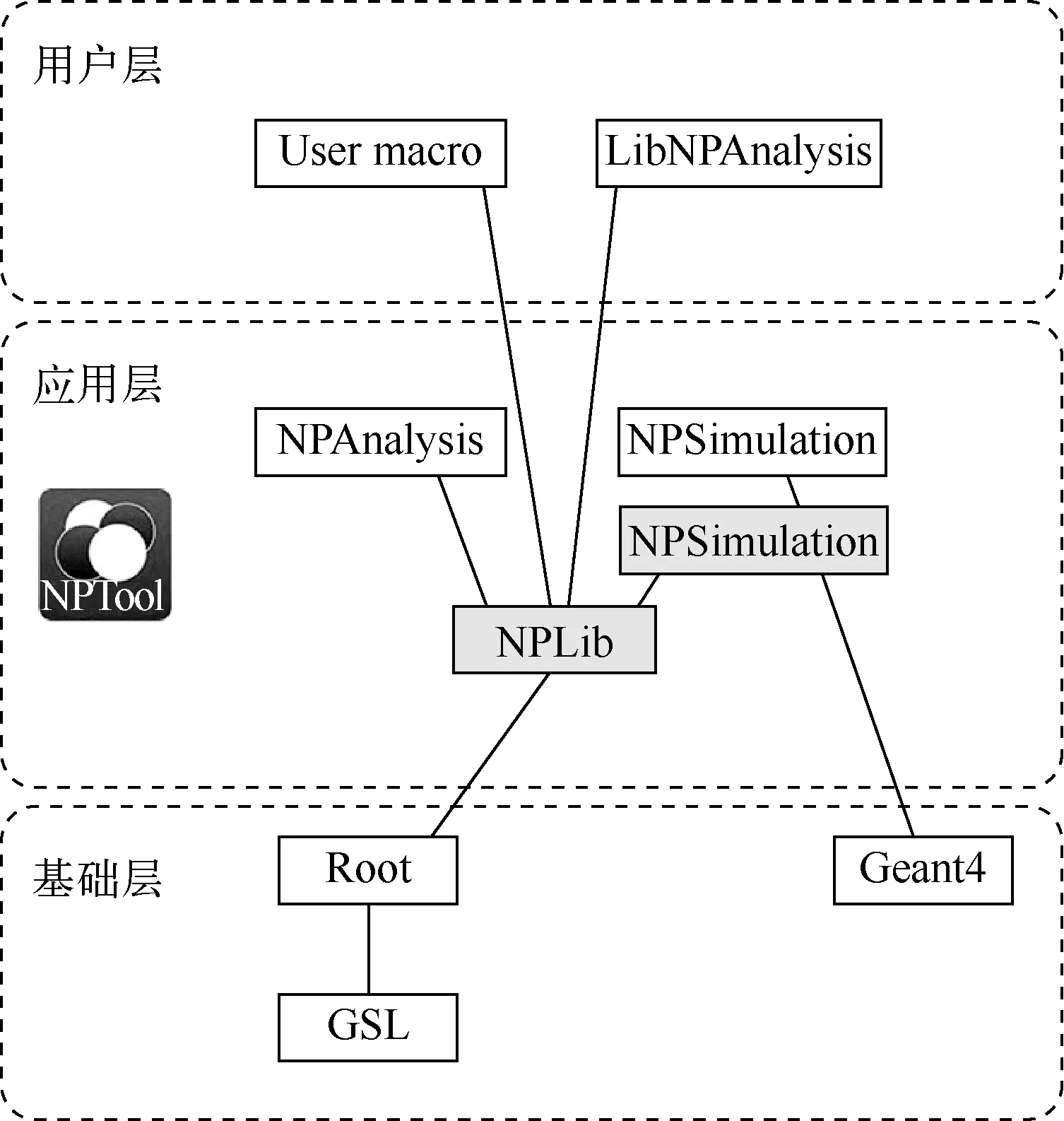
图1 NPTool代码结构示意

基础层主要包含代码进行Monte Carlo模拟所依赖的Geant4的库函数以及进行数据分析时需要的Root库函数。在使用代码时，用户首先需要安装Geant4和Root这2个代码，这样NPTool可以直接调用需要的函数库，一般不需要用户进行修改。应用层主要包含2个部分，分别为NPLib和NPSimulation。其中：NPLib用于模拟数据的输出、存储和分析；NPSimulation用于探测器的设计以及射线与物质相互作用物理过程的定义等。用户可以在这一部分根据试验需要修改或者添加相应的类，用于不同探测器和不同粒子相互作用的数值模拟，并对模拟过程中感兴趣的数据进行输出分析。本试验模拟中在该层添加相应的闪烁体探测器代码以及输出模拟得到的能量沉积信息。用户层则用于定义模拟中使用的粒子的种类、能量、状态，以及使用的探测器或探测器阵列的种类和空间位置；同时，用户也可以在这一层编写方便个人使用的数据分析代码用于试验数据的后处理。

2.2 探测器设置

本试验中，为NPTool模拟代码添加了名称为“NaI”和“LaBr3”的2个新的探测器，分别表示NaI(Tl)和LaBr3(Ce)这2种闪烁体探测器。这一部分需要在用户层和应用层完成，其中：用户层定义了探测器的尺寸空间结构，放射源的尺寸位置等情况；应用层则对探测器的材质、高能射线与物质作用时的作用截面以及能量损失等信息进行了定义。这2个探测器的参数设置如表1所示。

表1 NaI(Tl)和LaBr3(Ce)闪烁体探测器的参数

注：*这里假设光子产额与能量为简单的线性关系；而Geant4实际模拟时为非线性。

试验模拟的2种探测器均为7.62 cm×7.62 cm的圆柱形标准尺寸，密度分别为3.67 g/cm3和5.29 g/cm3。闪烁体探测器的使用会受到环境温度的影响，但是模拟中暂未考虑温度影响。由于闪烁体探测器的能量分辨率随着入射γ射线的能量近似于对数变化[6]，试验模拟在设计探测器时，使用方程(1)定义不同能量条件下闪烁体探测器的能量分辨率。

lnε=alnEγ+b

(1)

式中：a和b为方程的拟合参数；Eγ为入射γ射线的能量；ε为对应γ能谱全能峰的半高全宽(FWHM)。这种动态定义闪烁体探测器能量分辨率的方法会成倍增加计算机的计算量。通常情况下，在进行较差精度模拟时，可以将闪烁体探测器的能量分辨率定义为一个固定值。

2.3 放射源设置

模拟采用的放射源为点状的γ放射源。模拟代码通过设置不同的能量峰以及对应的强度来模拟不同的放射源，试验分别模拟了57Co(0.122 MeV，0.136 MeV)、137Cs(0.662 MeV)、60Co(1.173 MeV，1.332 MeV)、133Ba(0.081 MeV，0.303 MeV，0.356 MeV)以及208Tl(2.615 MeV)等5种放射源的多个不同强度的能量峰。放射源与闪烁体探测器之间的距离分别设为5 cm和2 cm，以获取不同条件下2种闪烁体探测器的探测效率和能量分辨率，方便与试验测试数据进行对比。将2种条件下2种探测器的探测效率与文献[7]81-83中的试验和模拟数据进行对比；将模拟得到探测器的能量分辨率及探测器探测效率的相对值，与Saint-Gobain公司商业化探测器使用手册中的测试数据进行对比[8]21。

模型建立完成后的效果如图2所示。其中灰色圆柱体为NaI(Tl)或者LaBr3(Ce)闪烁体探测器，白色圆盘的中心为放射源的位置，白色射线则为模拟放射源放出的γ射线。

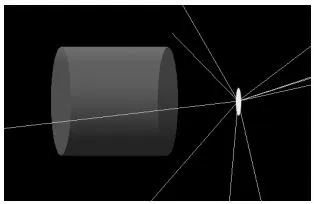
图2 试验模型示意

3 模拟结果及讨论

模拟试验中的γ放射源各向同性的释放出107个γ光子，以降低统计数目带来的误差。探测器位于距离γ放射源5 cm处，得到不同能量的γ光子在NaI(Tl)和LaBr3(Ce) 2种闪烁体探测器上的能量沉积谱。

3.1 不同放射源的能量沉积谱

为了方便对比，将同一种放射源在不同闪烁体探测器上的能量沉积谱绘制在同一张直方图上，如图3所示。

图3 137Cs能量沉积谱

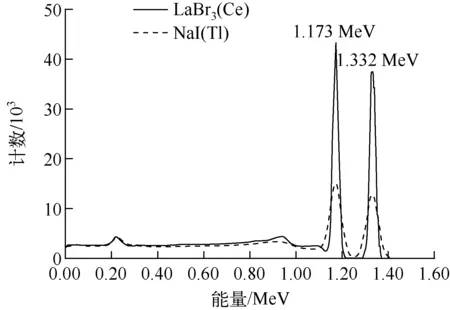
图4 60Co能量沉积谱

图3是NaI(Tl)和LaBr3(Ce)闪烁体探测器获取的的137Cs的γ能谱，其中虚线为模拟NaI(Tl)闪烁体探测器得到的能谱，实线为模拟LaBr3(Ce)闪烁体探测器得到的能谱。从图中可以看出，在0.662 MeV全能峰位置，LaBr3(Ce)闪烁体探测器的能量分辨率要好于NaI(Tl)闪烁体探测器。这是由于同等条件下，LaBr3(Ce)闪烁体的光子产额要高于NaI(Tl)闪烁体；另一方面，由于LaBr3(Ce)闪烁体原子序数较大，晶体的密度也大于NaI(Tl)闪烁体，所以整体的探测效率高于NaI(Tl)闪烁体探测器。同样，将60Co、208Tl、57Co、133Ba放射源的γ射线能量沉积谱依次在图4～7中进行对比。可以看出，无论是低能区还是高能区，LaBr3(Ce)闪烁体探测器的能量分辨率都要好于NaI(Tl)闪烁体探测器。由于闪烁体探测器的能量分辨率随着γ射线能量的降低而变差，在图6和图7中的低能区部分，LaBr3(Ce)闪烁体探测器仍然具有良好的能量分辨率；而NaI(Tl)闪烁体探测器已经无法将低能双峰结构区分开。模拟结果与文献[8]35-37中的试验测试结果整体符合。

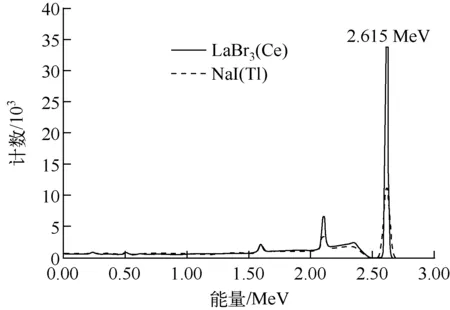
图5 208Tl能量沉积谱

图6 57Co能量沉积谱

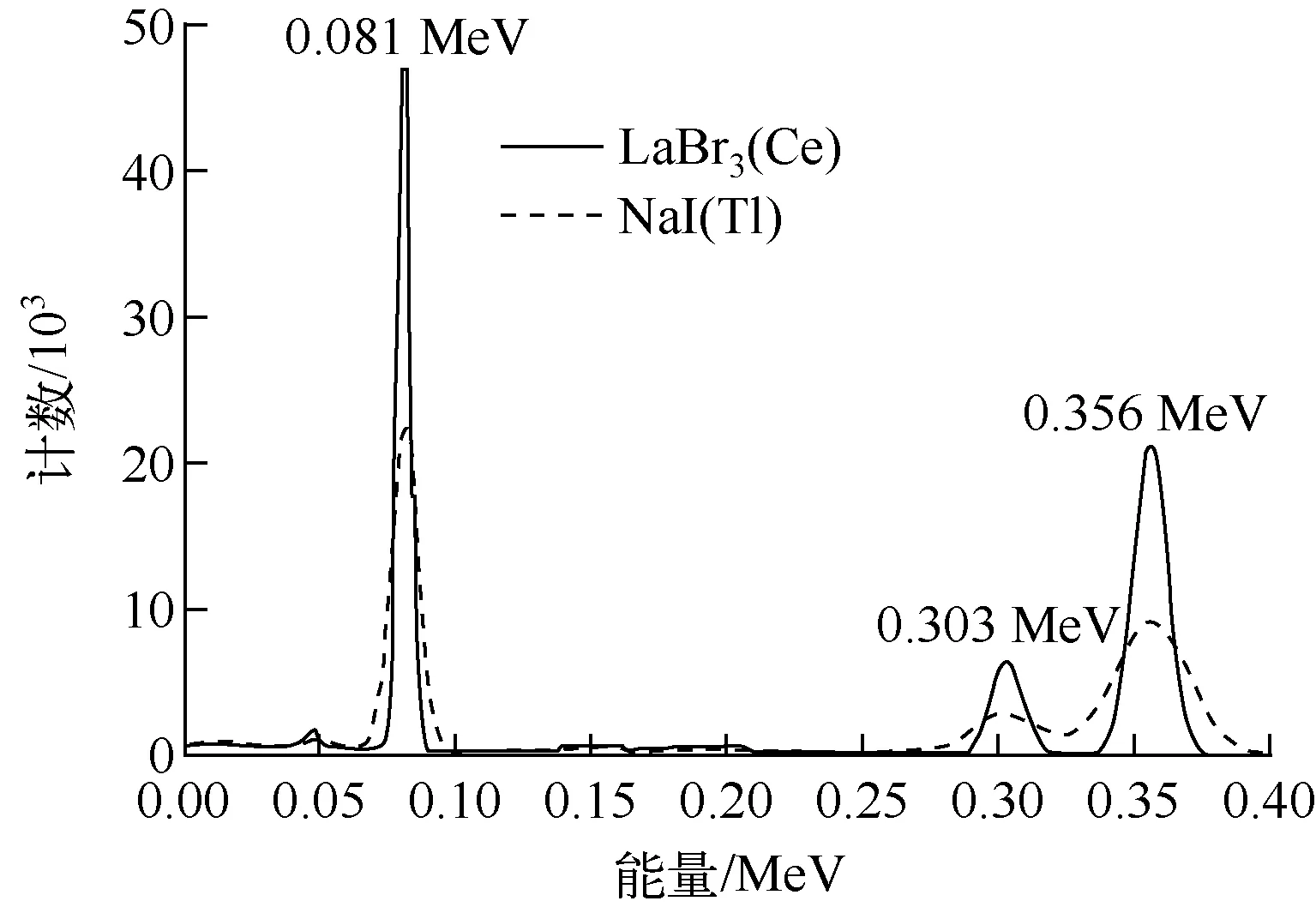
图7 133Ba能量沉积谱

3.2 能量分辨率对比

闪烁体探测器的能量分辨率主要由3个因素决定：1)闪烁体自身固有的分辨率。发光效率越高，光能产额越大，透明度越好，荧光衰减时间越短，则闪烁体的固有分辨率越好。显然，LaBr3(Ce)闪烁体探测器的固有分辨率要好于NaI(Tl)闪烁体探测器。2)配合使用的光电倍增管(PMT)的分辨率。光电倍增管与闪烁体的发光频率匹配的越好，打拿极电子倍增线性度越好，则分辨率越好。3)后续电子学数据获取设备的分辨率。本试验模拟中不涉及到光电倍增管和电子学设备，模拟结果得到的LaBr3(Ce)闪烁体探测器获取的γ射线能量沉积谱的能量分辨率远好于NaI(Tl)闪烁体探测器。在实际应用中，由于光电倍增管和后续电子学设备对2种闪烁体探测器能量分辨率影响的贡献基本一致，所以试验模拟得到的能量分辨率可以反映探测器在实际应用中的表现。

试验模拟中，以γ射线能量沉积谱全能峰的半高全宽(FWHM)与全能峰能量的比值ΔE/E作为衡量闪烁体探测器能量分辨率的依据。在进行数据分析时，首先利用Root数据分析代码，使用反卷积法在扣除必要本底的同时，精确获取全能峰的峰位值信息；之后利用峰位值信息，使用最小二乘法进行高斯拟合，获取全能峰高斯拟合的σ值；最后通过计算得到探测器的能量分辨率。以137Cs的0.662 MeV全能峰为例，试验模拟得到的高斯拟合图谱如图8所示。

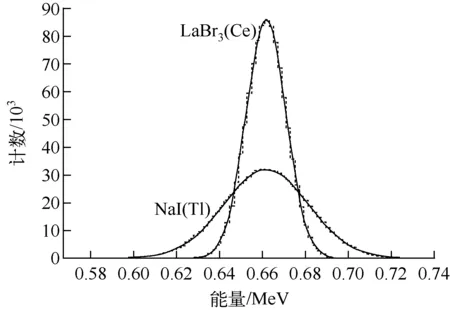
图8 137Cs全能峰高斯拟合结果

从图8拟合得到的LaBr3(Ce)闪烁体的能量分辨率为3.33%，NaI(Tl)闪烁体的能量分辨率为7.01%。使用该方法统计57Co(0.122MeV)，137Cs(0.662 MeV)，60Co(1.332 MeV)，133Ba(0.356 MeV)以及208Tl(2.615 MeV)等5种放射源的5个全能峰，得到相应的全能峰位置的能量分辨率，如表2所示。

表2 NaI(Tl)和LaBr3(Ce)闪烁体探测器的能量分辨率

通过对比发现：试验模拟中得到的2种探测器的能量分辨率与参考文献中的试验测试结果基本一致；但在57Co 0.122 MeV全能峰处，NaI(Tl)闪烁体与文献[8]45中的试验值相差较大。分析认为，自然本底在低能区较强，实际测试中进行峰信息拟合时的误差较大，文献[8]20-79中进行试验测试和数据分析时存在一定的问题，从而造成文献中这个数据点偏离统计趋势较多，理应舍去。因此，本试验模拟中的参量设置适当，模拟结果是真实可信的。

3.3 探测效率对比

本试验模拟参考文献[7]80中的做法，以全能峰的统计计数与放射源释放的γ光子总数的比值作为闪烁体探测器的探测效率，使用公式(2)计算。

(2)

式中：Deff表示探测器的探测效率；C为全能峰的计数；R为全能峰的强度；n则为总的γ光子数目，本试验模拟中n=107。在完成各个全能峰的高斯拟合之后，试验以137Cs(0.662 MeV)、60Co(1.173 MeV，1.332 MeV)和133Ba(0.081 MeV，0.303 MeV，0.356 MeV)为研究对象，统计全能峰5σ以内的统计计数C，除以该全能峰的强度R，再与试验模拟是放射源释放的γ光子的总数n=107做比值，得到的探测效率统计如表3所示。

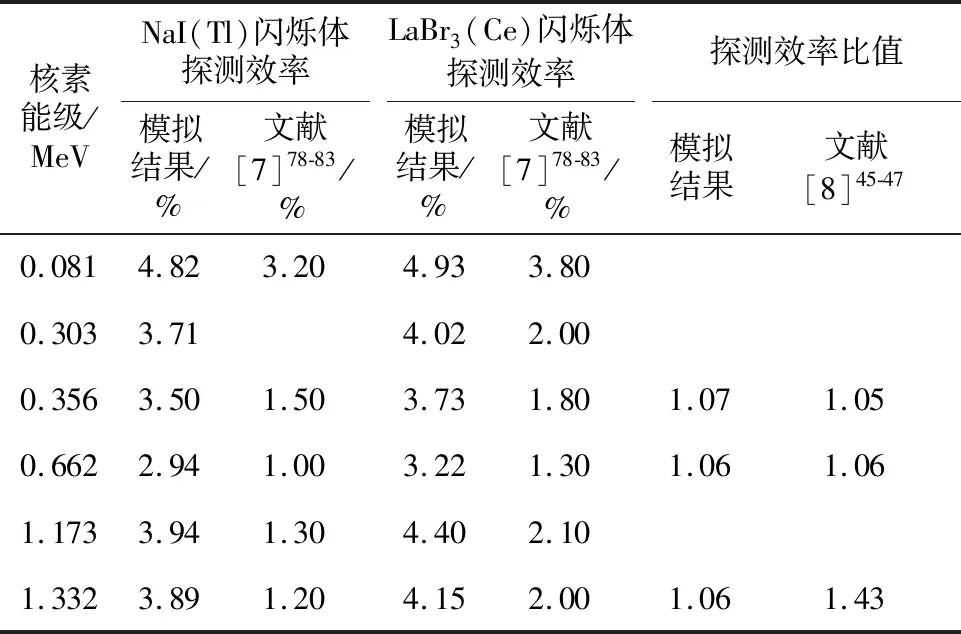
表3 探测器探测效率

注：源与探测器之间的距离为2 cm，其他均为5 cm。

从表3可以看出，试验模拟得到的探测器探测效率与文献试验中得到的数据相差较大。分析认为，这是由于：1)实际试验中存在大量的放射性自然本底，在统计全能峰的计数时，需要扣除大量的本底，从而造成真实事件的丢失；2)实际试验中电子学仪器存在时间响应问题，即死时间，也会造成一定的数据丢失。在本模拟试验中，这2种情况对试验的影响非常小，所以模拟得到的探测效率结果与试验数据相比偏大。但是，2种探测器探测效率的比值与文献[8]45-47中的测试数据符合的非常好，这说明本模拟试验结果是可信。同时，由于本模拟结果可以真实的反应探测器的探测效率，所以试验得到的模拟结果可以用于不同几何条件下闪烁体探测器对不同能量的γ光子的探测效率的修正。

4 结论

利用NPTool模拟代码，编写了可以对闪烁体探测器进行试验模拟的程序代码，对NaI(Tl)和LaBr3(Ce) 2种闪烁体进行计算机模拟，并将模拟结果与试验测试数据进行了对比。在探测器能量分辨率方面，模拟结果与试验测试数据吻合的较好。模拟试验中开创性的将探测器的能量分辨率设置为动态函数，随入射γ射线能量的不同而变化。这虽然增加了计算机的计算量，但是提高了模拟精度，可以为试验测量过程中探测器的刻度提供帮助。在试验测量中，利用计算机试验模拟，研究代码可以为不同几何形状的探测器的设计提供支持，也可以为探测器探测效率提供校准。

总体来说，二次开发后的NPTool模拟代码不仅可以对7.62 cm×7.62 cm尺寸的圆柱形闪烁体探测器进行高精度的模拟计算，也可以对理想尺寸和形状的闪烁体探测器进行试验模拟，为更加复杂的闪烁体探测器的探测器设计、γ能谱的测量分析提供一个简单便捷的试验工具。