一种利用ILSP的同步DS-CDMA信号快速盲解扩算法

张花国，曾 辉，尤少钦

(1．电子科技大学信息与通信工程学院，成都 611731；2. 气象信息与信号处理四川省高校重点实验室，成都 610225；3. 电子科技大学网络空间安全研究中心，成都 611731)

0 引 言

直接序列扩频(Direct sequence spread spectrum,DSSS)是现代通信系统中最常用的通信技术之一。在信号发送端将信息码序列与一个高速率的扩频码序列相乘，使得信号频谱扩展，可降低传输信号的功率谱密度，具有低截获概率特性。DSSS通信系统合作接收方，利用已知的扩频序列对接收信号合作解扩，可抑制干扰并恢复出传输信息[1-6]。针对DS-CDMA信号，不同用户使用不同的扩频序列，且各用户之间的扩频码序列相互正交，使其具有多址特性。DS-CDMA信号具有截获概率低、抗干扰能力强、码分多址等优点，被广泛应用于民用、军事通信和卫星通信等领域[7-9]。

对于非合作接收方，如电子对抗、频谱监视、认知无线电等场景，需要事先完成扩频序列的估计，再利用该估计扩频序列完成信号的盲解扩。对于单用户DSSS信号的盲解扩，目前学术界已经开展了较为充分的研究。针对扩频码周期与信息码周期之比为非整数的情况，文献[10]提出了一种基于差分主元分析(D-PCA)的扩频码估计方法。而针对扩频码周期与信息码周期之比为整数的情况：文献[11-12]对接收到信号的矩阵模型进行奇异值分解，由最大奇异值对应的左奇异向量估计得到扩频码序列；文献[13]对接收信号的样本协方差矩阵进行特征分解，由最大特征值对应的特征向量可准确估计出信号的扩频码序列；文献[14]先估计出接收信号的PN码序列，然后利用信息码剥离算法估计得到原始PN码序列。

针对多用户DSSS信号的盲解扩问题[15]，文献[16]提出了一种可逆跳跃的马尔科夫链蒙特卡罗(RJ-MCMC)扩频序列和信息序列联合估计算法；文献[17]利用改进二阶统计盲辨识(Second order blind identification，SOBI)算法估计出多用户短码DSSS的PN序列；文献[18]则采用了子空间分解和(Multiple signal classification,MUSIC)算法；文献[19-20]采用了目前较为有效的基于EM(Expectation maximization)算法的盲解扩算法。EM算法主要包括样本协方差矩阵的计算,并对其进行特征值分解及高斯混合分布模型的极大似然估计两部分。但基于EM算法的盲解扩算法的计算复杂度随用户个数的增加会呈指数增长，这是解决多用户问题时所不希望看到的。

本文针对该问题，提出了一种利用ILSP[21]的快速盲解扩算法。本文算法首先对信号样本协方差矩阵进行特征分解，得到由各用户扩频码序列张成的信号子空间估计，然后根据得到的信号子空间估计矩阵和扩频码的有限符号集特性，利用ILSP算法得到扩频码矩阵的估计。估计出扩频码矩阵后，进一步对信号解扩得到信息码矩阵估计，完成同步DS-CDMA信号的盲解扩。本文算法利用迭代最小二乘算法来估计扩频码矩阵，每次迭代过程将前一次的估计值作为新的初始值进行迭代，直到最后收敛或达到最大迭代次数为止，因此计算复杂度不会随用户个数增加而呈指数增加。

1 信号模型

本文使用的信号是同步短码DS-CDMA信号，假设扩频码周期L、信息码元速率等信号信息都已估计得到[22-23]，用户个数R也已通过信息论MDL(Minimum description length)准则[24]估计得到。本文与文献[11-12,14-22,25-26]相同，仅考虑基带DS-CDMA信号，非合作场景条件下信号载频的精确估计可由文献[13]中所提出的方法实现。

非合作接收方截获到的同步DS-CDMA信号经码元速率采样后可写为：

(1)

式中:R为用户个数；Ar为第r个用户的信号幅度；M为信息码个数；br为第r个用户的采用BPSK调制的信息码序列，即br(m)∈{±1}，其中m的取值为0到M-1；cr为第r个用户的扩频序列；v(n)为方差为σ2的高斯白噪声。

非合作场景下实现DS-CDMA信号的盲解扩，需要事先完成信号检测、参数估计、盲同步、扩频码序列提取等完整过程，而本文研究的重点是低信噪比条件下扩频码序列的快速估计问题，因此本文假定信号已完成盲同步，即各用户传输符号的起始位置已通过协方差矩阵Frobenius范数最大化法[13,20]估计得到。本文与文献[19]相同仅考虑瞬时信道的环境，对于移动通信领域往往存在严重的多径效应，但对于卫星通信信道却可以忽略多径效应的影响，因此，本文所提出的算法可用于实际非合作卫星通信信号处理领域。

2 快速盲解扩算法

对于同步DS-CDMA信号，信号模型可以写成如下矩阵形式:

Y=CABT+V

(2)

式中:L×R维矩阵C为扩频码矩阵；A=diag(A1，A2,…,AR)为信号幅度对角阵；M×R维矩阵B为BPSK调制的信息码矩阵；V为方差为σ2的高斯白噪声矩阵。

由式(2)可得到信号协方差矩阵为：

R=E[YY]=CA2CH+σ2I

(3)

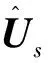
具体实现步骤为：

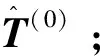
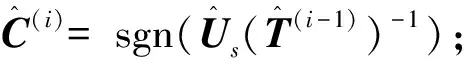
(4)重复步骤(2)～(3)直到算法收敛或达到最大迭代次数，算法收敛的条件为：

其中,ε为收敛的门限值，通常取为1×10-9；在本方法中，最大迭代次数设为50。

(5)为了提高算法性能，重复步骤(1)～(4)多次(本方法选为40)，选择迭代效果最好(τ最小)的一次作为最终结果。

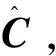
3 计算复杂度分析

基于EM算法的盲解扩算法的计算复杂度主要集中在样本协方差的特征分解和高斯混合分布模型的极大似然估计两部分。其计算复杂度分别为O(L3)和O(2RR2M)，其中L为扩频码周期，R为用户个数，M为信息码个数[26]。可见，随着用户个数的增加，基于EM算法会使计算复杂度指数增加，这对于解决多用户问题十分不利。本文算法与基于EM算法一样也需要对信号样本的协方差矩阵进行特征分解，其计算复杂度为O(L3)。在得到信号子空间估计之后，为了消除特征分解产生的酉矩阵模糊，本文提出利用ILSP算法来实现。由上一节算法过程的分析可知，本文算法计算复杂度主要集中在步骤(2)和步骤(3)：其中步骤(2)求模糊矩阵的逆的计算复杂度为O(R3)，矩阵乘法的计算复杂度为O(R2L)，由于L>R，因此步骤(2)的总计算复杂度为O(R2L)；步骤(3)的计算复杂度等于求矩阵伪逆的计算复杂度，即O(R2L)，故步骤(3)的总计算复杂度也为O(R2L)。因此利用ILSP算法来实现需要的计算复杂度为O(R2L)。由上述分析可知，本文提出算法虽然随用户个数增加，计算复杂度也会增加，但不会像EM算法那样急剧增加。因此，对于用户个数较多，扩频码周期不大的同步DS-CDMA信号，本文提出的算法在计算复杂度上有明显优势。

4 性能仿真

下面通过仿真试验考察算法的盲解扩性能，并与EM算法和扩频波形已知的合作通信解扩进行比较。考虑用户个数分别为R=3和R=6，扩频波形周期L=31的同步短码DS-CDMA信号，信息码个数M=100，信噪比变化从-15 dB到-7 dB变化，通过1000次蒙特卡罗仿真实验得到信号误码率随信噪比变化的曲线图如图1所示。从图中可以看出，本文算法仿真结果与EM算法基本一致，随着信噪比的增加，算法逐渐逼近合作通信解扩，从而证明本算法的有效性。

在用户数、扩频波形周期相同的情况下，固定信号信噪比为-10 dB时，信息码长度从20～300变化，通过1000次蒙特卡罗仿真试验得到信号误码率随信息码长度变化曲线图如图2所示。从图中可以看出本文算法仿真结果与EM算法基本一致，随着信息码个数的增加，算法逐渐逼近合作通信解扩，从而证明本文算法的有效性。

在扩频波形周期L=31，信噪比固定为-5 dB时，信息码个数M=100，用户个数从2～6变化，仿真使用计算机为主频2.7 GHz、内存6 GB的台式计算机，经过1000次蒙特卡罗仿真实验得到的算法运行时间与用户个数变化曲线图如图3所示。图3为本文算法运行消耗时间随用户个数变化曲线和EM算法的对比图。

从图3中可以看出本文算法虽然随用户个数增加迭代时间也增加，但是并不会像EM算法那样剧烈增长，并且可看出本文算法相比于EM算法，运行时间明显降低。

CDMA信号各用户采用相同的工作频率，尽管非合作场景下采用文献[10]方法可实现信号频率的估计，但低信噪比条件下仍然存在一定的频率估计误差。下面考察本文方法在存在频率估计误差情况下的盲解扩性能。假定用户个数为3，其它仿真条件与图1相同，各用户在不同频率估计均方根误差(Root mean square error，RMSE)条件下的盲解扩性能如图4所示，其中每次蒙特卡罗仿真试验中，每个用户的频率误差由标准差为RMSE的高斯分布独立随机产生进行模拟。

由仿真图4可看出，随着频率估计误差的增大，本文所提出方法的盲解扩性能将会下降，但当频率估计RMSE较小时，本文提出方法与无频率估计误差时具有相近的性能，因此，本文方法在存在微小频率估计误差时具有一定的适应性。

5 结 论

本文从同步短码DS-CDMA信号的数学模型出发，首先通过对信号的协方差矩阵进行特征分解，估计出由信号扩频序列张成的信号子空间，然后根据估计得到的信号子空间矩阵和扩频码序列的有限符号集特性，利用ILSP算法消除由特征分解带来的酉矩阵模糊问题，得到信号的扩频序列矩阵估计，最后利用估计得到的扩频序列矩阵估计得到信息码矩阵，完成盲解扩。通过计算机仿真校验了本文算法在用户数较多，扩频码周期较小时，相对于EM算法有较低的计算复杂度，而且盲解扩性能也与EM算法相当。