改进布谷鸟搜索算法优化支持向量机的MEMS陀螺温度零偏补偿

高 策， 沈晓卫, 章 彪, 胡豪杰

(1.火箭军工程大学研究生院，西安 710025; 2.火箭军工程大学核工程学院，西安 710025)

0 引 言

微机电系统(Micro-electro-mechanical system，MEMS)陀螺具有成本低、体积小、易于集成等特点，已经在汽车工业、自动化、机器人等领域得到了广泛的应用[1-2]。同时，MEMS陀螺的主要材料是薄硅片，硅具有许多不同于宏观条件下的物理和机械性能[3]。当温度发生变化时，陀螺不仅在结构尺寸上发生改变，材料的弹性模量拉伸强度残余应力和外围电路的电子器件性能也发生变化，造成MEMS陀螺的零偏曲线往往具有非线性和随机性[4]。因此，为了进一步提高惯性导航系统中MEMS陀螺的精度和性能，建立MEMS陀螺零偏的有效温度模型，并进行补偿，减少温度对微机械陀螺零偏的影响是绝对必要的。

针对MEMS陀螺零偏温度补偿算法很多学者进行了研究，常用的方法是最小二乘分段法、BP神经网络、支持向量机等。文献[5]通过最小二乘拟合计算每个温度项的系数建立模型，得到温度补偿曲线。然而，最小二乘分段拟合当分段间隔较小时，计算参数多，计算量大；分段间隔较大时，拟合精度较低，分段间隔处存在较大振荡。文献[6-7]应用BP神经网络与数理统计相结合建立温补模型，文献[8]选择RBF神经网络对光纤陀螺进行温度漂移辨识，均有效改善陀螺零偏稳定性。神经网络具有很强的并行处理、自学习和自适应能力。然而，其结果难以得到较好的泛化性能，难以避免过度拟合或欠拟合的问题。除此之外，神经网络存在容易陷入局部优化的危险。

由Vapnik及其同事开发了一种基于统计学习理论(Statistical learning theory, SLT)的新型学习机，称为支持向量机(Support vector machines, SVM)，它实现了结构风险最小化(Structure risk minimization, SRM)原理[9-10]。文献[11]提出一种蚁群算法优化最小二乘支持向量机的误差补偿模型，有效提高陀螺精度，但该方法主要应用在高精度的光纤陀螺上。支持向量机能够克服上述典型的神经网络方法的缺点，它具有以下的特点：(1)支持向量机的训练相当于解决一个二次规划问题，从而产生一个独特的全局最优解;(2)通过使用内积和内核函数有效地解决非线性问题。因此，SVM已经应用于模式识别、回归预测和非线性控制等领域[12-14]。

CS算法的主要优点是参数少，操作简单，容易实现，搜索随机路径的能力强。尽管该算法已经在许多领域得到了应用，但仍存在一些不足。最优解受到固定检测概率的影响；Levy flight飞行机制通过交替大步骤和小步骤来提高全局搜索能力，但缺乏自适应性造成难以在收敛速度和搜索能力之间的平衡。为了解决上述问题并且有效提高MEMS陀螺零偏温度补偿精度，提出了一种基于改进布谷鸟搜索算法(Cuckoo search, CS)优化的支持向量机温度建模方法。

1 基于SVM的MEMS陀螺温度零偏误差建模补偿

MEMS陀螺的温度零偏误差补偿问题是确定陀螺输出值和温度的对应关系，本质上是函数拟合问题。并且两者的函数关系很难依据理论方法进行准确建模。一般函数f(x)的表达式只能根据样本数据(x1,y1),(x2,y2),…,(xk,yk)求解。xi表示陀螺温度，yi表示陀螺输出值。

1.1 支持向量机函数拟合方法

SVM采用如下式(1)的形式对未知函数f(x)进行拟合逼近：

y=f(x)=wTφ(x)+b

(1)

式中：待拟合函数的自变量和因变量分别为x∈Rn,y∈R,b为偏置项，φ(·)为将自变量从低维空间向高维空间映射的特征函数，上式主要是先将非线性函数从低维空间映射到高维空间，然后进行线性拟合。

将未知函数拟合问题转换为函数R的最小化问题：

(2)

式(2)的函数最小化问题是一个凸二次优化问题，因此引入拉格朗日函数：

(3)

式中：ai,ai*≥0,γi,γi*≥0,i=1,2,…,k。式(2)中求函数R的最优解的问题转化为求式(3)的鞍点问题，在鞍点处，函数L是有关w,b,ξ,ξ*的极小值点，并且是有关a,a*,γ,γ*的极大值点。从而，将式(5)的最小化问题转换为求式(3)对偶问题的最大问题，即：

(4)

在鞍点处，拉格朗日函数L是有关w,b,ξ,ξ*的极小点，因此：

(5)

对于支持向量机非线性回归，可以分为三步:第一步，把数据从低维空间映射到一个高维特征空间，即x→φ(x)；第二步，在高维空间进行线性回归；第三步，根据第二步的结果取得在原空间非线性回归的效果，并且引入符合Mercer条件的核函数k(xi,xj)=φ(xi),φ(xj)〉,运算符代表对于核函数的选择。即：

(6)

此时：

(7)

对于支持向量机的方法，选用不同的核函数k(x,xj)，就可构成不一样的支持向量机。其中应用最为广泛的式径向基核函数，径向基核函数是局部性强的核函数。相比其他核函数的径向基核函数适用于小样本和大样本，高维和低维的情况；与多项式核函数相比，径向基核函数参数少，函数复杂程度低，计算量小。所以在本文提到的方法中，选用径向基核函数如式(9)所示：

(9)

式中：σ2是径向基函数的核宽度。

1.2 改进布谷鸟算法参数寻优

采用SVM方法做非线性函数拟合，效果很好。但用SVM做非线性拟合的时需要调节相关的参数(主要是惩罚参数C、核函数参数σ以及不敏感系数ε)才能得到较好的精度。采用CS的方法寻找最优参数，可以有效避免过学习和欠学习状态的发生，最终得到较理想的准确率。

1.2.1布谷鸟算法

布谷鸟搜索算法是计算智能领域，除了蚁群算法、鱼群算法之外的一种群体智能的优化算法，该算法最早是由Yang和Deb在2010年提出的[15]。其受到鸟类的两种特殊行为的启发：布谷鸟的寄生行为和果蝇的Levy flight飞行行为。它着重于三个理想化的规则[16]：

1)每只布谷鸟每次只产一个蛋，并将蛋放入随机选择的巢中；

2)产蛋质量最好的巢穴会传给下一代；

3)可用宿主巢的数量是固定的，并且宿主鸟发现布谷鸟放置的卵的概率Pa∈[0,1]。在这种情况下，寄主鸟可以将蛋扔掉或放弃巢，并建立一个全新的巢。

布谷鸟巡找巢穴和位置更新的公式为：

(10)

1.2.2检测概率的动态调整策略

在CS算法中，是否产生新个体由随机数ε和检测概率Pa的比较结果决定。最优解的搜索结果受Pa数值的影响：当Pa太大时，较好的巢位很难收敛到最优位置；相反，当Pa太小时，它会遇到当前坏窝位置的慢速收敛。根据自然界的周期性变化，我们在CS算法中引入了周期变异算子来调整被检测概率(Pa)。本文将余弦循环算子引入CS算法实现Pa的周期性变化。

(11)

其中,T是周期算子的周期；t是当前迭代次数；Pa,max和Pa,min是Pa的动态控制参数，分别等于0.75和0.1。

1.2.3步长的动态调整策略

通过分析原始CS算法，可以看出CS算法的步长对全局最优解和搜索精度有显着影响。较大的尺寸有助于算法跳出局部最优状态，但会降低收敛精度和收敛速度。另一方面，步长较小时，获得局部最佳结果非常容易。因此，关键是如何获得合适的搜索步长，以避免局部最优解，并提高收敛速度和收敛精度。本文提出了一种自适应布谷鸟搜索算法，该算法通过最后一次最优嵌套生成和当前迭代次数的组合信息对步长进行调整。

根据当前的优化进程，即迭代次数与最大迭代次数的关系，布谷鸟搜索步骤S设置如下：

(12)

式中:m∈(0,1)是调节因子；Ei-1是上一代群体的最佳巢位；h∈[0,1]是限制因素；t和tmax是当前迭代次数和最大迭代次数；Smin是最小的搜索步骤；p是1～30的整数。

1.2.4算法实现

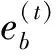
(13)

1.3 MEMS陀螺零偏误差建模与求解

通过大量的陀螺温度实验获取的温度误差样本数据，利用本文提出的基于CS优化SVM参数的方法对微机械陀螺的温度误差进行建模。该过程包括以下3个步骤：

1)数据归一化

为了加快参数寻优的速度以及模型训练的效率，同时，为了优化内存空间，可以用式(14)对样本数据进行归一化处理：

(14)

式中：y表示归一化后输出的值，ymax=1,ymin=-1；x表示归一化前的输入得值，xmax为输入数据的最大值，xmin为输入数据最小值。通过式(14)可以将任意实数范围内数据变换到[-1，1]的区间内。

2)改进布谷鸟算法优化SVM

以实验数据为训练数据对SVM的惩罚参数C、核函数参数σ以及不敏感系数ε进行寻优。

3)模型训练

根据基于CS优化SVM参数方法的拟合原理，将第二步基于布谷鸟法调优的参数寻优结果和第一步归一化后数据代入支持向量机函数进行训练，得到最佳拟合函数，即：

(15)

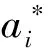
2 实验分析

为了研究温度对MEMS陀螺零偏的影响，将微机械IMU放在高低温箱的水平台上(如图1所示)，将环境温度从-30 ℃开始以1 ℃/min的速率逐渐升温至70 ℃(如图2所示)。在微机械陀螺的工作过程中，以50 Hz的频率实时输出陀螺值量测数据以及温度数据。同时，由于微机械陀螺的输出数据具有较大的量化噪声，无法直接用于温度误差的标定，因此，采用20 s数据(即1000组)平滑后的结果作为温度误差建模的样本点，温度数据同样进行20 s 平滑处理。陀螺温度误差经20 s平滑后的曲线如图3所示。

分别应用传统的最小二乘分段拟合算法、BP神经网络以及基于CS的SVM算法对微机械陀螺零偏输出进行辨识。参数设置如表1、表2所示。利用三种方法辨识得到的数据对温度变化下微机械陀螺的零偏进行补偿，补偿效果如图4～6所示。

表1 最小二乘方法和BP神经网络方法参数设置Table 1 Least square method and BP neural network method parameters set

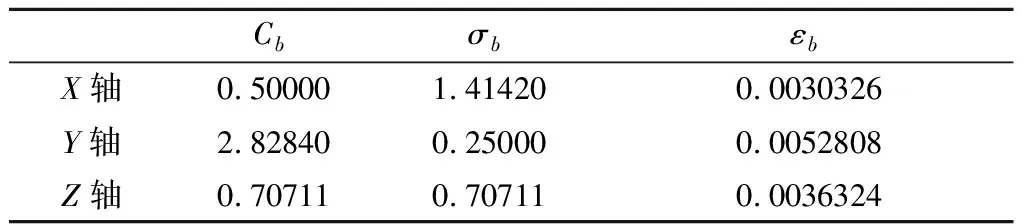
表2 基于改进CS优化SVM的最佳参数Table 2 Optimization of SVM based on CS

从图4～6可以看出,三种方法对微机械陀螺的温度误差都起到了减小的作用，但效果不同。将补偿后三种方法得到陀螺误差进行比较，如图7～9所示。

从图7～9可以看出,基于改进CS的SVM方法补偿后的数据稳定性明显高于其他两种方法，BP神经网络和本文方法明显优于最小二乘分段拟合方法，并且对于误差曲线斜率变化大的地方(如Z轴0 ℃～10 ℃)本文方法稳定性比BP神经网络方法更好。进一步统计温度补偿后数据的最大误差和方差，结果如表3所示。可以看出，采用基于CS的SVM的补偿方法的方差比最小二乘平均减小约63.2%，最大误差平均减小约71.63%，并且比基于BP神经网络补偿方法的方差平均减小约43.4%，最大误差平均减小约48.3%；从表4可以看出本文方法量化噪声Q、零偏不稳定性B、角速率随机游走K相比其他两种方法都降低了一个数量级，角度随机游走N、速率斜坡R也有明显下降，从而证明本文方法的精度更高，优越性更强，提高了MEMS陀螺对环境的适应能力。

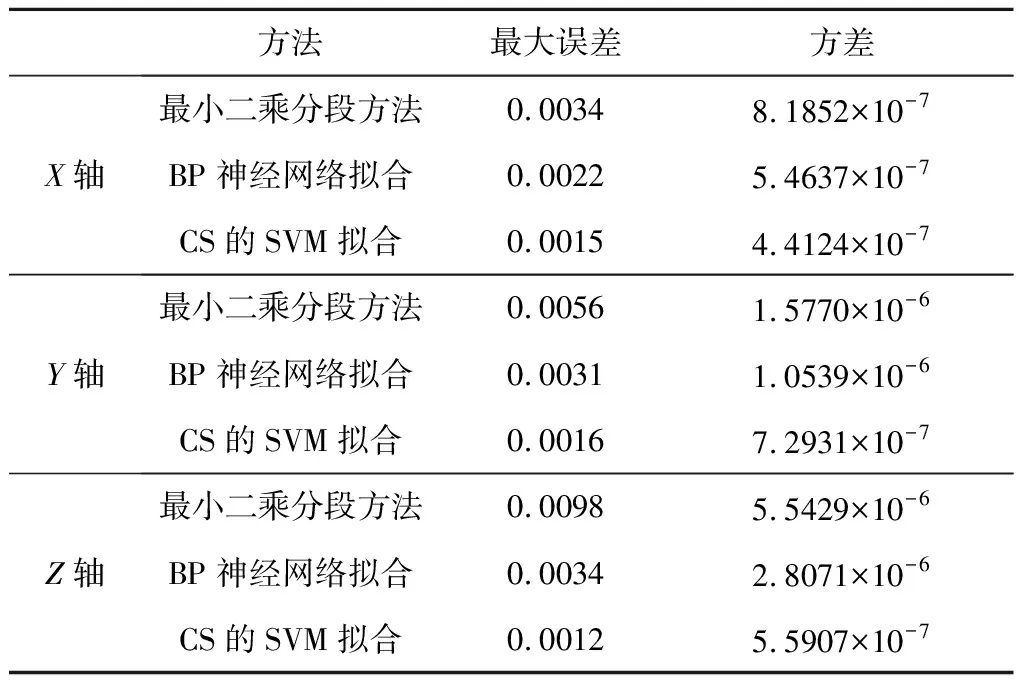
表3 各种方法补偿后的最大误差和均方差比较Table 3 Various methods of gyro output after the average and the mean square error comparison

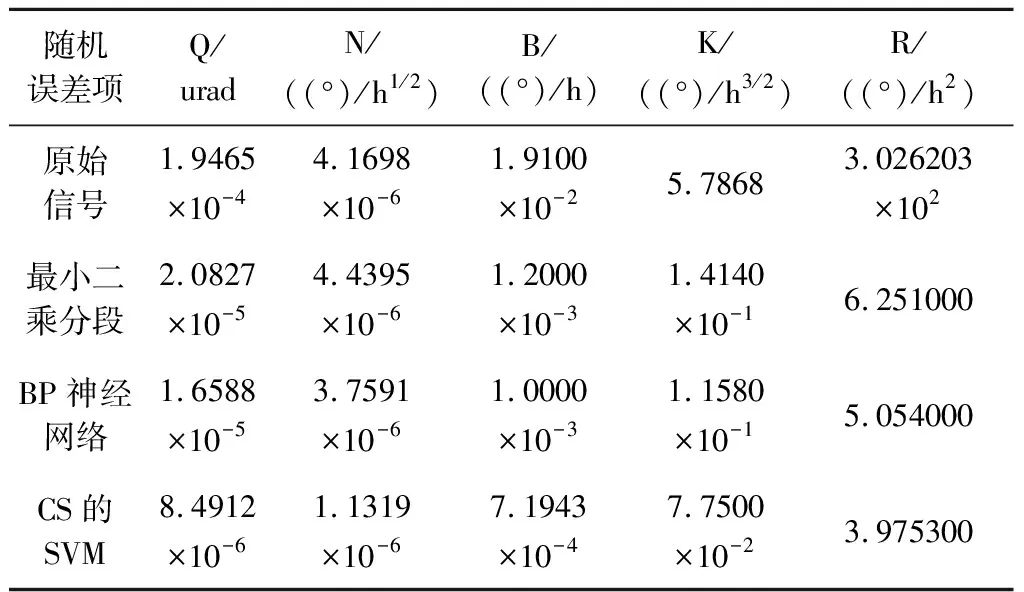
表4 Y轴微机械陀螺的原始信号和随机误差的Allan方差分析比较结果Table 4 Allan variance analysis results of original signal and random error of Y-axismicromachined gyroscope

动态条件下(温度25 ℃)，将微机械陀螺仪放置在转台上，使转台以5 (°)/s的恒定速率旋转，采集60 s的数据进行温补验证，如图10所示。从图中可以看出，利用本文方法对陀螺零偏进行温度补偿后，陀螺的输出值更加精准有效。

3 结 论

为了降低微机械陀螺仪的温度漂移，本文提出了一种基于改进CS调节SVM参数的建模与补偿方法。首先，用于建模的温度漂移数据采用20 s数据(即1000组)平滑预处理。然后采用支持向量机构造漂移模型。改进CS方法用于优化支持向量机的参数，提高了建立模型的精度。通过大量的温度试验检验了方法的有效性。结果表明，与最小二乘方法、BP神经网络方法相比，CS调节支持向量机的补偿数据方差分别平均减小了63.2%，43.4%，最大误差分别平均减小71.63%，48.3%。