基于变结构控制的无人机编队飞行方法

张西勇，叶慧娟

(1.武汉东湖学院 机电工程学院， 武汉 430033; 2.海军工程大学 兵器工程学院， 武汉 430033)

在现代战争中，无人机(UAV)由于具备零伤亡的优势，已经成为执行作战任务的重要装备。针对作战任务的复杂性和多样化，往往需要多个UAV协同执行任务，无人机编队控制问题亟待解决。

当前，无人机编队控制问题已经成为无人机领域研究的热点，国内外均已开展大量的研究工作。美国国防高级研究项目局(DAR-PA)资助的MICA项目，其研究重点是提高UAV的自主控制和协同控制能力[1]；Galzi采用连续高阶滑模控制方法设计了编队控制器，对外界干扰有一定的抑制能力[2]；景晓年等人利用图论相关知识和多智能体系统一致性理论建立了集群运动的控制模型[3]；朱熠等人基于鲁棒最优理论和动态投影方法设计了动态投影控制系统[4]。沈佩珺对小型高速无人机及其协同编队控制进行了研究，采用改进的鲁棒LQR结合模型参考自适应为无人机进行了控制律设计[5]。

本文在长机和僚机相对运动方程的基础上推导视线角变化的状态方程，通过设计变结构控制器控制视线角在某固定值，从而实现了无人机的编队控制。

1 建模

针对不同的作战任务需求，经常需要多个无人机集群式执行作战任务，如何保证多个无人机按照设定的队形稳定飞行，而不会发生碰撞，无人机的编队控制问题就显得非常重要。无人机经常使用的飞行编队有领航-跟随编队和左右菱形编队。本文以左右菱形编队为研究对象，以长机和僚机相对运动关系为基础建立控制对象的状态方程，并在此基础上进行控制器设计。

编队飞行的平面几何关系如图1所示。

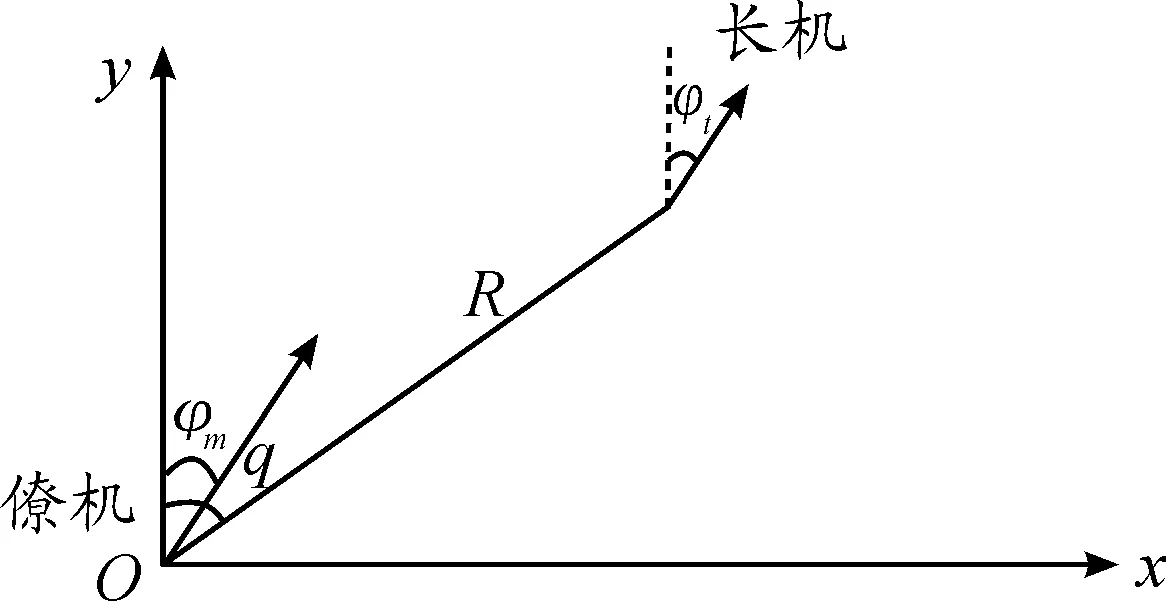
图1 长机与僚机相对运动的平面几何关系

在oxy平面，长机和僚机的速度大小相同，只要保证长机和僚机视线角q控制在某个角度并保持恒定，则能保证长机和僚机的队形保持不变。

长机和僚机在oxy平面内的相对运动关系可用式(1)来完整描述：

(1)

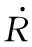
为了便于进行控制器设计，首先通过相对运动方程，如式(1)所描述，推导长机和僚机视线角q变化的状态方程，推导过程如下。

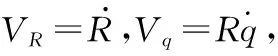
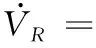
(1)

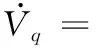
(2)

令:

(4)

(5)

(6)

(7)

把式(4)～(7)代入式(2)和式(3)，得到

(8)

(9)

(10)

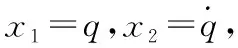
(11)

2 控制器设计

由于变结构滑模控制具有鲁棒性好，抗干扰能力强的优点，本文采用变结构控制对控制量uq进行控制器设计。由于控制目标是将视线角q，即x1控制在45°角并保持恒定，所以取滑模面：

(12)

由于取参数c>0，在滑模面上s=0，视线角x1=q稳定地趋于45°角。

选取Lyapunov函数V=s2/2,将V相对于时间微分得到：

取控制：

则

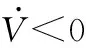
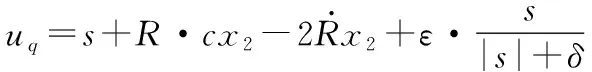
至此，无人机编队控制器的设计及其理论证明已完成，下面进行仿真分析，验证控制器的有效性。

3 仿真分析

通过前面主机和僚机相对运动方程，系统状态方程及控制器方程，建立联立方程组如下：

(13)

方程组(13)中7个未知数，7个方程，其中速率V为常数，方程组存在唯一解。采用四阶龙哥库塔法求方程组的数值解。初始条件如下：主机和僚机速度均为V=30 m/s， 初始视线角35°，主机初始航向角25°，僚机初始航向角15°，主机与僚机间初始距离100 m，取常数c=2，ε=10，σ=0.01仿真步长为0.001 s，仿真时间30 s。仿真结果如下：

从仿真结果(见图2、图3、图4、图5和图6) 可以看出，初始时刻主机与僚机间视线角为35°，不符合编队队形45°地要求，在控制器作用下僚机调整航向角，使得主僚机间视线角迅速调整到45°，并保持稳定。当主机与僚机间视线角控制在45°后，主机与僚机间距离保持不变，整体队形保持不变，达到了编队控制的要求。

本文所设计的控制器还具备强鲁棒性，下面以主机通过某障碍物作机动后保持恒定速度直飞的例子进行仿真验证。仿真中以主机航向角在初始一段时间内为时间的正弦函数来模拟主机作机动。

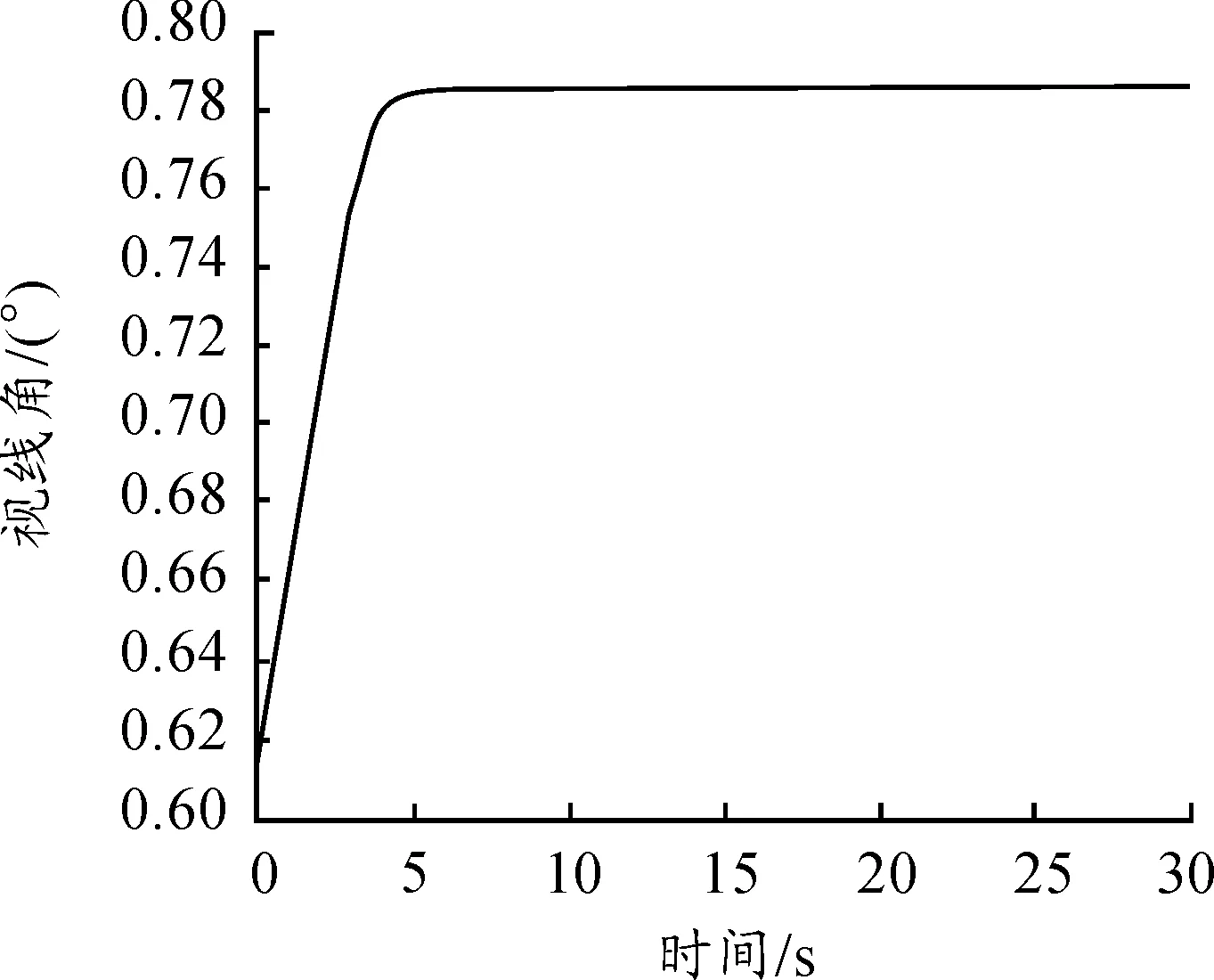
图2 主僚机间视线角

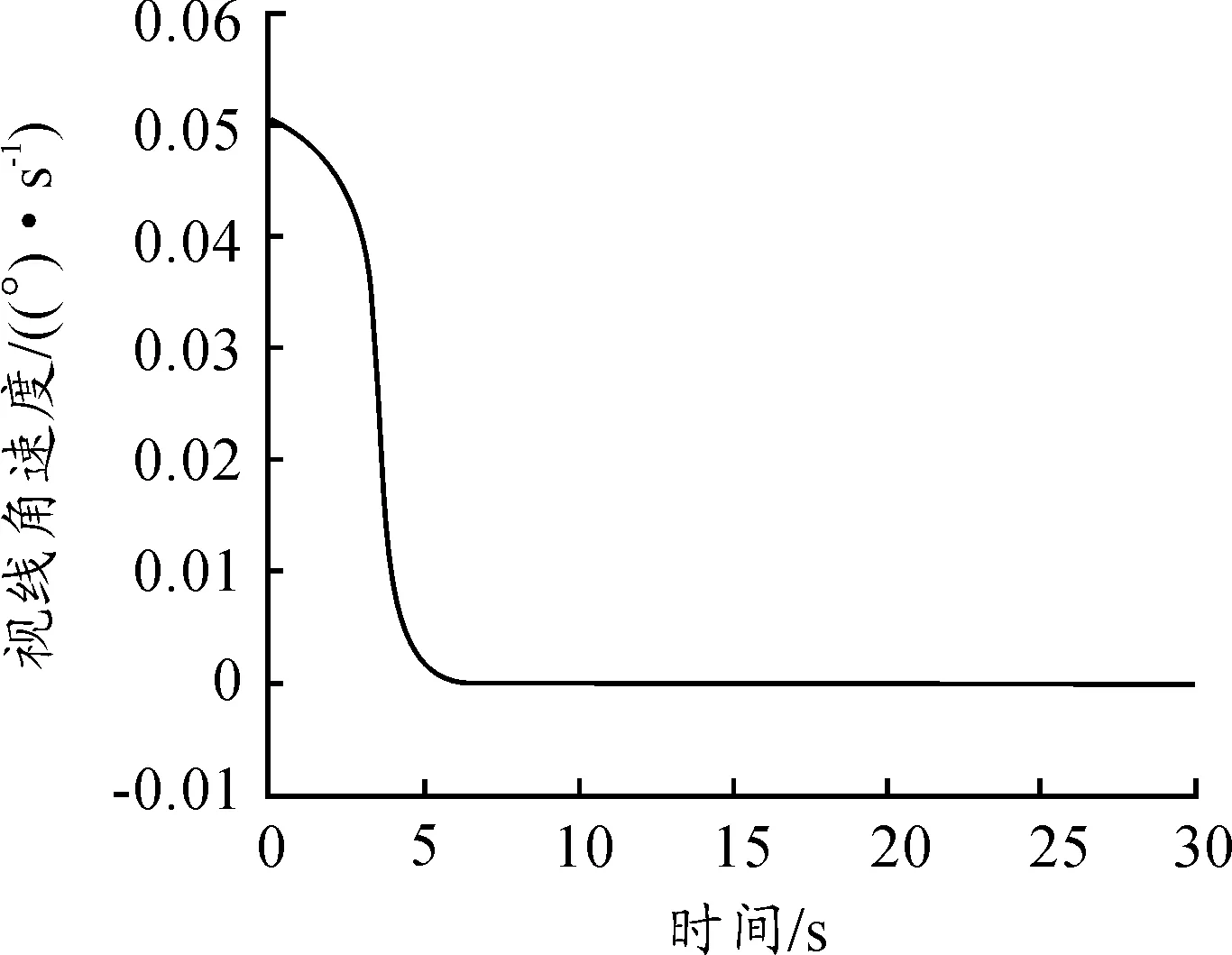
图3 视线角速度

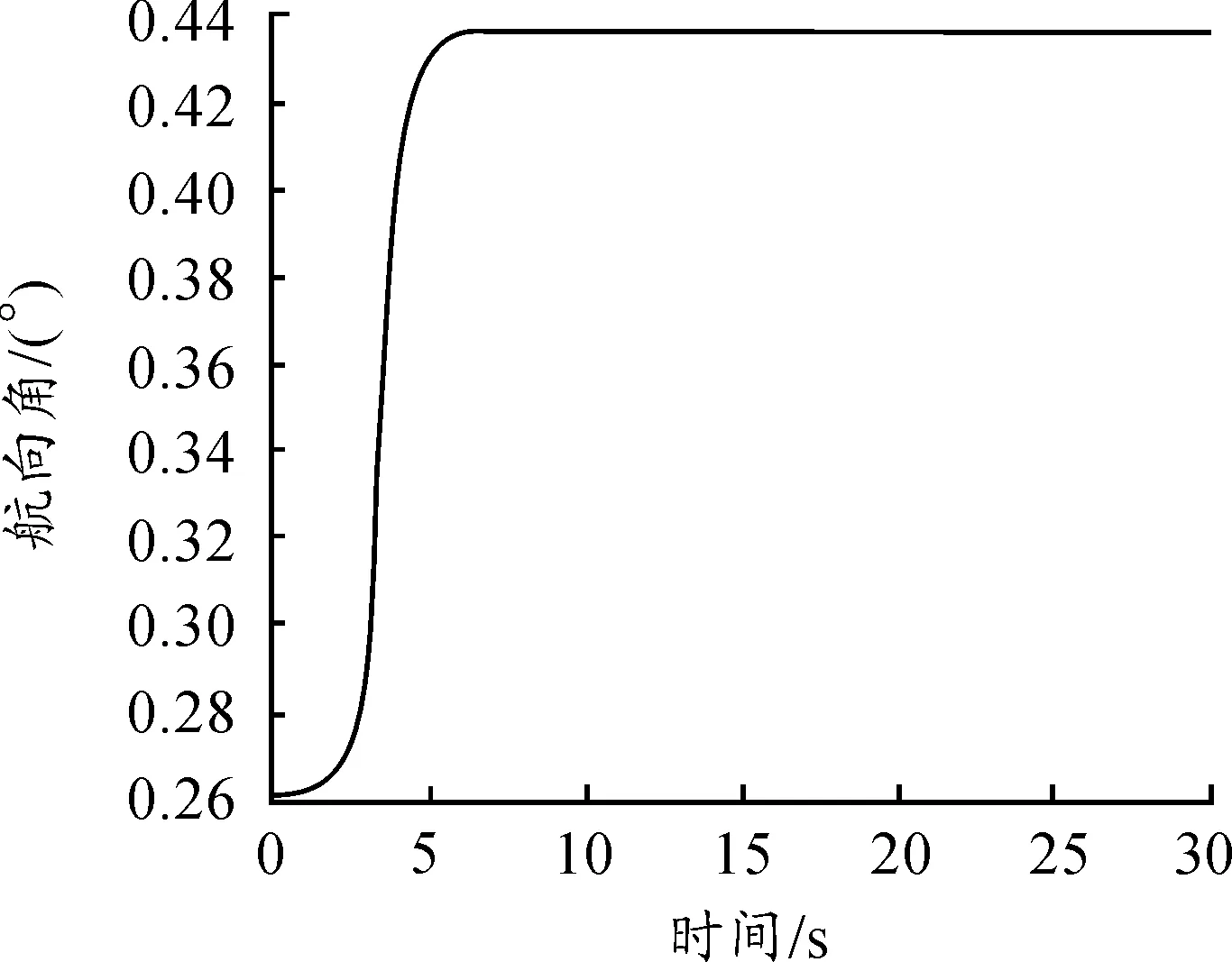
图4 僚机航向角

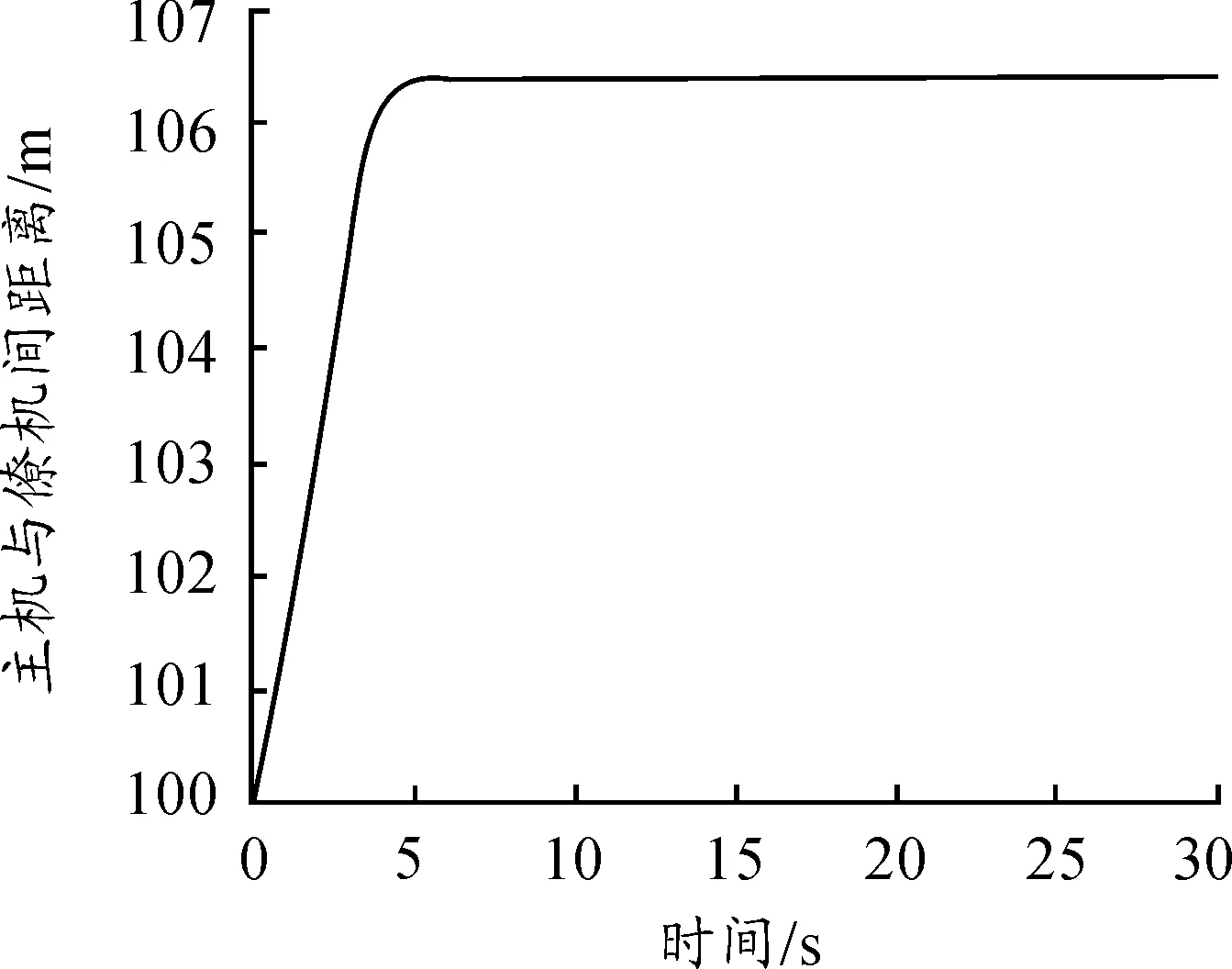
图5 主僚机间距离

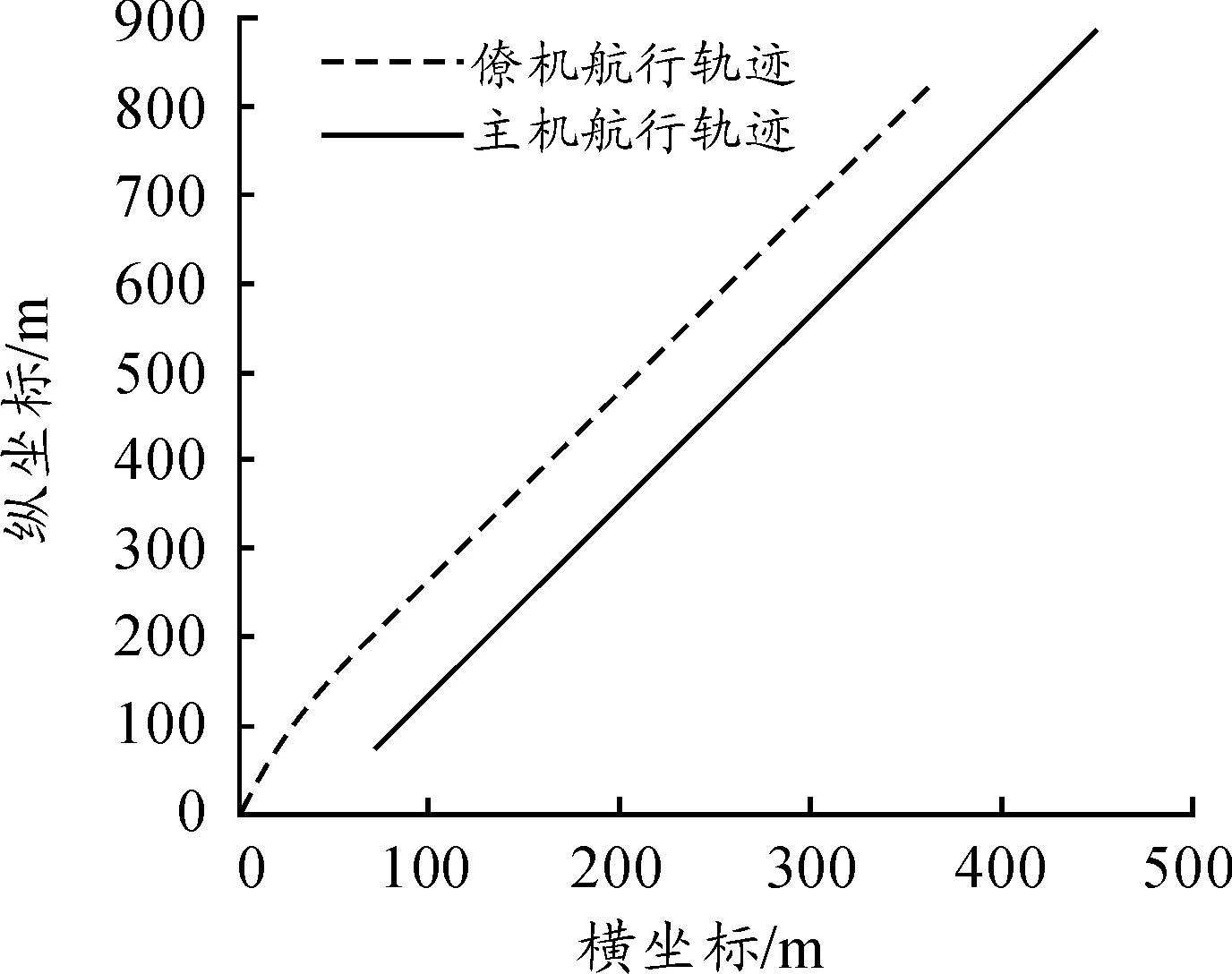
图6 主僚机运动轨迹

从仿真结果(见图7、图8、图9、图10和图11)可以看出，主机通过障碍物时航向发生变化，僚机在控制器作用下也紧跟着改变航向，尽可能保持队形不变，从而也随着主机绕过障碍物。主机与僚机绕过障碍物后，继续保持原来队形飞行。主机与僚机间视线角在绕过障碍物时存在波动，绕过障碍物后保持在45°。从前面控制系统建模过程可以看出，控制器将主机机动视作干扰处理，利用变结构控制的鲁棒性对干扰进行抑制，从而达到控制目的，仿真结果也正好验证了这一点，主机绕过障碍物时作机动改变不了控制器的稳定性。

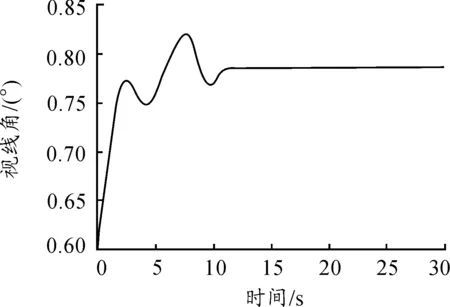
图7 主僚机间视线角

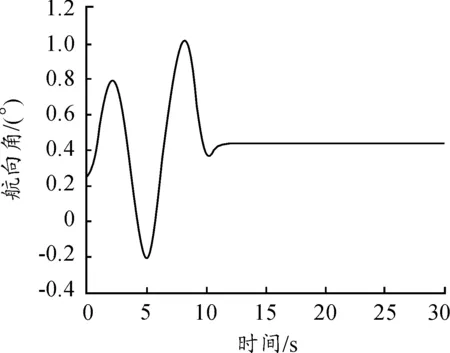
图8 视线角速度

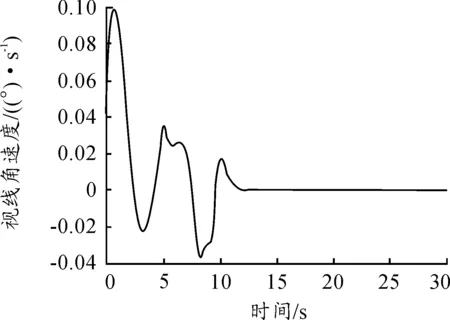
图9 僚机航向角

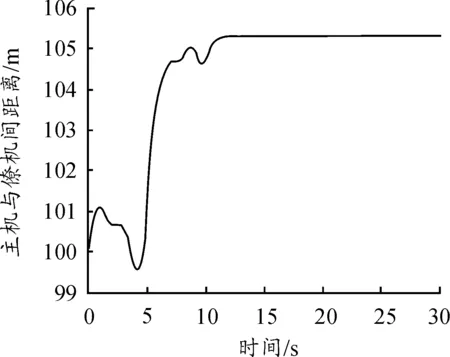
图10 主僚机间距离

图11 主僚机运动轨迹

4 结论

本文在只要能将主机与僚机间视线角控制在固定角度就能保证无人机队形保持不变的思想指导下，通过主机与僚机相对运动方程，推导主机与僚机视线角变化的状态方程，采用变结构控制方法设计控制器。理论推导和仿真表明：设计的控制器能够保证主机和僚机间的视线角控制在指定角，并且对机动具有强鲁棒性。