对数似然比置信传播算法的改进

郑娟毅 孙宇 张帆

摘  要： 改进对数似然比置信传播（LLR BP）算法，以提高其对低密度奇偶校验（LDPC）码的译码性能。在变量节点间加入信道响应相关性，并在算法中预设迭代次数，以使变量节点间传递的外部信息达到平衡，降低外部信息震荡现象，并保障译码不会因所需迭代次数过大而终止。改进型LLR BP算法可降低误码率，并在信噪比（SNR）较小时降低译码迭代次数。

关键词： 对数似然比; 响应相关性; 信息震荡; 迭代预设; 译码性能; 改进型LLR BP算法

中图分类号： TN911.22?34                        文献标识码： A                        文章编号： 1004?373X（2019）15?0005?03

Improvement of log?likelihood ratio belief propagation algorithm

ZHENG Juanyi， SUN Yu， ZHANG Fan

（School of Communications and Information Engineering， Xian University of Posts and Telecommunications， Xian 710121， China）

Abstract： Log?likelihood ratio belief propagation （LLR BP） algorithm is improved to enhance its decoding performance for low density parity check （LDPC） codes. The channel response correlation is added between variable nodes and the number of iterations is preset in the algorithm to balance the external information transmitted between the variable nodes， reduce the external information oscillation phenomenon， and ensure that the decoding is not terminated while the required number of iterations is too large. The improved algorithm can reduce the bit error rate and decrease the number of decoding iterations when the signal noise ratio is small.

Keywords： log?likelihood ratio; response correlation; information oscillation; iteration preset， decoding performance; improved LLR BP algorithm

0  引  言

随着人们对高速率通信不断追求，第五代（Fifth Generation，5G）移动通信技术将对人们的生活、学习、工作带来更多的便捷和改变，到目前已确定低密度奇偶校验（Low Density Parity Check，LDPC）码是5G采用的信道编码技术之一。LDPC码作为5G信道编码标准热门候选技术之一[1]，对提高LDPC码译码性能显得尤为重要。

通常所采用对数似然比置信传播（Log?likelihood Ratio Belief Propagation，LLR BP）算法对LDPC进行译码，相较于原始的置信传播（Belief Propagation，BP）算法，LLR BP算法由累乘转变为累加，大大降低了译码复杂度。但在译码性能上还需要进一步的提升，改进的LLR BP译码算法是在LLR BP算法[2]基础上加入响应相关性并在算法中预设迭代次数，使得LLR BP算法得到进一步改进。

1  LLR BP译码算法

LLR BP与BP译码算法思想一致，LLR BP采用对数似然比描述BP算法。这样就把乘法运算转变成加法运算，LLR BP算法的优点在于极大地减少运算量，使得译码复杂度得到了很大的降低。

通过将一个二值随机变量[x]引入LLR BP译码，其对数似然比[L（x）]定义为：

推导得完整的LLR BP算法步骤[2?3]如下：

1） 初始化：[vml=v0l];

2） [sm]更新：[uml=2arctanl∈L（m）＼ltanhvml2];

3） [x1]更新：[vml=v0l+m∈M（l）uml];

4） 似后验概率更新：[vl=v0l+m∈M（l）uml];

5） 比特判决：如果[vl>0]，则[xl=0]，否则，[xl=1（l=1，2，…，N）]。如果[HTx=0]或者迭代次数达到最大，则迭代终止，把[x]作为译码输出，否则转到步骤2）继续迭代。

LLR BP译码算法的基本译码步骤如图1所示。

图1  LLR BP译码算法流程图

2  基于相关性的LLR BP译码算法

2.1  相关性的介绍

[Xn，k]是经过编码后的发送信号，[Yn，k]是接收信号，[Nn，k]是均值为0，方差为[σ2]的高斯噪声，[H（n，k）]是编码的信道响应，[Yn，k]在频域内可以表示为：

[H（n，k）]会因[n]和[k]的变化而产生变化，当[n]变为[n+1]，或[k]变成[k+1]时，[H（n，k）]与[H（n+1，k）]，[H（n，k+1）]，[H（n+1，k+1）]之间存在一些相关性，在LLR BP译码算法里加入这些相关性可以降低变量节点外部信息震荡现象，译码就会更加准确。这种相关性同样在5G中也有可能得到应用[4]。

对二维[H（n，k）]的估计是固定[n]或[k]中的一个变量，这样就可以先估计一维[H（i）]。[H（n，k）]随[n]或[k]的变化而变化，但[H（n，k+1）]与[H（n，k）]是紧密联系着的。若[H（i）]位于频率方向，即[k]为下标，那么[H（n，k+1）]与[H（n，k）]总是近似。将相关性用[di]来表示，即相邻两个接收信号的比值和对应的发送信号的比值之差为[di=yi+1yi-xi+1xi]，[xi]是发送信号，[yi]是接收信号，推导得：

2.2  LLR BP译码改进算法

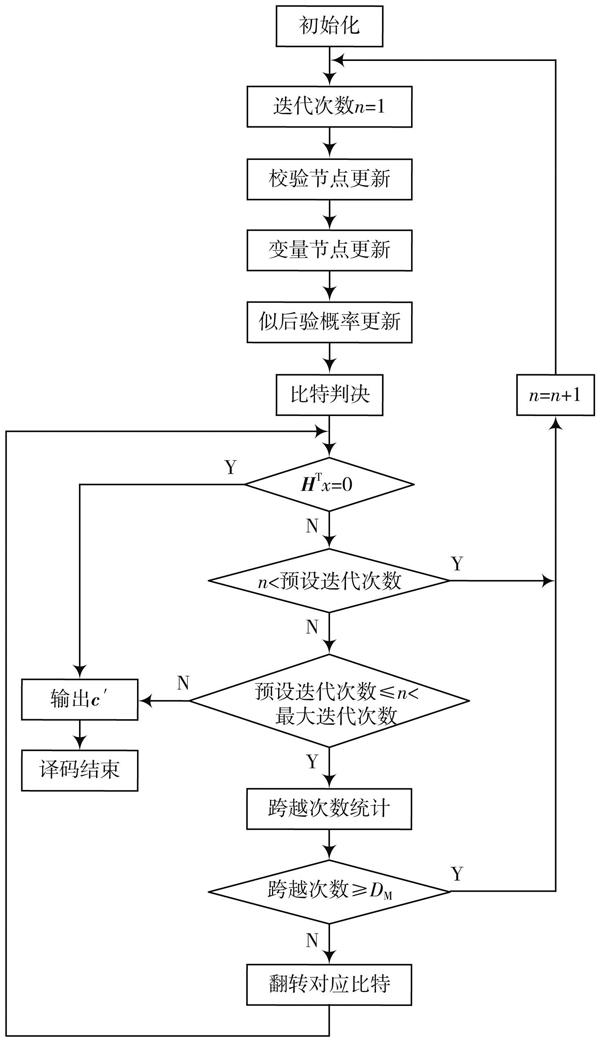
在译码前需要计算出小于给定的差错率[Ps（10-2）]的出错次数，记作[DM]，由[DM]来给定[de]的值。每个待翻转比特与其前后比特做对比，得出[di]值，若该比特的两个[di]值都大于[de]（即发生两次连续的跨越）[5]，则译码出错，要对该比特进行翻转。这样就可以对不稳定的比特进行翻转，同时在已翻转比特中再进行比较，如果再次出现跨越，则需要继续进行比特翻转，这样可以使得所有比特都满足条件。在这个改进的LLR BP译码迭代中[6]，软信息在[sm]和[xl]间不断地来回传递，最后得到正确的译码结果，操作流程见图2。与LLR BP译码算法相比，计算过程中只增加了对加入的响应相关性的计算，但通过增加相关性，就可以降低误码率和迭代次数，加快算法的收敛速度[7]。

图2中预设迭代次数需要设置的尽可能大。通过提前测出不能被正确译出的码字，并将其进行翻转[8]，这样可以使得得出正确译码的概率增大。

3  仿真过程

3.1  参数设置

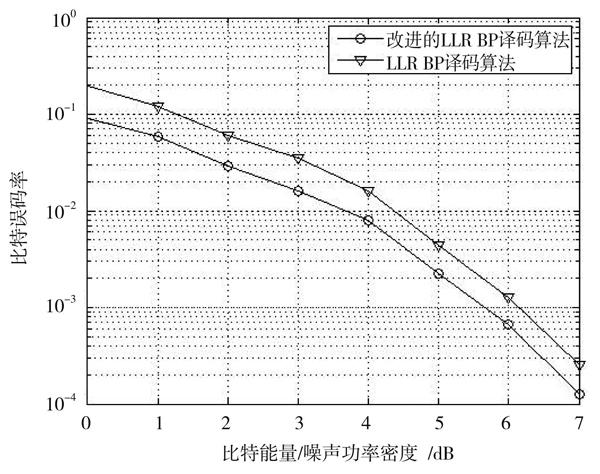
设校验因子为1，在允许迭代译码输出错误的条件下，进行8次连续迭代译码得到8个码字，与误码比特相比，输出码字的比特个数小于等于1，则连续译码次数为8次。仿真过程中，二进制LDPC码，其码长取值为504，码率为1/2，最大迭代次数设为30次，信噪比（Signal Noise Ratio，SNR）区间设为[-1.5，1.5] dB，步长[9]为0.5 dB。 采用Matlab对该算法进行仿真，并采用二进制相移键控进行调制，得到加入相关性改进后的译码算法和原始LLR BP译码算法的仿真对比图，如图3所示。

图2  加入相关性的LLR BP译码算法

图3  改进算法与LLR BP译码算法性能对比

3.2  结果分析

根据图3可以看出，基于相关性的LLR BP译码算法相较于LLR BP译码，相同信噪比下其误码率显著降低。

预设迭代次数是8次，当迭代次数大于8次时，系统会自动进入跨越，此时需要计算当前信噪比系统中的误码率来判断是否继续进行迭代，如果误码率小于[Ps]，则迭代终止。因此基于相关性的LLR BP译码算法中预设迭代次数是很重要的一个步骤[11]。通过仿真可以看出，基于相关性的LLR BP译码算法在只增加了响应相关性微小的计算量的情况下，在信噪比相同的条件下，大大降低迭代次数，并且降低误码率，使得译码性能有显著提升。

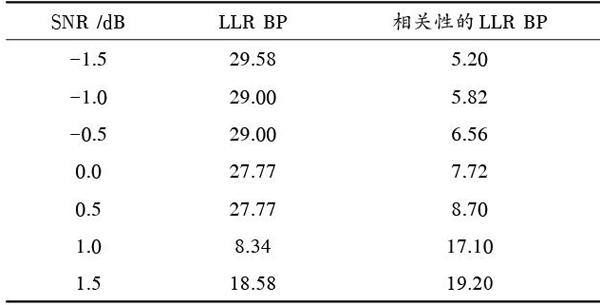
根据表1中两种译码算法的对比可以看出，当信噪比小于1.5 dB时，基于相关性的LLR BP译码算法可以很大地减小译码迭代的次数;当信噪比大于1.5 dB时，基于相关性的LLR BP译码算法迭代次数接近LLR BP算法迭代次数，这是因为在信噪比的值较高时不是依据检验因子是否处于稳定状態来确定输出结果是否正确[3，10]。

表1  两种译码算法的迭代次数对比

4  结  语

通过Matlab对基于相关性的LLR BP译码算法和传统LLR BP算法同时进行仿真，得出两种译码的对比图。由对比图很容易看出，与原始LLR BP译码算法相比，加入响应相关性的LLR BP译码算法在相同信噪比的条件下，迭代次数和误码率都有很大的降低，提高了译码效率。

参考文献

[1] 徐俊，许进，胡留军.一种应用于5G基于LDPC码的物理层包编码[J].中兴通讯技术，2016（3）：26?30.

XU Jun， XU Jin， HU Liujun. A physical layer packet coding based on LDPC codes for 5G [J]. ZTE communication technology， 2016（3）： 26?30.

[2] 贺鹤云.LDPC码基础与应用[M].北京：人民邮电出版社，2009.

HE Heyun. Basis and application of LDPC code [M]. Beijing： Posts and Telecom Press， 2009.

[3] 杜乐，郑娟毅，李永，等.一种适用于高速移动环境的LDPC译码算法[J].光通信研究，2017，43（4）：66?69.

DU Le， ZHENG Juanyi， LI Yong. A LDPC Decoding algorithm for the mobile environment of high speed [J]. Study on optical communications， 2017， 43（4）： 66?69.

[4] 洪银芳，李晖，王新梅.一种改进的Polar码的BP译码算法[J].西安电子科技大学学报，2016，43（4）：39?44.

HONG Yinfang， LI Hui， WANG Xinmei. Improved BP deco?ding algorithm for Polar codes [J]. Journal of Xidian University， 2016， 43（4）： 39?44.

[5] 姚顺铨，周武旸.一种新颖的TS?LDPC译码算法[J].计算机仿真，2008（4）：133?137.

YAO Shunquan， ZHOU Wuyang. A new decoding algorithm for TS?LDPC [J]. Computer simulation， 2008（4）： 133?137.

[6] CHEN P， CAI K， ZHENG S. Rate?adaptive protograph LDPC codes for Multi?Level?Cell （MLC） NAND FLASH memory [J]. IEEE communications letters， 2018， 22（6）： 1112?1115.

[7] SUN Z Y， LI H H. Improvement of LDPC codes decoding algorithm in the application of the rotational OFDM system [J]. Advanced materials research， 2014， 3190（934）： 111?118.

[8] YUAN J， LIU F， YE W， et al. A new coding scheme of QC?LDPC codes for optical transmission systems [J]. Optik?international journal for light and electron optics， 2014， 125（3）： 1016?1019.

[9] COTRONEI M， LAZZARO D， MONTEFUSCO L B， et al. Image compression through embedded multiwavelet transform co?ding [J]. IEEE transactions on image processing， 2000，9（2）：184?189.

[10] LI T， HUANG Q， WANG Z L， et al. Low?complexity enco?ding of binary quasi?cyclic codes based on Galois Fourier transform [C]// IEEE International Symposium on Information Theory. Istanbul： IEEE， 2013： 131?135.

[11] SONG H， CRUZ J R. Reduced?complexity decoding of Q?ary LDPC codes for magnetic recording [J]. IEEE transactions on magnetics， 2003， 39（2）： 1081?1087.

[12] 方承志，巩雪艳，刘洁.OFDM系统中基于响应相关性LDPC译码研究[J].计算机技术与发展，2016，26（8）：75?78.

FANG Chengzhi， GONG Xueyan， LIU Jie. Research on LDPC decoding based on response correlation in OFDM system [J]. Computer technology and development， 2016， 26（8）： 75?78.