Rasch模型在中学物理试卷分析中的应用

张华 周智良

摘   要：在当前的教育与心理测量中，Rasch模型分析強调对被试能力和试题难度水平的排序，具有客观等距的特征。文章利用高考物理成绩的分层抽样统计数据，根据Rasch模型的多项指标对高考试题进行了评价，分析了Rasch模型在中学物理试卷分析中的具体应用。研究表明，2018年的高考物理（全国Ⅱ）试题整体良好，强调了试题的基础性，但在以后的考试中，部分类型的题目仍需要适度调整。

关键词：Rasch模型;高考;试卷分析

中图分类号：G633.7 文献标识码：A     文章编号：1003-6148（2019）6-0068-4

1    引  言

在我国，高考对教育研究和教育教学的发展方向具有重要影响。各级教育部门、广大师生、家长及社会各界都特别关注高考试题的质量。目前，国内考试质量分析主要运用经典测量理论和项目反应理论。长期以来，经典测量理论被广泛运用于各级各类教育测量中，但在试题质量及成绩分析等方面，仍存在许多无法克服的技术问题，如在衡量试题的难易程度、分析考点分布，以及评价考生的能力水平是否被科学、客观、公平地测量等。针对以上问题，项目反应理论中的Rasch模型提供了一种新的分析方法。

1960年，丹麦数学家、教育学家G.Rasch提出了一种概率模型——Rasch模型，用来测量被试的潜在特质，它能够解决经典测量理论难以克服的两个典型问题：一是被试样本及测验试题依赖，二是被试能力与试题难度测量间的彼此干扰，从而使Rasch测量具有了客观等距的特征[1]。作为潜在特质的模型，Rasch 模型通过被试在题目上的作答来测量不可直接观察的潜在特质。

其基本原理如下：被试能力与该试题难度的函数表示特定被试对特定试题作出的特定反应的概率，且两者的差异决定了被试回答某一试题的正确与否。通过对数转换，Rasch 模型实现了在单维尺度上同时标度被试能力和试题难度水平，基于两者在单维度连续体上的位置，使试题与试题、试题与被试、被试与被试之间直接进行比较[2]。单维性假设是运用Rasch模型分析的条件，即单一变量影响了被试在某一项目上的表现，其他因素的影响可忽略不计。国内外大量研究表明，在分析试卷质量时，可以利用Rasch模型来检验和改进试卷[3]。本文以某市2018年物理高考试卷（全国Ⅱ）为例，探讨Rasch模型在试卷分析中的应用。

2    研究方法

2.1    研究样本

在某市2018年高考理科选考为选修3-3的考生中，采用分层抽样，抽取1078人。试卷包含选择题8个（含单选题5个和多选题3个），实验题2个，论述题2个，选做题1个，共计13个计分点。根据Rasch模型的要求，将试卷所有13个题目进行等级赋分，其中单选题为二级赋分，答对为1，答错为0;多选题为三级赋分，答对为2，答对部分为1，答错为0;同样的方法，实验题、计算论述题、选做题采用多级赋分。

2.2    研究工具与统计方法

运用SPSS22.0对收集到的原始数据进行清理和转化等预处理，进行单维性检验，所有测试数据以Excel格式和“记事本”格式输入。利用软件Winsteps3.72开展Rasch模型分析，分析结果包含整个试卷拟合情况、试卷中每个题目拟合情况、怀特图及气泡图分析。

3    结果与分析

3.1    测验的单维性检验

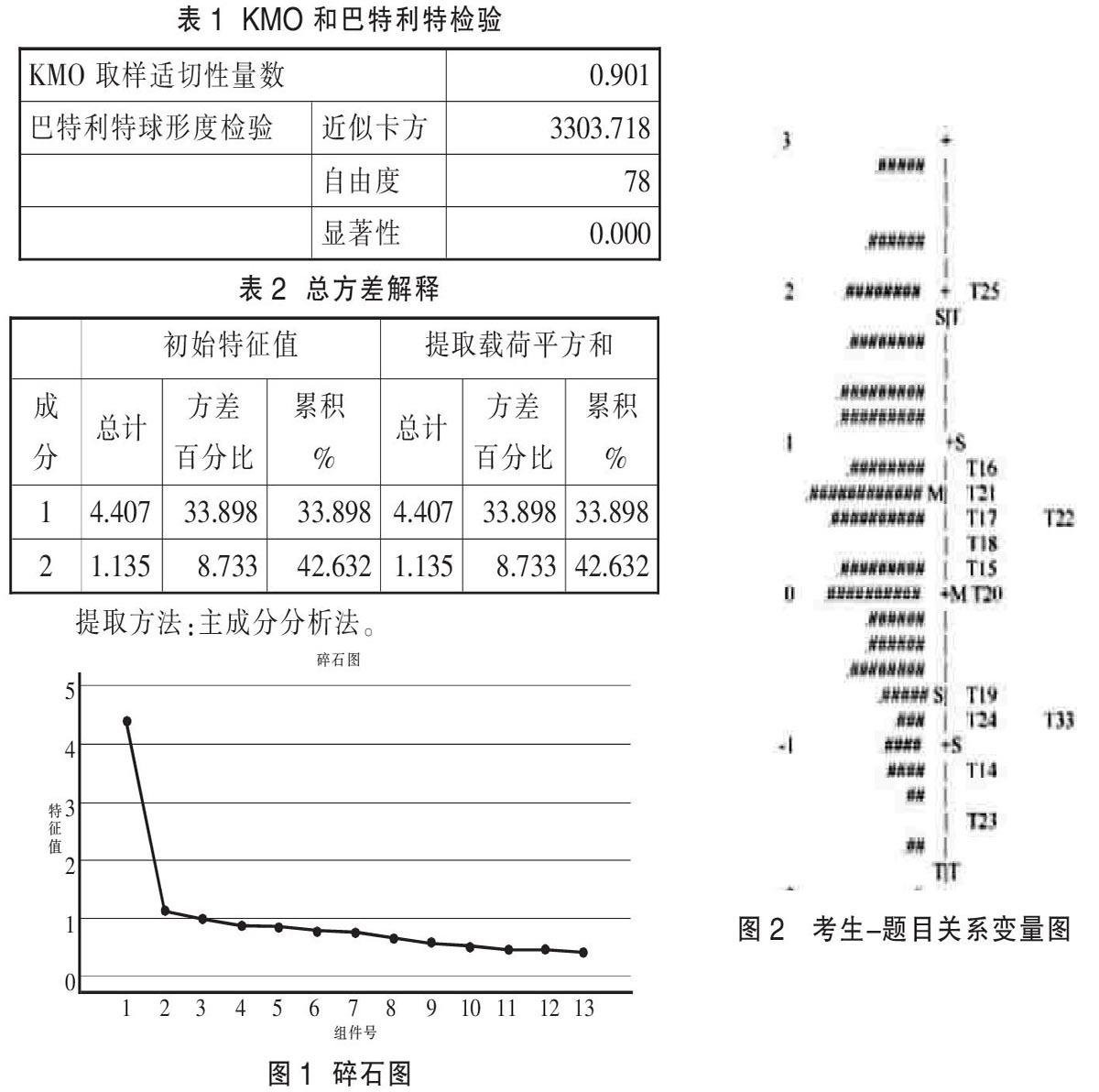
Rasch模型要求所测量的潜在特质具有单维性，即被试的作答表现只受其所掌握的物理知识影响，没有受到阅读理解能力等其他额外因素的影响。因此，在利用 WINSTEPS3.72进行参数估计之前，本研究运用SPSS22.0对高考数据进行探索性因素分析，统计显示（表1），KMO值为0.901（>0.7），Bartlett检验显著性为 P = 0（<0.05）[3]，符合探索性因素分析的条件。接下来开展因子分析（表2），采用主成分分析法提取特征根大于1的两个因子，其特征根分别为4.407和1.135;结合碎石图（图1），发现曲线在X轴1处出现明显的弯折，说明只有一个因子（所掌握的物理知识）影响了本次测验，符合Rasch模型单维性的条件。

情况

Infit和Outfit指标常被Rasch模型分析中用来判断数据与模型的拟合程度，Infit表示加权后的指标，Outfit表示未加权指标（易受极端值的影响）。Rasch模型常根据MNSQ和ZSTD（ZSTD是MNSQ的标准化形式）两个指标进行拟合度检验。MNSQ=1为理想拟合情况，其值在0.7～1.3之间，其拟合程度可被接受 [4]。当ZSTD=0时，数据与模型的拟合属于理想状态，当ZSTD取值介于-2～2之间时，认为拟合较好[5]。研究中还涉及到信度、区分度、难度、被试及试题分布等质量检验指标。Reliability表示信度，当其特征量大于0.70时，表示试卷测试结果的一致性、可靠性、稳定性较好。Separation表示区分度，当其特征量大于2时，表示试题具有较高的区分度。

统计显示，本试题和被试的MNSQ值均大于0.95，说明数据和模型拟合度良好;被试和项目的信度均高于0.8，说明测试结果稳定可靠;其Separation值为2.05，说明区分度合理。从试卷内容来看，强化了对基本物理概念、规律和实验技能等主干知识的考查。必考部分内容主要涵盖力学和电磁学，涉及匀变速直线运动、万有引力与航天、动量与机械能守恒、静电场、闭合电路欧姆定律、磁场和电磁感应等内容;选考部分则主要考查了气体实验定律、气体分子内能、光的折射、机械波等主要内容[6]。整个试卷突出考查了考生对物理学科基本概念、规律的理解及实验探究能力，具有良好的效度。

3.3    被试能力水平与试题难度水平分布關系图

在Rasch模型分析中，研究者通常利用怀特图了解测试工具中各项目的难度分布。怀特图能够在同一把标尺上，直观展示被试和被试、题目和题目、被试和题目之间的关系（图2）。

中线是 Logit 刻度尺，它是被试能力水平与试题难度水平进行比较的重要媒介。M代表平均水平（Mean）;S（One Standard Error）与M的距离为一个标准差（在标准正态分布中，占68.3%）;T（Two Standard Error）与均值的距离为两个标准差（在标准正态分布中，占95.4%）[7]。刻度尺左侧是被试的物理学习水平分布，每个 # 号代表7个被试，不够7用“.”表示，从下往上看，被试能力水平逐渐升高。刻度尺右侧是样本试卷中13道题目的分布情况。从下往上难度依次升高，有许多题目的难度水平较为接近。其中，实验题第23题最容易，论述题第25题难度最大。

在1078名考生中，考生能力平均值为0.68logit，考生能力水平高于试题难度，说明本次考试难度偏低。图2显示，被试能力水平分布范围约占7.4个logit，题目难度水平分布范围宽度约为3.6个logit。总体来看，被试能力水平范围跨度大于题目难度，题目难度没有覆盖到全体被试，特别是最高能力水平的考生。第19题和第20题、第16题和第25题之间都有比较大的空白区间，说明缺乏与被试能力相匹配的题目。

3.4    试卷中每个题目数据与Rasch模型的拟合度

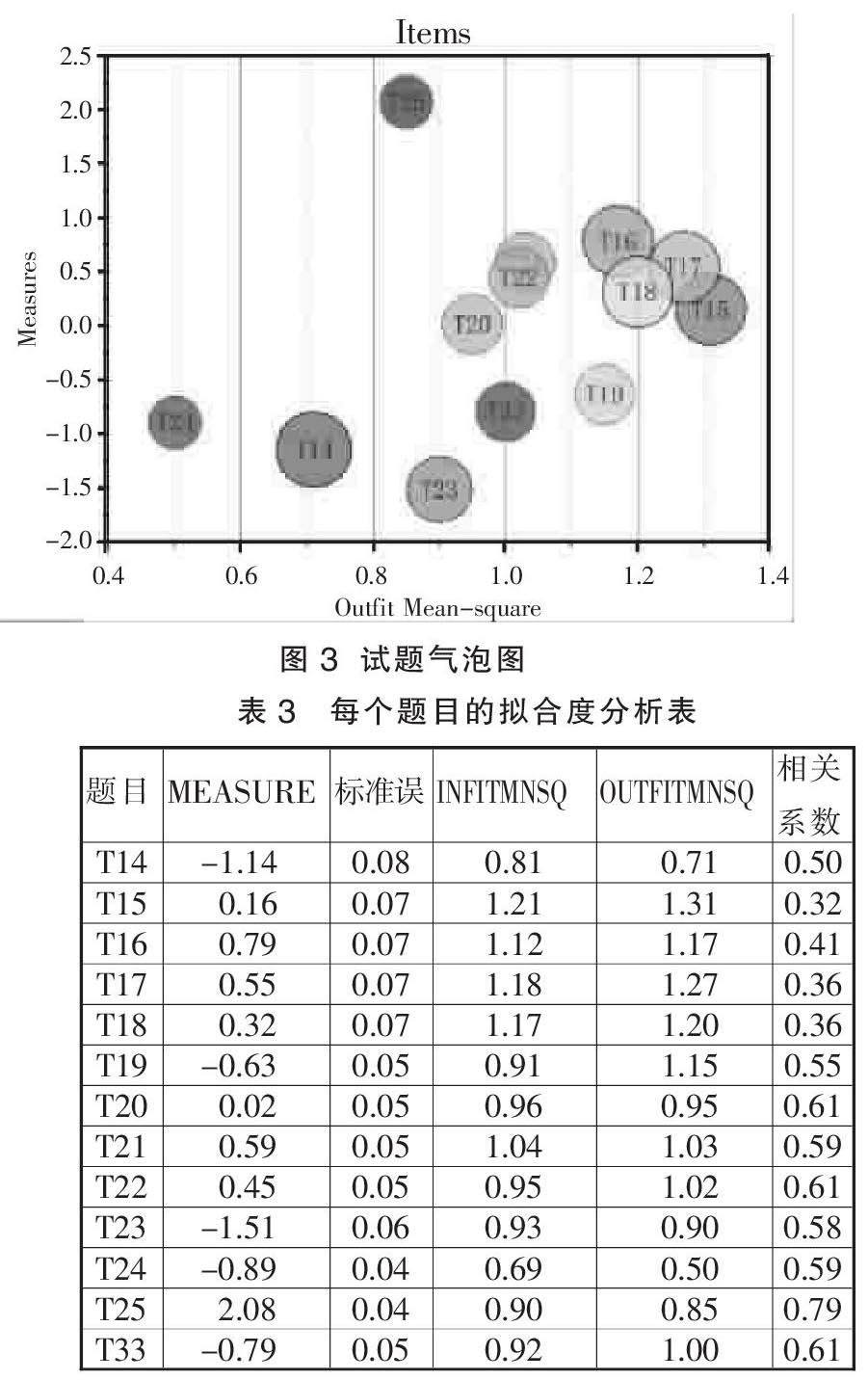
作为理想化的数学模型，Rasch模型要求搜集到的数据具备规定的标准和结构，才能实现客观等距的测量目标[8]。每个题目的测量数据与Rasch模型的拟合情况（表3），所有题目的Outfit MNSQ 范围均在0.50～1.31之间，Infit MNSQ范围在 0.69～1.21之间。除第24题以外，Infit MNSQ值（0.69）均在可接受的范围（0.7～1.3）以内，说明2018年高考物理数据与 Rasch 模型拟合较好。另外，利用Rasch模型测量考生能力水平时，其标准误主要表示测量的稳定性。标准误越小，说明试题对考生能力水平的估计越稳定，题目的信度也就越高。统计显示，所有题目的Rasch标准误均在0.08以下，说明试题的信度较高。此外，试题与试题测量目标的拟合程度由相关系数表示。0.30是可接受的相关系数最低水平，相关系数越高，试题就越接近测量目标。统计显示，所有题目的相关系数最小值为0.32，均处于可接受的范围内。

3.5    气泡图

图3横轴表示Outfit MNSQ，纵轴表示难度。气泡和题目一一对应，气泡的直径表示标准误的大小，气泡的位置表示试题的Outfit MNSQ值。图3显示，试题越靠近顶端，难度水平越大。研究显示，题目难度、拟合度及标准误等指标均可以用气泡图形象地描绘出来。所以在命制试题过程中，可运用气泡图来筛选试题。

在理想的气泡图中，所有气泡都会靠近中轴线 ，且不会有重叠。统计显示，除一个题目的 Outfit MNSQ值在0.7～1.3范围外（图3），其余大多数题目的数据与模型拟合较好。同时，发现有少部分气泡堆叠在一起，说明测验内容或题目的难度水平比较接近。第24题的 Intfit MNSQ值为0.69，Intfit MNSQ值为0.50，说明对被试能力水平的估计误差较大，应进一步探讨;第23题、第14题是较易的题目;第25题是较难的题目，而且第25题与其他试题明显分离，说明此题目与其他题目的难度水平差异较大。

4    结论与讨论

本研究运用Rasch模型，通过试题整体分析表、怀特图及气泡图对2018年某市高考物理成绩及试卷内容进行了分析，结果主要体现在以下两个面。

4.1    试卷突出了基础性

整体难度相对偏低，从试卷整体分析及怀特图可以看出，在本次测试中试题的难度水平没有覆盖到所有能力水平的考生，考生能力分布的logit值明显高于试题难度水平的 logit 值，二者相差3.8logit，试卷整体难度偏低。

比如第24题虽然是计算论述题，但难度仅排在第3。其背景为日常生活中较为常见的小型交通事故，考查被试对匀加速直线运动、牛顿运动定律和动量守恒定律等力学基本概念或规律的掌握程度。本题通过设置新颖的问题情境，将物理学主干知识与科学、技术、社会紧密联系起来，考查学生是否能够灵活运用物理知识和方法解决生活中的实际问题。

比如，实验题中，22题考查被试的基本实验能力和设计简单电路的能力。在直流电路部分欧姆定律是重要的规律，要求被试应用欧姆定律，根据实验目的改装电流表和电压表，利用所给器材设计实验电路，考查被试的基本实验探究能力。

4.2    个别题目需要适度调整

怀特图显示，试卷中的所有题目难度没有呈现出近似的正态分布，个别题目的难度、区分度需加强。

首先，试卷整体难度不平衡。在13个物理题目中，与被试零水平相对应的有一个题，表3显示了每个题目的measure数值，显示了题目的难度，数值越大，难度越高。分析发现，在13个题目中，1logit～2logit难度的题目处于空白状态;反而在0～1logit难度的题目多达7个。在以后的考试中，需要调整measure数值比较接近的题目，使之适当分散，使整个试题难度分布接近于正态分布。

其次，区分度仍需调整。理想拟合情况下的MNSQ值为1，当 Outfit MNSQ 和 Infit MNSQ 参数值大于 1 时，区分度翻转，即在作答该题时，许多高能力水平的被试对该题作答错误，而低能力水平的被试却回答正确;当小于0.7时，区分度趋同，即测试题目不能区分被试之间的能力水平，或者说被试的作答结果差异较小。按此依据，个别试题的拟合值存在一些问题。如第24题，其Outfit MNSQ值为0.50，说明了无论被试的能力水平高低，被试在本题的作答差异不大，没有体现出必要的区分度。

最后，难点的设置需进一步考量。在题目难点的布局上，一般都遵循先易后难的原则。但是在8个选择题中，第2个选择题（16题）却成为最难的选择题，而且在全卷13个题目中难度值排名第二，这在一定程度上会使被试产生不适应;同时，在实验题中，我们发现第23题，也就是后一个实验题，不仅比第一个实验题（22题）简单了1.96logit，而且是本试卷最简单的题目。按一般的命题规律，以上两题均偏离了命题的初衷。因此，在以后的考试中，可以根据考试大纲对此类试题进行适度调整或修改，使其充分发挥其高考的选拔功能。

综上所述，高考抽样数据分析在高考命题评价过程中具有重要作用。在一线教学中，为提高命题质量，可以在考试评价中引入项目反应理论及Rasch模型，将客观等距量尺引入到考试中来。这样，在各级各类考试中，首先指定命题规范，建立学科测评量表框架标准（比如双向细目表等），明确测试目标;然后运用先进的测量技术和数理统计方法，保证试卷对于不同群体考生的公平性，从而提高命题效率与质量。

参考文献：

[1]赵守盈，何妃霞，陈维，等. Rasch模型在研究生入学考试质量分析中的应用[J].教育研究，2012，389（6）：61-66.

[2]戴海琦.基于项目反应理论的测验编制方法研究[J].考试研究，2006（10）：31-44.

[3]王蕾. Rasch测量原理及在高考命题评价中的实证研究[J].中国考试，2008（1）：32-39.

[4]王桂桃，嚴文法，田秀云.例析Rasch模型在化学试卷质量分析中的应用[J].化学教学，2016（11）：14-19.

[5]教育部考试中心.聚焦主要内容 考查关键能力 凸显素养导向——2018年高考物理试题评析[J].中国考试，2018，315（7）：17-23.

[6]罗德红，龚婧.Rasch模型在试卷质量分析中的应用——基于五六年级学生阅读素养前测试卷的质量分析[J]. 教育测量与评价（理论版），2015（1）：18-22.

[7]袁洁.基于Rasch模型的大学英语分级考试质量分析[J].东南大学学报（哲学社会科学版）， 2016（6）：142-145.

（栏目编辑    张正严）